Introducción
En la entrada anterior vimos qué significa ser un conjunto y cuál es la notación que se utiliza para denotarlos. Además de un par de conceptos: pertenencia a un conjunto y subconjunto.
Retomaremos todo lo antes mencionado para ahora presentar las llamadas Operaciones con conjuntos. Éstas estarán presentes no sólo en este curso, sino también en varios de los textos de matemáticas que consultarás a lo largo de tu vida académica.
Operaciones con conjuntos
A lo largo de esta entrada haremos uso de una representación gráfica de los conjuntos llamada Diagramas de Venn para poder visualizar cada una de las operaciones que definiremos a continuación.
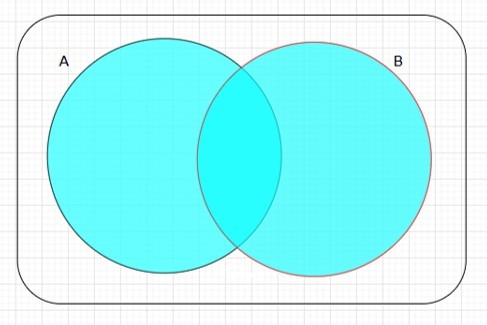
Definición (Unión): Sean $A$ y $B$ dos conjuntos. Decimos que la unión de $A$ con $B$ está definida como:
\[ A \cup B:=\left\{ x\mid x\in A \vee x\in B\right\} \text{.}\]
Esto quiere decir que está conformada por los elementos que se encuentran en $A$ o los que se encuentran en $B$. En el siguiente diagrama queda representada por la zona sombreada de azul.
Notación: Utilizamos el símbolo matemático $\vee$ para sustituir a la disyunción «o».
Observación. En este caso al hacer uso de la «o» estamos considerando que esta es inclusiva, lo que quiere decir que es válido que $x$ se encuentre tanto en $A$ como en $B$.
A continuación mostraremos un ejemplo para hacer más clara la definición.
Ejemplo: Supongamos que tenemos los siguientes conjuntos:
\[ A=\left\{0,1, 2, 3, 4\right\} \text{,}\]
\[ B=\left\{0, a,b,c,d,e\right\} \text{.}\]
Si nosotros queremos obtener $A \cup B$, al aplicar la definición anterior tenemos:
\[ A \cup B=\left\{0,1, 2, 3, 4,0,a,b,c,d,e \right\} \text{.} \]
Observamos que al realizar la unión de este par de conjuntos «unimos sus elementos en un sólo conjunto llamado $A \cup B$». Veamos que el 0 es un elemento tanto de $A$ como de $B$, por lo que sólo será necesario escribirlo una vez y así nos queda:
\[ A \cup B=\left\{0,1, 2, 3, 4,a,b,c,d,e \right\} \text{.}\]
Definición (Intersección): Sean $A$ y $B$ dos conjuntos. Decimos que la intersección de $A$ con $B$ está definida como:
\[ A \cap B:=\left\{ x\mid x\in A \wedge x\in B\right\} \text{.}\]
Esto quiere decir que está conformada por los elementos que se encuentran en $A$ y los que se encuentran en $B$. En otras palabras, la intersección está conformada por los elementos en común de $A$ y $B$.
Notación: Utilizamos el símbolo matemático $\wedge$ para sustituir a la conjunción «y».
En el diagrama anterior queda representada por la zona sombreada de verde.
Ejemplo: Retomamos los siguientes conjuntos:
\[ A=\left\{0,1, 2, 3, 4\right\} \text{,}\]
\[ B=\left\{0, a,b,c,d,e\right\} \text{.}\]
Si nosotros queremos obtener $A \cap B$, al aplicar la definición anterior tenemos:
\[ A \cap B=\left\{0 \right\}\text{.} \]
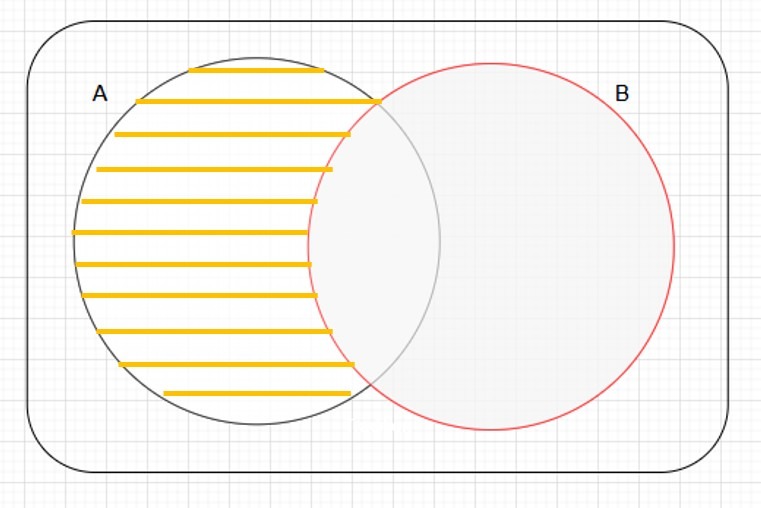
Definición (Diferencia): Sean $A$ y $B$ dos conjuntos. Decimos que la diferencia de $A$ con $B$ está definida como:
\[ A \setminus B:=\left\{ x\mid x\in A \wedge x\notin B\right\}\text{.} \]
Esto quiere decir que está conformada por los elementos que se encuentran en $A$ y que no se encuentran en $B$.
Ejemplo: Retomamos los conjuntos:
\[ A=\left\{0,1, 2, 3, 4\right\} \text{,}\]
\[ B=\left\{0, a,b,c,d,e\right\} \text{.}\]
Si nosotros queremos obtener $A \setminus B$, al aplicar la definición anterior tenemos:
\[ A \setminus B=\left\{1,2,3,4 \right\} \text{.}\]
Vemos que le hemos quitado los elementos a $A$ que tenía en común con $B$. Por lo que el diagrama nos quedaría como:
Teorema: Sean $A$, $B$ y $C$ conjuntos. Tenemos que:
- Propiedades conmutativas:
- \[A \cup B = B \cup A\quad \text{.}\]
- \[A \cap B = B \cap A\quad\text{.}\]
- Propiedades asociativas:
- \[A \cup (B\cup C) = (A \cup B)\cup C \quad \text{.}\]
- \[A \cap (B\cap C) = (A \cap B)\cap C \quad\text{.}\]
- Propiedades distributivas:
- \[A \cap (B\cup C) = (A \cap B)\cup (A\cap C)\quad\text{.}\]
- \[A \cup (B\cap C) = (A \cup B)\cap (A\cup C) \quad\text{.}\]
- \[ A\cup A= A \quad\text{.}\] \[A\cap A= A \quad\text{.}\]
- \[ A\subseteq A\cup B \quad\text{.} \] \[ A\cap B \subseteq A \quad\text{.}\]
- \[ A\cup \emptyset = A \quad\text{.}\] \[A\cap \emptyset= \emptyset\quad\text{.}\]
- Nota.-$\emptyset$ denota al conjunto vacío: es aquel que no posee elementos.
- \[A \setminus (B\cap C) = (A \setminus B)\cup (A\setminus C) \quad\text{.} \]
Demostración:
1.Probaremos la igualdad $A \cup B = B \cup A$, haciendo uso de la definición de igualdad de conjuntos, así tenemos:
$A \cup B = B \cup A$ si y sólo si $A\cup B\subseteq B \cup A$ y $B\cup A\subseteq A\cup B$
Comencemos con $A\cup B\subseteq B \cup A$. Sea $x\in A\cup B$, por la definición de subconjunto queremos probar que $x\in B\cup A$.
Por definición de unión se sigue que $x \in B$ o $x\in A$.
Caso 1: $x \in B$.
Como $x \in B$ entonces $x \in B$ o $x \in A$. Así, por la definición de unión concluimos que: $x\in B\cup A$.
Caso 2: $x \in A$.
Ahora como $x \in A$ entonces $x \in A$ o $x \in B$. Y como el conectivo «o» es conmutativo tenemos: $x \in A$ entonces $x \in B$ o $x \in A$. Así, por la definición de unión concluimos que: $x\in B\cup A$.
Del Caso 1 y Caso 2 concluimos que: $x\in B\cup A$. Por lo tanto, $A\cup B\subseteq B \cup A$.
Ahora probemos la segunda contención: $B\cup A\subseteq A\cup B$. Sea $x\in B\cup A$, así lo que queremos probar es $x\in A\cup B$.
Por definición de unión se sigue que $x \in B$ o $x\in A$.
Caso 3: $x \in B$.
Como $x \in B$ entonces $x \in B$ o $x \in A$, y como el conectivo «o» es conmutativo tenemos $x \in B$ entonces $x \in A$ o $x \in B$. Así, por la definición de unión concluimos que $x\in A\cup B$.
Caso 4: $x \in A$.
Ahora como $x \in A$ entonces $x \in A$ o $x \in B$. Así, por la definición de unión concluimos que $x\in A\cup B$.
Del Caso 3 y Caso 4 concluimos que: $x\in B\cup A$. Por lo tanto, $B\cup A\subseteq A\cup B$.
Por lo que finalmente probamos: $A\cup B = B \cup A$. La igualdad $A \cap B = B \cap A$ se dejará como ejercicio al lector.
2. Los incisos de las Propiedades asociativas quedan como ejercicio de Tarea moral.
3. Probaremos sólo la igualdad $A \cup (B\cap C) = (A \cup B)\cap (A\cup C)$.
Comenzaremos con probar la siguiente contención: $A \cup (B\cap C)\subseteq (A \cup B)\cap (A\cup C)$. Así tomemos $x\in A \cup (B\cap C)$, queremos demostrar que $x\in (A \cup B)\cap (A\cup C)$.
Caso 1: $x\in A$
Así tenemos que se cumple:
\begin{align}
x \in A\vee x\in B &\Rightarrow x\in A\cup B
\end{align}
Y también sucede que:
\begin{align}
x \in A\vee x\in C &\Rightarrow x\in A\cup C
\end{align}
En (1) y (2) aplicamos la propiedad de adición para la disyunción y la definición de la unión. Por lo que concluimos, al aplicar la definición de la intersección en (3):
\begin{align}
x\in A\cup B \wedge x\in A\cup C \Rightarrow x\in (A\cup B) \cap (A\cup C)
\end{align}
Caso 2: $x \in B\cap C$
Así por definición de intersección, tenemos que:
\begin{align}
x\in B \wedge x\in C &\Rightarrow (x\in B \wedge x\in C) \vee x\in A\\
&\Rightarrow (x\in B \vee x\in A) \wedge (x\in C \vee x \in A)\\
&\Rightarrow x\in B\cup A \wedge x\in C\cup A\\
&\Rightarrow x\in A\cup B \wedge x\in A\cup C\\
&\Rightarrow x\in (A\cup B) \cap (A\cup C)\\
\end{align}
Aplicamos en (4) la propiedad aditiva de la disyunción; para (5) usamos las Leyes distributivas de los conectivos disyunción y conjunción; para (6) y (7) aplicamos la unión y su propiedad conmutativa. Finalizamos aplicando en (8) la definición de intersección.
Por (3) y (8) de los Casos 1 y 2, podemos concluir que: $A \cup (B\cap C)\subseteq (A \cup B)\cap (A\cup C)$.
Ahora probaremos la contención: $(A \cup B)\cap (A\cup C)\subseteq A \cup (B\cap C)$.
Tomamos $ x\in (A \cup B)\cap (A\cup C)$. Así por definición de intersección, tenemos que:
\begin{align}
x\in (A \cup B) \wedge x \in (A\cup C) &\Rightarrow (x\in A \vee x\in B) \wedge (x \in A\vee x\in C)\\
&\Rightarrow x\in A \vee (x \in B \wedge x\in C)\\
&\Rightarrow x\in A \vee x \in B\cap C\\
&\Rightarrow x\in A \cup (B \cap C)
\end{align}
Vemos que (9) se sigue de la definición de unión. En (10) utilizamos las leyes distributivas de la disyunción con la conjunción; para (11) aplicamos la definición de intersección para $B$ y $C$.
Y por último en (12) aplicamos la definición de unión para $A$ y $B\cup C$.
Así concluimos que: $A \cup (B\cap C) = (A \cup B)\cap (A\cup C) \text{.}$
4. Tarea moral
5. Tarea moral
6. Tarea moral
7. Tarea moral
$\square$
Notación: El símbolo «$\Rightarrow$» se lee como «entonces».
Más adelante
Ahora que hemos terminado con el repaso de los conceptos básicos de Teoría de Conjuntos, en la siguiente entrada veremos el método de demostración llamado: Inducción matemática, el cuál será utilizado frecuentemente en los diferentes cursos a lo largo de tu preparación profesional.
Tarea moral
- Realiza la demostración de la siguiente Ley distributiva: $A \cap (B\cup C) = (A \cap B)\cup (A\cap C)$.
- Prueba que $A \setminus (B\cap C) = (A \setminus B)\cup (A\setminus C)$.
- Determina si las siguientes afirmaciones son verdaderas o falsas, argumenta tu respuesta:
- Si $x\in A$ y $A\subseteq B$, sucede que $x\in B$.
- Si $x\in A$ y $A\in B$, sucede que $x\in B$.
- Si tenemos $A$ y $B$ conjuntos, sucede siempre que $A\setminus B = B \setminus A$.
Entradas relacionadas
- Ir a: Cálculo Diferencial e Integral I
- Entrada anterior del curso: Cálculo Diferencial e Integral I: Introducción. Repaso: Teoría de Conjuntos (Parte 1)
- Entrada siguiente del curso: Cálculo Diferencial e Integral I: Repaso. Inducción matemática
- Álgebra Superior I: Propiedades de la negación, conjunción y disyunción
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»