Introducción
Ya que hemos revisado dos criterios importantes para determinar si un punto crítico de una función es un máximo o un mínimo, en esta entrada veremos que la obtención de los mismos tiene variadas aplicaciones prácticas.
En algunos problemas podría resultar fácil determinar la función que deseamos optimizar (maximizar o minimizar) ya que puede ser conocida previamente. Sin embargo, nos podemos enfrentar a casos más complicados donde no resulte inmediato obtenerla y expresarla en términos de una variable. Es por eso que damos las siguientes recomendaciones generales:
- Identifica la función de la cual se desea encontrar su máximo o su mínimo.
- En caso de que la función resulte ser de dos o más variables, observa los datos dados en el problema que te permitan expresarlas en función de una sola variable.
- Si el problema lo necesita, realiza una representación gráfica del planteamiento.
Problema 1
Encuentra dos números cuya suma sea $40$ y su producto sea máximo.
Solución:
Sabemos que:
\begin{equation}
x+y=40.
\end{equation}
Y lo que nos piden maximizar es el producto:
$$P=xy.$$
Para obtener la función a maximizar debemos poner a la variable $y$ en términos de $x$, por ello nos apoyaremos en la primera ecuación:
\begin{equation}
y=40-x.
\end{equation}
Sustituyendo lo anterior tenemos que la función a maximizar:
\begin{align*}
P(x)&=x(40-x)\\
&=40x-x^{2}\\
\therefore P(x)&=40x-x^{2}.
\end{align*}
Comencemos por buscar los valores críticos de la función, en consecuencia, derivamos una vez $P(x)$:
$$P'(x)=40-2x.$$
Ahora igualamos a cero la primera derivada:
\begin{align*}
P'(x)=0 &\Leftrightarrow 40-2x=0\\
&\Leftrightarrow 20-x=0\\
&\Leftrightarrow x=20
\end{align*}
Para obtener el máximo utilizaremos el Criterio de la primera derivada, así cuando:
Caso 1: $x<20$
\begin{align*}
P'(19)&= 40-2(19)\\
&=2 \tag{que es positivo}
\end{align*}
Caso 2: $x>20$
\begin{align*}
P'(21)&=40-2(21)\\
&=-2 \tag{que es negativo}
\end{align*}
Concluimos que $P$ tiene un máximo cuando $x=20$.
Para obtener el valor de $y$ sustituimos en $(2)$:
$$y=40-20 \Rightarrow y=20.$$
Por lo tanto los números buscados son $x=20$ y $y=20$.
Observamos que en el problema anterior no fue necesario realizar algún dibujo que nos facilitara su solución. En los siguientes problemas veremos que una representación gráfica puede ser de gran utilidad.
Problema 2
De los rectángulos con perímetro fijo, ¿Cuál tiene el área máxima?
Solución:
Consideremos a $P$ como el perímetro fijo y a $A$ el área del rectángulo, de lo anterior observamos:
\begin{align*}
A&=xy & P&=2x+2y
\end{align*}
Para obtener la función a maximizar despejamos del perímetro a la variable $y$:
\begin{align*}
P=2x+2y &\Rightarrow P-2x=2y\\
&\Rightarrow \frac{P}{2}-x=y
\end{align*}
Así la función sería:
\begin{align*}
f(x)&=x\left( \frac{P}{2}-x \right)\\
\therefore f(x)&= \frac{P}{2}x-x^{2}.
\end{align*}
Ahora buscaremos los puntos críticos de $f$ derivando una vez:
$$f'(x)=\frac{P}{2}-2x.$$
E igualando la derivada a cero:
\begin{align*}
f'(x)=0 &\Leftrightarrow \frac{P}{2}-2x =0\\
&\Leftrightarrow \frac{P}{2}=2x \\
&\Leftrightarrow \frac{P}{4}=x
\end{align*}
Para determinar que es máximo utilizaremos el Criterio de la segunda derivada, por lo que derivamos una segunda vez a la función:
$$f \dquote (x)=-2 < 0.$$
Por lo que $f$ tiene un máximo cuando $x=\frac{P}{4}$.
Obtenemos el valor de $y$ sustituyendo $x=\frac{P}{4}$:
\begin{align*}
y&=\frac{P}{2}-\frac{P}{4}\\
&=\frac{P}{4}
\end{align*}
Concluimos que el rectángulo buscado es aquel que tiene lados $x=\frac{P}{4}$ y $y=\frac{P}{4}$.
Problema 3
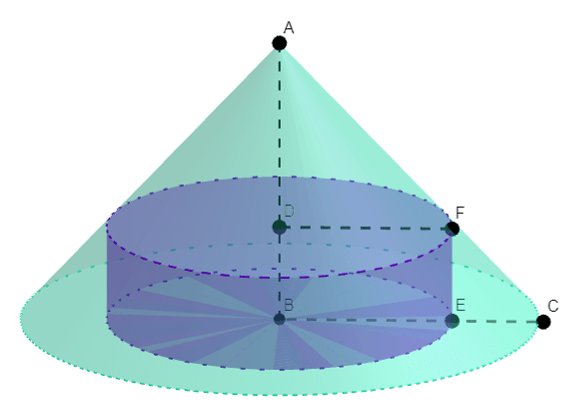
Calcular el radio y la altura de los cilindros de volumen máximo y mínimo que puedan inscribirse en un cono con un radio de $6 cm$ y $12 cm$ de altura. En la siguiente imagen podemos ver más claro el planteamiento anterior:
Solución:
Tenemos que el radio está dado por $BC$ y que la altura por $AB$:
\begin{align*}
BC&= 6 & AB&=12
\end{align*}
Además el volumen de un cilindro está dado por la ecuación:
$$V=\pi x^{2}y.$$
donde $x$ es el radio y $y$ la altura.
Lo que queremos calcular es:
\begin{align*}
BE&=x & BD&=y
\end{align*}
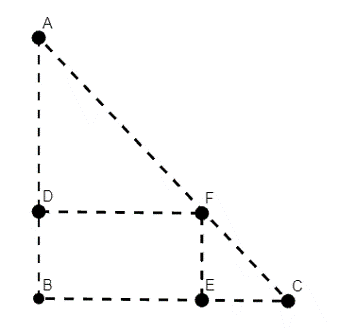
Observemos que de la imagen anterior tenemos
de donde el triángulo formado por los puntos $A, B, C$ es semejante con el triángulo formado por $F,E,C$:
$$\triangle ABC \sim \triangle FEC.$$
Por lo que tenemos la siguiente igualdad:
$$\frac{BC}{EC}=\frac{AB}{FE}.$$
Sustituimos $BC=6$ y $AB =12$:
$$\frac{6}{EC}=\frac{12}{FE}.$$
Además, como tenemos que para $EC$ se cumple la igualdad:
\begin{align*}
EC&=BC-BE\\
&=6 -x \tag{por $BE=x$}
\end{align*}
Por lo anterior y recordando que $y=FE$ se sigue:
$$ \frac{6}{6-x}=\frac{12}{y}.$$
Despejando a $y$ de la igualdad anterior:
\begin{align*}
\frac{6}{6-x}=\frac{12}{y} &\Leftrightarrow \frac{6y}{6-x}=12\\
&\Leftrightarrow 6y = 12(6-x)\\
&\Leftrightarrow y=\frac{72-12x}{6}\\
&\Leftrightarrow y = 12-2x
\end{align*}
Obtenemos la función a maximizar sustituyendo $y=12-2x$ en $V=\pi x^{2}y$:
\begin{align*}
V(x)&=\pi x^{2}(12-2x )\\
&=12\pi x^{2}-2\pi x^{3}
\end{align*}
Derivemos $V(x)$:
$$V'(x)=24\pi x -6\pi x^{2}.$$
Igualemos a cero para obtener los valores críticos:
\begin{align*}
V'(x)=0 &\Leftrightarrow 24\pi x -6\pi x^{2}=0\\
&\Leftrightarrow 4x-x^{2} \tag{dividimos entre $6\pi$}\\
&\Leftrightarrow x(4-x)=0\\
&\Leftrightarrow x=0 \quad \text{o}\quad x=4
\end{align*}
Determinaremos si se trata de un máximo o un mínimo utilizaremos el Criterio de la segunda derivada considerando:
$$V \dquote (x)=24\pi-12\pi x.$$
Veamos para $x=0$:
$$V \dquote (0)=24 \pi > 0,$$
por lo que en consecuencia $V$ tiene un mínimo.
Ahora para $x=4$:
$$V \dquote (4)=-24\pi <0,$$
por lo tanto $V$ tiene un máximo.
Para obtener las dimensiones recordemos que:
$$y=12-2x.$$
Cilindro con volumen mínimo
$$x=0 \quad \text{y} \quad y=12-2(0)=12$$
Cilindro con volumen máximo
$$x=4 \quad\text{y}\quad y=12-2(4)=4$$
Problema 4
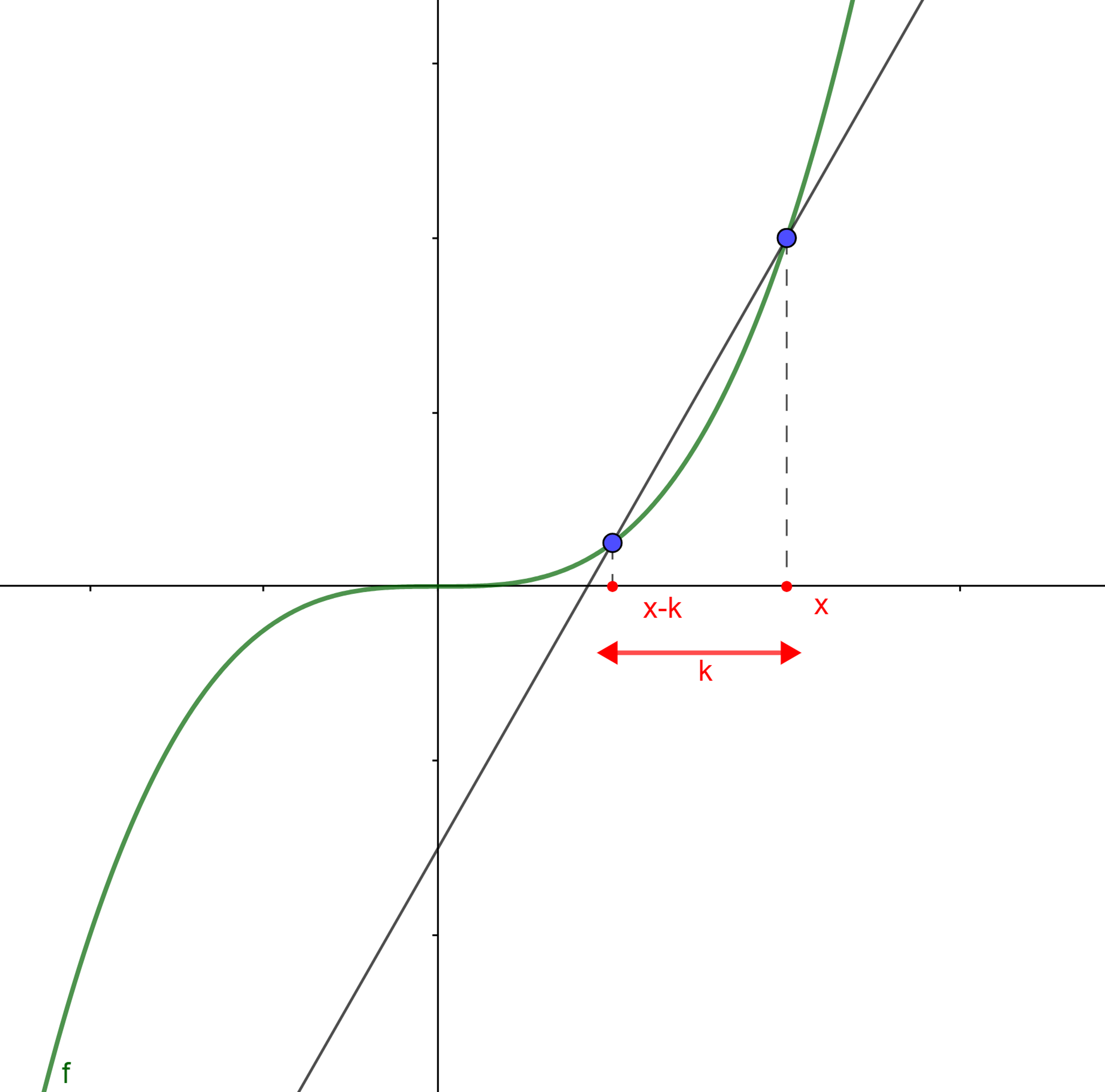
Hallar los puntos sobre la gráfica de la función $f(x)=x^{3}$ cuyas abscisas difieren en $k$ unidades tal que la recta que los une tenga pendiente mínima:
Solución:
La pendiente de la recta que une el par de puntos de la imagen está dada por:
\begin{align*}
m&=\frac{(x-k)^{3}-x^{3}}{(x-k)-x}.\\
\end{align*}
Ahora simplificando lo anterior obtenemos la función a minimizar:
$$m(x)=3x^{2}-3kx+k^{2}.$$
Derivamos e igualamos a cero:
$$m'(x)=6x-3k \Rightarrow 6x-3k=0$$
Por lo que veamos si cuando $x=\frac{k}{2}$ se trata de un mínimo usando el Criterio de la segunda derivada:
$$m\dquote (x)=6 >0.$$
Concluimos que $m$ tiene un mínimo cuando $x=\frac{k}{2}$ y hallamos los puntos sustituyendo en $f(x)=x^{3}$:
$$f\left(\frac{k}{2}\right)=\left(\frac{k}{2}\right)^{3}=\frac{k^{3}}{8}.$$
Por lo que los puntos que cumplen son de la forma:
$$\left(\frac{k}{2},\frac{k^{3}}{8}\right).$$
A continuación, te presentamos una lista de ejercicios que te permitirán reforzar lo visto en esta entrada, verás que algunos de ellos tienen planteamientos similares.
Más adelante
Ya que hemos revisado algunos problemas que involucran obtener el máximo o mínimo de una función en distintos planteamientos, en la próxima entrada veremos problemas relacionados con los temas de velocidad y aceleración donde igualmente el uso de la derivada será fundamental para su solución.
Tarea moral
- Obtener dos números cuyo producto sea $16$ y cuya suma sea mínima.
- Hallar las dimensiones del rectángulo con perímetro de $72$ unidades y de área máxima.
- Obtener las coordenadas del punto $A$ sobre la curva $f(x)=x^{2}$ más cercano al punto $B=(3,0)$.
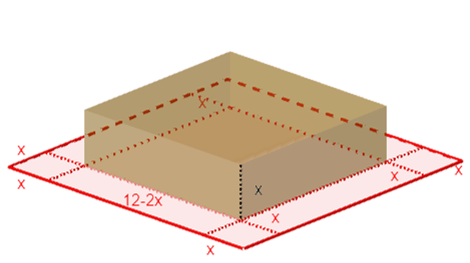
- Utilizando un cartón de forma cuadrada de 12 cm de lado se desea construir una caja abierta recortando cuadrados iguales de las esquinas y doblando hacia arriba. Por lo que se te pide determinar la longitud del lado $x$ de los cuadrados de las esquinas para que la caja:
- Tenga volumen máximo
- Tenga volumen mínimo
Entradas relacionadas
- Ir a: Cálculo Diferencial e Integral I
- Entrada anterior del curso: Cálculo Diferencial e Integral I: Localización de máximos y mínimos. Regiones de convexidad y puntos de inflexión.
- Entrada siguiente del curso: Cálculo Diferencial e Integral I: Velocidad y aceleración.
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

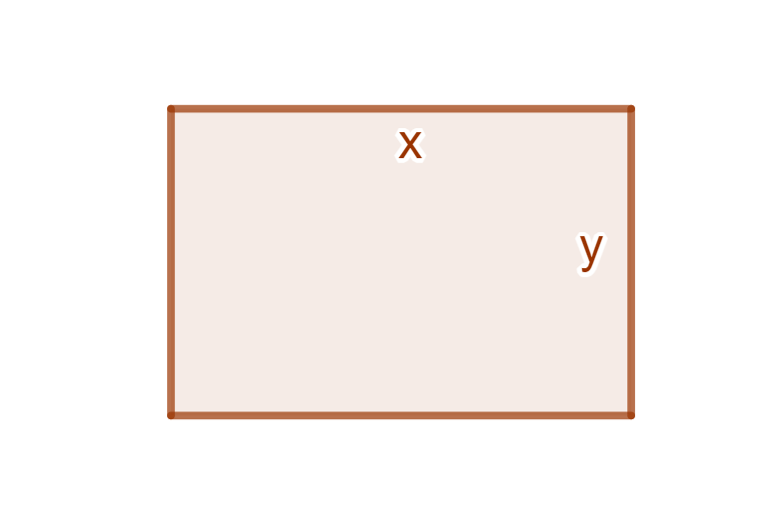
Hola estimado Leo, como puedo acceder al NEKOMATH LEARN ? no hay para registrarse y acceder so estudiante de matemáticas e informática en Perú , por favor , gracias, saludos.
Hola Joaquin. Lo que tenemos en NekoMath Learn lo estamos migrando poco a poco a Matemáticas a Distancia, en donde el material es accesible libremente, sin tener una cuenta. Por el momento mi recomendación es que entres a esa página, que es actualmente trabajo en progreso: https://www.mdistancia.com.