Introducción

En las entradas anteriores hemos trabajado con la definición de límite y revisamos sus propiedades. En esta ocasión, daremos la definición de límite por la derecha y límite por la izquierda, que en conjunto son llamados límites laterales. De igual forma, revisaremos algunos ejemplos y su relación con la definición vista anteriormente.

Límites laterales

Las definiciones que veremos a continuación se basan en restringir la forma en que nos acercamos a $x_0.$ El límite por la derecha se enfoca en acercarnos por la derecha, es decir, pediremos que $x > x_0,$ lo cual se traducirá en que debe cumplirse que $0<x-x_0 < \delta$. Por otro lado, para el límite por la izquierda debe cumplirse que $x < x_0,$ de esta forma se tendrá que $0<x_0-x< \delta.$ Primero daremos la definición de límite por la derecha.

Definición. Sean $A \subset \mathbb{R}$ y $f: A \rightarrow \mathbb{R}.$ Se dice que $L \in \mathbb{R}$ es límite por la derecha de $f$ en $x_0,$ si para todo $\varepsilon >0$ existe $\delta > 0$ tal que si $0<x-x_0<\delta$ entonces $|f(x)-L| < \varepsilon.$ Cuando $L$ es el límite de $f$ en el punto $x_0$ por la derecha, lo denotamos $$\lim_{x \to x_0+} f(x) = L.$$

Análogamente, tenemos la definición de límite por la izquierda.

Definición. Sean $A \subset \mathbb{R}$ y $f: A \rightarrow \mathbb{R}.$ Se dice que $L \in \mathbb{R}$ es límite por la izquierda de $f$ en $x_0,$ si para todo $\varepsilon >0$ existe $\delta > 0$ tal que si $0<x_0 – x<\delta$ entonces $|f(x)-L| < \varepsilon.$ Cuando $L$ es el límite de $f$ en el punto $x_0$ por la izquierda, lo denotamos $$\lim_{x \to x_0-} f(x) = L.$$

Propiedades de los límites laterales

De forma similar al teorema que vimos para los límites, existe una relación entre el límite lateral de una función y el límite de una sucesión, basta agregar a los supuestos la condición de que la sucesión sea mayor que $x_0$ para todo $n \in \mathbb{N}$ en el caso de límite por la derecha y que sea menor que $x_0$ para todo $n \in \mathbb{N}$ en el caso de límite por la izquierda.

Teorema. Sea $A \subset \mathbb{R}.$ Definimos la función $f:A \rightarrow \mathbb{R}.$ Entonces, dado un $x_0,$ los siguientes enunciados son equivalentes.

1. $$\lim_{x \to x_0+} f(x) = L.$$
2. Para toda sucesión $\{ a_n \}$ en $A$ que converge a $x_0$ y tal que $a_n > x_0$ para todo $n\in \mathbb{N},$ la sucesión $\{f(a_n)\}$ converge a $L.$

El teorema de límite por la izquierda es similar al anterior. Además, la demostración es totalmente análoga a la revisada en una entrada anterior por lo cual quedará como tarea moral. También recordemos que este teorema nos ayuda a determinar las propiedades que tienen los límites laterales debido a la herencia que nos brinda el límite de una sucesión; es gracias a ello que podremos hacer uso de tales propiedades en los siguientes ejemplos.

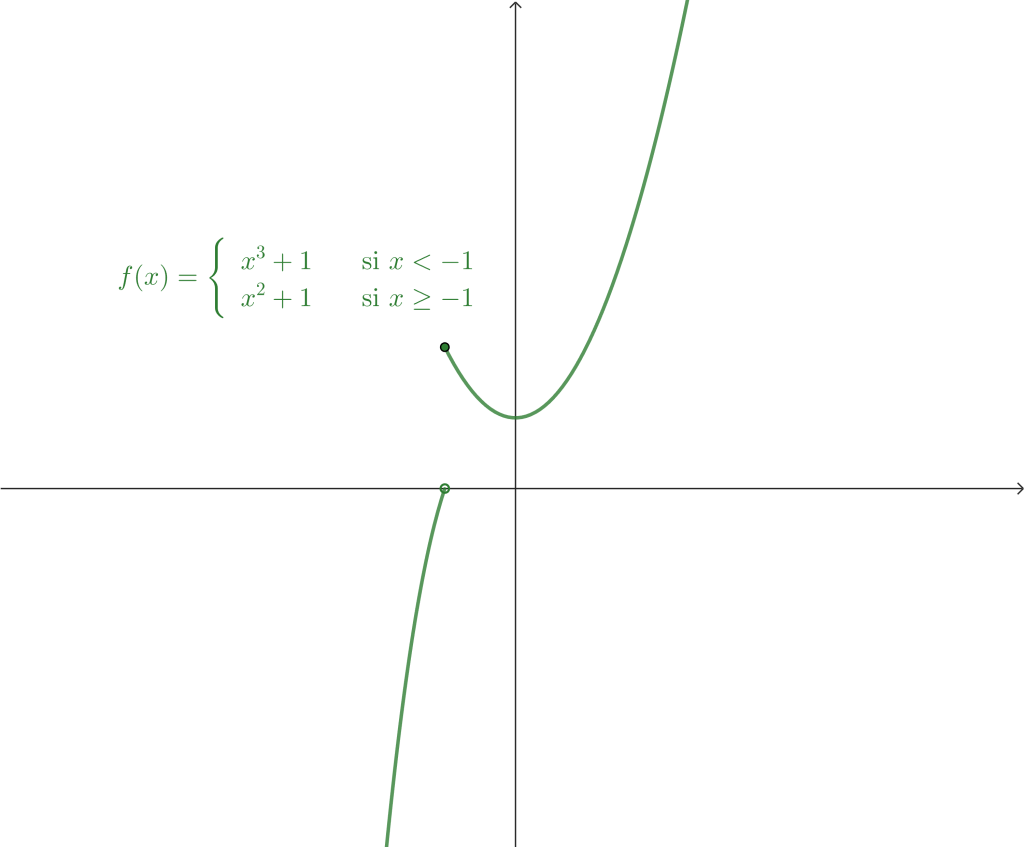
Ejemplo 1. Sea $f: \mathbb{R} \rightarrow \mathbb{R},$ definida de la siguiente forma

$$f(x) =
\begin{cases}
x^3+1 & \quad \text{si } x<-1 \\
x^2+1& \quad \text{si } x \geq -1. \\
\end{cases}
$$

Determina los límites laterales en $x_0 = -1.$

Primero mostraremos la gráfica de la función:

Calculando el límite por la izquierda, tenemos
$$\lim_{x \to -1^-} f(x) = \lim_{x \to -1^-} x^3+1 = 0.$$

Por otro lado, el límite por la derecha
$$\lim_{x \to -1^+} f(x) = \lim_{x \to -1^+} x^2+1= 2.$$

Por lo tanto
$$\lim_{x \to 0^-} f(x) = 0 \quad \text{ y } \quad \lim_{x \to 0^+} f(x) = 2.$$

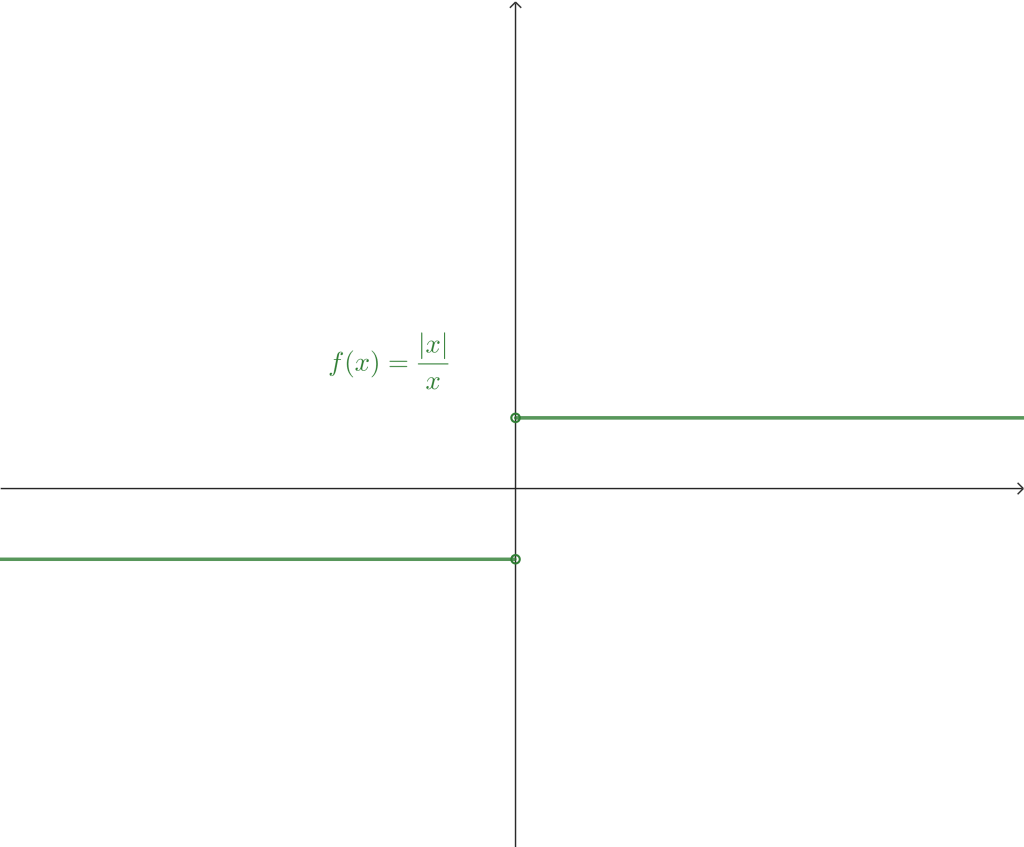
Ejemplo 2. Sea $f: \mathbb{R} \setminus \{0 \} \rightarrow \mathbb{R}.$ Calcula los límites laterales en $x_0 = 0$ de

$$f(x) = \frac{|x|}{x}.$$

La gráfica de la función es la siguiente:

Calculando el límite por la izquierda, tenemos
\begin{align*}
\lim_{x \to 0^-} f(x) = & \lim_{x \to 0^-} \frac{|x|}{x} \\
= & \lim_{x \to 0^-} \frac{-x}{x} \text{, pues $x$ < 0} \\
= & \lim_{x \to 0^-} -1 \\
= & -1.
\end{align*}
Por otro lado, el límite por la derecha
\begin{align*}
\lim_{x \to 0^+} f(x) = & \lim_{x \to 0^+} \frac{|x|}{x} \\
= & \lim_{x \to 0^+} \frac{x}{x} \text{, pues $x$ > 0} \\
= & \lim_{x \to 0^+} 1 \\
= & 1.
\end{align*}
Por lo tanto
$$\lim_{x \to 0^-} f(x) = -1 \quad \text{ y } \quad \lim_{x \to 0^+} f(x) = 1.$$

De los ejemplos revisados, el primero tiene la propiedad de que sus límites laterales son iguales mientras que para el segundo y el tercero tales límites son distintos en $x_0.$

Relación entre el límite de una función y sus límites laterales

Parece inmediato inferir que, considerando un punto $x_0$ dado, si los límites por la izquierda y por la derecha existen y son iguales, entonces el límite de la función sí existe en tal punto. De la misma manera, resulta natural que si el límite existe, entonces los límites laterales también existen y son iguales. Probaremos esta equivalencia, pero para hacerlo, primero demostraremos la siguiente proposición.

Proposición. Sean $x,$ $x_0$ en $\mathbb{R}$ y $\delta >0.$ Entonces $0<|x-x_0|< \delta$ si y solo si $0<x-x_0<\delta \quad$ ó $\quad 0<x_0-x<\delta.$

Demostración.
Supongamos que $0<|x-x_0|< \delta$.

Caso 1: $x-x_0 > 0$.
Entonces $|x-x_0| = x-x_0$, así
\begin{gather*}
0<|x-x_0|< \delta \Leftrightarrow 0< x-x_0 < \delta.
\end{gather*}

Caso 2: $x- x_0 < 0$.
Entonces $|x-x_0| = x_0-x$, así
\begin{gather*}
0<|x-x_0| < \delta \Leftrightarrow 0< x_0-x < \delta.
\end{gather*}

$$\therefore 0<|x-x_0|< \delta \Leftrightarrow 0<x-x_0<\delta \quad \text{ ó } \quad 0<x_0-x<\delta.$$

$\square$

Teorema. El límite de una función $f$ en el punto $x_0$ existe y es igual a $L$ si y solo si los límites laterales existen y son iguales a $L$, es decir

$$\lim_{x \to x_0} f(x) = L \quad \Leftrightarrow \quad \lim_{x \to x_0^+} f(x) = L = \lim_{x \to x_0^-} f(x).$$

Demostración.

$\Rightarrow]$ Supongamos que $$\lim_{x \to x_0} f(x) = L.$$
Sea $\varepsilon > 0$. Como $f$ converge a $L$ en $x_0$, existe $\delta > 0$ tal que si $0<|x-x_0|< \delta$ se tiene que $|f(x)-L| < \varepsilon.$

Si $0<x-x_0 < \delta$, entonces $0<|x-x_0|< \delta$ por la proposición anterior. Se sigue que
\begin{gather*}
|f(x)-L| < \varepsilon. \\
\therefore \lim_{x \to x_0^+} f(x) = L.
\end{gather*}

Si $0<x_0-x < \delta$, entonces $0<|x-x_0|< \delta$ por la proposición anterior. Se sigue que
\begin{gather*}
|f(x)-L| < \varepsilon. \\
\therefore \lim_{x \to x_0^-} f(x) = L.
\end{gather*}

$\Leftarrow]$ Supongamos que $$\lim_{x \to x_0^+} f(x) = L = \lim_{x \to x_0^-} f(x)$$
Sea $\varepsilon > 0.$

Como $\lim\limits_{x \to x_0^+} f(x) = L$, existe $\delta_1$ tal que si $0<x-x_0<\delta_1$ entonces $|f(x)-L| < \varepsilon.$

Como $\lim\limits_{x \to x_0^-} f(x) = L$, existe $\delta_2$ tal que si $0<x_0-x<\delta_2$ entonces $|f(x)-L| < \varepsilon.$

Consideremos $\delta = min \{ \delta_1, \delta_2\}.$ Por la proposición, si $0<|x-x_0|< \delta$, entonces $0<x-x_0<\delta$ ó $0<x_0-x<\delta.$

Para el primer caso, tenemos que $0<x-x_0<\delta \leq \delta_1$, entonces $|f(x)-L| < \varepsilon.$
Para el segundo caso, se tiene que $0<x_0-x<\delta \leq \delta_2$, entonces $|f(x)-L| < \varepsilon.$

Por lo tanto $$\lim_{x \to x_0} f(x) = L.$$

$$\therefore \lim_{x \to x_0} f(x) = L \quad \Leftrightarrow \quad \lim_{x \to x_0^+} f(x) = L = \lim_{x \to x_0^-} f(x).$$

$\square$

Observación. Ya que hemos demostrado este teorema, podemos notar que si los límites laterales de una función son distintos en un punto $x_0$, entonces no existe el límite de la función en tal punto.

Finalizaremos esta entrada revisando los siguientes ejemplos.

Ejemplo 3. Determina si existe el límite en $x_0 = 0$ para la siguiente función $$f(x) = x \sqrt{\frac{1}{4x^2}-16}.$$

Veamos primero qué sucede con el límite por la izquierda
\begin{align*}
\lim_{x \to 0^-} f(x) = & \lim_{x \to 0^-} x \sqrt{\frac{1}{4x^2}-16} \\ \\
= & \lim_{x \to 0^-} x \sqrt{\frac{1-64x^2}{4x^2}} \\ \\
= & \lim_{x \to 0^-} \frac{ x \sqrt{1-64x^2} }{ \sqrt{4x^2} } \\ \\
= & \lim_{x \to 0^-} \frac{ x \sqrt{1-64x^2} }{ 2|x|} \\ \\
= & \lim_{x \to 0^-} \frac{ x \sqrt{1-64x^2} }{ -2x} \text{, pues $x$ < 0} \\ \\
= & \lim_{x \to 0^-} – \frac{\sqrt{1-64x^2} }{2} \\ \\
= & – \frac{1}{2}.
\end{align*}

De forma similar, tenemos que
\begin{align*}
\lim_{x \to 0^+} f(x) = & \lim_{x \to 0^+} x \sqrt{\frac{1}{4x^2}-16} \\ \\
= & \lim_{x \to 0^+} x \sqrt{\frac{1-64x^2}{4x^2}} \\ \\
= & \lim_{x \to 0^+} \frac{ x \sqrt{1-64x^2} }{ 2x} \text{, pues $x$ > 0} \\ \\
= & \lim_{x \to 0^+} \frac{\sqrt{1-64x^2} }{2} \\ \\
= & \frac{1}{2}.
\end{align*}
$$\therefore \lim_{x \to 0^-} f(x) = -\frac{1}{2} \quad \text{ y } \quad \lim_{x \to 0^+} f(x) = \frac{1}{2}.$$

Como los límites laterales son distintos, podemos concluir que el límite de la función $f$ no existe en el punto $x_0 = 0.$

Ejemplo 4. Sea $f: \mathbb{R} \rightarrow \mathbb{R}$, definida de la siguiente forma
$$f(x) =
\begin{cases}
x^2 & \quad \text{si } x<5 \\
2x+15 & \quad \text{si } x \geq 5. \\
\end{cases}
$$
Determina si el límite existe en $x_0 = 5.$

Iniciemos calculando el límite por la izquierda.
$$\lim_{x \to 5^-} f(x) = \lim_{x \to 5^-} x^2 = 25.$$

Por otro lado, el límite por la derecha
$$\lim_{x \to 5^+} f(x) = \lim_{x \to 5^+} 2x+15 = 25.$$

Por lo tanto
$$\lim_{x \to 0^-} f(x) = 25 \quad \text{ y } \quad \lim_{x \to 0^+} f(x) = 25.$$

Como los límites laterales existen y son iguales, podemos concluir que
$$\lim_{x \to 0} f(x) = 25.$$

Más adelante…

¿Qué sucede cuando en lugar de acercarnos a un punto en particular $x_0$, hacemos que $x$ crezca indefinidamente? Esto y otras ampliaciones del concepto del límite serán revisadas en la siguiente entrada con lo cual estaremos listos para calcular todo tipo de límites y, con ello, podremos conocer el comportamiento que toman las funciones tanto en un punto específico como «en el infinito».

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

• Demuestra que
  $i$) $\lim_\limits{x \to 0^+} f(x) = \lim_\limits{x \to 0^-} f(-x).$
  $ii$) $\lim_\limits{x \to 0} f(|x|) = \lim_\limits{x \to 0^+} f(x).$
• Usando la definición épsilon-delta de límite por la derecha, prueba que $\lim_{x \to 8^+} \sqrt{x-8} = 0.$
• Calcula el límite en $x_0 = 5$ de la función
  $$f(x) =
  \begin{cases}
  \frac{x^2-12x+35}{x-5} & \quad \text{si } x < 5 \\
  \frac{x-5}{1- \sqrt{x-4} } & \quad \text{si } x \geq 5.
  \end{cases}
  $$
• Usando límites laterales, determina si existe $$\lim_{x \to 0} \frac{3x + |x|}{7x-5|x|}.$$

Entradas relacionadas

• Ir a Cálculo Diferencial e Integral I
• Entrada anterior del curso: Teoremas sobre el límite de una función
• Siguiente entrada del curso: Límites en el infinito
• Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»