Introducción
Supongamos que tenemos un peso el cual hemos decidido invertir y, para hacerlo, tenemos tres opciones. La primera es invertir en el Banco A que está dispuesto a regresarnos un 100% de interés después de un año. En este caso, al finalizar el año tendríamos el doble de dinero que con el que iniciamos, es decir, tendríamos $ \$2.00.$
Nuestra segunda opción es el Banco B, que nos propone invertir nuestro dinero con ellos y promete generar el 50% del capital dos veces al año. Asumiendo que reinvertimos el dinero obtenido de tal forma que el capital inicial del segundo semestre es igual al capital final del primero, tendríamos lo siguiente
| Semestre | Interés | Capital inicial | Cálculo | Capital final |
|---|---|---|---|---|
| 1 | 50% / $\frac{1}{2}$ | $1.00 | $1 \cdot (1+\frac{1}{2})$ | $1.50 |
| 2 | 50% / $\frac{1}{2}$ | $1.50 | $1.5\cdot (1+\frac{1}{2})$ | $2.25 |
Notemos que el cálculo podemos hacerlo de forma directa mediante la siguiente expresión
$$\left(1 \cdot \left(1+\frac{1}{2} \right) \right) \cdot \left(1+\frac{1}{2} \right) = 1 \cdot \left(1+\frac{1}{2} \right)^2.$$
Por otro lado, la tercera opción, el Banco C, promete entregarnos 25% de interés cada trimestre. Si después de cada trimestre se invierte todo el capital inicial más los intereses generados, tenemos el siguiente escenario.
| Trimestre | Interés | Capital inicial | Cálculo | Capital final |
|---|---|---|---|---|
| 1 | 25% / $\frac{1}{4}$ | $1.00 | $1 \cdot (1+\frac{1}{4})$ | $1.25 |
| 2 | 25% / $\frac{1}{4}$ | $1.25 | $1.25 \cdot (1+\frac{1}{4})$ | $1.5625 |
| 3 | 25% / $\frac{1}{4}$ | $1.5625 | $1.5625 \cdot (1+\frac{1}{4})$ | $1.953125 |
| 4 | 25% / $\frac{1}{4}$ | $1.953125 | $1.953125 \cdot (1+\frac{1}{4})$ | $2.441406 |
De igual forma, podemos compactar los cálculos anteriores:
$$1 \cdot \left(1+\frac{1}{4} \right) \cdot \left(1+\frac{1}{4} \right) \cdot \left(1+\frac{1}{4} \right) \cdot \left(1+\frac{1}{4} \right) = 1 \cdot \left(1+\frac{1}{4} \right)^4.$$
Después de analizar todas las opciones, vemos que el Banco C nos permite generar más dinero al final del año siendo la mejor de nuestras tres opciones. Una interrogante natural después de haber evaluado los ejercicios anteriores es saber qué sucede si tenemos una tasa de interés de $\frac{1}{365}$ de forma diaria, lo cual generaría
$$1 \cdot \left(1 + \frac{1}{365} \right)^{365} = 2.714567.$$
Este escenario nos permite ganar una mayor cantidad de dinero al final del periodo. ¿Qué pasaría si tuviésemos una tasa de interés que se paga cada hora o cada minuto o cada segundo? Con una periodicidad lo suficientemente alta, ¿podríamos hacernos infinitamente ricos? Esta última pregunta la responderemos analizando el siguiente límite:
$$\lim_{n \to \infty} \left( 1 + \frac{1}{n} \right)^n.$$
El número de Euler
Después de la motivación dada en la introducción, definiremos la sucesión $\{e_n\}$ tal que $e_n = \left( 1 + \frac{1}{n} \right).$
Por los ejemplos revisados donde se calcula el interés en diferentes periodicidades, podemos inferir que la sucesión $\{e_n\}$ es creciente y a continuación lo probaremos.
Proposición. La sucesión $\{e_n\}$ es creciente.
Demostración.
Usando la fórmula del binomio de Newton se tiene lo siguiente
\begin{align*}
e_n & = \left( 1 + \frac{1}{n} \right)^n \\ \\
& = \sum_{ k = 0}^{n} { n \choose k } \frac{1}{n^k} \\ \\
& = \sum_{ k = 0}^{n} \frac{1}{k!} \cdot \frac{n (n-1) \ldots (n-k+1)}{n^k} \\ \\
& = \sum_{ k = 0}^{n} \frac{1}{k!} \cdot \frac{n}{n} \cdot \frac{n-1}{n} \ldots \frac{n-k+1}{n} \\ \\
& = \sum_{ k = 0}^{n} \frac{1}{k!} \cdot 1 \cdot \left( 1 – \frac{1}{n} \right) \ldots \left( 1 – \frac{k-1}{n} \right) \tag{1} \\ \\
& = 1 + 1 + \frac{1}{2!} \left(1 – \frac{1}{n} \right) + \frac{1}{3!} \left(1 – \frac{1}{n} \right) \left(1 – \frac{2}{n} \right) + \ldots + \frac{1}{n!} \left( 1 – \frac{1}{n} \right) \left( 1 – \frac{2}{n} \right) \ldots \left( 1 – \frac{n-1}{n} \right).
\end{align*}
$$\therefore e_n = 1 + 1 + \frac{1}{2!} \left(1 – \frac{1}{n} \right) + \frac{1}{3!} \left(1 – \frac{1}{n} \right) \left(1 – \frac{2}{n} \right) + \ldots + \frac{1}{n!} \left( 1 – \frac{1}{n} \right) \cdot \left( 1 – \frac{2}{n} \right) \ldots \left( 1 – \frac{n-1}{n} \right).$$
Análogamente, se tiene que
\begin{align*}
e_{n + 1} = & 1 + 1 + \frac{1}{2!} \left(1 – \frac{1}{n+1} \right) + \frac{1}{3!} \left(1 – \frac{1}{n+1} \right) \left(1 – \frac{2}{n+1} \right) + \ldots \\ \\
& + \frac{1}{n!} \left( 1 – \frac{1}{n+1} \right) \cdot \left( 1 – \frac{2}{n +1} \right) \ldots \left( 1 – \frac{n-1}{n+1} \right) \\ \\
& + \frac{1}{(n+1)!} \left( 1- \frac{1}{n+1} \right) \left( 1 – \frac{2}{n+1} \right) \ldots \left( 1 – \frac{n}{n+1} \right).
\end{align*}
Notemos que
$$\left( 1 – \frac{1}{n} \right) < \left( 1 – \frac{1}{n+1} \right), \ldots, \left( 1- \frac{k-1}{n} \right) < \left( 1- \frac{k-1}{n+1} \right).$$
Es decir, cada término de $e_n$ es más chico que su correspondiente de $e_{n+1}$ a partir del tercero. Además, $e_{n+1}$ tiene un término positivo extra, se sigue entonces que $e_n < e_{n+1}.$
Por tanto, $\{e_n\}$ es creciente.
$\square$
Antes de continuar, probaremos una proposición respecto a la serie geométrica.
Proposición. Sea $r \in \mathbb{R}$ tal que $|r|<1$, entonces
$$\sum_{k=0}^{n} r^k = \frac{1-r^{n+1}}{1-r}.$$
Demostración.
Sea $S_n = 1 + r + r^2 + r^3 + \ldots + r^n$. Entonces se tiene que
$$r \cdot S_n = r + r^2+r^3+r^4+\ldots+r^{n+1}.$$
Restando $S_n-rS_n$ se tiene
\begin{align*}
S_n-rS_n & = 1 + r + r^2 + r^3 + \ldots + r^n-(r + r^2+r^3+r^4+\ldots+r^{n+1}) \\
& = 1-r^{n+1}.
\end{align*}
\begin{gather*}
\Rightarrow & S_n-rS_n = 1-r^{n+1}. \\
\Rightarrow & S_n (1-r) = 1-r^{n+1}.
\end{gather*}
$$\therefore S_n = \frac{1-r^{n+1}}{1-r}.$$
$\square$
Al inicio se planteó la siguiente pregunta: con una periodicidad lo suficientemente alta, ¿podríamos hacernos infinitamente ricos? La respuesta es no y lo probamos en la siguiente proposición.
Proposición. La sucesión $\{e_n\}$ está acotada entre 2 y 3.
Demostración.
Dado que $\{ e_n\}$ es creciente, se tiene que $e_1 \leq e_n$ para todo $n \in \mathbb{N}$. Así, $e_1 = \left( 1 + \frac{1}{1} \right)^{1} = 2$. Por tanto, $2 \leq e_n$ para todo $n \in \mathbb{N}.$
Ahora probaremos que $3$ es una cota superior de la sucesión.
Notemos que $k! = 1 \cdot 2 \cdot 3 \ldots k \geq 1 \cdot 2 \cdot 2 \ldots 2 = 2^{k-1}$ y de $(1)$ tenemos que
\begin{align*}
e_n & = \sum_{k = 0}^{n} \frac{1}{k!} \cdot 1 \cdot \left( 1 – \frac{1}{n} \right) \ldots \left( 1 – \frac{k-1}{n} \right) \\ \\
& < \sum_{k = 0}^{n} \frac{1}{k!} \\ \\
& = 1 + \sum_{k = 1}^{n} \frac{1}{k!} \\ \\
& \leq 1 + \sum_{k = 1}^{n} \frac{1}{2^{k-1}} \\ \\
& = 1 + \sum_{k = 0}^{n-1} \frac{1}{2^{k}}.
\end{align*}
Además, por la proposición anterior se tiene que
$$ \sum_{k = 0}^{n-1} \frac{1}{2^k} = \frac{1 – \frac{1}{2^n}}{1- \frac{1}{2}} <2.$$
Por tanto, se sigue que $$1 + \sum_{k = 0}^{n-1} \frac{1}{2^{k}} < 3.$$
Se concluye que $2 < e_n < 3$.
$\square$
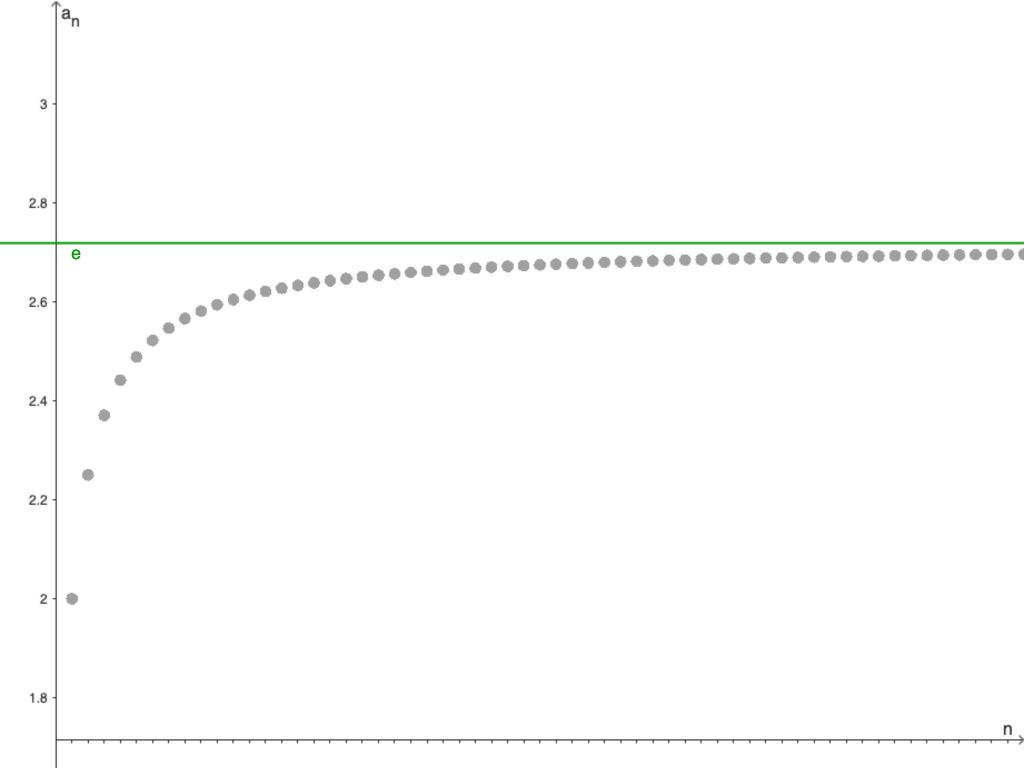
Hemos probado que $\{e_n\}$ es una sucesión creciente y acotada. Por tanto, se sigue que es convergente, y converge al supremo. Definimos el número de Euler de la siguiente forma:
$$e := \lim_{n \to \infty} \left( 1 + \frac{1}{n} \right)^n.$$
A continuación, mostramos la gráfica de esta sucesión.
Este número ha logrado posicionarse como uno de los más conocidos dentro del mundo de las matemáticas, siendo $e$ la base del logaritmo natural y dentro de este mismo curso se ha usado antes al momento de estudiar la función exponencial.
Más adelante…
En esta unidad hemos revisado a detalle el límite de una sucesión y en la unidad anterior estudiamos el concepto y propiedades de las funciones, es tiempo de continuar con un concepto más avanzado que requiere del entendimiento de ambos temas: el límite de una función.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
Encuentra los siguientes límites:
- $$\lim_{n \to \infty} \left(1+\frac{1}{n}\right)^{n+1}.$$
- $$\lim_{n \to \infty} \left(1+\frac{1}{n+1}\right)^n.$$
- $$\lim_{n \to \infty} \left(1+\frac{1}{n}\right)^{2n}.$$
- $$\lim_{n \to \infty} \left(1-\frac{1}{n}\right)^n.$$
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral I
- Entrada anterior del curso: Sucesiones de Cauchy
- Siguiente entrada del curso: Idea intuitiva de límite de una función
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»