Introducción

Anteriormente revisamos una definición intuitiva del límite con la finalidad de facilitar la comprensión de la definición formal. En esta entrada se dará la definición formal, así como algunos ejemplos para que el concepto sea comprendido en su totalidad.

Definición formal de límite

Retomemos la idea intuitiva a la que llegamos al final de la entrada anterior: logramos que $f$ se aproxime arbitrariamente, $\epsilon$, a $L$ siempre que logremos que $x$ esté lo suficientemente cerca, $\delta$, de $x_0$ sin ser $x_0.$

Observación. Notemos que la última parte la podemos expresar como $0<|x-x_0|<\delta$, pues al pedir que la distancia entre $x$ y $x_0$ sea mayor que $0$ se captura la idea de que $x\ne x_0$.

Es importante resaltar que estamos dando por hecho que se puede evaluar la función $f$ en valores de $x$ cercanos a $x_0$. Es por ello que se presenta la siguiente definición.

Definición. Sea $A\subset \mathbb{R}$. Un punto $x_0\in \mathbb{R}$ es un punto de acumulación de $A$ si para todo $\delta >0$ existe al menos un punto $x\in A$, $x\ne x_0$, tal que $|x-x_0|<\delta$.

Dada la definición anterior, si consideramos una función $f:A\to \mathbb{R}$, para calcular el límite, y asegurar que podemos evaluar $f$ en valores $x$ cercanos a $x_0$, deberemos pedir que $x_0$ sea punto de acumulación del dominio de la función, $A$. Con esto, tenemos todos los elementos para dar la definición de límite.

Definición. Sean $A\subset \mathbb{R}$ y $x_0$ un punto de acumulación de $A$. Para una función $f:A\to \mathbb{R}$, decimos que $L$ es el límite de $f$ en $x_0$ si para todo $\epsilon >0$ existe algún $\delta >0$ tal que, para todo $x\in A$, si $0<|x-x_0|<\delta$, entonces $|f(x)-L|<\epsilon .$

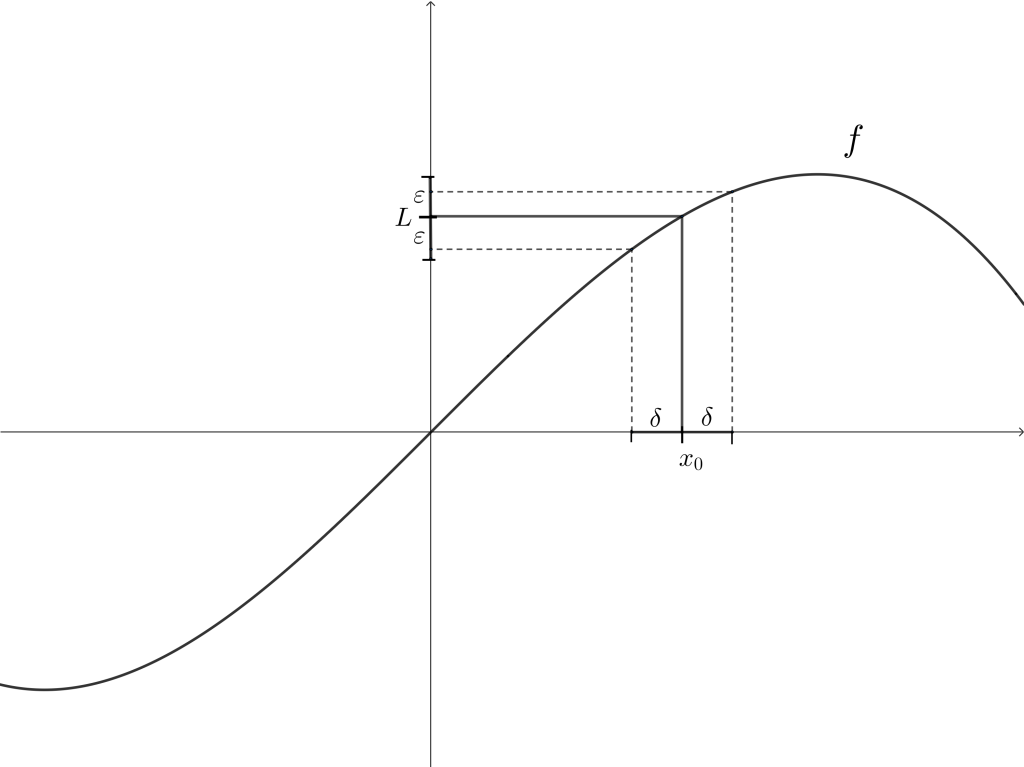
A continuación tenemos una imagen que nos permitirá visualizar la definición:

En la imagen podemos ver que si definimos un valor arbitrario $\epsilon >0$, entonces lo que buscamos es un valor positivo $\delta$, tal que si $x$ está a una distancia menor que $\delta$ con respecto a $x_0$, entonces eso implique que $f(x)$ esté a una distancia menor que $\epsilon$ con respecto a $L.$

A continuación revisaremos un ejemplo sencillo aplicando la definición.

Ejemplo 1. Demuestra que $$\underset{x\to -1}{lim}\frac{x^2-5x-6}{x+1}=-7.$$

Demostración.
Sea $\epsilon >0$. Notemos que si $x\ne -1$, entonces

$$\begin{array}{rl}|\frac{x^2-5x-6}{x+1}–(-7)|& =|\frac{x^2-5x-6}{x+1}+7|\\ \\ & =\left|\frac{x^2-5x-6+7x+7}{x+1}\right|\\ \\ & =\left|\frac{x^2+2x+1}{x+1}\right|\\ \\ & =\left|\frac{(x+1{)}^2}{x+1}\right|\\ \\ & =|x+1|.\end{array}$$
Tomemos entonces $\delta =\epsilon$. Si $0<|x-(-1)|=|x+1|<\delta$, entonces
$$|\frac{x^2-5x-6}{x+1}–(-7)|=|x+1|<\delta =\epsilon .$$
$$\therefore |\frac{x^2-5x-6}{x+1}–(-7)|<\epsilon .$$
$$\therefore \underset{x\to -1}{lim}\frac{x^2-5x-6}{x+1}=-7.$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Hagamos algunos comentarios respecto a la demostración. Como primer paso, establecimos un valor arbitrario positivo para $\epsilon$. Después hicimos algunas manipulaciones algebraicas que nos permitieron simplificar la expresión original en una más simple con la cual logramos encontrar el valor de $\delta$ que sería útil, en este caso, ese valor fue justamente el mismo que $\epsilon$.

Revisemos un segundo ejemplo.

Ejemplo 2. Sea $f(x)=\frac{3x+1}{2x}$, entonces $$\underset{x\to 2}{lim}f(x)=\frac{7}{4}.$$

Demostración.

Sea $\epsilon >0$. Veamos que

$$\begin{array}{rl}|f(x)–\frac{7}{4}|& =\left|\frac{3x+1}{2x}–\frac{7}{4}\right|\\ \\ & =\left|\frac{6x+2-7x}{4x}\right|\\ \\ & =\left|\frac{2-x}{4x}\right|\\ \\ & =\frac{|2-x|}{|4x|}\\ \\ & =\frac{|x-2|}{|4x|}\\ \\ & =\frac{1}{|4x|}\cdot |x-2|.\end{array}$$

De lo anterior, se sigue que
$$\begin{array}{}\text{(1)}& |f(x)–\frac{7}{4}|=\frac{1}{|4x|}\cdot |x-2|.\end{array}$$

Buscamos entonces acotar la expresión $(1)$, para ello podemos ver lo siguiente, si $|x-2|<1$, entonces

$$\begin{array}{cc}& |2|-|x|\le |x-2|<1.\end{array}$$

De lo anterior, se sigue que

$$\begin{array}{cc}& |2|-|x|<1.\\ \iff & 2-1<|x|.\\ \iff & 1<|x|.\\ \iff & 1>\frac{1}{|x|}.\\ \iff & \frac{1}{4}>\frac{1}{4|x|}=\frac{1}{|4x|}.\end{array}$$

Por tanto, se tiene que

$$\begin{array}{}\text{(2)}& \frac{1}{|4x|}<\frac{1}{4}.\end{array}$$

Entonces si $|x-2|<1$, por (1) y (2), tenemos lo siguiente
$$\begin{array}{rl}|f(x)–\frac{7}{4}|& =\frac{1}{|4x|}\cdot |x-2|\\ \\ & <\frac{1}{4}\cdot |x-2|.\end{array}$$

Previamente acotamos $|x-2|$ por el valor $1$, pero de la última expresión se sigue que deberemos acotarlo también por $4\epsilon$ para llegar a nuestro objetivo, tomemos así $\delta =min\{1,4\epsilon \}.$

Si $0<|x-2|\le \delta$. Es decir, si $|x-2|\le 1$ y $|x-2|\le 4\epsilon$, entonces
$$|f(x)–\frac{7}{4}|<\frac{1}{4}|x-2|\le \frac{1}{4}\cdot 4\epsilon .$$
$$\therefore |f(x)–\frac{7}{4}|<\epsilon .$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Nuevamente haremos énfasis en los pasos generales de la demostración. Iniciamos dando un valor de $\epsilon$ arbitrario, y la tarea es encontrar el valor $\delta >0$ que acote la distancia entre $x$ y $x_0=2$ de tal manera que los valores de la función $f$ se aproximen a $L$ lo suficiente para que su distancia sea menor que $\epsilon .$

Trabajemos ahora sobre el siguiente ejemplo.

Ejemplo 3. Para todo $x_0\in \mathbb{R}$ se tiene que $$\underset{x\to x_0}{lim}{x}^2=x_0^2.$$

Demostración.

Sea $\epsilon >0$ y $x_0\in \mathbb{R}$. Notemos que

$|x^2–x_0^2|=|x-x_0||x+x_0|.$

Haciendo uso de una manipulación análoga al del ejemplo anterior, podemos ver que si $|x-x_0|<1$, entonces

$|x|-|x_0|\le |x-x_0|<1\Rightarrow |x|<1+|x_0|.$

Cabe resaltar que en el ejemplo anterior usamos la propiedad $|x_0|-|x|\le |x-x_0|$, ya que la intención es acotar al recíproco de $x$. En este caso, se emplea $|x|-|x_0|\le |x-x_0|$, puesto que buscamos acotar directamente a $x$.

Además,
$$\begin{array}{rl}|x+x_0|& \le |x|+|x_0|\\ & <1+|x_0|+|x_0|\text{, pues}|x|<1+|x_0|\\ & =1+2|x_0|.\end{array}$$

Así, tenemos que $$|x+x_0|<1+2|x_0|.$$

En esta ocasión queremos que $|x-x_0|<1$ y, por la última expresión, también queremos que $|x-x_0|<\frac{\epsilon }{1+2|x_0|}$, definimos así $\delta =min\{1,\frac{\epsilon }{1+2|x_0|}\}$. Si $0<|x-x_0|<\delta$, entonces

$$\begin{array}{rl}|x^2-x_0^2|& =|x-x_0||x+x_0|\\ \\ & <|x-x_0|(1+2|x_0|)\\ \\ & <\delta (1+2|x_0|)\\ \\ & \le \frac{\epsilon }{1+2|x_0|}\cdot (1+2|x_0|)\\ \\ & =\epsilon .\end{array}$$

Esto implica que
$$|x^2-x_0^2|<\epsilon .$$
$$\therefore \underset{x\to x_0}{lim}{x}^2=x_0^2.$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Unicidad del límite de una función

Después de haber revisado estos ejemplos, la definición de límite de una función (también llamada definición épsilon-delta), estamos listos para revisar la primera propiedad del límite.

Proposición. El límite de una función en $x_0$ es único, es decir, si $f$ tiende a $L$ en $x_0$ y $f$ tiende a $L^{\prime }$ en $x_0$, entonces $L=L^{\prime }.$

Demostración.
Sea $\epsilon >0$. Como $f$ tiende a $L$ y $L^{\prime }$ en $x_0$, entonces para $\frac{\epsilon }{2}>0$ existen ${\delta }_1>0$ y ${\delta }_2>0$ tales que

$$\begin{array}{c}\text{Si }0<|x-x_0|<{\delta }_1\Rightarrow |f(x)-L|<\frac{\epsilon }{2}.\\ \text{Si }0<|x-x_0|<{\delta }_2\Rightarrow |f(x)-L^{\prime }|<\frac{\epsilon }{2}.\end{array}$$

Consideremos ahora $\delta =min\{{\delta }_1,{\delta }_2\}$. Entonces si $0<|x-x_0|<\delta$ y, por la desigualdad del triángulo, esto implica que

$$\begin{array}{rl}|L-L^{\prime }|\le & |L-f(x)|+|L^{\prime }-f(x)|\\ <& \frac{\epsilon }{2}+\frac{\epsilon }{2}\\ =& \epsilon .\end{array}$$

Se sigue que

$|L-L^{\prime }|<\epsilon .$

Como $\epsilon$ es un valor arbitrario positivo, podemos concluir que $L-L^{\prime }=0$, es decir, $L=L^{\prime }.$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Más adelante…

En la siguiente entrada revisaremos con detalle varias propiedades que tienen los límites para lo cual haremos uso de una bella relación existente entre el límite de una sucesión y el de una función. Una vez revisadas estas propiedades, el cálculo de los límites se hará considerablemente más simple.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Usando la definición épsilon-delta, demuestra lo siguiente:

• $$\underset{x\to x_0}{lim}c=c.$$
• $$\underset{x\to x_0}{lim}x=x_0.$$
• $$\underset{x\to 5}{lim}x+11=16.$$
• $$\underset{x\to -2c}{lim}(2c-3x)=8c.$$
• $$\underset{x\to 0}{lim}\frac{x^2}{|x|}=0.$$

Entradas relacionadas

• Ir a Cálculo Diferencial e Integral I
• Entrada anterior del curso: Idea intuitiva de límite de una función
• Siguiente entrada del curso: Límite de una función a través de sucesiones
• Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»