Introducción

En esta última entrada de la unidad veremos un poco sobre la cardinalidad de un conjunto, un par de definiciones para decir cuando un conjunto es infinito o finito y algunos teoremas útiles. Dado que se trata de un tema adicional varios de los teoremas y resultados sólo serán enunciados.

Cardinalidad de un conjunto

Definición (Cardinalidad): Sea $A$ un conjunto. Definimos a la cardinalidad de $|A|$ como una medida que indica el número de elementos en dicho conjunto $A$ y la denotaremos como:
$$|A|.$$

Ejemplo: Sea $A= \left\{ 1,2,3,g,y,b \right\}$ así tenemos que su cardinalidad sería:
$$|A|=6.$$

Definición: Decimos que $|A| \leq |B|$ si existe una función $f: A \rightarrow B$ inyectiva.

Misma cardinalidad

Definición: Sean $A,B$ conjuntos. Decimos que $A$ y $B$ tienen la misma cardinalidad $$|A|=|B|,$$ si existe una función $f: A \leftrightarrow B$ biyectiva.

Para los fines de esta entrada, daremos la definición de función biyectiva. Revisaremos esta definición con mayor detenimiento en la unidad 3, dedicada a las funciones, como parte de este curso.

Definición: Sea $f: A \rightarrow B$ una función. Decimos que $f$ es biyectiva si cumple con ser inyectiva y sobreyectiva.

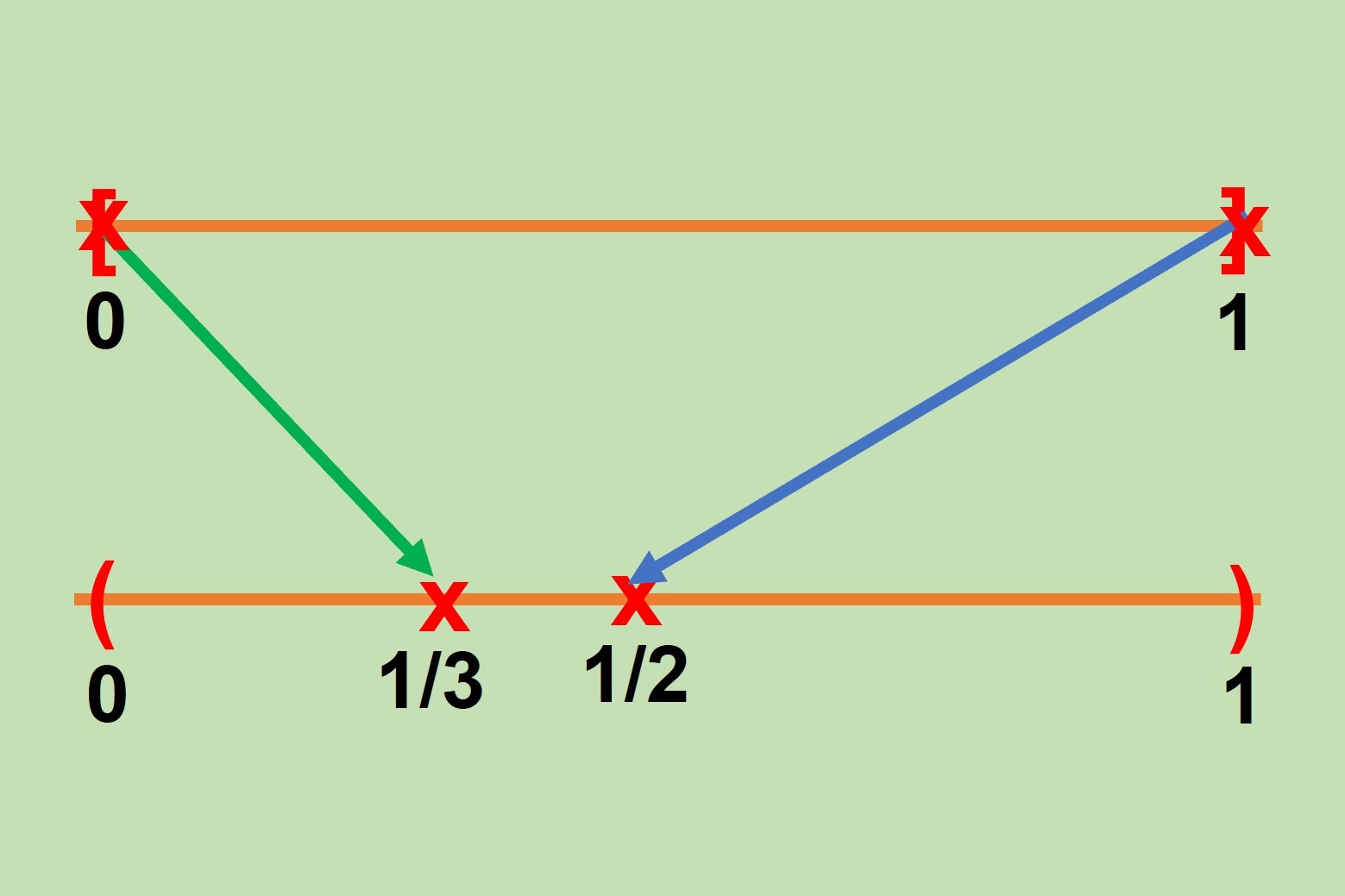
Ejemplo: Si consideramos los intervalos $[0,1]$ y $(0,1)$. Vemos que:
$$|[0,1]| = |(0,1)|.$$
Primero tomamos los valores $0$ y $1$ en el intervalo $[0,1]$ y los enviamos a los valores $\frac{1}{3}$ y $\frac{1}{2}$ respectivamente en el intervalo $(0,1)$.

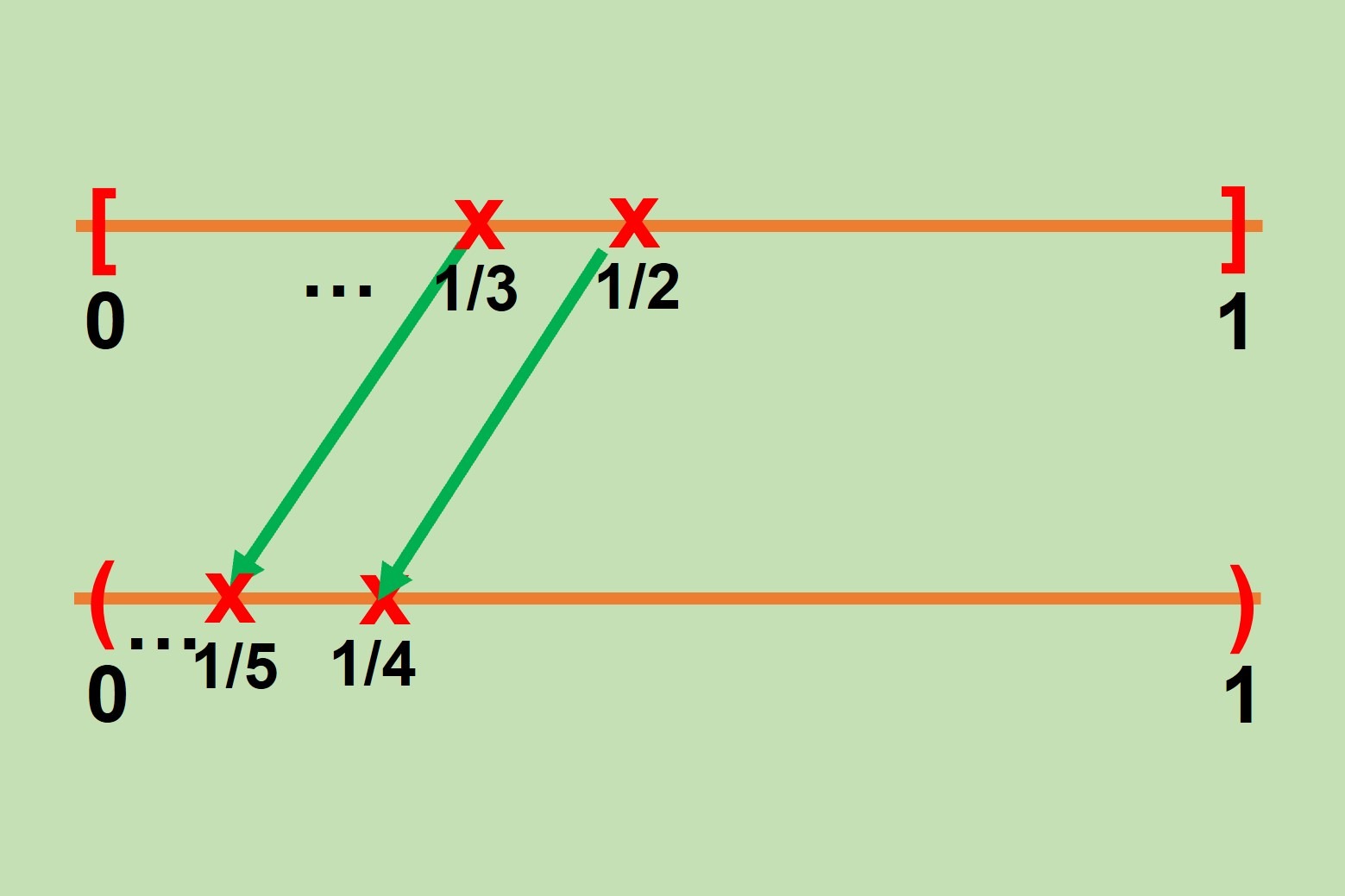
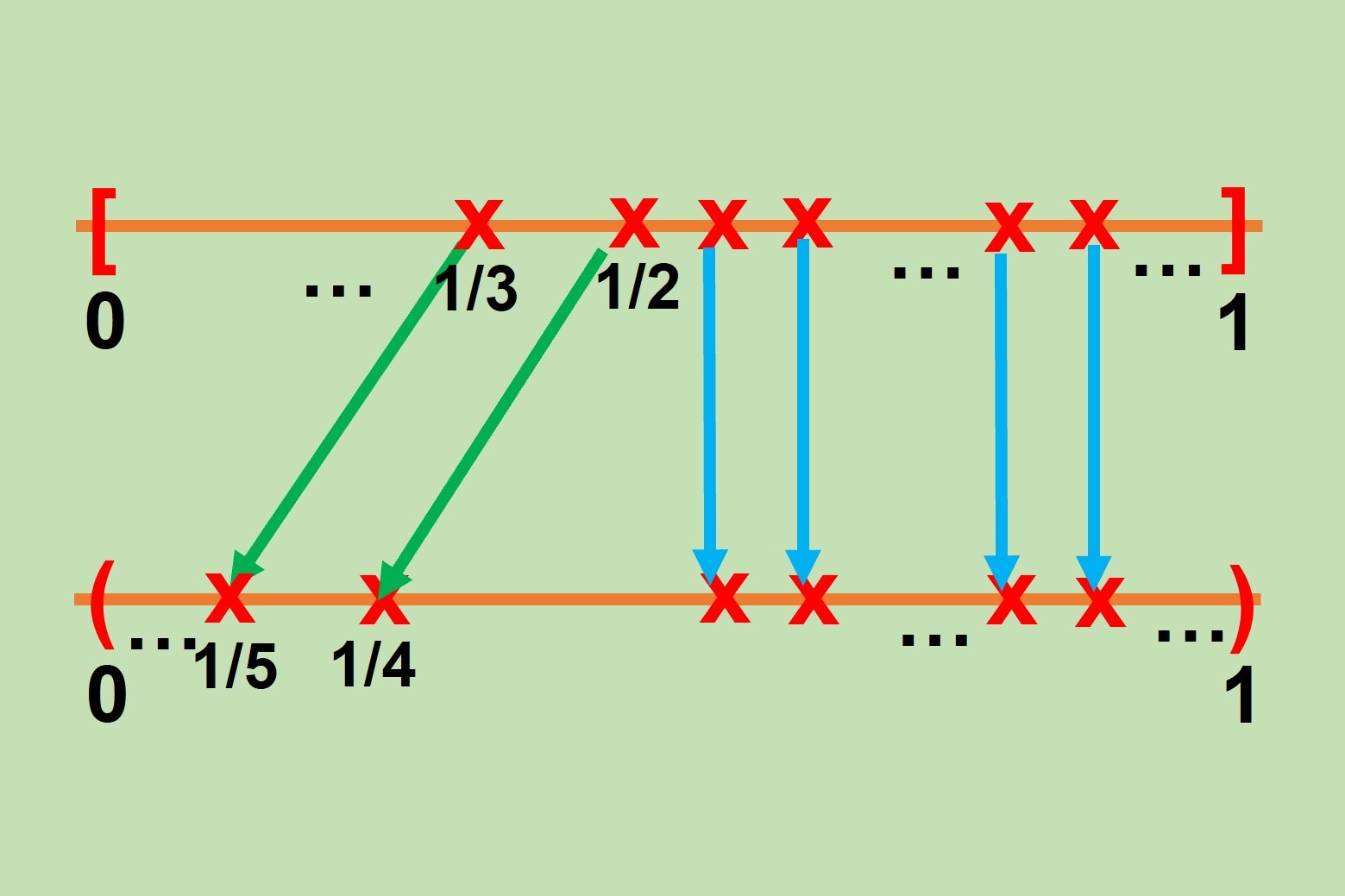
Ahora consideramos los valores de la forma $\frac{1}{n}$ con $n \in \mathbb{N}\setminus \left\{0\right\}$ y $n \geq 2$. A estos valores los enviaremos a los de la forma $\frac{1}{n+2}$. De este modo lo que haremos será enviarlos al $(0,1)$ como en el ejemplo de la siguiente imagen:

Y por último, a los valores restantes los enviamos a ellos mismos en el intervalo $(0,1)$.

Así la función biyectiva sería $f: [0,1] \leftrightarrow (0,1)$:
\begin{equation*}
f(x)=
\begin{cases}
x &\text{si $x \neq 0,1,\frac{1}{n}$ con $n\geq 2$}\\
\frac{1}{2} & \text{si $x= 1$}\\
\frac{1}{3} &\text{si $x=0$}\\
\frac{1}{x+2} &\text{si $x = \frac{1}{n}$ con $n\geq 2$}\\
\end{cases}
\end{equation*}

Conjuntos finitos e infinitos

Definición (1): Sea $A$ un conjunto.

• $A$ es finito si existe una función biyectiva $f: A \leftrightarrow \left\{1,2, \cdots , N \right\}$ para algún $N \in \mathbb{N}\setminus \left\{0\right\}$.
• $A$ es infinito si no es finito.

Definición (2): Sea $A$ un conjunto.

• $A$ es infinito si existe $A’ \subset A$ subconjunto propio de A y una función biyectiva $f: A’ \leftrightarrow A$.
• $A$ es finito si no es infinito.

Teorema: Sean $A,B$ conjuntos no vacíos. Si $A \subseteq B$ entonces
$$|A| \leq |B|.$$
Demostración: Proponemos a la función $f: A \rightarrow B$ como $f(x)=x$. Observamos que $f$ es inyectiva y cumple que para todo $x \in A$ se sigue que $x \in B$. Por definición se sigue que $|A| \leq |B|.$

$\square$

Observación: Si $A,B$ son conjuntos infinitos puede ocurrir que $A \subset B$ y que $|A|=|B|.$

Teorema: Sean $A,B$ conjuntos finitos.

• Si $A \cap B = \emptyset$ entonces:
  $|A \cup B|= |A|+|B|.$
• Si $A \cap B \neq \emptyset$ entonces:
  $|A \cup B|= |A|+|B|-|A \cap B|.$

Definición (3): Un conjunto $A$ es infinito si existe $B \subseteq A$ tal que
$$|B|=|\mathbb{N}|.$$

Conjuntos numerables

Definición: Sea $A$ un conjunto no vacío. Decimos que $A$ es numerable si $|A|=|\mathbb{N}|$ es decir si existe una función biyectiva:
$$f: A \rightarrow \mathbb{N}.$$

Teorema: Sean $A,B$ conjuntos. Si $A$ es finito y $B$ es infinito numerable entonces $A \cup B$ es numerable.
Demostración: Como $A$ es finito consideremos que tiene $m$ elementos.
$$A = \left\{ a_{1}, a_{2}, \cdots , a_{m} \right\}.$$
Y como $B$ es infinito y numerable entonces es de la forma:
$$B = \left\{ b_{1}, b_{2}, \cdots , b_{n}, \cdots \right\}.$$
Así al considerar la unión $A \cup B$ tendríamos:
$$A \cup B = \left\{ a_{1}, a_{2}, \cdots , a_{m}, b_{1}, b_{2}, \cdots , b_{n}, \cdots \right\}.$$
Tenemos los siguientes dos casos:

• Si $A\cap B = \emptyset$ y consideramos la siguiente indización:
  $$A \cup B = \left\{ a_{1}, a_{2}, \cdots , a_{m}, b_{m+1}, b_{m+2}, \cdots , b_{m+n}, b_{m+n+1}, \cdots \right\}.$$
  Vemos $|A \cup B|=|\mathbb{N}|.$
• Si $A\cap B \neq \emptyset$. Supongamos que tenemos $k$ elementos en la intersección, es decir:
  $$a_{1}= b_{1}, a_{2}= b_{2}, \cdots , a_{k}= b_{k}$$
  $$A = \left\{ a_{1}, a_{2}, \cdots ,a_{k}, a_{k+1}, \cdots, a_{m} \right\}.$$
  Así consideramos la siguiente indización para la unión:
  $$A \cup B = \left\{ a_{k+1}, a_{k+2}, \cdots , a_{m}, b_{1}, b_{2}, \cdots , b_{n}, \cdots \right\}.$$
  Observamos que $|A \cup B|=|\mathbb{N}|.$
  

$\square$

Teorema: Si $A$ y $B$ son conjuntos infinitos y numerables entonces $A \cup B$ es infinito y numerable.
Demostración: Primero vemos que $A \cup B$ es infinito ya que al ocurrir que:

• $A \subseteq A \cup B$ con $A$ infinito y numerable.
• $B \subseteq A \cup B$ con $B$ infinito y numerable.

por definición (3) concluimos que $A \cup B$ es infinito.

Nos falta ver qué $A \cup B$ es numerable, ya que $A$ es numerable podemos escribirlo de la siguiente manera:
$$A = \left\{ a_{1}, a_{2}, \cdots \right\}.$$
Análogamente para $B$:
$$B = \left\{ b_{1}, b_{2}, \cdots \right\},$$
por lo que la unión se vería como:
$$A \cup B= \left\{ a_{1}, b_{1},a_{2}, b_{2},a_{3},b_{3} \cdots, a_{n}, b_{n}, \cdots \right\}.$$
Observemos que si consideramos la siguiente indización:
$$A \cup B= \left\{ a_{1}, b_{2},a_{3}, b_{4},a_{5},b_{6} \cdots, a_{2n-1}, b_{2n}, \cdots \right\},$$

el conjunto tiene una relación biunívoca con el conjunto de los naturales.
Veamos qué sucede en los siguientes casos:

• Si $A \cap B = \emptyset \Rightarrow |A \cup B|=|\mathbb{N}|.$
• Si $A \cap B \neq \emptyset$. Consideremos que existen k elementos en la intersección, por lo que serían de la forma:
  $$a_{1}= b_{1}, a_{2}= b_{2}, \cdots , a_{k}= b_{k}.$$
  Por lo que ahora la unión se vería como:
  $$A \cup B= \left\{ a_{1}, a_{2}, a_{3}, \cdots,a_{k}, a_{k+1}, b_{k+1},a_{k+2}, b_{k+2} \cdots, a_{k+n}, b_{k+n}, \cdots \right\}$$
  y si consideramos la siguiente nueva indización:
  $$A \cup B= \left\{ a_{1}, a_{2}, a_{3}, \cdots,a_{k}, a_{k+1}, b_{k+2},a_{k+3}, b_{k+4} \cdots, a_{k+(2n-1)}, b_{k+2n}, \cdots \right\},$$
  tenemos que tiene una relación biunívoca con $\mathbb{N}$ por lo que también se cumple que $|A \cup B|=|\mathbb{N}|$.

$\square$

A continuación enunciaremos un teorema que generaliza el resultado sobre conjuntos numerables ya visto.

Teorema: Sean $A_{1}, A_{2}, \cdots, A_{N}, \cdots $ conjuntos no vacíos.

• Si $A_{1}, A_{2}, \cdots, A_{N}$ son numerables $\Rightarrow \begin{multline*} \bigcup_{i=1}^{N} A_{i} \end{multline*}$ es numerable.
• Si $A_{1}, A_{2}, \cdots$ son numerables $\Rightarrow \begin{multline*} \bigcup_{i=1}^{\infty} A_{i} \end{multline*}$ es numerable.

Más adelante

Ahora que hemos concluido con la unidad relacionada a los Números reales, en la próxima iniciaremos el tema de funciones definiendo qué es el dominio, rango y regla de correspondencia de una función.

Entradas relacionadas

• Ir a: Cálculo Diferencial e Integral I
• Entrada anterior del curso: Cálculo Diferencial e Integral I: Cortaduras de Dedekind (Adicional).
• Entrada siguiente del curso: Cálculo Diferencial e Integral I: Concepto de función.
• Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»