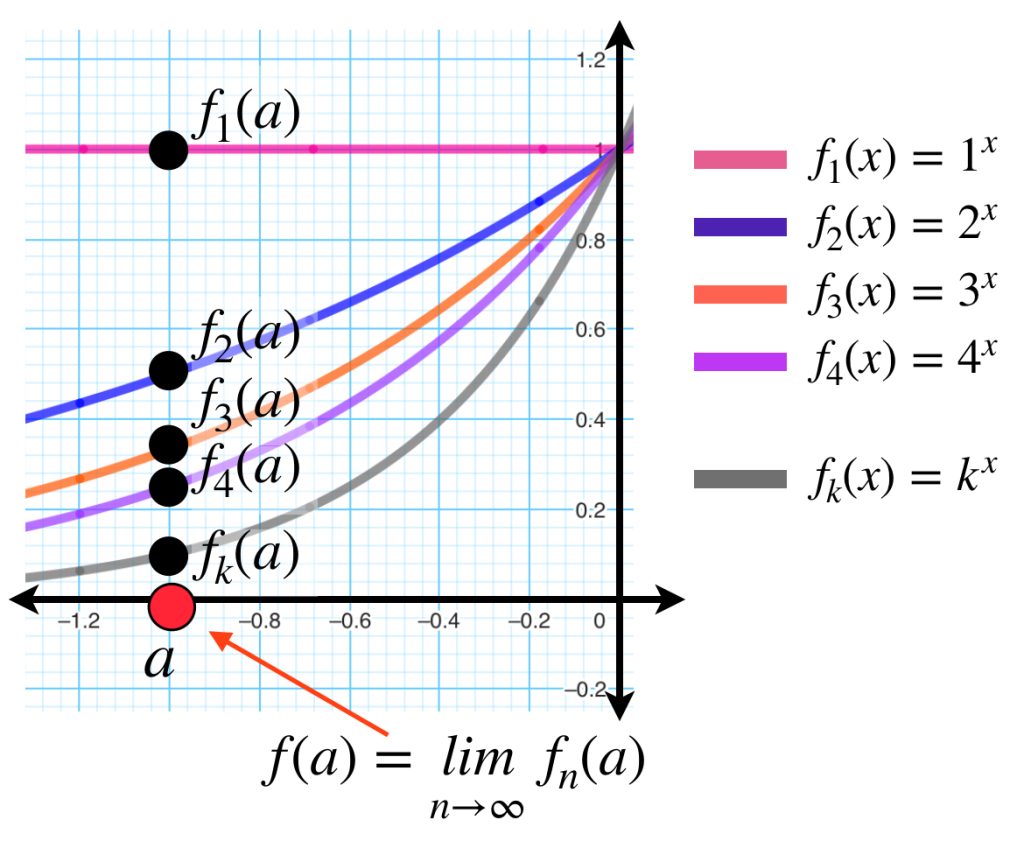
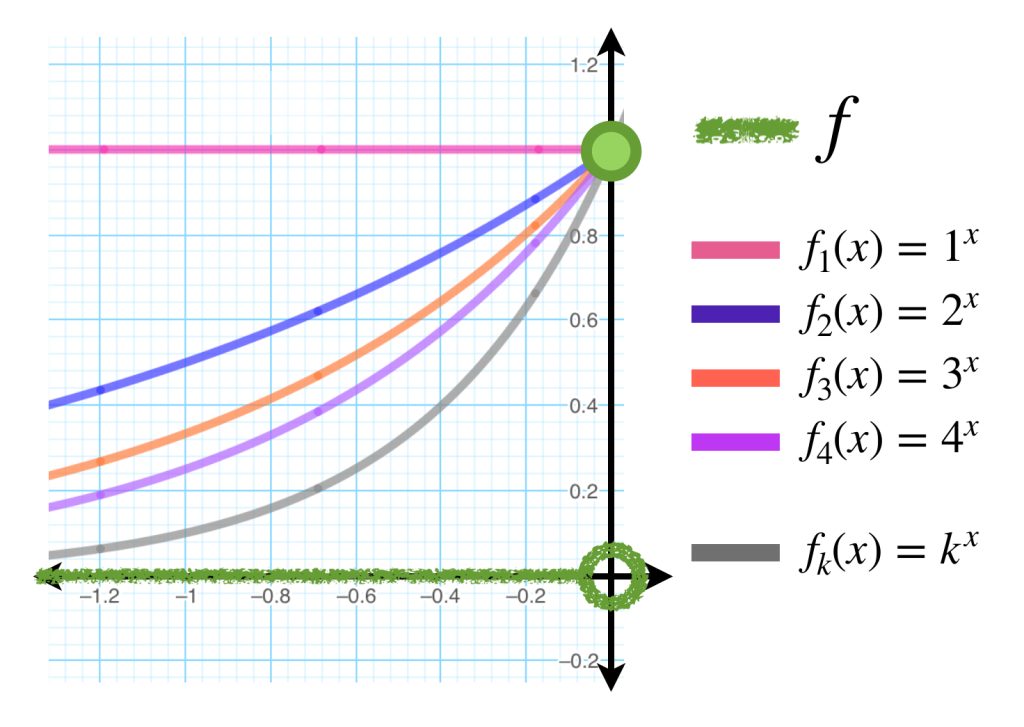
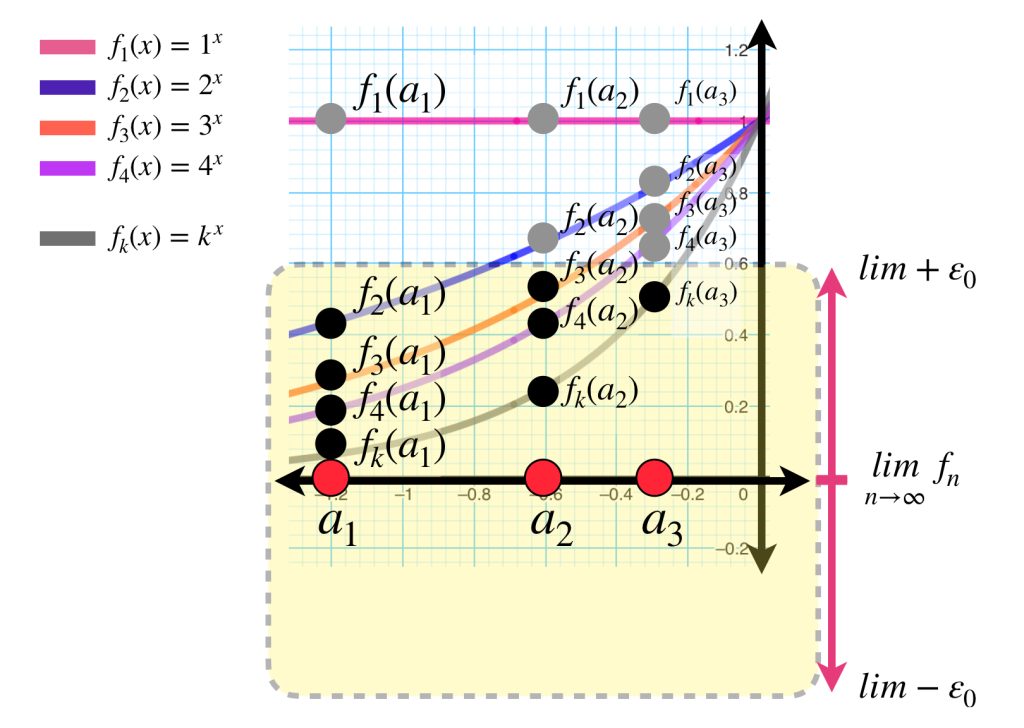
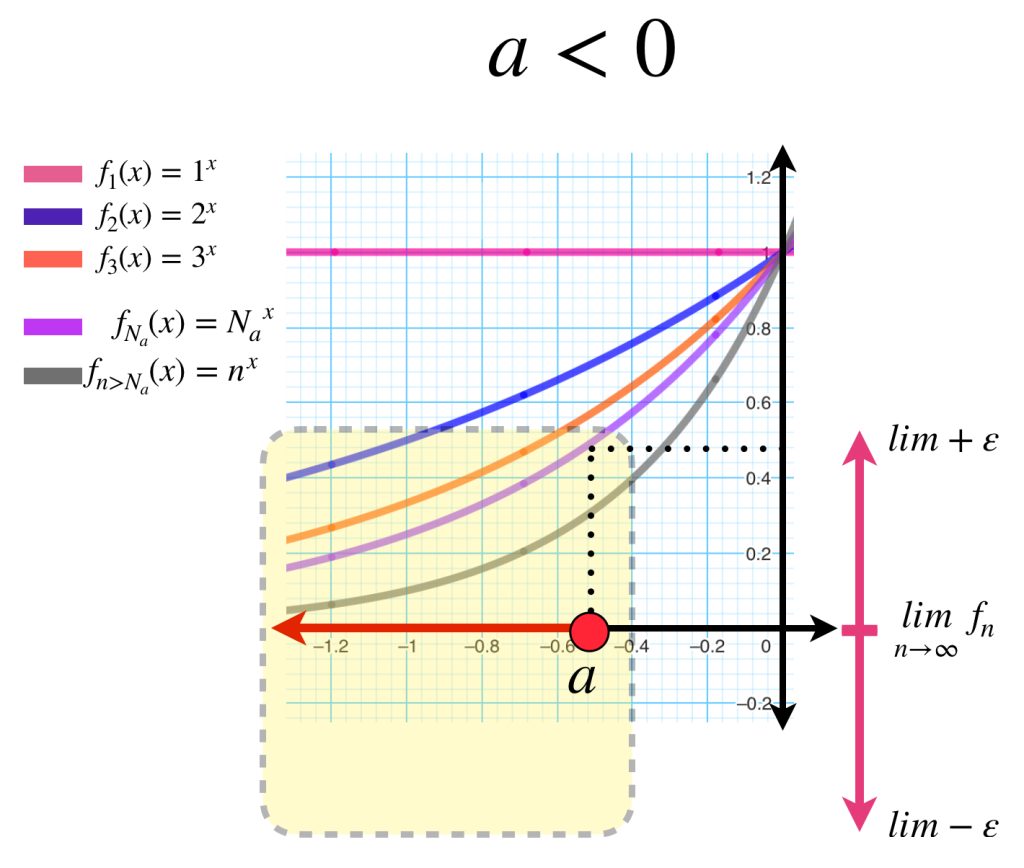
Introducción

En la entrada Contracciones mencionamos el teorema de punto fijo de Banach. Ahí mismo demostramos que si una contracción tiene un punto fijo, entonces este es único. En la entrada anterior vimos que la sucesión generada a partir de una contracción $\phi \,$ y un punto cualquiera $x_0$ del espacio métrico es de Cauchy. Estos dos resultados serán usados a continuación para exponer una demostración del teorema. Recordemos lo que expresa:

Teorema de punto fijo de Banach. Sea $(X,d)$ un espacio métrico completo y sea $\phi:X \to X$ una contracción, entonces:

1. Para cada $x_0 \in X$ la sucesión $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ es de Cauchy y, en consecuencia $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ converge a un punto $x^* \in X.$ $\, \, \phi^n$ representa la composición $\, \underset{n \, veces}{\underbrace{ \phi \circ … \circ \phi }}$
2. El punto $x^*$ descrito es punto fijo de $\phi.$
3. El punto fijo es único.
4. Podemos estimar la distancia de $\phi ^n(x_0)$ a $x^*$ usando la desigualdad:
   $$d( \phi ^n(x_0),x^*) \leq \frac{\alpha^n}{1-\alpha} \, d( x_0,\phi (x_0))$$

Demostración:
1. Se probó en la entrada anterior que la sucesión $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ es de Cauchy. Como aquí agregamos el hecho de que el espacio es completo, concluimos que converge a algún punto $x^* \in X.$

2. Sea $x^* = \underset{n \to \infty}{lim}\, \phi ^n(x_0).$ Probemos que $x^*$ es punto fijo de $\phi.$
Sea $x_n= \phi^n(x_0).$ Apliquemos a cada término la función $\phi$ que como es contracción, entonces es Lipschitz y por tanto es continua, tal como se vio en la entrada Más conceptos de continuidad.

Como
$$(x_n)_{n \in \mathbb {N}} \to x^*$$
se sigue por lo visto en la entrada Funciones continuas en espacios métricos que
$$(\phi(x_n))_{n \in \mathbb {N}} \to \phi(x^*)$$
Pero para cada $n \in \mathbb{N}, \, \phi(x_n)= (x_{n+1})$ de modo que $(\phi(x_n))_{n \in \mathbb {N}}$ es una subsucesión de $(x_n)_{n \to \mathbb {N}} \to x^*.$ En consecuencia $(\phi(x_n))_{n \in \mathbb {N}}$ también converge a $x ^*.$
Pero por la unicidad del límite se sigue que.
$$ \phi(x^*) = x^*$$
Lo cual demuestra que $x^*$ es punto fijo de $\phi.$

3. Se probó en Contracciones.

4. En la demostración vista en la entrada anterior vimos que existe $N \in \mathbb{N}$ tal que si $n,m \geq N$ entonces

$$d(x_n,x_m) \leq \dfrac{\alpha^n}{1-\alpha} \, d( x_0,x_1)$$

Haciendo tender $m \to \infty$ se sigue que

$$d(x_n,x^*) \leq \dfrac{\alpha^n}{1-\alpha} \, d( x_0,x_1)$$

Por lo tanto

$$d(\phi^n(x_0),x^*) \leq \dfrac{\alpha^n}{1-\alpha} \, d( x_0,\phi(x_0)).$$

Que es lo que queríamos demostrar. Nota que esta última desigualdad nos permite acercarnos arbitrariamente al punto fijo de la contracción $\phi$ incluso sin conocerlo, pues su lado derecho puede elegirse tan pequeño como se desee, eligiendo un valor para $n$ suficientemente grande.

Ejemplo: $\phi : \mathbb{C} \to \mathbb{C}, \, \phi(z) = \dfrac{3iz}{4}$

Considera el espacio métrico completo $\mathbb{C}$ con la norma usual. Dejaremos como ejercicio probar que $\phi : \mathbb{C} \to \mathbb{C}, \, \phi(z) := \dfrac{3iz}{4}$ es contracción. La siguiente imagen muestra las primeras iteraciones de $\phi$ partiendo de $x_0 = 1.$ ¿A qué punto converge?

Si $n = 20,$ ¿puedes decir qué tan cerca está $\phi ^n(1)$ del punto fijo? Nota que puedes hacer una estimación sin tener que calcular la norma del punto $\phi ^n(1).$ Da el valor de $N \in \mathbb{N}$ a partir del cual la distancia al punto fijo sea menor que $\dfrac{1}{100}.$

Más adelante…

Veremos el teorema de punto fijo de Banach aplicado en la demostración de la existencia y unicidad de la solución de una ecuación diferencial. Esto es, se buscan las funciones que satisfacen cierta ecuación. Estas funciones serán vistas como elementos de un espacio métrico completo. Como llegaremos a que la solución existe y es única, podemos esperar que dicha solución será punto fijo del espacio bajo cierta contracción.

Tarea moral

1. Resuelve las preguntas planteadas en el ejemplo arriba mencionado.
2. Considera el espacio de sucesiones acotadas en $\mathbb{R}$ con norma $\norm{(x_n)_{n \in \mathbb{N}}}_\infty := \underset{n \in \mathbb{N}}{sup}\, |x_n|.$
   a) Demuestra que la función $\phi(x_n)_{n \in \mathbb{N}}= (\frac{1}{2}(x_n))_{n \in \mathbb{N}} \,$ es contracción.
   b) Si $(x_0)$ es la sucesión acotada $(x_{0_n})_{n \in \mathbb{N}}.$ ¿Qué valores de $n \in \mathbb{N}$ satisfacen que la distancia entre $\phi^n(x_0)$ y la sucesión que es el punto fijo de $\phi$ sea menor que $\dfrac{1}{100}?$
3. Sea $X$ un espacio metrico y $\phi:X \to X$ una contracción. Demuestra que:
   a) Para cada $n \in \mathbb{N},$ la función $\phi^n$ es contracción.
   b) Si $x^*$ es punto fijo de $\phi,$ también lo es de $\phi^n.$
   c) Si $\psi: X \to X$ satisface que $\psi \circ \phi = \phi \circ \psi$ entonces $\psi$ tiene un punto fijo.
   d) Si $x^*$ es punto fijo para $\phi^k$ y para $\phi^{k+1}$ para algún $k \geq 2$ entonces $x^*$ es el punto fijo de $\phi.$

Bibliografía

• Apostol, T., Análisis Matemático (2a ed.). México: Editorial Reverté, 1996. Págs: 111 y 112.
• Clapp, M., Análisis Matemático. Ciudad de México: Editorial Papirhos, IM-UNAM, 2013. Págs: 99-101 y 116.
• Jost, J., Postmodern Analysis (3rd ed.). New York: Springer-Verlag, 2005. Págs: 43 y 44.
• Kolmogorov, A.N., Fomin, S.V., Elementos de la Teoría de Funciones y del Análisis Funcional. (2a ed.). Moscú: Editorial MIR, 1975. Págs: 79 y 80.
• Rudin, W., Principles of Mathematical Analysis (3rd ed.). New York: McGraw–Hill, 1953. Págs: 220 y 221.

Enlaces

• Análisis Matemático.
• Guía de notación para Análisis Matemático I
• Enlace a entrada anterior.
• Enlace a entrada siguiente.

Introducción

En esta entrada continuaremos con la demostración del teorema de punto fijo de Banach, enunciado en la sección anterior. Vimos dos ejemplos de contracciones donde generamos una sucesión a partir de cualquier punto del espacio, evaluando la contracción recursivamente. En nuestros ejemplos observamos que la sucesión creada es convergente. ¿Lo será con cualquier contracción? Por lo pronto mostraremos que una sucesión así definida es de Cauchy.

Comencemos comprobándolo para el siguiente caso. Es más general que la primera función vista en Contracciones.

Ejemplo: $f(x)= \alpha x.$

En el espacio euclidiano $\mathbb{R}$ considera $f:\mathbb{R} \to \mathbb{R}$ definida como $f(x)= \alpha x,$ con $\alpha \in (0,1)$ constante. Entonces:
$$d(f(x),f(y))=d(\alpha \, x, \alpha \, y)=|\alpha \, x- \alpha \, y|= \alpha|x-y|=\alpha \, d(x,y)$$
Lo cual prueba que $f$ es contracción.

Veamos ahora que la sucesión generada al evaluar $f,$ partiendo de $x_0 \in \mathbb{R}$ es de Cauchy. Dado $x_0 \in \mathbb{R}$ tenemos:

$x_1:=f(x_0) = \alpha x_0$
$x_2:=f(x_1) = \alpha x_1 = \alpha^2 x_0$
$x_3:=f(x_2) = \alpha x_2 = \alpha^3 x_0$
.
.
.
$x_k:=f(x_{k-1}) = \alpha x_{k-1}= \alpha^k x_0$

Entonces la sucesión está dada por $(\alpha^n x_0)_{n \in \mathbb{N}}.$ Probemos que es de Cauchy en $\mathbb{R}.$

A continuación, $ln(x)$ hace referencia al logaritmo natural de $x.$

Sea $\large{\varepsilon} >0$ y sea $N \in \mathbb{N}$ tal que $N > \dfrac{ln \left(\frac{\large{\varepsilon}}{|x_0|} \right)}{ln(\alpha)}.$

Como $\alpha \in (0,1), \, ln(\alpha)< 0.$ Se sigue que:

\begin{align*}
& &N \, ln(\alpha) &< ln \left(\frac{\varepsilon}{|x_0|} \right) \\
&\Rightarrow \, &exp \left(ln \left(\alpha^N \right) \right) &< exp \left( ln \left( \frac{\varepsilon}{|x_0|} \right) \right) \\
&\Rightarrow \, &\alpha^N&< \frac{\varepsilon}{|x_0|}
\end{align*}

La última desigualdad se usará en las siguientes líneas.

Sean $n,m \geq N.$ Supón sin pérdida de generalidad que $n \leq m$ entonces $\alpha^n \geq \alpha^m \geq 0 .$ Tenemos:

\begin{align*}
d(x_n,x_m) &= |x_n-x_m|\\
&=|\alpha^n x_0 \, – \, \alpha ^m x_0|\\
&= |\alpha ^n – \alpha^m||x_0|\\
&\leq \alpha ^n|x_0| \\
&\leq \alpha ^N |x_0| \\
&< \frac{\varepsilon}{|x_0|}|x_0| \\
&= \varepsilon
\end{align*}

Por lo tanto la sucesión $(\alpha^n x_0)_{n \in \mathbb{N}} \,$ es de Cauchy.

Pasemos a demostrar el caso general:

Proposición. Sea $(X,d)$ un espacio métrico, $\phi : X \to X$ una contracción con constante $\alpha \in (0,1)$ y sea $x_0 \in X.$ Entonces la sucesión $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ es de Cauchy en $X.$

Demostración:
Comencemos con un análisis entre distancias de los primeros pares de puntos de la sucesión.

\begin{align*}
&d(x_1,x_2) = d(\phi(x_0),\phi(x_1)) &\leq \alpha d(x_0,x_1) \\
&d(x_2,x_3)=d(\phi(x_1),\phi(x_2)) \leq \alpha d(x_1,x_2) \leq \alpha (\alpha d(x_0,x_1)) &= \alpha^2 d(x_0,x_1)\\
&d(x_3,x_4) =d(\phi(x_2), \phi(x_3)) \leq \alpha d(x_2,x_3) \leq \alpha(\alpha^2d(x_0,x_1)) &= \alpha^3d(x_0,x_1)
\end{align*}

Por inducción sobre $n$ podemos concluir que la distancia entre cualquier punto de la sucesión y el siguiente está limitada por

\begin{equation}
d(x_n,x_{n+1})=d(x_n, \phi(x_n)) \leq \alpha^n d(x_0,x_1)
\end{equation}

Pasemos a probar que $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ es de Cauchy en $X.$

Sea $\varepsilon>0$ y $N \in \mathbb{N}$ tal que $N \geq \, \dfrac{ln \left(\dfrac{\varepsilon(1- \alpha)}{d(x_0,x_1)}\right)}{ln (\alpha)}.$ Entonces si $n > N:$

\begin{align*}
& &n &> \dfrac{ln \left(\dfrac{\varepsilon(1- \alpha)}{d(x_0,x_1)}\right)}{ln (\alpha)} \\
&\Rightarrow & n \, ln (\alpha) &< ln \left(\dfrac{\varepsilon(1- \alpha)}{d(x_0,x_1)}\right) \\
&\Rightarrow & ln (\alpha^n) &< ln \left(\dfrac{\varepsilon(1- \alpha)}{d(x_0,x_1)}\right) \\
&\Rightarrow & exp(ln (\alpha^n)) &< exp \left(ln \left(\dfrac{\varepsilon(1- \alpha)}{d(x_0,x_1)}\right) \right) \\
&\Rightarrow & \alpha^n &< \dfrac{\varepsilon(1- \alpha)}{d(x_0,x_1)}
\end{align*}

\begin{equation}
\Rightarrow \, \dfrac{\alpha^n}{1- \alpha} d(x_0,x_1) < \large{\varepsilon}
\end{equation}

Sean $n,m \in \mathbb{N} \,$ tales que $n,m > N.$ Sin pérdida de generalidad supón que $m \geq n.$ Entonces $m \, = \, n+p$ para algún $p \in \mathbb{N}.$ A partir de la desigualdad del triángulo sabemos que la distancia entre el punto $x_n$ y el punto $x_m=x_{n+p}$ es menor igual que la suma de las distancias de todos los puntos de la sucesión que están entre ellos dos.

Se sigue:

\begin{align*}
d(x_n,x_m) &= d(x_n,x_{n+p})\\
&\leq d(x_n,x_{n+1}) +d(x_{n+1},x_{n+2}) …+ d(x_{n+p-2},x_{n+p-1})+d(x_{n+p-1},x_{n+p})\\
&\leq \alpha^n d(x_0,x_1) +\alpha^{n+1} d(x_0,x_1)+…+ \alpha^{n+p-2} d(x_0,x_1)+\alpha^{n+p-1} d(x_0,x_1) \text{ por ec. $(1)$}\\
&= (\alpha^n +\alpha^{n+1} +…+ \alpha^{n+p-2} +\alpha^{n+p-1} ) \, d(x_0,x_1) \\
&=\alpha^n \, (1+\alpha +…+\alpha^{p-2}+\alpha^{p-1}) \, d(x_0,x_1)
\end{align*}

Nota que $1+\alpha +…+\alpha^{p-2}+\alpha^{p-1}$ es la suma de los primeros términos de la serie $\sum_{k=0}^{\infty}\, \alpha^k.$ Probablemente has visto en otros cursos que ésta es una serie convergente y que $\sum_{k=0}^{\infty}\, \alpha^k \, = \dfrac{1}{1-\alpha}$, pues $|\alpha|<1.$ Puedes consultarlo en la sección Cálculo Diferencial e Integral II: Series Geométricas. Entonces:

$$1+\alpha +…+\alpha^{p-2}+\alpha^{p-1} \leq \sum_{k=0}^{\infty}\, \alpha^k \, = \dfrac{1}{1-\alpha}$$

De modo que

\begin{align*}
\alpha^n \, (1+\alpha +…+\alpha^{p-2}+\alpha^{p-1}) \, d(x_0,x_1) &\leq \alpha^n \, \sum_{k=0}^{\infty}\, \alpha^k \, d(x_0,x_1) \\
&\leq \alpha^n \frac{1}{1- \alpha} \, d(x_0,x_1)\\
&< \varepsilon \text{ por ec. (2)}
\end{align*}

Por lo tanto $d(x_n,x_m) < \varepsilon \, $ lo cual demuestra que $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ es una sucesión de Cauchy.

Más adelante

Terminaremos con la prueba del teorema de punto fijo de Banach. Mostraremos condiciones bajo las cuales esta sucesión de Cauchy es convergente y cómo aproximar la sucesión al punto de convergencia.

Tarea moral

1. Da un ejemplo de un espacio métrico completo y una función $\phi: X \to X$ que satisface que para cada $x,y \in X$ con $x \neq y, \, d(\phi(x), \phi(y)) < d(x,y)$ y que no tiene ningún punto fijo.
2. Luego de conocer la Unidad 6 de compacidad, prueba que si $X$ es un espacio métrico compacto y $\phi: X \to X$ satisface que para cada $x,y \in X$ con $x \neq y, \, d(\phi(x), \phi(y)) < d(x,y)$ entonces $\phi$ tiene un único punto fijo.

Bibliografía

• Apostol, T., Análisis Matemático (2a ed.). México: Editorial Reverté, 1996. Págs: 111 y 112.
• Clapp, M., Análisis Matemático. Ciudad de México: Editorial Papirhos, IM-UNAM, 2013. Págs: 99-101 y 116.
• Jost, J., Postmodern Analysis (3rd ed.). New York: Springer-Verlag, 2005. Págs: 43 y 44.
• Kolmogorov, A.N., Fomin, S.V., Elementos de la Teoría de Funciones y del Análisis Funcional. (2a ed.). Moscú: Editorial MIR, 1975. Págs: 79 y 80.
• Rudin, W., Principles of Mathematical Analysis (3rd ed.). New York: McGraw–Hill, 1953. Págs: 220 y 221.

Enlaces

• Análisis Matemático.
• Guía de notación para Análisis Matemático I
• Enlace a entrada anterior.
• Enlace a entrada siguiente.

Introducción

Así como ya hicimos comparaciones de continuidad o diferenciabilidad del límite de una sucesión de funciones a partir de sus términos, en esta ocasión lo haremos con funciones integrables.

Partimos de una sucesión de funciones donde para cada $n \in \mathbb{N}, \, f_n:[a,b] \to \mathbb{R}, \, a,b \in \mathbb{R}.$ Supón además que $(f_n)_{n \in \mathbb{N}} \,$ converge puntualmente a una función $f$ en $[a,b].$

Si cada una de las funciones $f_n$ son integrables, ¿será $f$ también integrable?

¿La sucesión de integrales converge? ¿Su límite coincide con la integral del límite? Veamos el siguiente:

Ejemplo:

Considera el conjunto $\mathbb{Q} \cap [0,1].$ Como es numerable, podemos identificarlo como $\mathbb{Q} \cap [0,1] = \{ x_n: n \in \mathbb{N} \}.$ Para cada $n \in \mathbb{N}$ definimos $\mathcal{X}_{\{x_n\}}$ como la función característica dada por:

Ahora, para cada $n \in \mathbb{N}$ definimos $f_n := \mathcal{X}_{\{x_1\}}+…+\mathcal{X}_{\{x_n\}}.$

Entonces la función $f_n$ es integrable en $[a,b]$ y la sucesión $(f_n)_{n \in \mathbb{N}} \,$ converge puntualmente a la función:

\begin{equation*}
\mathcal{X}_{ \, \mathbb{Q} \cap [0,1]} := \begin{cases}
1 & \text{si $x \in \mathbb{Q} \cap [0,1]$} \\
0 & \text{si $x \notin\mathbb{Q} \cap [0,1]$}
\end{cases}
\end{equation*}

Pero $\mathcal{X}_{ \, \mathbb{Q} \cap [0,1]}$ no es integrable en $[0,1].$ Por lo tanto la convergencia puntual podría no bastar para que el límite sea integrable. ¿Y si la convergencia es uniforme?

Proposición. Sea $(f_n)_{n \in \mathbb{N}} \,$ una sucesión de funciones integrables en $[a,b]$ que converge uniformemente a una función $f$ en $[a,b].$ Entonces $f$ es integrable y
$$\int_{a}^{b} f = \underset{n \to \infty}{lim} \, \int_{a}^{b} f_n.$$

Demostración:
Para cada $n \in \mathbb{N}$ sea $\large{\varepsilon_n} := \underset{a \leq x \leq b}{sup}|f_n(x) – f(x)|.$
Entonces $f_n \, – \, \large{\varepsilon_n} \leq f \leq f_n + \varepsilon_n,$ de modo que las integrales superior e inferior de $f$ satisfacen:
$\int_{a}^{b} (f_n \, – \, \large{\varepsilon_n}) \, dx \leq \underline{\int} f \, dx\leq \overline{\int} f \, dx \leq \int_{a}^{b}(f_n + \large{\varepsilon_n}) \, dx$

Entonces $0 \leq \overline{\int} f \, dx – \underline{\int} f \, dx \leq \int_{a}^{b}(f_n + \large{\varepsilon_n}) \, dx – \int_{a}^{b} (f_n – \large{\varepsilon_n}) \, dx = 2\large{\varepsilon_n}[b-a].$
Dado que $\large{\varepsilon_n} \to 0$ porque $(f_n)_{n \in \mathbb{N}} \to f$ de manera uniforme, se sigue que $\overline{\int} f=\underline{\int} f.$ Por lo tanto $f$ es integrable.

Podemos ver también que
$\left| \int_{a}^{b} f \, dx \, – \, \int_{a}^{b} f_n \, dx \right| \leq \large{\varepsilon_n}[b-a] \to 0$ lo que demuestra que
$$\int_{a}^{b} f = \underset{n \to \infty}{lim} \, \int_{a}^{b} f_n.$$

Es importante mencionar que la convergencia uniforme no es una condición necesaria para que se de esta igualdad. Veamos el siguiente:

Ejemplo:

Para cada $n \in \mathbb{N}$ sea $f_n(x) = x^n$ con $x \in [0,1].$ En la entrada Convergencia uniforme y continuidad mostramos que la sucesión $(x^n)_{n \in \mathbb{N}} \, $ converge puntualmente a la función:

\begin{equation*}
f(x)= \begin{cases}
0 & \text{ si $0\leq x<1$}\\
1 & \text{ si $x=1$}
\end{cases}
\end{equation*}

Si calculamos las integrales tenemos que para cada $n \in \mathbb{N}:$

$\large{\int_{0}^{1}x^n} \, dx = \dfrac{1}{n+1} \to 0 = \large{\int_{0}^{1} f(x)} \, dx.$

Por lo tanto
$$ \int_{0}^{1}f(x) \, dx =\underset{n \to \infty}{lim} \, \int_{0}^{1}f_n(x) \, dx.$$

Las condiciones de este ejemplo pueden generalizarse. Antes conozcamos algunas definiciones:

Definición. Sucesión uniformemente acotada. Sea $(f_n)_{n \in \mathbb{N}} \,$ una sucesión de funciones con $f_n: A \subset \mathbb{R} \to \mathbb{R}, \, n \in \mathbb{N}. \,$ Diremos que es uniformemente acotada en $A$ si existe $M >0 \in \mathbb{R}$ tal que $|f_n(x)| \leq M$ para cualquier $x \in A$ y cualquier $n \in \mathbb{N}.$

Definición. Sucesión acotadamente convergente. Una sucesión de funciones $(f_n)_{n \in \mathbb{N}} \,$ con $f_n: A \subset \mathbb{R} \to \mathbb{R}, \, n \in \mathbb{N}$ es acotadamente convergente en $A$ si converge puntualmente y es uniformemente acotada en $A.$

Proposición. Sea $(f_n)_{n \in \mathbb{N}} \,$ una sucesión acotadamente convergente en $[a,b]$ donde cada función es integrable en $[a,b],$ y la función límite $f$ es integrable en $[a,b].$ Supongamos también que existe una partición $P$ de $[a,b],$ a saber, $P=\{x_0 = a,x_1,…,x_m=b\},$ tal que la sucesión $(f_n)_{n \in \mathbb{N}} \,$ es uniformemente convergente hacia $f$ en cada subintervalo $[c,d] \subset [a,b]$ que no contenga ninguno de los puntos $x_k \in P.$ Entonces:

$$ \underset{n \to \infty}{lim} \, \int_{a}^{b} f_n(x) \, dx = \int_{a}^{b} f(x) \, dx.$$

Demostración:
Dado que $f$ es acotada y $(f_n)_{n \in \mathbb{N}} \,$ es uniformemente acotada, existe $M >0$ tal que $|f_n(x)| \leq M$ para cada $x \in [a,b]$ y para cualquier $n \in \mathbb{N}.$
Sea $\varepsilon > 0$ tal que $2 \varepsilon < \norm{P},$
sea $h = \frac{\varepsilon}{2m},$ donde $m$ es el número de subintervalos de $P,$
considera una nueva partición $P’$ de $[a,b]$ dada por:
$P’=\{x_0, \, x_0+h,\, x_1-h,\, x_1+h, \, … \, ,x_{m-1}-h, \, x_{m-1}+h, \, x_m-h, \, x_m\}$

Nota que la función $|f-f_n|$ es integrable en $[a,b]$ y es acotada por $2M.$ Consideremos la integral de esta función en cada uno de los intervalos de la nueva partición $P’.$

Por un lado, consideremos la suma de las integrales de $|f-f_n|$ tomadas sobre los intervalos que sí tienen algún punto de $P,$ es decir los intervalos
$[x_0,x_0+h], \, [x_1-h,x_1+h],…,[x_{m-1}-h,x_{m-1}+h], \, [x_m-h,x_m].$

La suma está dada por:

\begin{align*}
&\int_{x_0}^{x_0+h} |f-f_n|(x)\, dx + \int_{x_1-h}^{x_1+h} |f-f_n|(x)\, dx +…+ \int_{x_{m-1}-h}^{x_{m-1}+h} |f-f_n|(x)\, dx + \int_{x_m-h}^{x_m} |f-f_n|(x)\, dx \\
\leq & 2M(x_0+h-x_0) + 2M(x_1+h-(x_1-h))+…+2M(x_{m-1}+h-(x_{m-1}-h))+2M(x_m-(x_m-h)) \\
=&2Mh+2M(2h)+…+2M(2h)+2Mh \\
=&2M(2hm) \\
=&2M \varepsilon
\end{align*}

El subconjunto restante de $[a,b]$ lo llamaremos $S.$ Está formado por un número finito de intervalos cerrados en los que $(f_n)_{n \in \mathbb{N}} \,$ converge uniformemente hacia $f$ (pues no tiene ningún punto de $P$). Por consiguiente, existe $N \in \mathbb{N}$ tal que para cada $x \in S,$ si $n \geq N \,$ se cumple que
$$|f(x)-f_n(x)| < \varepsilon$$

De modo que la suma de las integrales de $|f-f_n|$ sobre los intervalos de $S$ es a lo sumo $\large{\varepsilon} (b-a),$ luego para cada $n \geq N:$

$\int_{a}^{b}|f(x)-f_n(x)|dx \leq (2M + b-a) \large{\varepsilon} \, \to \, 0.$

Esto demuestra que $\int_{a}^{b}f_n(x)dx \to \int_{a}^{b}f(x)dx$ cuando $n \to \infty .$

En la última sección de Análisis Matemático I hablaremos de la integral de Riemann-Stieltjes, que es un concepto que generaliza la integral de Riemann. La proposición vista aquí se puede expresar como sigue:

Proposición. Sucesión de funciones Riemann-Stieltjes: Sea $\alpha$ monótona en $[a,b].$ Supón que para cada $n \in \mathbb{N}, \, f_n \in \mathcal{R}(\alpha)$ en $[a,b].$ Si $(f_n)_{n \in \mathbb{N}} \,$ converge uniformemente a $f$ en $[a,b]$ entonces $f \in \mathcal{R}(\alpha)$ en $[a,b]$ y:

$$\int_{a}^{b} f \, d \alpha = \underset{n \to \infty}{lim} \, \int_{a}^{b} f_n \, d \alpha .$$

Más adelante…

Hablaremos de series de funciones y del límite de ellas. Así conoceremos el concepto de convergencia uniforme pero ahora en sumas infinitas.

Tarea moral

1. Sea $f_n$ como en el primer ejemplo. Prueba que en efecto la sucesión $(f_n)_{n \in \mathbb{N}} \,$ no converge uniformemente a la función:
   \begin{equation*}
   \mathcal{X}_{ \, \mathbb{Q} \cap [0,1]} = \begin{cases}
   1 & \text{si $x \in \mathbb{Q} \cap [0,1]$} \\
   0 & \text{si $x \notin\mathbb{Q} \cap [0,1]$}
   \end{cases}
   \end{equation*}
2. Sea $(f_n)_{n \in \mathbb{N}} \,$ una sucesión de funciones acotadas con $f_n: A \subset \mathbb{R} \to \mathbb{R}, \, n \in \mathbb{N}, \,$ tal que converge uniformemente a una función $f:A \to \mathbb{R}.$ Demuestra que $(f_n)_{n \in \mathbb{N}} \,$ es uniformemente acotada en $A.$
3. Regresa luego de ver la integral de Riemann-Stieltjes y demuestra la última proposición de esta sección.

Bibliografía

• Apostol, T., Análisis Matemático (2a ed.). México: Editorial Reverté, 1996. Págs: 275-278.
• Rudin, W., Principles of Mathematical Analysis (3rd ed.). New York: McGraw–Hill, 1953. Págs: 151 y 152.

Enlaces

• Análisis Matemático.
• Guía de notación para Análisis Matemático I
• Enlace a entrada anterior.
• Enlace a entrada siguiente.

Introducción

Cuando los puntos de un espacio métrico son enviados al mismo espacio a través de una función, conviene saber si habrá algún punto que se envíe a sí mismo, es decir, que se conserve fijo. Las próximas entradas nos mostrarán cuándo esa situación ocurre y resultados interesantes derivados de ello. Comencemos con la primera:

Definición. Función contracción. Sea $(X,d)$ un espacio métrico y $ \phi: X \to X$ una función. Diremos que $\phi$ es una contracción si existe $\alpha \in (0,1)$ tal que para cualesquiera $x,y \in X$ se cumple que:
$$d(\phi(x),\phi(y)) \leq \alpha \, d(x,y)$$

Podemos pensar entonces, que una función contracción, justamente hace que los puntos sean más cercanos entre sí de lo que eran originalmente.

Nota que una contracción es también una función Lipschitz continua con constante de Lipschitz $c<1.$ Este concepto se vio en la entrada Más conceptos de continuidad. Demos paso a otra:

Definición. Punto fijo. Sea $X$ un espacio métrico y $x^* \in X.$ Decimos que $x^*$ es punto fijo de la función $\phi:X \to X$ si $\phi(x^*)=x^*.$

Para ejemplificar estas ideas, veamos dos funciones que son contracciones y cómo existe un punto fijo en los casos a mencionar:

Ejemplo: $f(x)=\dfrac{x}{2},$ con $\alpha = \dfrac{1}{2}.$

Considera $f: \mathbb{R} \to \mathbb{R}$ tal que $f(x)=\dfrac{x}{2}$ en el espacio euclidiano. Sean $x,y \in \mathbb{R}.$ Sucede que:

\begin{align*}
d(f(x),f(y))&=|f(x)-f(y)| \\
&=\left|\frac{x}{2}-\frac{y}{2} \right| \\
&=\left|\frac{1}{2}(x-y) \right| \\
&=\frac{1}{2}|x-y| \\
&=\frac{1}{2}d(x,y)
\end{align*}

Por lo tanto $d(f(x),f(y)) \leq \frac{1}{2}d(x,y)$ lo que demuestra que $f$ es una contracción con $\alpha = \frac{1}{2}.$

La siguiente imagen representa la diferencia de las distancias antes y después de aplicar la función en dos puntos $x$ y $y.$ Basta con observar las proyecciones de la gráfica de $f$ en los ejes coordenados.

Ahora busquemos un punto fijo:

\begin{align*}
f(x)&=x \\
\iff \frac{x}{2}&=x \\
\iff x&=2x \\
\iff 0&=2x-x \\
\iff 0&=x
\end{align*}

Es decir, $0$ es el único punto fijo de $f.$

A continuación, vamos a construir una sucesión de la siguiente manera:

Toma cualquier $x_0 \in X$

$x_1:=f(x_0)=\dfrac{x_0}{2}$

$x_2 :=f(x_1)=\dfrac{\dfrac{x_0}{2}}{2}=\dfrac{x_0}{2^2}$

$x_3:=f(x_2)=\dfrac{\dfrac{x_0}{2^2}}{2}=\dfrac{x_0}{2^3}$
.
.
.
$x_k:=f(x_{k-1})=\dfrac{x_0}{2^k}$

Entonces la sucesión se define como $(x_n)_{n \in \mathbb{N}} \, $ donde $x_n = \dfrac{x_0}{2^n}.$
Nota que tiende a $0$ en $\mathbb{R}.$

En las siguientes gráficas podemos observar el comportamiento de la sucesión:

Sea $x_0 \in X.$ Mostramos la gráfica de la función $f(x)=\dfrac{x}{2}$ y la función identidad $ \, \mathcal{I}(x)=x.$
Señalamos los términos $x_0$ y $x_1 :=f(x_0)=\dfrac{x_0}{2}$ y la distancia entre $f(x_0) \,$ y $\, f(x_1)$ vistos como proyecciones de las gráficas de los puntos sobre los ejes del plano cartesiano:

Si continuamos, generamos el punto $x_2=f(x_1).$ Gráficamente también es visible que las distancias entre dos puntos disminuyen en el eje vertical al continuar con las iteraciones.

Podemos observar que los puntos convergen a $0$ que recordemos, es también el punto fijo de $f.$

Veamos otro caso:

Ejemplo: $f(x)=\dfrac{x}{2}+6,$ con $\alpha = \dfrac{1}{2}.$

Considera $f: \mathbb{R} \to \mathbb{R}$ tal que $f(x)=\dfrac{x}{2}+6$ en el espacio euclidiano. Sean $x,y \in \mathbb{R}.$ Sucede que:

\begin{align*}
|f(x)-f(y)|&=\left|\frac{x}{2}+6- \left(\frac{y}{2}+6 \right) \right| \\
&= \left|\frac{1}{2}(x-y) \right| \\
&= \frac{1}{2}|x-y|
\end{align*}

De modo que $d(f(x),f(y))\leq \frac{1}{2}d(x,y)$ lo cual prueba que $f$ es una contracción con $\alpha = \frac{1}{2}.$

Busquemos puntos fijos:

\begin{align*}
&f(x)&=x \\
\iff &\frac{x}{2}+6 &=x \\
\iff &6 &\, = \frac{x}{2} \\
\iff &12 & = x
\end{align*}

Entonces $12$ es el único punto fijo de $f.$

El siguiente gráfico nos confirma estos resultados para la sucesión generada a partir de un punto $x_0 \in X$ donde para cada $n \in \mathbb{N}, \, x_n=f(x_{n-1}).$

Queda como ejercicio al lector demostrar que $(x_n)_{n \in \mathbb{N}} \to 12$ en $\mathbb{R}.$

Esto da pie para enunciar el:

Teorema de punto fijo de Banach. Sea $(X,d)$ un espacio métrico completo y sea $\phi:X \to X$ una contracción, entonces:

1. Para cada $x_0 \in X$ la sucesión $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ es de Cauchy y, en consecuencia $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ converge a un punto $x^* \in X.$ $\, \phi^n$ representa la composición $\, \underset{n \, veces}{\underbrace{ \phi \circ … \circ \phi }}$
2. El punto $x^*$ descrito es punto fijo de $\phi.$
3. El punto fijo es único.
4. Podemos estimar la distancia de $\phi ^n(x_0)$ a $x^*$ usando la desigualdad:
   $$d( \phi ^n(x_0),x^*) \leq \frac{\alpha^n}{1-\alpha} \, d( x_0, \phi (x_0)).$$

Por lo pronto demostremos que si una contracción tiene un punto fijo entonces este es único.

Sean $x, y \in X$ tales que $\phi(x)=x \,$ y $\, \phi(y)=y.$ Como $\phi$ es una contracción se tiene que:

$$d(x,y) = d(\phi(x),\phi(y)) \leq \alpha d(x,y) $$

Como $\alpha <1$ se sigue que:
$$\alpha d(x,y) \leq d(x,y)$$
Por lo tanto $d(x,y)=d(x,y),$ y en consecuencia $x=y.$

Más adelante…

Continuaremos con la demostración del teorema de punto fijo de Banach. En la siguiente entrada comprobaremos que la sucesión $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ es de Cauchy.

Tarea moral

1. Sea $f: \mathbb{R} \to \mathbb{R}$ tal que $f(x) := \dfrac{x}{2} +6$ en el espacio euclidiano. Sea $x_0 \in \mathbb{R}, \,$ prueba que la sucesión $(f^n(x_0))_{n \in \mathbb{N}} \, $ converge a $12.$
2. Sea $f:[a,b] \to [a,b], \, a,b \in \mathbb{R} \,$ una función continua. Demuestra que tiene al menos un punto fijo.
3. Da un ejemplo de una función continua $f:[a,b] \to [a,b], \, a,b \in \mathbb{R} \,$ con una infinidad de puntos fijos.
4. Prueba que si $f: \mathbb{R} \to \mathbb{R}$ y para cada $x \in \mathbb{R}, \, |f'(x)| \leq M<1$ entonces $f$ es una contracción.
5. Da un ejemplo de un espacio métrico completo y una función $\phi: X \to X \,$ que satisface que para todo $x \neq y \in X, \, d(\phi(x), \phi(y)) < d(x,y)$ pero que no tenga ningún punto fijo.

Bibliografía

• Apostol, T., Análisis Matemático (2a ed.). México: Editorial Reverté, 1996. Págs: 111 y 112.
• Clapp, M., Análisis Matemático. Ciudad de México: Editorial Papirhos, IM-UNAM, 2013. Págs: 99-101 y 116.
• Jost, J., Postmodern Analysis (3rd ed.). New York: Springer-Verlag, 2005. Págs: 43 y 44.
• Kolmogorov, A.N., Fomin, S.V., Elementos de la Teoría de Funciones y del Análisis Funcional. (2a ed.). Moscú: Editorial MIR, 1975. Págs: 79 y 80.
• Rudin, W., Principles of Mathematical Analysis (3rd ed.). New York: McGraw–Hill, 1953. Pág: 220.

Enlaces

• Análisis Matemático.
• Guía de notación para Análisis Matemático I
• Enlace a entrada anterior.
• Enlace a entrada siguiente.

Introducción

En la entrada anterior vimos que cuando una sucesión de funciones continuas converge uniformemente, podemos concluir que el límite es también una función continua. ¿Qué ocurrirá con funciones diferenciables?

Considera el espacio de funciones con dominio en $[a,b]$ con $a,b$ e imagen en $\mathbb{R}.$ Tal vez intuimos que si tenemos una sucesión de funciones diferenciables $(f_n)_{n \in \mathbb{N}} \,$ que convergen uniformemente a una función $f$ en $[a,b]$ entonces $f$ también es diferenciable y la sucesión de derivadas $(f’_n)_{n \in \mathbb{N}} \,$ converge uniformemente en $f’.$ Esto es falso, como muestra el siguiente:

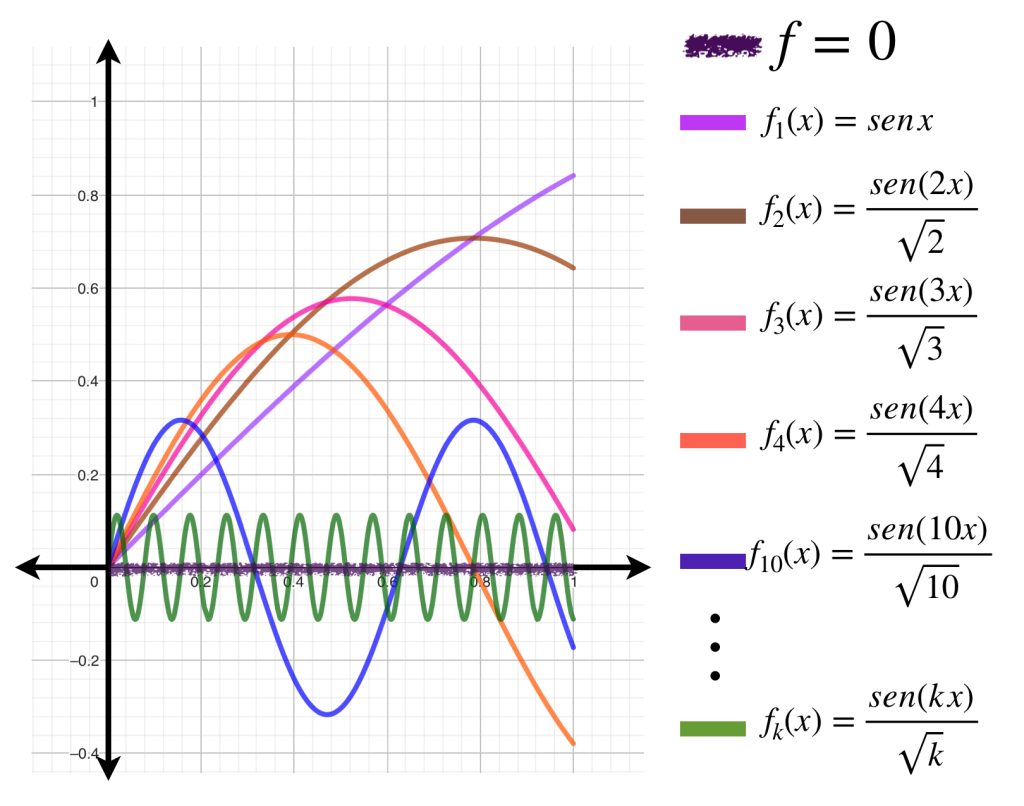
Ejemplo. La sucesión $\left( \dfrac{sen (nx)}{\sqrt{n}} \right) _{n \in \mathbb{N}} \,$

Para cada $n \in \mathbb{N}$ sea $f_n:[0,1] \to \mathbb{R} \,$ tal que $f_n(x)=\dfrac{sen (nx)}{\sqrt{n}}.$ Ocurre que $\left( \dfrac{sen (nx)}{\sqrt{n}} \right) _{n \in \mathbb{N}} \,$ converge uniformemente a la función $f(x)=0.$

Esto es porque, para cualquier $x \in [0,1], \, |sen(nx)|<1.$ Por otro lado, $\sqrt{n} \to \infty.$ Por lo tanto $\left|\dfrac{sen (nx)}{\sqrt{n}} \right| = \dfrac{|sen(nx)|}{\sqrt{n}} \leq \dfrac{1}{\sqrt{n}} \to 0.$

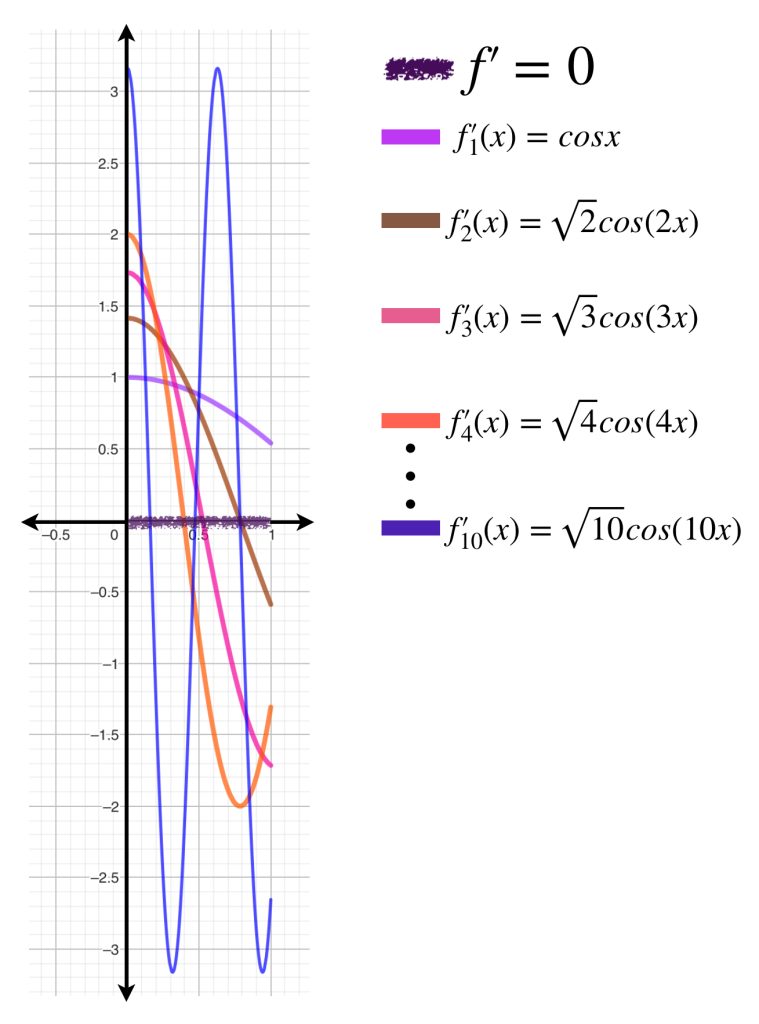
Por otro lado, para cada $n \in \mathbb{N}$ se tiene que $f'(x)= \sqrt{n} \, cos(nx).$ Pero $(f’_n)_{n \in \mathbb{N}} \,$ no converge a $f’$ ni de forma puntual. Por ejemplo $f’_n(0)=\sqrt{n}$ tiende a $\infty$ mientras que $f'(0)=0.$

Ejemplo. La sucesión $\left( \dfrac{x}{1 + n x^2} \right) _{n \in \mathbb{N}} \,$

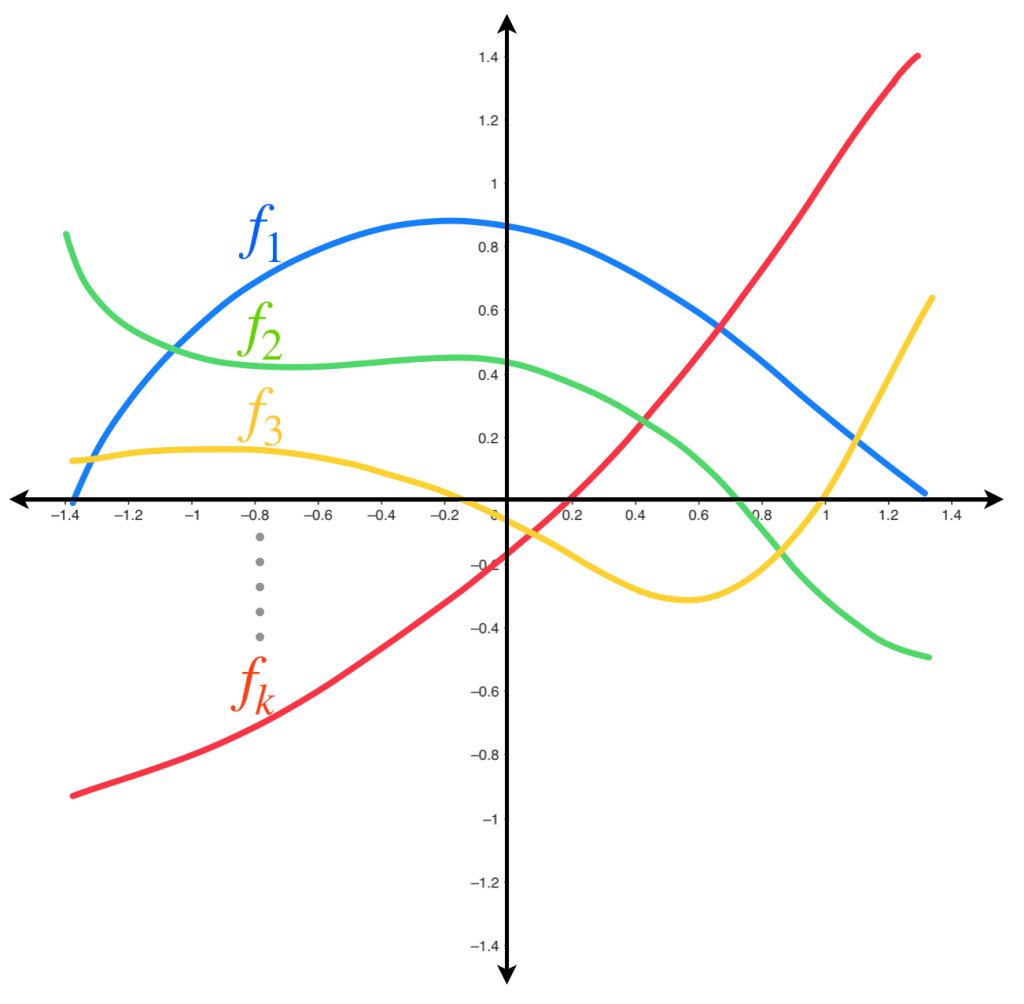
Para cada $n \in \mathbb{N}$ sea $f_n:\mathbb{R} \to \mathbb{R}$ tal que $f_n(x)=\dfrac{x}{1 + n x^2}.$

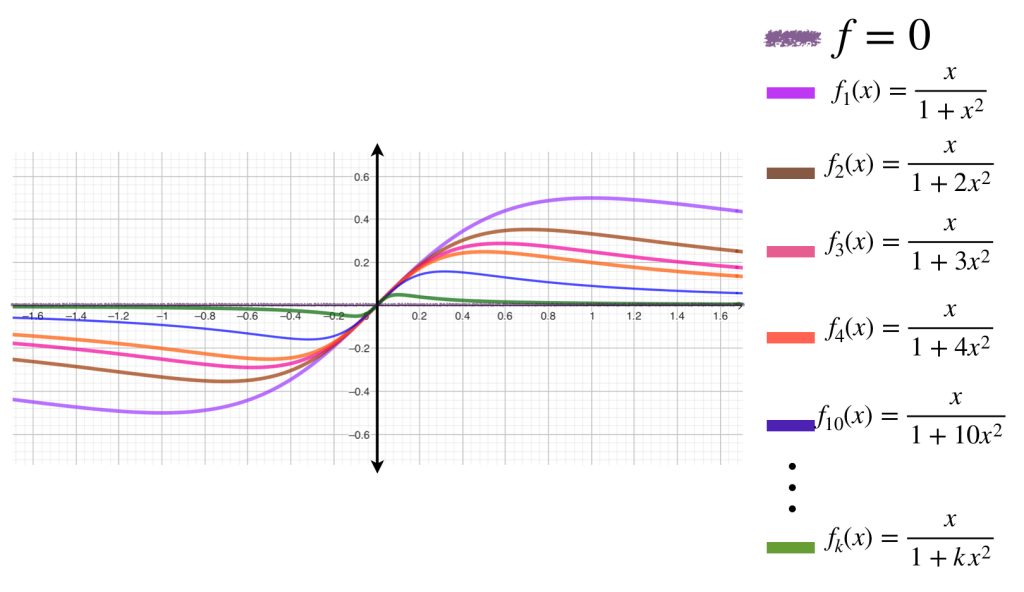
Comencemos identificando la función límite $f$ de la sucesión $(f_n)_{n \in \mathbb{N}} \,$ y la función límite $g$ de la sucesión de derivadas $(f’_n)_{n \in \mathbb{N}}.$

Ya la imagen anterior nos induce a proponer $f=0.$ También podemos observar que cada función tiene máximo y mínimo global cuya distancia a $0$ coincide. Además, estos se van acercando más al eje horizontal a medida que avanzamos en las funciones de la sucesión.

En efecto, cuando la derivada es $0,$ la función $f_n$ alcanza su máximo o mínimo global:
$$\dfrac{1-nx^2}{(nx^2+1)^2}=0 \, \iff \, 1-nx^2 = 0 \, \iff \, x = \pm \sqrt{\frac{1}{n}}$$

Esto significa que cada $f_n$ está acotada como sigue:
$|f_n(x)|= \left| \dfrac{x}{1 + n x^2} \right| \leq \left|\dfrac{\sqrt{\frac{1}{n}}}{1 + n \sqrt{\frac{1}{n}}^2}\right| = \dfrac{1}{2\sqrt{n}} \, \to \, 0.$

Lo cual prueba que $(f_n)_{n \in \mathbb{N}} \,$ converge uniformemente a $0.$

Para el límite de la sucesión de derivadas veamos la siguiente imagen.

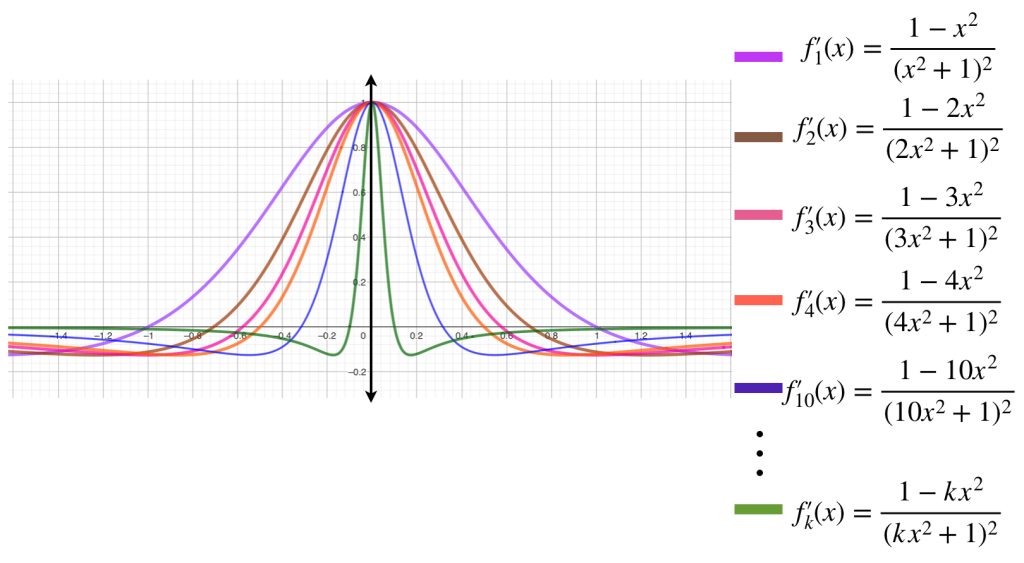
Esto incentiva proponer $g \,$ (la función a la que las gráficas de las derivadas parecen converger) como:

\begin{equation*}
g(x) = \begin{cases}
0 & \text{si x $\neq$ 0} \\
1 & \text{si $x = 0$}
\end{cases}
\end{equation*}

Entonces $f’$ no coincide con $g,$ pues asignan valores diferentes al ser evaluadas en $0.$ Dejaremos como ejercicio lo siguiente:

1. Probar que $(f’_n)_{n \in \mathbb{N}} \to g.$ ¿La convergencia es puntual o uniforme?
2. Identifica para qué valores de $x \in \mathbb{R}$ sí se cumple que $f'(x)=g(x).$
3. ¿En qué intervalos de $\mathbb{R}$ se da la convergencia uniforme de $(f_n)_{n \in \mathbb{N}} \,$ en $f.$
4. ¿En qué intervalos de $\mathbb{R}$ se da la convergencia uniforme de $(f’_n)_{n \in \mathbb{N}} \,$ en $g.$

Ejemplo. La sucesión $\left( \dfrac{1}{n} \, e^{-n^2x^2} \right) _{n \in \mathbb{N}} \,$

Para cada $n \in \mathbb{N}$ sea $f_n:\mathbb{R} \to \mathbb{R}$ tal que $f_n(x)=\dfrac{1}{n} \, e^{-n^2x^2}.$

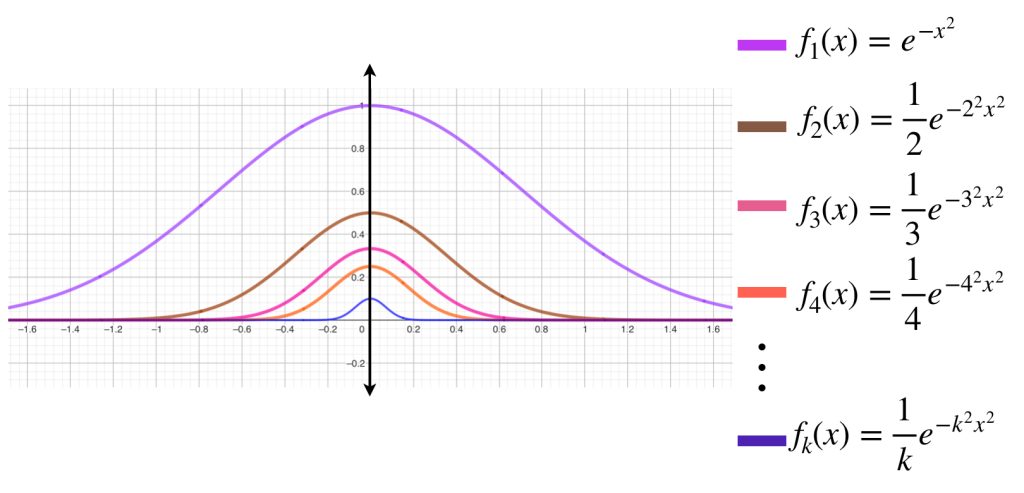
Veamos que $(f_n)_{n \in \mathbb{N}} \,$ converge uniformemente en $\mathbb{R}$ a la función $f=0.$

Para cada $n \in \mathbb{N}$ y para cada $x \in \mathbb{R}, \, f'(x)= -2nxe^{-n^2x^2}.$ Se puede demostrar que esta función alcanza su máximo global cuando $f'(x)=0, \,$ lo cual ocurre cuando $x=0.$ Entonces el máximo de $f_n$ está dado por $f(0)= \frac{1}{n} \, \to \, 0.$ Por lo tanto $(f_n)_{n \in \mathbb{N}} \,$ converge uniformemente en $\mathbb{R}$ a la función $f=0.$

Ahora observemos la sucesión de derivadas $(f’_n)_{n \in \mathbb{N}}.$

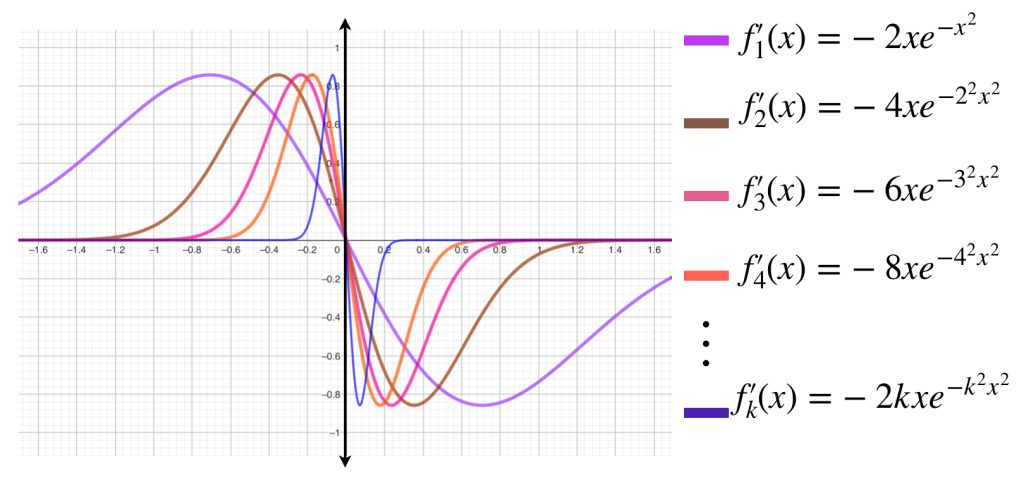
Dejamos como ejercicio al lector probar que $(f’_n)_{n \in \mathbb{N}} \,$ converge puntualmente a la función $g=0.$ No obstante, esta convergencia no es uniforme en ningún intervalo que contenga al origen.

Habiendo visto estas situaciones, conozcamos algunas condiciones de convergencia para $(f_n)_{n \in \mathbb{N}} \,$ y para $(f’_n)_{n \in \mathbb{N}} \,$ que implican que $f’ =g.$

Proposición. Para cada $n \in \mathbb{N}$ sea $f_n:[a,b] \to \mathbb{R}$ continuamente diferenciable en $[a,b],$ tal que la sucesión $(f_n)_{n \in \mathbb{N}} \,$ converge puntualmente a $f:[a,b] \to \mathbb{R}$ y la sucesión de derivadas $(f’_n)_{n \in \mathbb{N}} \,$ converge uniformemente a $g:[a,b] \to \mathbb{R}.$ Entonces $f$ es continuamente diferenciable en $[a,b]$ y $f’=g.$

Demostración:
Sean $j,k \in \mathbb{N}$ y $x_0 \in (a,b).$ La función $f_j-f_k$ es diferenciable en $[a,b],$ particularmente, para cada $x \in (a,b),$ también lo será en el intervalo $(x_0,x)$ (o $(x,x_0)$ dependiendo del orden de los puntos). Según el teorema del valor medio, que se puede consultar en Cálculo Diferencial e Integral I: Teorema de Rolle y teorema del valor medio, existe $\xi_x \in (x_0,x)$ tal que:

$$\frac{(f_j-f_k)(x)-(f_j-f_k)(x_0)}{x-x_0}=(f’_j-f’_k)(\xi_x)$$

Entonces
$$(f_j-f_k)(x)-(f_j-f_k)(x_0)=((f’_j-f’_k)(\xi_x))(x-x_0)$$
Y si desarrollamos vemos que
$$f_j(x)-f_j(x_0)-f_k(x)+f_k(x_0)=(f’_j(\xi_x)-f’_k(\xi_x))(x-x_0)$$
Así
\begin{align*}
|f_j(x)-f_j(x_0)-f_k(x)+f_k(x_0)|&=|(f’_j(\xi_x)-f’_k(\xi_x))(x-x_0)| \\
& \leq \norm{f’_j-f’_k}_\infty |x-x_0|
\end{align*}

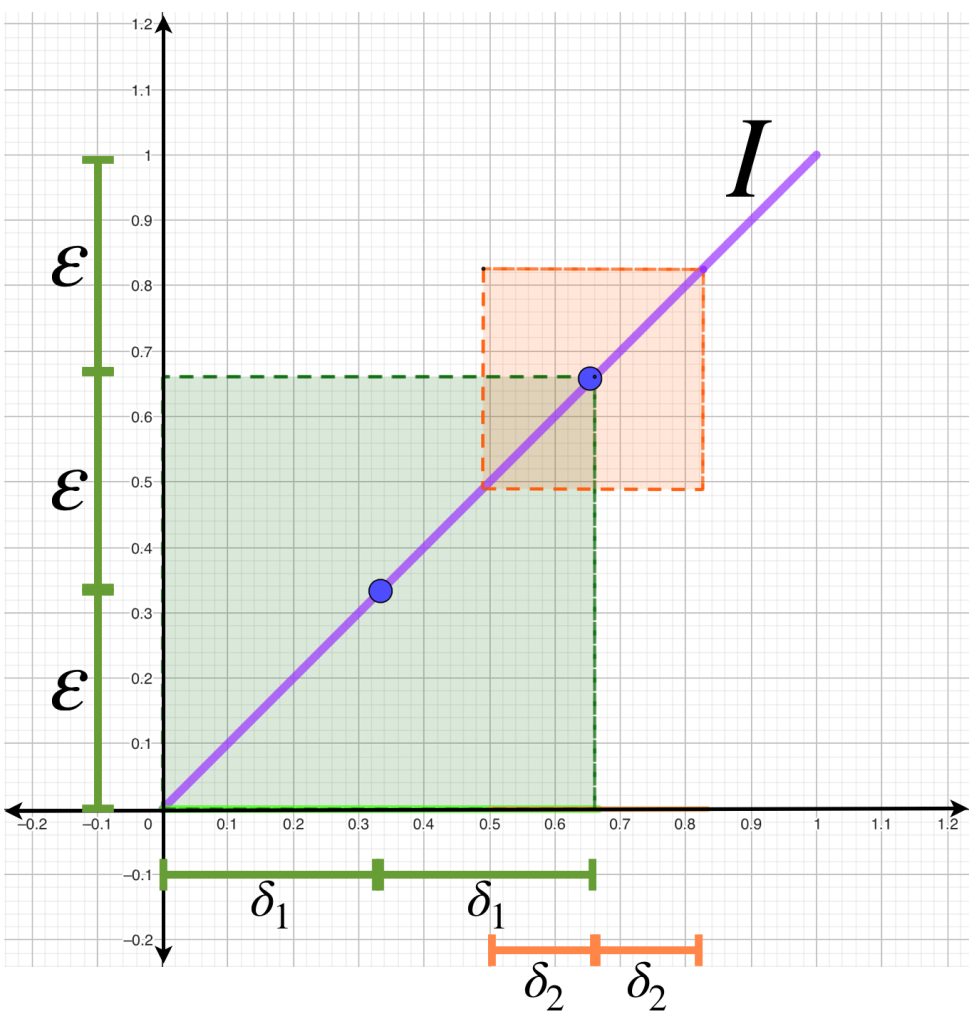
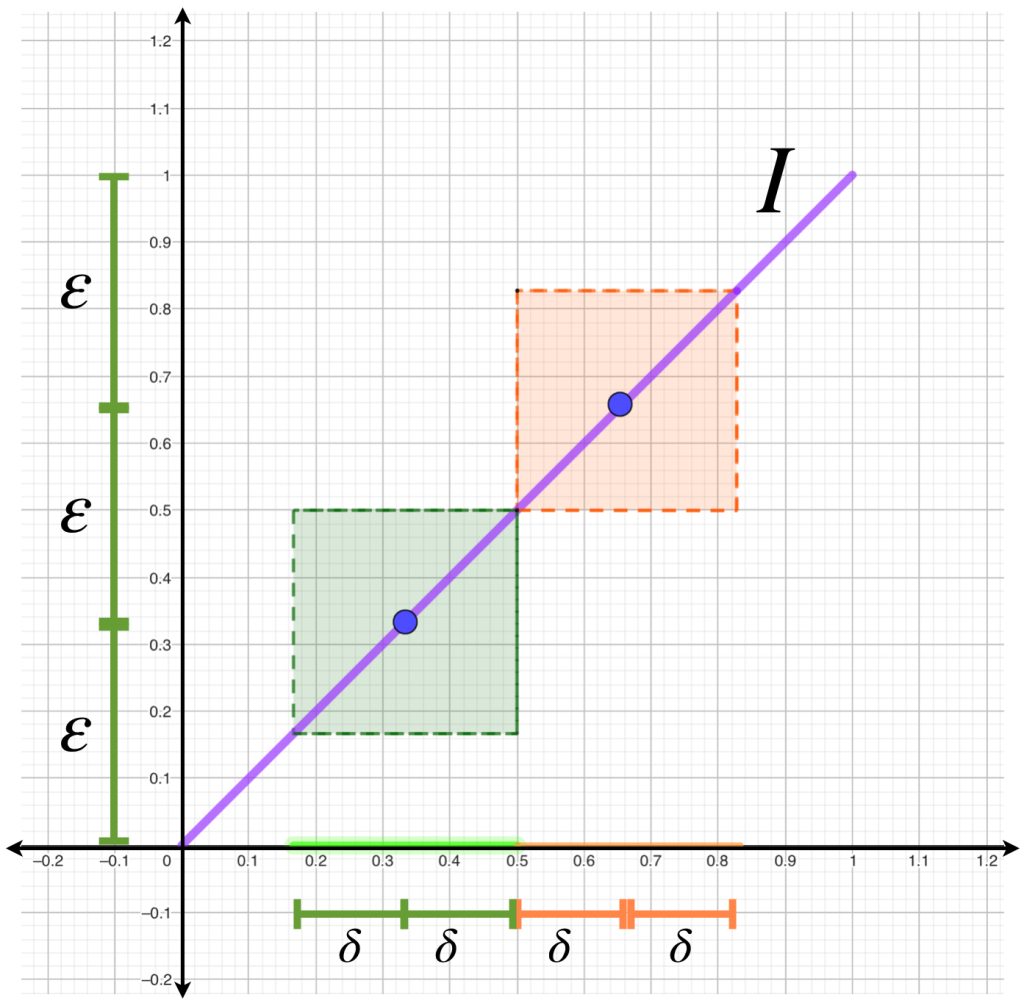
Dado que $(f’_n)_{n \in \mathbb{N}} \,$ converge uniformemente en $\mathcal{C}^0[a,b],$ para cada $\varepsilon >0$ existe $N_1 \in \mathbb{N}$ tal que para cada $x \in (a,b)$ y para cada $j,k \geq N_1:$

\begin{align*}
|f_j(x)-f_j(x_0)-f_k(x)+f_k(x_0)|& \leq \norm{f’_j-f’_k}_\infty |x-x_0| \\
& < \frac{\varepsilon}{3}|x-x_0|.
\end{align*}
Haciendo $j \to \infty$ se sigue que
$$|f(x)-f(x_0)-f_k(x)+f_k(x_0)|< \frac{\varepsilon}{3}|x-x_0|.$$

Por otro lado, como $(f’_n(x_0))_{n \in \mathbb{N}} \to g(x_0)$ existe $N_2 \in \mathbb{N}$ tal que para cada $k \geq N_1, \, |f’_k(x_0) – g(x_0)|< \frac{\varepsilon}{3}$

Sea $N= máx \{ N_1,N_2 \}.$ Existe $\delta >0$ tal que si $|x – x_0| < \delta$ entonces
$$\left| \frac{f_N(x)-f_N(x_0)}{x-x_0}-f’_N(x_0) \right| <\frac{\varepsilon}{3}.$$

Finalmente aplicamos la desigualdad de triángulo para concluir que
\begin{align*}
\left| \frac{f(x)-f(x_0)}{x-x_0}-g(x_0) \right| &\leq \left| \frac{f(x)-f(x_0)}{x-x_0} – \frac{f_N(x)-f_N(x_0)}{x-x_0} \right| + \left| \frac{f_N(x)-f_N(x_0)}{x-x_0}-f’_N(x_0) \right|+ |f’_N(x_0) – g(x_0)|\\
&< \frac{\varepsilon}{3}+\frac{\varepsilon}{3}+\frac{\varepsilon}{3}\\
&= \varepsilon
\end{align*}

Por lo tanto $f$ es diferenciable en $x_0$ y $f'(x_0)=g(x_0).$ Ya que las derivadas $f’_n$ son continuas y convergen uniformemente se sigue por lo visto en la entrada anterior que $f$ es continuamente diferenciable.

Hay un resultado más fuerte sobre convergencia uniforme y diferenciación. La prueba de este se omite pero puede consultarse en Apostol, T., Análisis Matemático (2a ed.). México: Editorial Reverté, 1996. Pag 278. Se enuncia como sigue:

Proposición. Para cada $n \in \mathbb{N}$ sea $f_n:(a,b) \to \mathbb{R}.$ Supongamos que para un punto $x_0 \in (a,b)$ la sucesión $(f_n(x_0))_{n \in \mathbb{N}} \,$ converge. Supongamos además que la sucesión de derivadas $(f’_n)_{n \in \mathbb{N}} \,$ converge uniformemente en $(a,b)$ a una función $g.$ Entonces la sucesión $(f_n)_{n \in \mathbb{N}} \,$ converge uniformemente en $(a,b)$ a una función $f$ derivable en $(a,b)$ y $f’=g.$

Más adelante…

Conoceremos la relación entre una sucesión de funciones integrables con su función límite. ¿Bajo qué condiciones será también integrable?

Tarea moral

1. Resuelve las actividades que quedaron pendientes en los ejemplos de esta entrada.

Bibliografía

• Apostol, T., Análisis Matemático (2a ed.). México: Editorial Reverté, 1996. Págs: 268, 278-280 y 303.
• Clapp, M., Análisis Matemático. Ciudad de México: Editorial Papirhos, IM-UNAM, 2013. Pág: 83.
• Rudin, W., Principles of Mathematical Analysis (3rd ed.). New York: McGraw–Hill, 1953. Págs: 152-153.

Enlaces

• Análisis Matemático.
• Guía de notación para Análisis Matemático I
• Enlace a entrada anterior.
• Enlace a entrada siguiente.