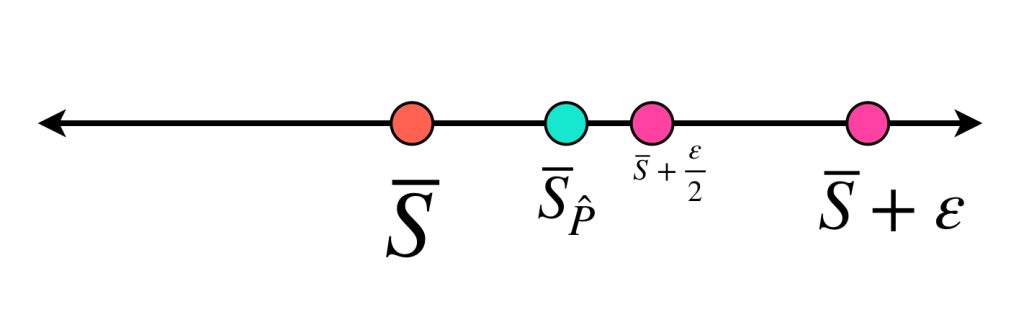$\textit{MATERIAL EN REVISIÓN}$
Introducción
El contenido de esta sección se basa predominantemente en el libro
Wheeden, R.L., Zygmund, A., Measure and Integral. An Introduccion to Real Analysis. (2da ed.). New York: Marcel Dekker, 2015, págs 34-37.
En la entrada anterior vimos que para cualesquiera $P_1, P_2 \in \mathcal{P}_{[a,b]}$ se cumple que $\underline{S}_{P_1} \leq \overline{S}_{P_2},$ entonces
\begin{align}
-\infty < \underset{P \in \mathcal{P}_{[a,b]}}{\text{sup} \, \underline{S}_P} \leq \underset{P \in \mathcal{P}_{[a,b]}}{\text{ínf} \, \overline{S}_P} < \infty.
\end{align}
Esto también ocurre con la integral de Riemann que se estudia en los cursos de Cálculo, donde además, cuando se da la igualdad $\, \underset{P \in \mathcal{P}_{[a,b]}}{\text{sup} \, \underline{S}_P} = \underset{P \in \mathcal{P}_{[a,b]}}{\text{ínf} \, \overline{S}_P} \, $ se toma el valor del límite como el valor de la integral. (Ver Cálculo Diferencial e Integral II: Definición de la integral definida).
Nota que nosotros no hemos definido así la integral de Riemann-Stieltjes, sino tomando particiones cuyas normas tienden a cero. Aunque la intuición nos dice que particiones de intervalos muy pequeños se aproximan demasiado al valor de la integral, esto no siempre ocurre. Específicamente, incluso cuando se cumple que $\, \underset{P \in \mathcal{P}_{[a,b]}}{\text{sup} \, \underline{S}_P} = \underset{P \in \mathcal{P}_{[a,b]}}{\text{ínf} \, \overline{S}_P} \,$ en el caso de las sumas inferior y superior de Riemann-Stieltjes, la integral podría no existir. Veamos un ejemplo.
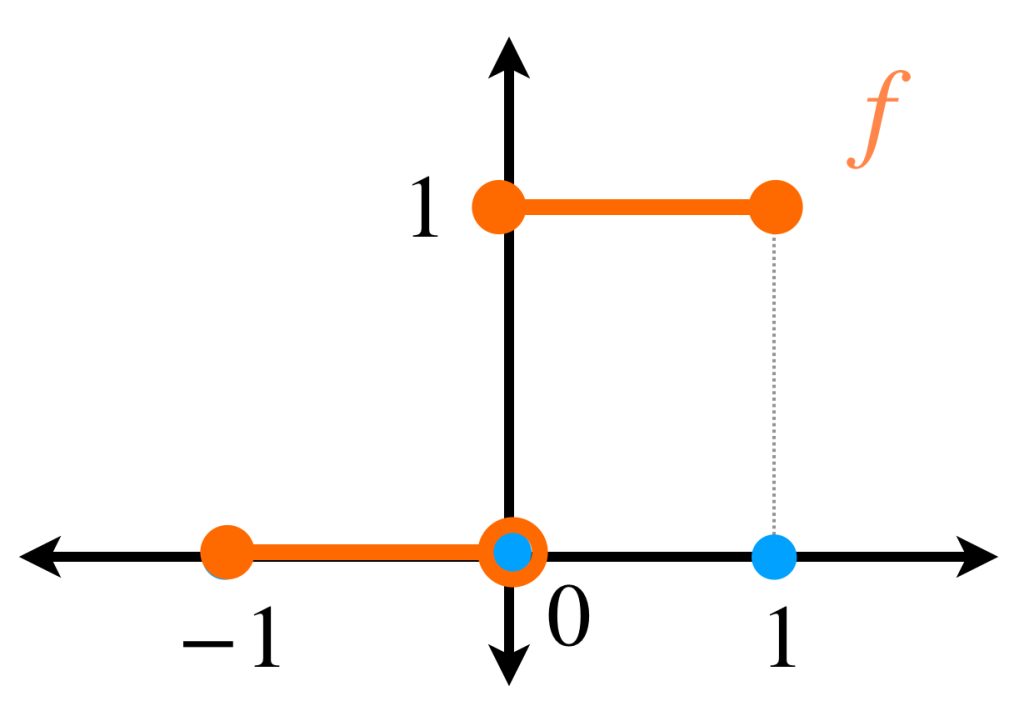
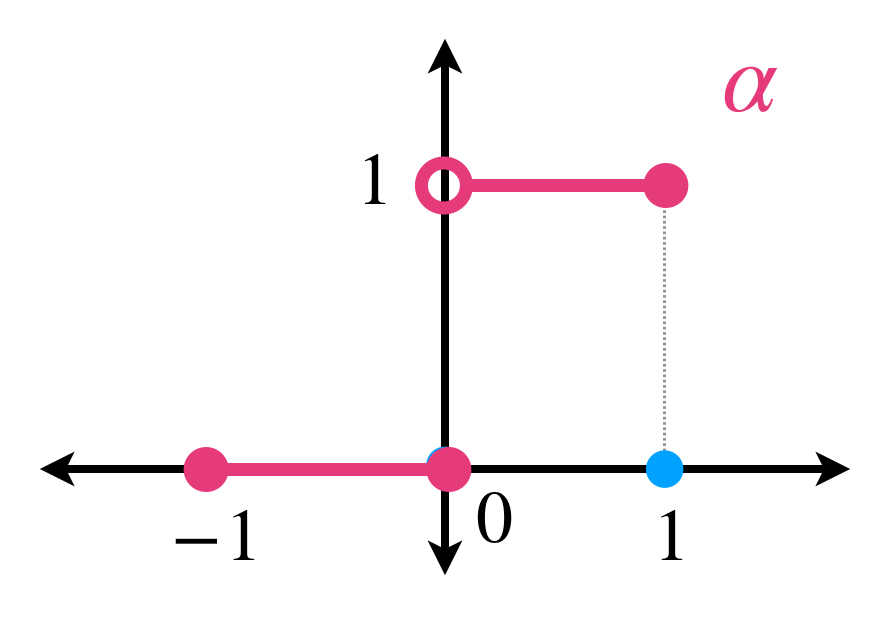
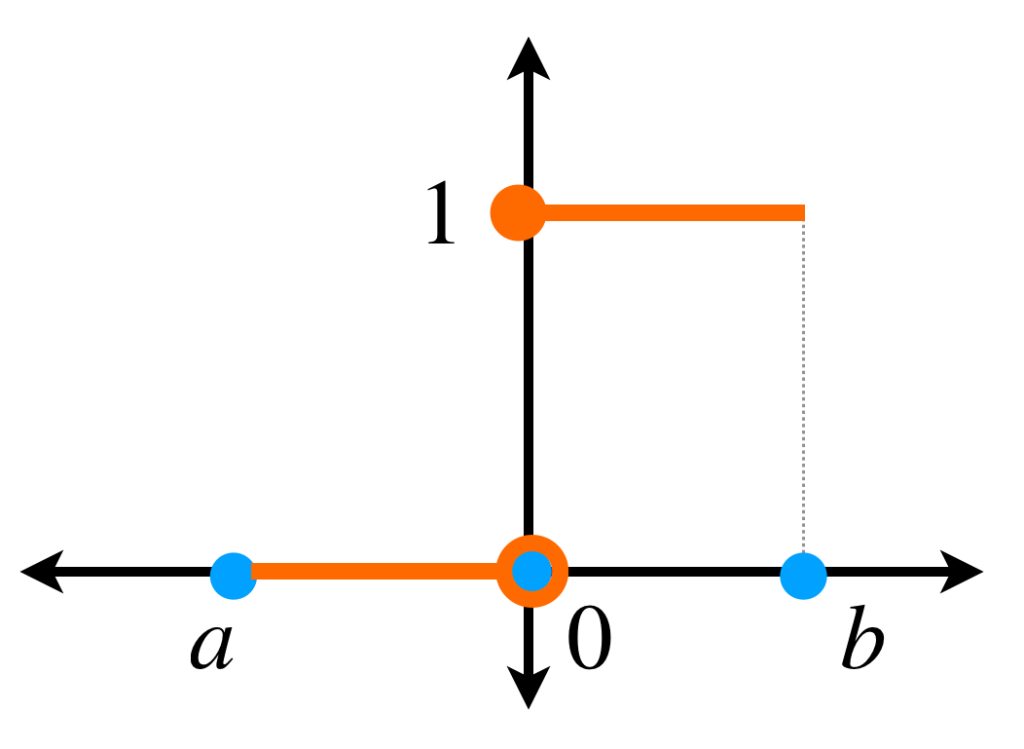
Sean $f:[a,b] \to \mathbb{R}\,$ y $\, \alpha:[a,b] \to \mathbb{R}$ definidas como
\begin{equation*}
f(x) = \begin{cases}
0 &\text{ si } &-1 \leq x <0 \\
1 &\text{ si } &0 \leq x \leq 1.
\end{cases}
\end{equation*}
\begin{equation*}
\alpha (x) = \begin{cases}
0 &\text{ si } &-1 \leq x \leq 0 \\
1 &\text{ si } &0 < x \leq 1 .
\end{cases}
\end{equation*}
Observa que $f$ y $\alpha$ tienen un punto de discontinuidad común que provoca que $\int_{-1}^{1}f \, d\alpha$ no exista. En efecto, si $P= \{x_0=-1,…,x_n =1\}$ es una partición entonces para algún $j \in \{1,…,n\}$
$$x_{j-1} \leq 0 \leq x_j$$
Queda como ejercicio probar que $S(P,f,\alpha)= f(\xi_j)$ con $\xi_j \in [x_{j-1}, x_j],$ y así
$$S(P,f,\alpha)= 0\, \text{ o }\, S(P,f,\alpha)= 1$$
sin importar qué tan pequeños sean los intervalos de la partición, por lo que no existe $\underset{|P| \to 0}{lim} \, S(P,f,\alpha).$
Pese a lo anterior, es sencillo verificar que
$$ \underset{P \in \mathcal{P}_{[a,b]}}{\text{sup} \, \underline{S}_P} = \underset{P \in \mathcal{P}_{[a,b]}}{\text{ínf} \, \overline{S}_P} = 1.$$
La siguiente proposición muestra hipótesis en las que la integral de Riemann-Stieltjes y los límites de las sumas sí coinciden.
Proposición: Sea $f:[a,b] \to \mathbb{R}$ acotada y $\alpha:[a,b] \to \mathbb{R}$ monótona creciente. Si $\int_{a}^{b}f \, d\alpha$ existe, entonces
$$\underset{|P| \to 0}{lim} \, \underline{S}_P \, \text{ y } \, \underset{|P| \to 0}{lim} \, \overline{S}_P$$
existen y
$$\underset{|P| \to 0}{lim} \, \underline{S}_P \, = \, \underset{|P| \to 0}{lim} \, \overline{S}_P = \underset{P \in \mathcal{P}_{[a,b]}}{\text{sup} \, \underline{S}_P} = \underset{P \in \mathcal{P}_{[a,b]}}{\text{ínf} \, \overline{S}_P} = \int_{a}^{b}f \, d\alpha.$$
Demostración:
En el caso no trivial, supongamos que $\alpha$ no es constante en $[a,b].$
Sea $I = \int_{a}^{b}f \, d\alpha.$ Entonces dada $\varepsilon >0$ existe $\delta>0$ tal que si $|P|< \delta$ entonces $|I \, – \, S(P,f,\alpha)|< \varepsilon.$
Supongamos que $P= \{x_0 = a,…, x_n =b\}$ con $|P|< \delta.$ Tomemos $\xi_i, \, \eta_i \in [x_{i-1},x_i], \, i=1,…,n, \,$ tales que
\begin{align}
0 \leq M_i \, – \, f(\xi_i) &< \frac{\varepsilon}{\alpha(b) \, – \, \alpha(a)} \, \, \text{ y } \\
0 \leq f(\eta_i) \, – \, m_i &< \frac{\varepsilon}{\alpha(b) \, – \, \alpha(a)}
\end{align}
Sean
\begin{align}
S’_P&= \sum_{i=1}^{n}f(\xi_i) \, (\alpha(x_i) \, – \, \alpha(x_{i-1})) \, \, \text{ y } \\
S^{\prime \prime}_P&= \sum_{i=1}^{n}f(\eta_i) \, (\alpha(x_i) \, – \, \alpha(x_{i-1}))
\end{align}
entonces
\begin{align}
|I \, – \, S’_P|&< \varepsilon \, \, \text{ y}\\
|I \, – \, S^{\prime \prime}_P|&< \varepsilon.
\end{align}
Por otro lado, por (2),
\begin{align}
\nonumber 0 \leq \overline{S}_P \, – \, S’_P &= \sum_{i=1}^{n}M_i \, (\alpha(x_i) \, – \, \alpha(x_{i-1})) \, – \sum_{i=1}^{n}f(\xi_i) \, (\alpha(x_i) \, – \, \alpha(x_{i-1}))\\
\nonumber &= \sum_{i=1}^{n}[M_i \, – \, f(\xi_i)] \, (\alpha(x_i) \, – \, \alpha(x_{i-1})) \\
\nonumber &< \sum_{i=1}^{n}\frac{\varepsilon}{\alpha(b) \, – \, \alpha(a)}\, (\alpha(x_i) \, – \, \alpha(x_{i-1})) \\
\nonumber &= \frac{\varepsilon}{\alpha(b) \, – \, \alpha(a)}\, \sum_{i=1}^{n} (\alpha(x_i) \, – \, \alpha(x_{i-1})) \\
\nonumber &= \frac{\varepsilon}{\alpha(b) \, – \, \alpha(a)}\, (\alpha(b) \, – \, \alpha(a)) \\
&= \varepsilon.
\end{align}
Análogamente
\begin{align}
0 \leq S^{\prime \prime}_P \, – \, \underline{S}_P < \varepsilon.
\end{align}
De (6), (8) y la desigualdad del triángulo se sigue
$$|\overline{S}_P \, – \, I|\leq |\overline{S}_P\, – \, S’_P|+|S’_P \, – \, I|< \varepsilon + \varepsilon = 2 \varepsilon,$$
mientras que de (7), (9) y la desigualdad del triángulo tenemos
$$|\underline{S}_P \, – \, I|\leq |\underline{S}_P\, – \, S^{\prime \prime}_P|+|S^{\prime \prime}_P \, – \, I|< \varepsilon + \varepsilon = 2 \varepsilon,$$
por lo tanto
$$\underset{|P|\to 0}{lim}\, \overline{S}_P = I = \underset{|P|\to 0}{lim}\, \underline{S}_P .$$
Dado que
$$\underline{S}_P \leq \underset{P \in \mathcal{P}_{[a,b]}}{\text{sup} \, \underline{S}_P} \leq \underset{P \in \mathcal{P}_{[a,b]}}{\text{ínf} \, \overline{S}_P} \leq \overline{S}_P$$
entonces también
$$\underset{|P|\to 0}{lim}\, \underline{S}_P =\underset{P \in \mathcal{P}_{[a,b]}}{\text{sup} \, \underline{S}_P} = \underset{P \in \mathcal{P}_{[a,b]}}{\text{ínf} \, \overline{S}_P} = \underset{|P|\to 0}{lim}\, \overline{S}_P$$
terminando así la prueba.
Para finalizar, veamos la siguiente:
Proposición: Sean $f:[a,b] \to \mathbb{R}$ acotada y $\alpha:[a,b] \to \mathbb{R}$ monótona creciente y continua, entonces
a)
$$\underset{|P| \to 0}{lim} \, \underline{S}_P \, \text{ y } \, \underset{|P| \to 0}{lim} \, \overline{S}_P$$
existen y se cumplen las siguientes igualdades:
\begin{align}
\underset{|P| \to 0}{lim} \, \underline{S}_P &= \underset{P \in \mathcal{P}_{[a,b]}}{\text{sup} \, \underline{S}_P} \\
\underset{|P| \to 0}{lim} \, \overline{S}_P &= \underset{P \in \mathcal{P}_{[a,b]}}{\text{ínf} \, \overline{S}_P}.
\end{align}
b) Si además $\underset{P \in \mathcal{P}_{[a,b]}}{\text{sup}} \, \underline{S}_P = \underset{P \in \mathcal{P}_{[a,b]}}{\text{ínf}} \, \overline{S}_P$ entonces
$$\int_{a}^{b}f \, d\alpha$$
existe y
$$\underset{P \in \mathcal{P}_{[a,b]}}{\text{sup}} \, \underline{S}_P = \int_{a}^{b}f \, d\alpha= \underset{P \in \mathcal{P}_{[a,b]}}{\text{ínf}} \, \overline{S}_P.$$
Demostración:
a) Será suficiente probar (10) y (11). Presentamos la demostración de (11). La igualdad faltante es análoga y se dejará como ejercicio al lector.
Para simplificar la notación, hagamos
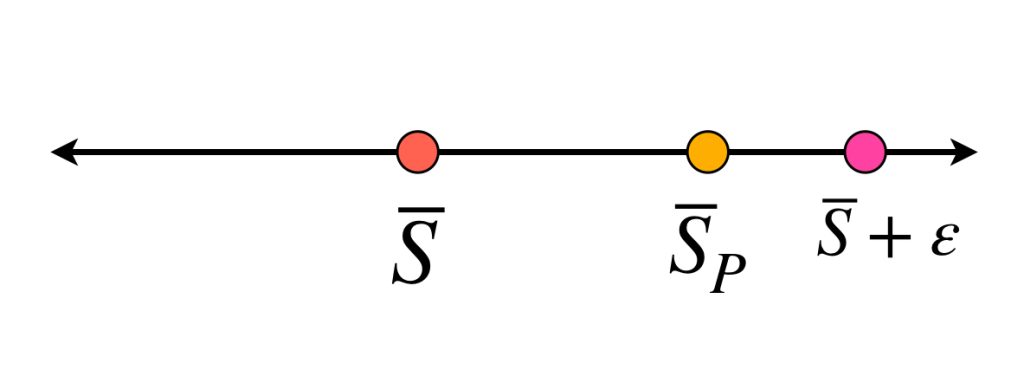
$$\underset{P \in \mathcal{P}_{[a,b]}}{\text{ínf}} \, \overline{S}_P := \overline{S}.$$
Nota que (11) se cumple si y solo si dado $\varepsilon>0$ existe $\delta>0$ tal que si $|P|< \delta$ entonces
\begin{align}
\nonumber &&|\overline{S}_P \, – \, \overline{S}| &< \varepsilon\\
\nonumber &\iff& \overline{S}_P \, – \, \overline{S} &< \varepsilon\\
&\iff& \overline{S}_P &< \overline{S} + \varepsilon
\end{align}
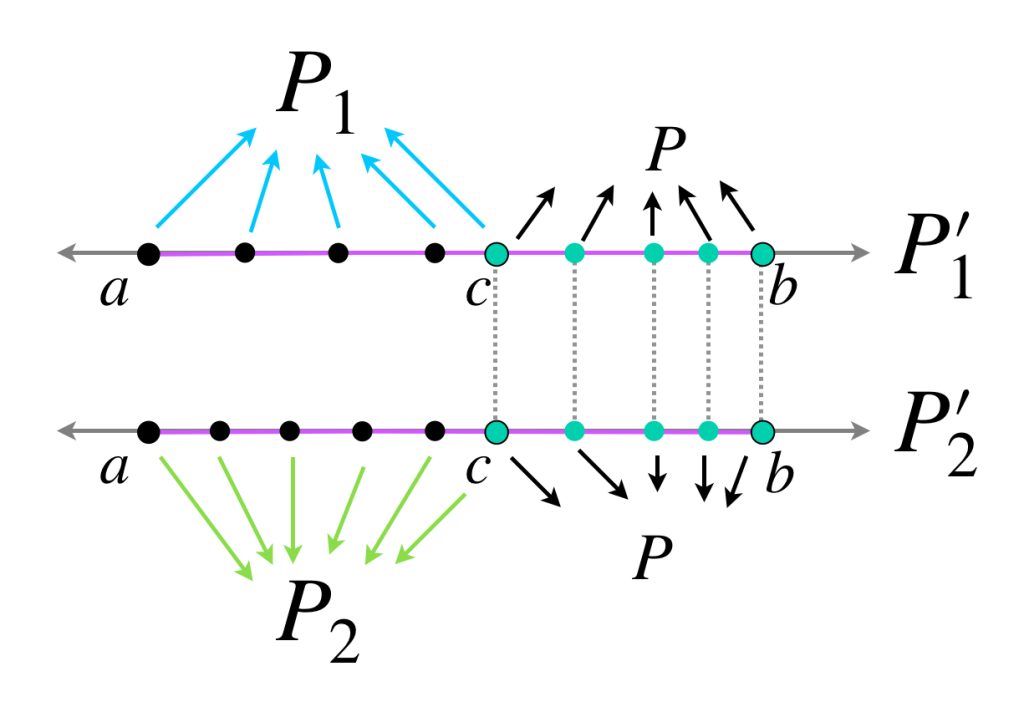
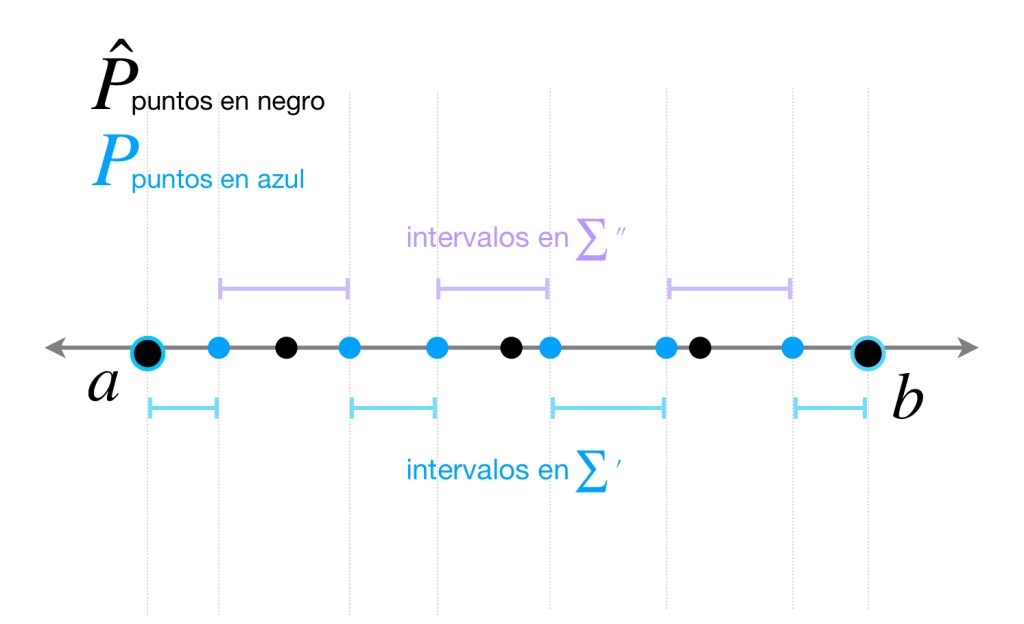
Tomemos $\hat{P}=\{\hat{x_0}=a,…,\hat{x_n}=b\}$ una partición de $[a,b]$ tal que
$$\overline{S}_{\hat{P}}<\overline{S}+ \frac{\varepsilon}{2}.$$
y sea
\begin{align}
\textcolor{RoyalBlue}{M= \underset{x \, \in \, [a,b]}{sup} \, |f(x)|.}
\end{align}
Ya que $\alpha$ es uniformemente continua en $[a,b],$ existe $\eta>0$ tal que si $|x \, – \, x’|< \eta$ entonces
\begin{align}
\textcolor{magenta}{|\alpha(x) \, – \, \alpha(x’)| < \frac{\varepsilon}{4(n+1)M}}.
\end{align}
Ahora tomemos $P=\{x_0=a,…,x_m=b\}$ partición de $[a,b]$ tal que $|P|< \eta$ y
$$|P|< \underset{i \in \{1,…,n\}}{\text{mín}}\, (\hat{x_i}\, – \, \hat{x}_{i-1}).$$
Vamos a mostrar que $\overline{S}_P$ cumple (12).
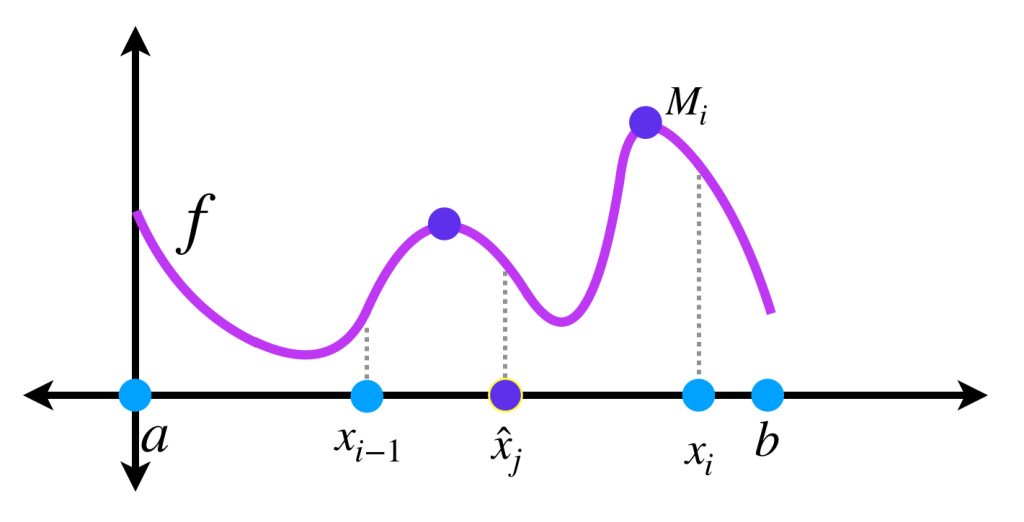
Nota que
\begin{align}
\overline{S}_P &= \sum_{i=1}^{m}M_i \, (\alpha(x_i) \, – \, \alpha(x_{i-1}))\\
&= \sum’ + {\sum}^{\prime \prime}
\end{align}
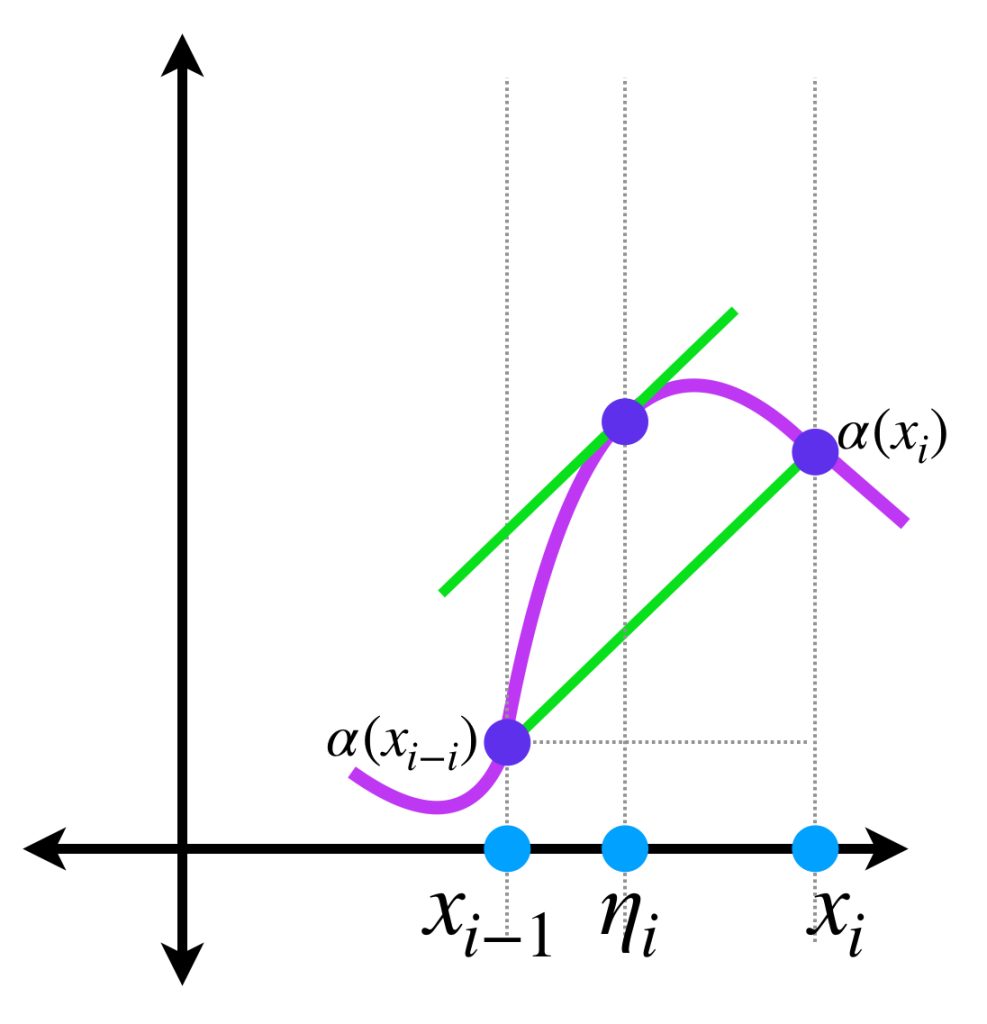
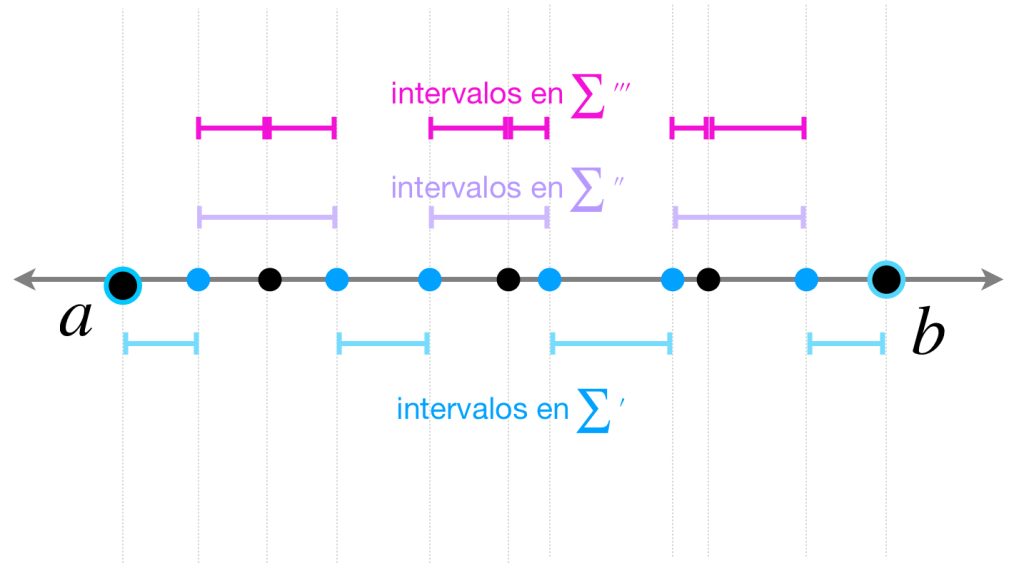
donde $\sum’$ representa a los sumandos cuyos intervalos no tienen puntos de $\hat{P}\,$ y $\, \sum^{\prime \prime}$ representa a los que sí. Observa que, por como fueron elegidas $P$ y $\hat{P},$ cada intervalo generado por $P$ tiene a lo más un punto de $\hat{P},$ así
\begin{align}
\overline{S}_{P \cup \hat{P}} = \sum’ + {\sum}^{\prime \prime \prime}
\end{align}
donde $\sum^{\prime \prime \prime}$ resulta de reemplazar cada sumando en $\sum^{\prime \prime}$ que es de la forma
$$M_i \, (\alpha(x_i) \, – \, \alpha(x_{i-1}))$$
por la expresión
$$\underset{x \, \in \, [x_{i-1},\hat{x}_j]}{\text{sup}}f(x) \, (\alpha(\hat{x}_j) \, – \, \alpha(x_{i-1})) + \underset{x \, \in \, [\hat{x}_j, x_{i},]}{\text{sup}}f(x) \, (\alpha(x_i) \, – \, \alpha(\hat{x}_j) ) $$
donde $\hat{x}_j$ es el punto de $\hat{P}$ en $(x_{i-1}, x_i).$
Por lo tanto de (16) y (17) tenemos
$$\overline{S}_P \, – \, \overline{S}_{P \cup \hat{P}} = {\sum}^{\prime \prime} \, – \, {\sum}^{\prime \prime \prime}.$$
Observa que se satisface al menos una de las siguientes igualdades:
\begin{align}
M_i &= \underset{x \, \in \, [x_{i-1},\hat{x}_j]}{\text{sup}}f(x) \, \text{ o bien} \\
M_i &= \underset{x \, \in \, [\hat{x}_j, x_{i},]}{\text{sup}}f(x)
\end{align}
Si se cumple (18) entonces
\begin{align}
\nonumber M_i \, (\alpha(x_i) \, – \, \alpha(x_{i-1})) \, – \, [\underset{x \, \in \, [x_{i-1},\hat{x}_j]}{\text{sup}}f(x) \, (\alpha(\hat{x}_j) \, – \, \alpha(x_{i-1})) + \underset{x \, \in \, [\hat{x}_j, x_{i},]}{\text{sup}}f(x) \, (\alpha(x_i) \, – \, \alpha(\hat{x}_j) )] = \\
=\textcolor{RoyalBlue}{\left( M_i \, – \, \underset{x \, \in \, [\hat{x}_j, x_{i},]}{\text{sup}}f(x) \right)} \, \textcolor{magenta}{(\alpha(x_i) \, – \, \alpha(\hat{x}_j) )}
\end{align}
Pero si se cumple (19) se sigue que
\begin{align}
\nonumber M_i \, (\alpha(x_i) \, – \, \alpha(x_{i-1})) \, – \, [\underset{x \, \in \, [x_{i-1},\hat{x}_j]}{\text{sup}}f(x) \, (\alpha(\hat{x}_j) \, – \, \alpha(x_{i-1})) + \underset{x \, \in \, [\hat{x}_j, x_{i},]}{\text{sup}}f(x) \, (\alpha(x_i) \, – \, \alpha(\hat{x}_j) )] = \\
=\textcolor{RoyalBlue}{\left(M_i \, – \, \underset{x \, \in \, [x_{i-1},\hat{x}_j]}{\text{sup}}f(x) \right)} \, \textcolor{magenta}{(\alpha(\hat{x}_j) \, – \, \alpha(x_{i-1}) )}
\end{align}
En cualquier caso, de (13) y (14) la diferencia es a lo más
$$\frac{\textcolor{RoyalBlue}{2M}\textcolor{magenta}{\varepsilon}}{\textcolor{magenta}{4(n+1)M}} = \frac{\varepsilon}{2(n+1)}$$
Entonces.
$$\overline{S}_P \, – \, \overline{S}_{P \cup \hat{P}} \leq \frac{\varepsilon(n+1)}{2(n+1)} = \frac{\varepsilon}{2}.$$
Más aún
$$\overline{S}_{P \cup \hat{P}} \leq \overline{S}_\hat{P} < \overline{S}+\frac{\varepsilon}{2}$$
con lo cual queda demostrada la proposición.
b) Dado que para cualquier $P \in \mathcal{P}_{[a,b]}$
$$\underline{S}_P \leq S(P,f,\alpha) \leq \overline{S}_P$$
entonces haciendo $|P| \to 0$ concluimos:
$$\underset{P \in \mathcal{P}_{[a,b]}}{\text{sup} \, \underline{S}_P} = \int_{a}^{b}f \, d\alpha = \underset{P \in \mathcal{P}_{[a,b]}}{\text{ínf} \, \overline{S}_P}.$$
Más adelante…
¡Gracias por acompañarnos en la exposición de este curso! Si deseas continuar, puedes consultar el contenido correspondiente a Análisis Matemático II. La comunidad sigue creciendo y ya trabaja creando notas con ejercicios que motiven el aprendizaje. Pronto te las compartiremos.
Tarea moral
- En el ejemplo descrito al inicio, demuestra que
a)
$$S(P,f,\alpha)= f(\xi_j)$$
con $\xi_j \in [x_{j-1}, x_j]$ donde $[x_{j-1}, x_j]$ es el intervalo de la partición que tiene al cero.
Prueba también que para todo $\delta>0$ existe una partición $P$ con $|P|< \delta$ tal que
$S(P,f,\alpha)= 0$ o $S(P,f,\alpha)= 1$
dependiendo el punto $\xi_j$ elegido. Concluye que no existe $\underset{|P| \to 0}{lim} \, S(P,f,\alpha).$
b) Verifica que
$$ \underset{P \in \mathcal{P}_{[a,b]}}{\text{sup} \, \underline{S}_P} = \underset{P \in \mathcal{P}_{[a,b]}}{\text{ínf} \, \overline{S}_P} = 1.$$
- Demuestra la igualdad (10).
Enlaces