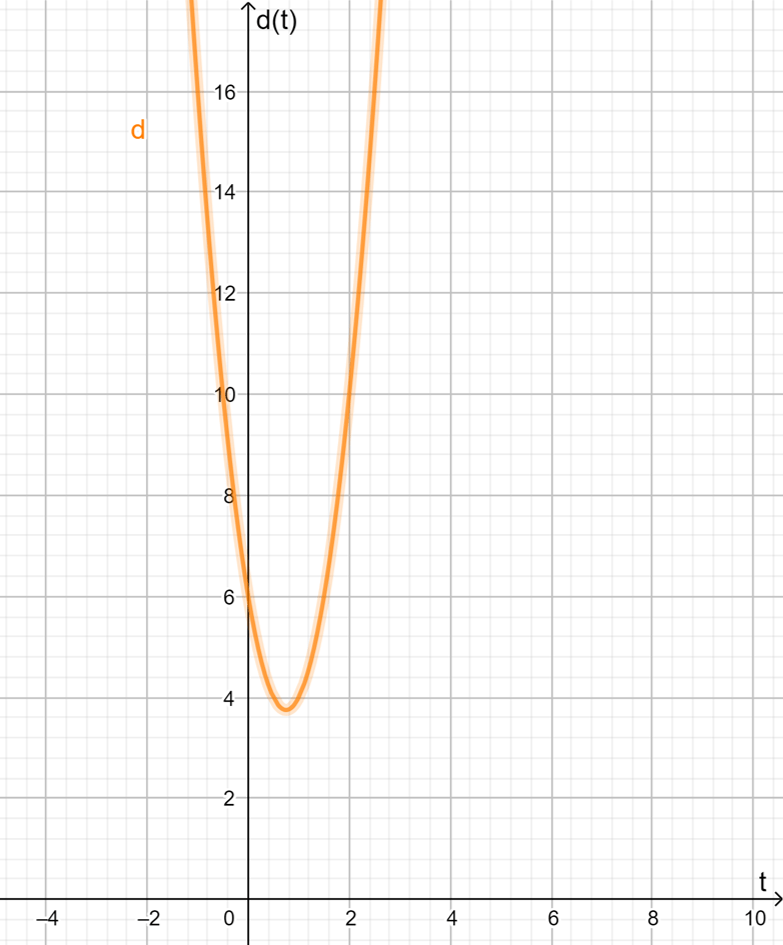Archivo del Autor: Karen González Cárdenas

Cálculo Diferencial e Integral I: Velocidad y aceleración

Por Karen González Cárdenas

Introducción

Para los problemas que veremos en esta entrada, será necesario recordar algunos conceptos de la Física relacionados con el Movimiento rectilíneo uniforme que posiblemente estudiaste en el bachillerato.

Recordemos que la velocidad se encuentra expresada por:
$v = \frac{d}{t} .$
Esta igualdad modela el movimiento de un punto sobre una recta en una distancia $d$ en un tiempo $t$ con una velocidad uniforme $v$ .

De la ecuación anterior podemos obtener que la distancia es:
$\begin{matrix} (1) & d = v \cdot t . \end{matrix}$

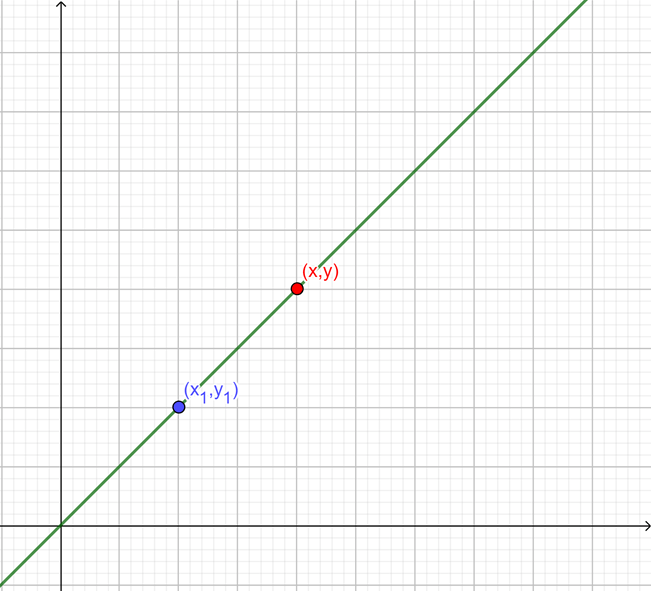
Ahora si consideramos a un par de puntos $(d_{1}, t_{1})$ y $(d_{2}, t_{2})$ tales que:
$\begin{aligned} d_{1} & = v t_{1} & d_{2} & = v t_{2} \end{aligned}$

Así al sustituir en $(1)$ tendríamos que:
$d_{2} - d_{1} = v (t_{2} - t_{1}) \Rightarrow v = \frac{d_{2} - d_{1}}{t_{2} - t_{1}}$

que es justo la velocidad media.

Supongamos ahora que el movimiento ya no es de velocidad uniforme y que la función de distancia recorrida del punto $p$ en un tiempo $t$ está dada como:
$d = d (t) .$

Por lo que ahora la función de velocidad media de $p$ en un intervalo $[t_{1}, t_{2}]$ se define como:
$\frac{d_{2} - d_{1}}{t_{2} - t_{1}} = \frac{d (t_{2}) - d (t_{1})}{t_{2} - t_{1}} .$

Tomemos a $t_{2} - t_{1} = h$ por lo que tenemos las siguientes conclusiones:

$t_{2} = t_{1} + h$ donde $h \neq 0$
$d (t_{2}) = d (t_{1} + h)$
$[t_{1} . t_{2}] = [t_{1}, t_{1} + h]$

En consecuencia la velocidad media queda:
$\frac{d (t_{1} + h) - d (t_{1})}{h} .$
Aplicamos límite a la expresión anterior para obtener la velocidad instantánea (rapidez o sólo velocidad):
$lim_{h \to 0} \frac{d (t_{1} + h) - d (t_{1})}{h} .$
Generalizando al considerar cualquier tiempo $t$ observamos que:
$lim_{h \to 0} \frac{d (t + h) - d (t)}{h} = d^{'} (t) .$

Concluyendo con la siguiente igualdad para la función velocidad de un punto $p$ :
$v (t) = d^{'} (t) .$

Y a la aceleración media como:
$a (t) = v^{'} (t) = d^{''} (t) .$

Problema 1

Supongamos que tenemos una partícula cuyo movimiento se encuentra modelado por la función:
$d (t) = 4 t^{2} - 6 t + 6$
con la distancia expresada en metros y el tiempo en segundos.

Se nos pide encontrar:

Su distancia recorrida cuando $t = 0$ .
Su velocidad al iniciar su movimiento.
La velocidad alcanzada transcurridos 3 segundos.
La velocidad final a los 5 segundos.
Su aceleración.

Solución:

Veamos que la podemos obtener evaluando la función de movimiento cuando $t = 0$ :
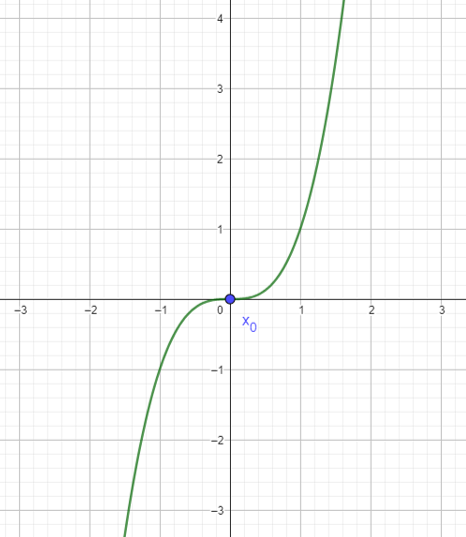
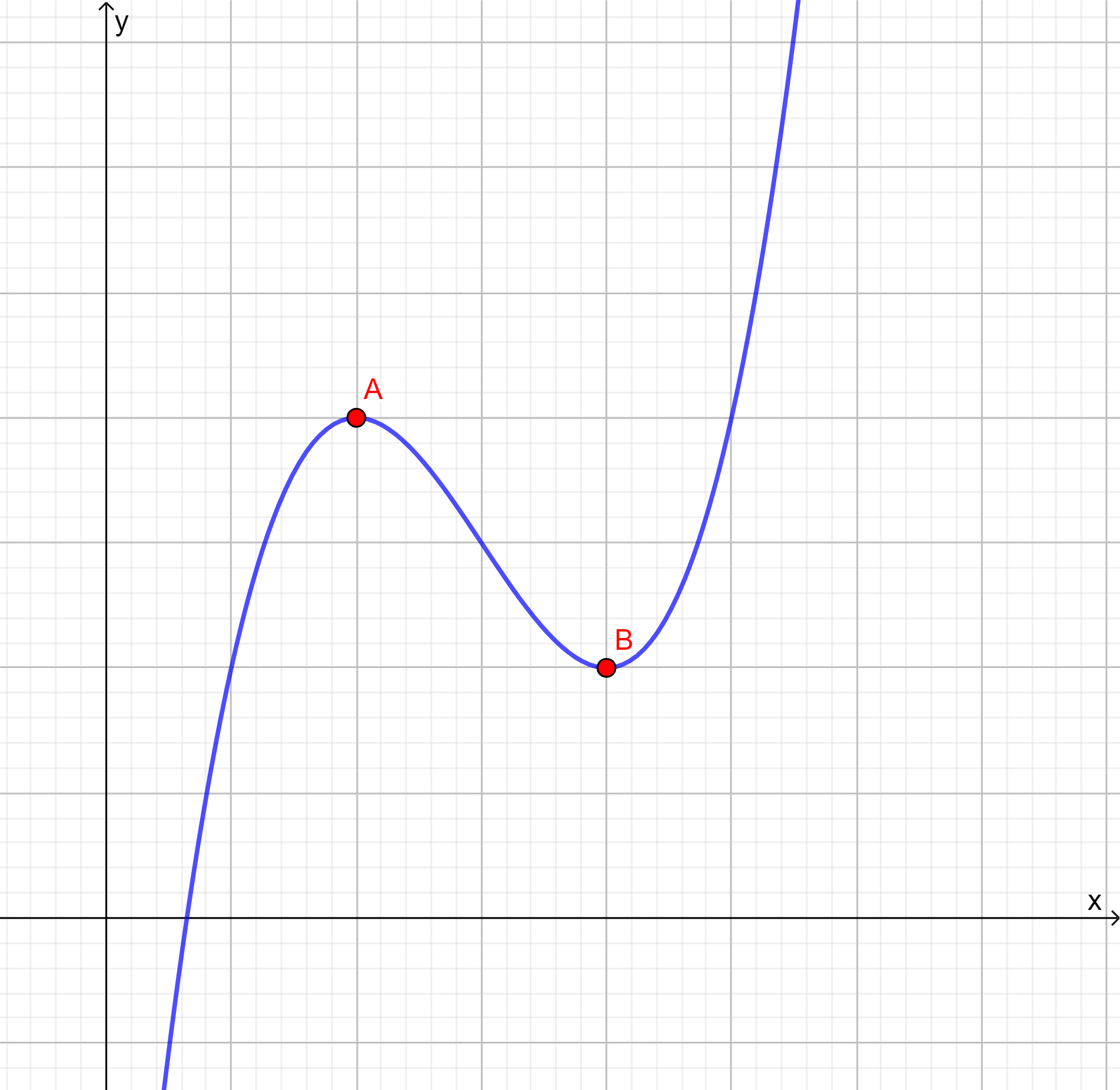
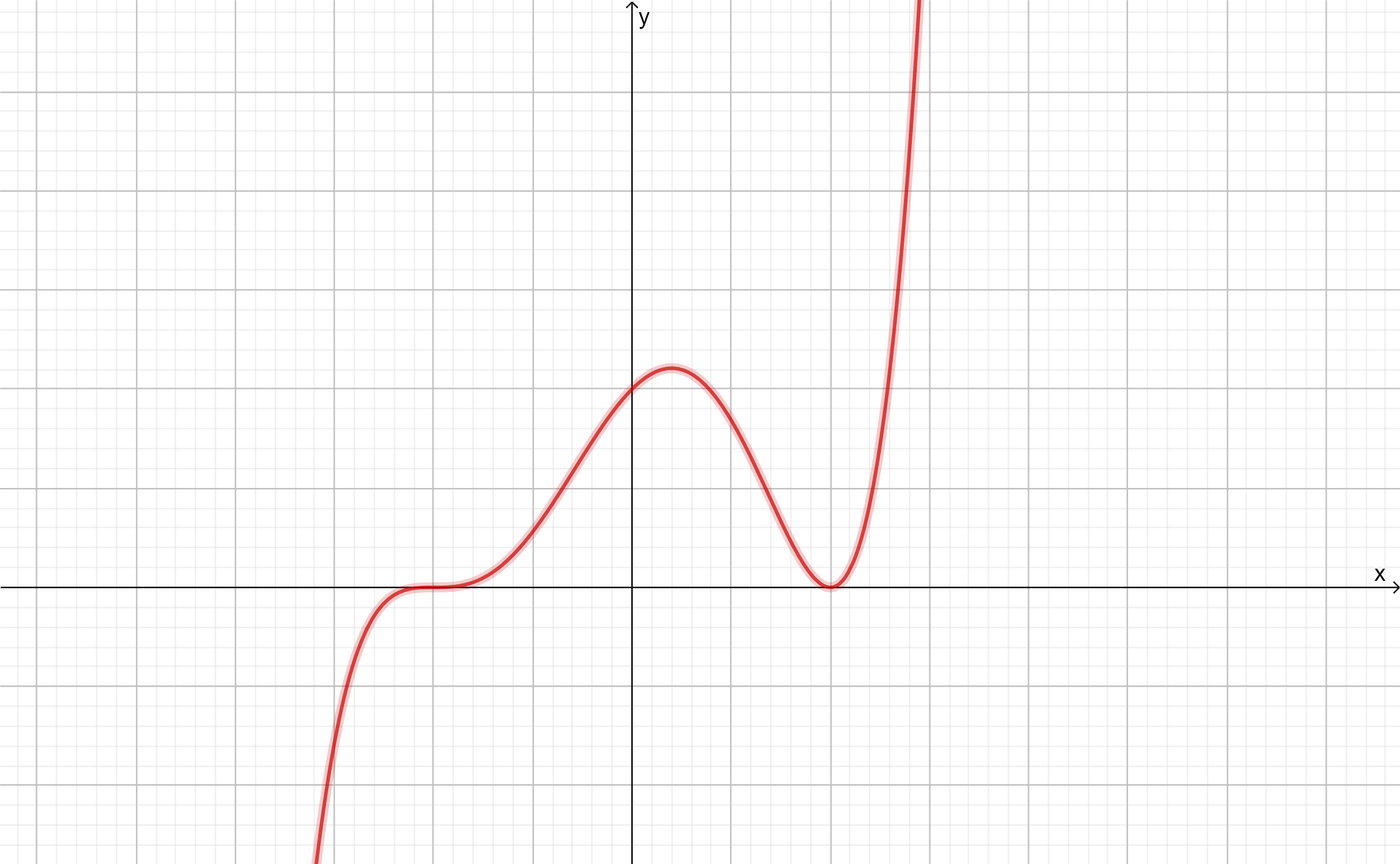
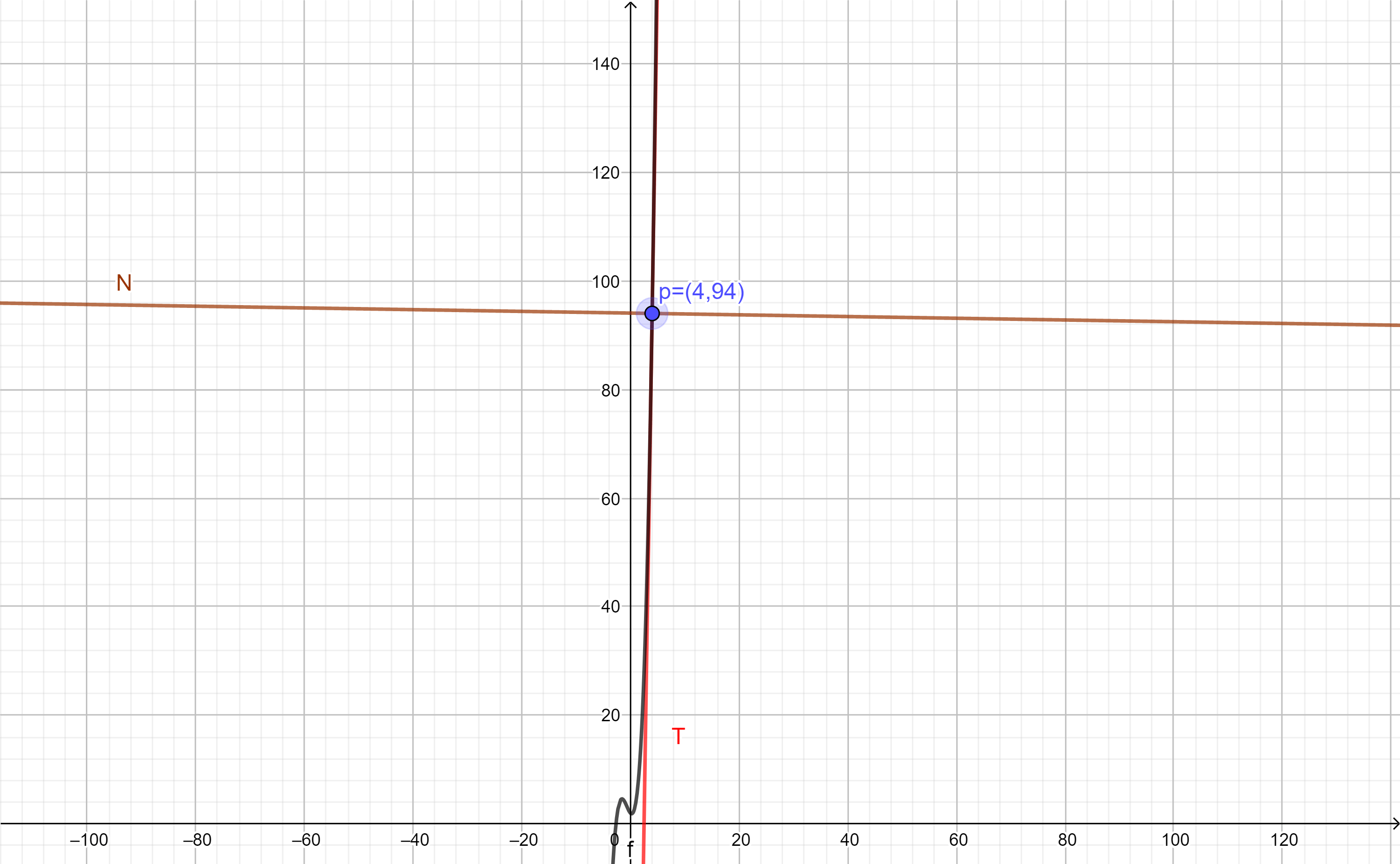
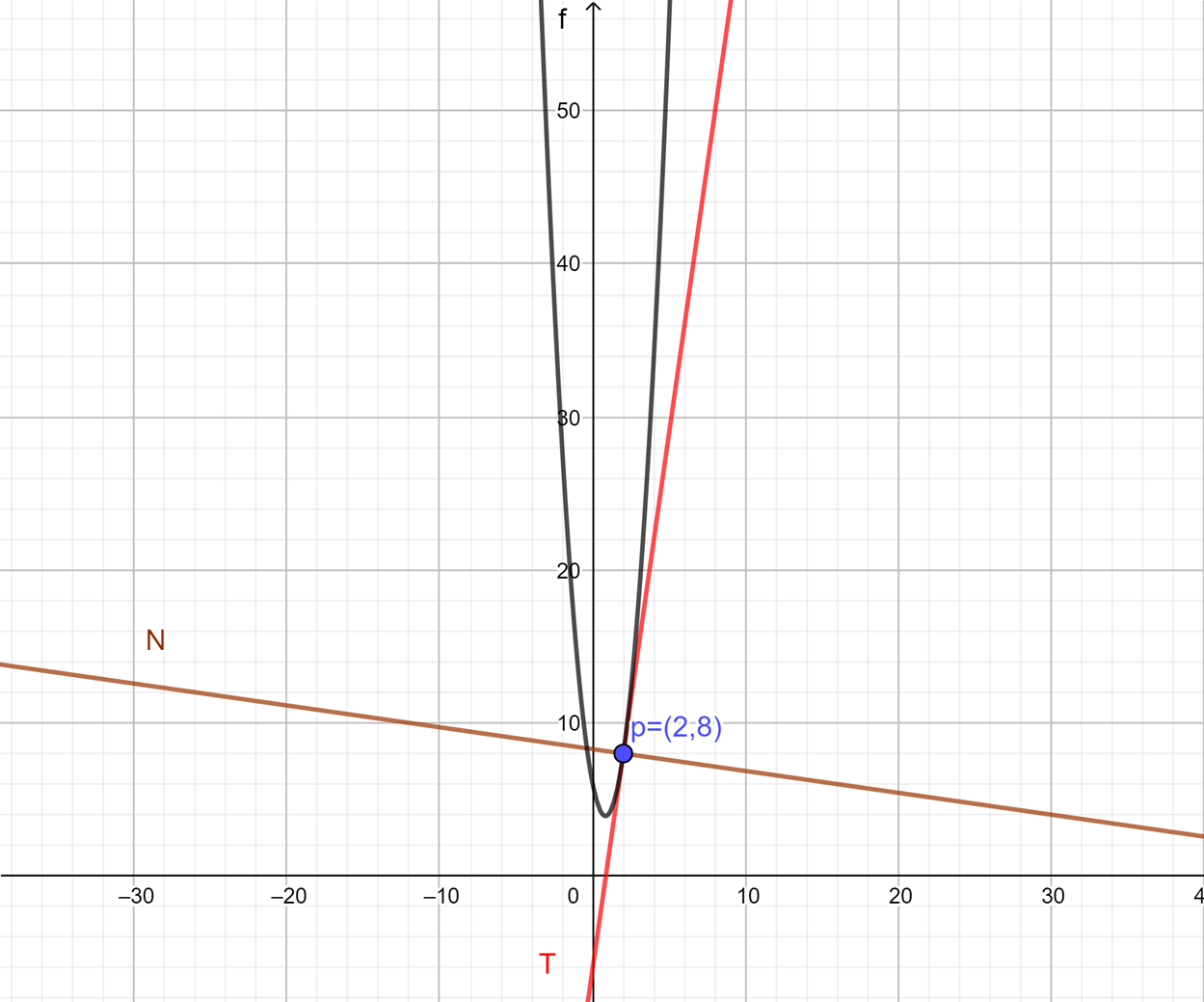
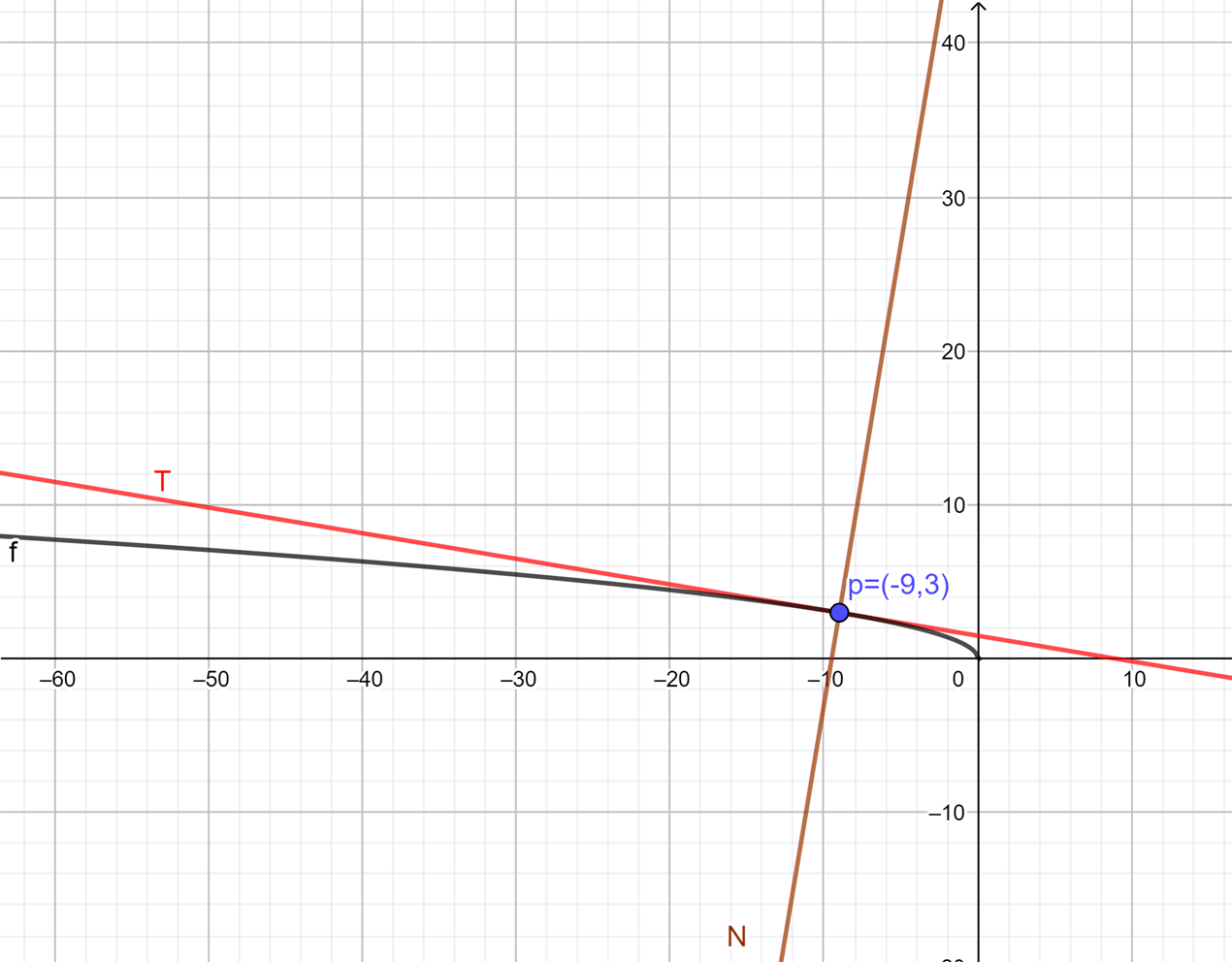
$d (0) = 4 (0)^{2} - 6 (0) + 6 = 6 m .$
Para la velocidad al iniciar basta derivar $d$ y evaluarla con $t = 0$ :
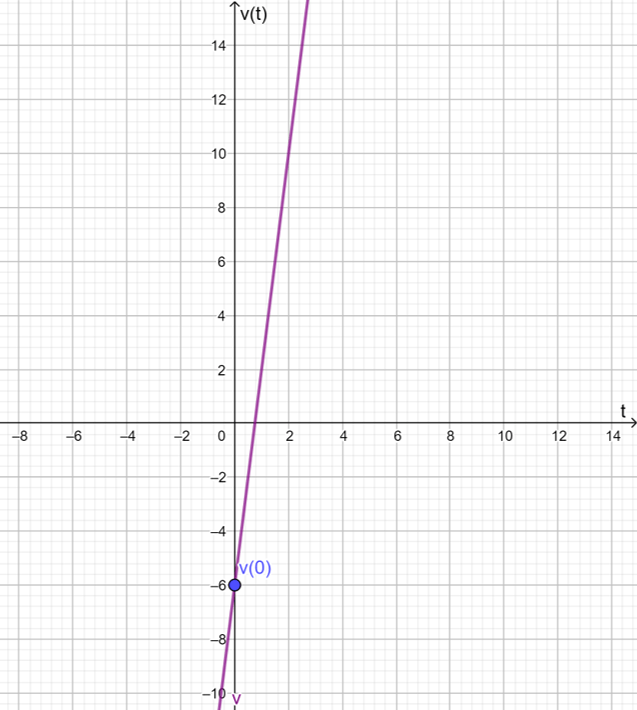
$v (t) = d^{'} (t) = 8 t - 6.$
De este modo:
$v (0) = - 6 \frac{m}{s} .$
Esto lo podemos ver en la gráfica de la función $v$ :

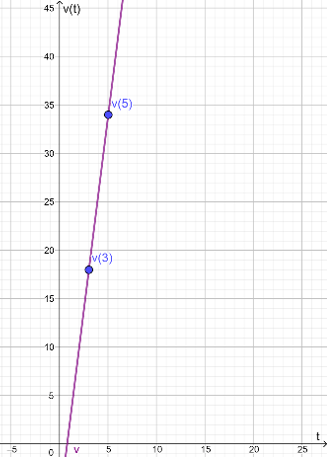
Evaluemos la función $v$ con $t = 3$ :
$\begin{aligned} v (3) & = 8 (3) - 6 \\ = 24 - 6 \\ ∴ v (3) & = 18 \frac{m}{s} . \end{aligned}$
Ahora cuando $t = 5$ :
$\begin{aligned} v (5) & = 8 (5) - 6 \\ = 40 - 6 \\ ∴ v (5) & = 34 \frac{m}{s} . \end{aligned}$

Observamos con lo anterior que la velocidad es creciente.

Debemos obtener la segunda derivada de la función $d$ , que es equivalente a derivar la velocidad:
$\begin{aligned} a (t) & = v^{''} (t) \\ = 8 \frac{m}{s^{2}} . \end{aligned}$
Por lo que tenemos que su aceleración es constante.

Problema 2

Un proyectil es lanzado, tenemos que la función que describe la altura alcanzada al tiempo $t$ es:
$d (t) = - 3 t^{2} + 54 t$

¿En qué instante alcanza su altura máxima y cuál es su valor?
Solución:

Comenzaremos derivando la función $d$ :
$d^{'} (t) = - 6 t + 54.$

Igualamos a cero para encontrar el máximo:
$\begin{aligned} d^{'} (t) = 0 & \Leftrightarrow - 6 t + 54 = 0 \\ \Leftrightarrow - t + 9 = 0 \\ \Leftrightarrow t = 9 \end{aligned}$

Aplicando el Criterio de la segunda derivada comprobamos que se trata de un máximo cuando $t = 9$ :
$d^{''} (t) = - 6 < 0.$

Así para obtener el valor de la altura basta sustituir $t = 9$ en la función $d$ :
$\begin{aligned} d (9) & = - 3 (9)^{2} + 54 (9) \\ = - 3 (81) + 486 \\ = - 243 + 486 \\ = 243 \end{aligned}$
$∴$ La altura es de $243 m$ .

Problema 3

Tenemos que la distancia recorrida por una partícula se expresa mediante la función:
$d (t) = 2 t^{3} - 5 t^{2} + 10 t$
donde consideramos a $d$ en metros y a $t$ en segundos.
¿Cuál es su velocidad cuando:

$t = 1$ ,
$t = \frac{3}{2}$ ,
$t = 0$ ?

Solución:
Primero obtenemos la función velocidad derivando $d$ :
$v (t) = d^{'} (t) = 6 t^{2} - 10 t + 10.$
Ahora evaluamos los valores que nos piden:

Con $t = 1$ :
$v (1) = 6 (1)^{2} - 10 (1) + 10 = 6.$
$∴ v (1) = 6 \frac{m}{s} .$
Con $t = \frac{3}{2}$ :
$v (\frac{3}{2}) = 6 {(\frac{3}{2})}^{2} - 10 (\frac{3}{2}) + 10 = \frac{17}{2} .$
$∴ v (\frac{3}{2}) = \frac{17}{2} \frac{m}{s} .$
Con $t = 0$ :
$v (0) = 6 (0)^{2} - 10 (0) + 10 = 10.$
$∴ v (0) = 10 \frac{m}{s} .$

Después de ver estos problemas, te dejamos a continuación una lista de ejercicios para que puedas practicar el tema visto en esta entrada.

Más adelante

En la próxima entrada, veremos que haciendo uso de la derivada podemos obtener la razón de cambio de dos o más variables relacionadas en un problema.

Tarea moral

Una pelota es lanzada desde el suelo hacia arriba y su altura sigue la función:
$d (t) = 30 t - 5 t^{2} .$
Determina cuál es la altura máxima que alcanza la pelota.
La distancia recorrida por un automóvil se encuentra definida por la función:
$m (t) = t^{2} - 3 t + 1$
donde estamos considerando a $m$ expresada en kilómetros y a $t$ en horas.
Se requiere obtener:
- Su distancia recorrida cuando $t = 0.$
- Su velocidad al iniciar su movimiento.
- La velocidad alcanzada transcurridas 2 horas.
- La velocidad final a las 6 horas.
- Su aceleración.

Entradas relacionadas

Ir a: Cálculo Diferencial e Integral I
Entrada anterior del curso: Cálculo Diferencial e Integral I: Problemas de optimización.
Entrada siguiente del curso: Cálculo Diferencial e Integral I: Razón de cambio.
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Problemas de optimización

Por Karen González Cárdenas

2 respuestas

Introducción

Ya que hemos revisado dos criterios importantes para determinar si un punto crítico de una función es un máximo o un mínimo, en esta entrada veremos que la obtención de los mismos tiene variadas aplicaciones prácticas.

En algunos problemas podría resultar fácil determinar la función que deseamos optimizar (maximizar o minimizar) ya que puede ser conocida previamente. Sin embargo, nos podemos enfrentar a casos más complicados donde no resulte inmediato obtenerla y expresarla en términos de una variable. Es por eso que damos las siguientes recomendaciones generales:

Identifica la función de la cual se desea encontrar su máximo o su mínimo.
En caso de que la función resulte ser de dos o más variables, observa los datos dados en el problema que te permitan expresarlas en función de una sola variable.
Si el problema lo necesita, realiza una representación gráfica del planteamiento.

Problema 1

Encuentra dos números cuya suma sea $40$ y su producto sea máximo.
Solución:

Sabemos que:
$\begin{matrix} (2) & x + y = 40. \end{matrix}$
Y lo que nos piden maximizar es el producto:
$P = x y .$
Para obtener la función a maximizar debemos poner a la variable $y$ en términos de $x$ , por ello nos apoyaremos en la primera ecuación:
$\begin{matrix} (3) & y = 40 - x . \end{matrix}$
Sustituyendo lo anterior tenemos que la función a maximizar:
$\begin{aligned} P (x) & = x (40 - x) \\ = 40 x - x^{2} \\ ∴ P (x) & = 40 x - x^{2} . \end{aligned}$

Comencemos por buscar los valores críticos de la función, en consecuencia, derivamos una vez $P (x)$ :
$P^{'} (x) = 40 - 2 x .$
Ahora igualamos a cero la primera derivada:
$\begin{aligned} P^{'} (x) = 0 & \Leftrightarrow 40 - 2 x = 0 \\ \Leftrightarrow 20 - x = 0 \\ \Leftrightarrow x = 20 \end{aligned}$

Para obtener el máximo utilizaremos el Criterio de la primera derivada, así cuando:
Caso 1: $x < 20$
$\begin{aligned} P^{'} (19) & = 40 - 2 (19) \\ (que es positivo) & = 2 \end{aligned}$

Caso 2: $x > 20$
$\begin{aligned} P^{'} (21) & = 40 - 2 (21) \\ (que es negativo) & = - 2 \end{aligned}$
Concluimos que $P$ tiene un máximo cuando $x = 20$ .

Para obtener el valor de $y$ sustituimos en $(2)$ :
$y = 40 - 20 \Rightarrow y = 20.$

Por lo tanto los números buscados son $x = 20$ y $y = 20$ .

Observamos que en el problema anterior no fue necesario realizar algún dibujo que nos facilitara su solución. En los siguientes problemas veremos que una representación gráfica puede ser de gran utilidad.

Problema 2

De los rectángulos con perímetro fijo, ¿Cuál tiene el área máxima?

Solución:
Consideremos a $P$ como el perímetro fijo y a $A$ el área del rectángulo, de lo anterior observamos:
$\begin{aligned} A & = x y & P & = 2 x + 2 y \end{aligned}$

Para obtener la función a maximizar despejamos del perímetro a la variable $y$ :
$\begin{aligned} P = 2 x + 2 y & \Rightarrow P - 2 x = 2 y \\ \Rightarrow \frac{P}{2} - x = y \end{aligned}$

Así la función sería:
$\begin{aligned} f (x) & = x (\frac{P}{2} - x) \\ ∴ f (x) & = \frac{P}{2} x - x^{2} . \end{aligned}$

Ahora buscaremos los puntos críticos de $f$ derivando una vez:
$f^{'} (x) = \frac{P}{2} - 2 x .$
E igualando la derivada a cero:
$\begin{aligned} f^{'} (x) = 0 & \Leftrightarrow \frac{P}{2} - 2 x = 0 \\ \Leftrightarrow \frac{P}{2} = 2 x \\ \Leftrightarrow \frac{P}{4} = x \end{aligned}$

Para determinar que es máximo utilizaremos el Criterio de la segunda derivada, por lo que derivamos una segunda vez a la función:
$f^{''} (x) = - 2 < 0.$
Por lo que $f$ tiene un máximo cuando $x = \frac{P}{4}$ .

Obtenemos el valor de $y$ sustituyendo $x = \frac{P}{4}$ :
$\begin{aligned} y & = \frac{P}{2} - \frac{P}{4} \\ = \frac{P}{4} \end{aligned}$

Concluimos que el rectángulo buscado es aquel que tiene lados $x = \frac{P}{4}$ y $y = \frac{P}{4}$ .

Problema 3

Calcular el radio y la altura de los cilindros de volumen máximo y mínimo que puedan inscribirse en un cono con un radio de $6 c m$ y $12 c m$ de altura. En la siguiente imagen podemos ver más claro el planteamiento anterior:

Solución:
Tenemos que el radio está dado por $B C$ y que la altura por $A B$ :
$\begin{aligned} B C & = 6 & A B & = 12 \end{aligned}$
Además el volumen de un cilindro está dado por la ecuación:
$V = π x^{2} y .$
donde $x$ es el radio y $y$ la altura.

Lo que queremos calcular es:
$\begin{aligned} B E & = x & B D & = y \end{aligned}$

Observemos que de la imagen anterior tenemos

de donde el triángulo formado por los puntos $A, B, C$ es semejante con el triángulo formado por $F, E, C$ :
$△ A B C \sim △ F E C .$

Por lo que tenemos la siguiente igualdad:
$\frac{B C}{E C} = \frac{A B}{F E} .$
Sustituimos $B C = 6$ y $A B = 12$ :
$\frac{6}{E C} = \frac{12}{F E} .$
Además, como tenemos que para $E C$ se cumple la igualdad:
$\begin{aligned} E C & = B C - B E \\ (por B E = x) & = 6 - x \end{aligned}$

Por lo anterior y recordando que $y = F E$ se sigue:
$\frac{6}{6 - x} = \frac{12}{y} .$

Despejando a $y$ de la igualdad anterior:
$\begin{aligned} \frac{6}{6 - x} = \frac{12}{y} & \Leftrightarrow \frac{6 y}{6 - x} = 12 \\ \Leftrightarrow 6 y = 12 (6 - x) \\ \Leftrightarrow y = \frac{72 - 12 x}{6} \\ \Leftrightarrow y = 12 - 2 x \end{aligned}$

Obtenemos la función a maximizar sustituyendo $y = 12 - 2 x$ en $V = π x^{2} y$ :
$\begin{aligned} V (x) & = π x^{2} (12 - 2 x) \\ = 12 π x^{2} - 2 π x^{3} \end{aligned}$

Derivemos $V (x)$ :
$V^{'} (x) = 24 π x - 6 π x^{2} .$

Igualemos a cero para obtener los valores críticos:
$\begin{aligned} V^{'} (x) = 0 & \Leftrightarrow 24 π x - 6 π x^{2} = 0 \\ (dividimos entre 6 π) & \Leftrightarrow 4 x - x^{2} \\ \Leftrightarrow x (4 - x) = 0 \\ \Leftrightarrow x = 0 o x = 4 \end{aligned}$

Determinaremos si se trata de un máximo o un mínimo utilizaremos el Criterio de la segunda derivada considerando:
$V^{''} (x) = 24 π - 12 π x .$

Veamos para $x = 0$ :
$V^{''} (0) = 24 π > 0,$
por lo que en consecuencia $V$ tiene un mínimo.

Ahora para $x = 4$ :
$V^{''} (4) = - 24 π < 0,$
por lo tanto $V$ tiene un máximo.

Para obtener las dimensiones recordemos que:
$y = 12 - 2 x .$

Cilindro con volumen mínimo
$x = 0 y y = 12 - 2 (0) = 12$

Cilindro con volumen máximo
$x = 4 y y = 12 - 2 (4) = 4$

Problema 4

Hallar los puntos sobre la gráfica de la función $f (x) = x^{3}$ cuyas abscisas difieren en $k$ unidades tal que la recta que los une tenga pendiente mínima:

Solución:
La pendiente de la recta que une el par de puntos de la imagen está dada por:
$\begin{aligned} m & = \frac{(x - k)^{3} - x^{3}}{(x - k) - x} . \end{aligned}$

Ahora simplificando lo anterior obtenemos la función a minimizar:
$m (x) = 3 x^{2} - 3 k x + k^{2} .$

Derivamos e igualamos a cero:
$m^{'} (x) = 6 x - 3 k \Rightarrow 6 x - 3 k = 0$
Por lo que veamos si cuando $x = \frac{k}{2}$ se trata de un mínimo usando el Criterio de la segunda derivada:
$m^{''} (x) = 6 > 0.$

Concluimos que $m$ tiene un mínimo cuando $x = \frac{k}{2}$ y hallamos los puntos sustituyendo en $f (x) = x^{3}$ :
$f (\frac{k}{2}) = {(\frac{k}{2})}^{3} = \frac{k^{3}}{8} .$

Por lo que los puntos que cumplen son de la forma:
$(\frac{k}{2}, \frac{k^{3}}{8}) .$

A continuación, te presentamos una lista de ejercicios que te permitirán reforzar lo visto en esta entrada, verás que algunos de ellos tienen planteamientos similares.

Más adelante

Ya que hemos revisado algunos problemas que involucran obtener el máximo o mínimo de una función en distintos planteamientos, en la próxima entrada veremos problemas relacionados con los temas de velocidad y aceleración donde igualmente el uso de la derivada será fundamental para su solución.

Tarea moral

Obtener dos números cuyo producto sea $16$ y cuya suma sea mínima.
Hallar las dimensiones del rectángulo con perímetro de $72$ unidades y de área máxima.
Obtener las coordenadas del punto $A$ sobre la curva $f (x) = x^{2}$ más cercano al punto $B = (3, 0)$ .

Utilizando un cartón de forma cuadrada de 12 cm de lado se desea construir una caja abierta recortando cuadrados iguales de las esquinas y doblando hacia arriba. Por lo que se te pide determinar la longitud del lado $x$ de los cuadrados de las esquinas para que la caja:
- Tenga volumen máximo
- Tenga volumen mínimo

Entradas relacionadas

Ir a: Cálculo Diferencial e Integral I
Entrada anterior del curso: Cálculo Diferencial e Integral I: Localización de máximos y mínimos. Regiones de convexidad y puntos de inflexión.
Entrada siguiente del curso: Cálculo Diferencial e Integral I: Velocidad y aceleración.
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Localización de máximos y mínimos. Regiones de convexidad y puntos de inflexión

Por Karen González Cárdenas

Deja un comentario

Introducción

En la sección anterior vimos cómo encontrar los máximos y mínimos de una función haciendo uso del Criterio de la primera derivada. En esta entrada veremos un criterio más que nos ayudará a localizar los puntos críticos de una función haciendo uso de la segunda derivada. Además, veremos los conceptos de convexidad, concavidad y puntos de inflexión.

Criterio de la segunda derivada

Teorema (Criterio de la segunda derivada): Sea $f : (a, b) \to R$ una función de clase $C^{(2)}$ en un punto $x_{0} \in (a, b)$ y $f^{'} (x_{0}) = 0$ .

Si $f^{''} (x_{0}) > 0 \Rightarrow x_{0}$ es un mínimo local de $f$ .
Si $f^{''} (x_{0}) < 0 \Rightarrow x_{0}$ es un máximo local de $f$ .

Observación: una función $f$ es de clase $C^{(k)}$ si su k-ésima derivada existe y sus $k$ derivadas son continuas.

Demostración 2:
Para este punto queremos demostrar que existe un intervalo $(x_{0} - r, x_{0} + r)$ donde:

$f^{'} (x) > 0$ para toda $x \in (x_{0} - r, x_{0})$ .
$f^{'} (x) < 0$ para toda $x \in (x_{0}, x_{0} + r)$ .

Y así por el criterio de la primera derivada tendríamos que $x_{0}$ es máximo local.

Por hipótesis tenemos que $f^{''} (x_{0}) < 0$ , lo que por definición de derivada sería:
$lim_{h \to 0} \frac{f^{'} (x_{0} + h) - f^{'} (x_{0})}{h} < 0$
Así sabemos que existe una $δ$ tal que para toda $h \in (- δ, δ)$ ocurre que:
$\frac{f^{'} (x_{0} + h) - f^{'} (x_{0})}{h} < 0$

Veamos qué ocurre en los siguientes dos casos:
Caso 1: $h < 0$ entonces tendríamos que $x_{0} + h < x_{0}$ y de la desigualdad anterior se seguiría que
$\begin{aligned} \frac{f^{'} (x_{0} + h) - f^{'} (x_{0})}{h} < 0 & \Rightarrow f^{'} (x_{0} + h) - f^{'} (x_{0}) > 0 \\ (donde f^{'} (x_{0}) = 0) & \Rightarrow f^{'} (x_{0} + h) > 0 \end{aligned}$

Caso 2: $h > 0$ se tiene que $x_{0} + h > x_{0}$ análogamente vemos que
$\begin{aligned} \frac{f^{'} (x_{0} + h) - f^{'} (x_{0})}{h} < 0 & \Rightarrow f^{'} (x_{0} + h) - f^{'} (x_{0}) < 0 \\ (donde f^{'} (x_{0}) = 0) & \Rightarrow f^{'} (x_{0} + h) < 0 \end{aligned}$

Concluyendo la prueba del inciso 2.

Detengámonos un momento a realizar la siguiente observación del teorema anterior:
Observación: si $f^{''} (x) = 0$ no podemos concluir nada, ya que el criterio no logra determinar si se trata de un máximo, un mínimo o ninguno de los anteriores. En este caso es necesario hacer uso de otros resultados como el Criterio de la primera derivada.

Esto sucede por ejemplo con la función $f (x) = x^{3}$ cuando $x_{0} = 0$ , ya que al evaluar su segunda derivada en $x_{0}$ obtenemos:
$f^{''} (x_{0}) = 0.$
Al ver la gráfica de la función cúbica notamos que en el punto $x_{0} = 0$ no tenemos un máximo local, así como no tenemos un mínimo local.

Ahora veamos que al considerar $f (x) = x^{4}$ con $x_{0} = 0$ y su segunda derivada evaluada en $x_{0}$ también ocurre que $f^{''} (x_{0}) = 0$ . Si recurrimos a visualizar su gráfica tenemos en este caso que $x_{0}$ es un mínimo local de $f$ . Un camino alterno para determinarlo podría ser utilizar el Criterio de la primera derivada visto en la entrada anterior.

De este modo después de aplicar el Criterio de la segunda derivada al obtener $f^{''} (x_{0}) = 0$ es necesario realizar un análisis más profundo valiéndonos de otros recursos y resultados.

Ejemplo

Utilizando el Criterio de la segunda derivada encuentra los máximos y mínimos de la siguiente función:
$f (x) = x^{3} - 3 x^{2} - 9 x + 1.$

Solución:
Paso 1: Obtenemos la primera derivada de la función
$\begin{aligned} f^{'} (x) & = 3 x^{2} - 6 x - 9 \\ = x^{2} - 2 x - 3 \\ = (x - 3) (x + 1) \\ ∴ f^{'} (x) & = (x - 3) (x + 1) . \end{aligned}$
Paso 2: Igualamos a cero la primera derivada para obtener los puntos críticos
$\begin{aligned} f^{'} (x) = 0 & \Leftrightarrow (x - 3) (x + 1) = 0 \\ \Leftrightarrow x - 3 = 0 & o (x + 1) = 0 \\ \Leftrightarrow x = 3 & o x = - 1 \end{aligned}$

Paso 3: Ahora obtenemos la segunda derivada de $f$
$f^{''} (x) = 2 x - 2.$

Paso 4: Sustituimos los valores de los puntos críticos obtenidos en el paso 2 y aplicamos el Criterio de la segunda derivada

Sustituimos $x = 3$ en $f^{''} (x)$ :
$f^{''} (3) = 2 (3) - 2 = 4$
El resultado obtenido nos dice que $f^{''} (3) > 0$ por lo que $f$ tiene un mínimo en $(3, - 26)$
Ahora para $x = - 1$ :
$f^{''} (- 1) = 2 (- 1) - 2 = - 4$
Vemos que $f^{''} (- 1) < 0$ obteniendo un máximo de $f$ en $(- 1, 6)$

Convexidad y concavidad

Definición (función convexa): Sea $f : [a, b] \to R$ una función. Decimos que $f$ es convexa en [a,b] si para cualesquiera $x, y \in [a, b]$ con $x < y$ se cumple que para todo $z \in [x, y]$ :
$f (z) \leq \frac{f (x) - f (y)}{x - y} (z - y) + f (y) .$

Lo que esta definición nos dice es que todos los puntos de la recta secante que une a $(y, f (y))$ con $(x, f (x))$ cuando $x < y$ se encuentran por arriba de la gráfica como se ve en la siguiente imagen.

Observación: Recordemos que, en el contexto de funciones y gráficas, una recta secante es una línea recta que intercepta a una curva en dos puntos distintos.

Una definición equivalente sería que para cualquier $α \in (0, 1)$ se cumple:
$f (α x + (1 - α) y) \leq α f (x) + (1 - α) f (y) .$

Para ver que la definición implica esto, notemos que si $z = α x + (1 - α) y$ con $α \in (0, 1)$ , entonces $z \leq y$ y $z \geq x$ . Así, por definición, tendríamos que

$\begin{aligned} f (α x + (1 - α) y) & = f (z) \\ \leq \frac{f (x) - f (y)}{x - y} (z - y) + f (y) \\ = \frac{f (x) - f (y)}{x - y} (α x - α y) + f (y) \\ = α (f (x) - f (y)) + f (y) \\ = α f (x) + (1 - α) f (y), \end{aligned}$

como afirmamos. Por otro lado, si se cumple lo que afirmamos que es una equivalencia, entonces cualquier $z \in (x, y)$ puede ser escrito como $z = α x + (1 - α) y$ con $α \in (0, 1)$ (esto se puede probar, por ejemplo, por teorema del valor intermedio, pues $α \mapsto α x + (1 - α) y$ es continua, en $α = 0$ vale $y$ y en $α = 1$ vale $x$ ). Así, suponiendo la segunda versión tendríamos

$\begin{aligned} f (z) & = f (α x + (1 - α) y) \\ \leq α f (x) + (1 - α) f (y) \\ = \frac{f (x) - f (y)}{x - y} (z - y) + f (y), \end{aligned}$

en donde en la última igualdad se hacen cuentas similares a las hechas arriba.

Otras definiciones son las siguientes:

Definición (función estrictamente convexa): Sea $f : [a, b] \to R$ una función. Se dice que $f$ es estrictamente convexa si cumple la desigualdad:
$f (α x + (1 - α) y) < α f (x) + (1 - α) f (y),$ para $α \in (0, 1)$ .
Definición (función estrictamente cóncava): Decimos que $f$ es estrictamente cóncava si $- f$ es estrictamente convexa.
Definición (función cóncava): Decimos que $f$ es cóncava si $- f$ es convexa.

La derivada y la convexidad

Teorema: Consideremos $f : (a, b) \to R$ una función. Si $f^{'} (x)$ es no decreciente en $(a, b)$ entonces $f$ es convexa en $(a, b)$ .

Demostración:

Consideremos $x, y \in (a, b)$ . Queremos demostrar que para cualquier $α \in (0, 1)$ se cumple la desigualdad:
$f (α x + (1 - α) y) \leq α f (x) + (1 - α) f (y) .$

Así tomemos $α_{0} \in [0, 1]$ y probemos que:
$f (α_{0} x + (1 - α_{0}) y) \leq α_{0} f (x) + (1 - α_{0}) f (y) .$

Por el teorema del valor medio para la derivada tenemos que existe $p \in (x, z)$ donde podemos considerar $z = α_{0} x + (1 - α_{0}) y$ tal que:
$f^{'} (p) = \frac{f (z) - f (x)}{z - x} .$
Análogamente existe $q \in (z, y)$ que:
$f^{'} (q) = \frac{f (y) - f (z)}{y - z} .$

Por hipótesis vemos que:
$f^{'} (p) \leq f^{'} (q) .$
Es decir:
$\frac{f (z) - f (x)}{z - x} \leq \frac{f (y) - f (z)}{y - z} .$

Y como $z = α_{0} x + (1 - α_{0}) y$ :
$\begin{aligned} \Rightarrow \frac{f (z) - f (y)}{(α_{0} - 1) x + (1 - α_{0}) y} \leq \frac{f (y) - f (z)}{y - α_{0} x - (1 - α_{0}) y} \\ \Rightarrow \frac{f (z) - f (y)}{(y - x) (1 - α_{0})} \leq \frac{f (y) - f (z)}{α_{0} (y - x)} \\ \Rightarrow α_{0} (f (z) - f (x)) \leq (1 - α_{0}) (f (y) - f (z)) \end{aligned}$
Por lo tanto si desarrollamos lo anterior:
$\begin{aligned} α_{0} f (z) + (1 - α_{0}) f (z) & \leq α_{0} f (x) + (1 - α_{0}) f (y) \\ ∴ f (z) & \leq α_{0} f (x) + (1 - α_{0}) f (y) \end{aligned}$
Recordando que $z = α_{0} x + (1 - α_{0}) y$ concluimos que:
$f (α_{0} x + (1 - α_{0})) \leq α_{0} f (x) + (1 - α_{0}) f (y) .$

Una consecuencia del teorema anterior es el siguiente corolario:
Corolario: Sea $f : (a, b) \to R$ una función.

Si $f^{''} (x) \geq 0$ entonces $f$ es convexa.
Si $f^{''} (x) \leq 0$ entonces $f$ es cóncava.

Así vemos que la segunda derivada nos puede ayudar a determinar los intervalos donde una función es convexa o cóncava.

Puntos de inflexión de una función

Definición (punto de inflexión): Decimos que $x_{0}$ es un punto de inflexión si en él la función cambia de convexa a cóncava ó de cóncava a convexa.
Para poder identificarlos usando la derivada tenemos que si $f^{''} (x_{0}) = 0$ y $f^{''} (x_{0}) \neq 0$ entonces $x_{0}$ es un punto de inflexión.

En el siguiente ejemplo utilizaremos este criterio para identificar los puntos de inflexión de la función vista en el ejercicio anterior.

Ejemplo

Recordemos que estamos trabajando con la función:
$f (x) = x^{3} - 3 x^{2} - 9 x + 1 .$
Cuyas segunda y tercera derivada son:
$f^{''} (x) = 2 x - 2$
$f^{'''} (x) = 2$
Para identificar a sus puntos de inflexión igualaremos a cero su segunda derivada y encontraremos las raíces de la misma:
$\begin{aligned} f^{''} (x) = 0 & \Rightarrow 2 x - 2 = 0 \\ \Rightarrow x - 1 = 0 \\ \Rightarrow x = 1 \end{aligned}$
Sustituimos $x = 1$ en la función original:
$f (1) = (1)^{3} - 3 (1)^{2} - 9 (1) + 1 = - 10$
Además, como $f^{'''} ((1) = 2$ , podemos concluir que $f$ tiene un punto de inflexión en $(1, - 10)$ .

Ahora para definir donde la función es convexa debemos resolver la siguiente desigualdad:
$\begin{aligned} f^{''} (x) > 0 & \Rightarrow x - 1 > 0 \\ \Rightarrow x > 1 \end{aligned}$
Así $f$ es convexa en $(1, \infty)$

Y para ver donde es cóncava utilizamos:
$\begin{aligned} f^{''} (x) < 0 & \Rightarrow x - 1 < 0 \\ \Rightarrow x < 1 \end{aligned}$
Por lo que $f$ es cóncava en $(- \infty, 1)$

Más adelante

Ahora que hemos visto dos criterios importantes haciendo uso de la derivada para localizar máximos y mínimos de una función, en la siguiente entrada donde hablaremos de problemas de optimización, será esencial poder identificarlos.

Tarea moral

Para cada una de las siguientes funciones obtén:

Máximos y mínimos.
Intervalos donde crece y decrece la función.
Intervalos donde es convexa o cóncava.
Puntos de inflexión.
Gráfica.

$f (x) = x^{2} + \frac{1}{x^{2}}$
$f (x) = x^{3} (x + 2)$
$f (x) = \sqrt{x^{2} + 36}$
$f (x) = - 2 x^{3} + 9 x^{2} + 60 x$

Entradas relacionadas

Ir a: Cálculo Diferencial e Integral I
Entrada anterior del curso: Cálculo Diferencial e Integral I: Localización de máximos y mínimos. Monotonía de funciones.
Entrada siguiente del curso: Cálculo Diferencial e Integral I: Problemas de optimización.
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Localización de máximos y mínimos. Monotonía de funciones

Por Karen González Cárdenas

Deja un comentario

Introducción

En cursos de Cálculo en el bachillerato, posiblemente resolviste ejercicios en los cuales te solicitaban hallar los puntos críticos de una función y realizar la gráfica de la misma basándote en ellos.
Recordemos primero que un punto crítico $x$ de una función $f$ es aquel que al evaluarlo en la derivada de $f$ nos da la siguiente igualdad:
$f^{'} (x) = 0.$

Y que en el conjunto de estos puntos críticos se encontraban los máximos y mínimos de la función $f$ .
En esta entrada daremos las definiciones formales correspondientes y veremos los Criterios de las derivadas para identificarlos. También veremos resultados en los que, haciendo uso de la derivada, podremos determinar si una función es creciente o decreciente en un intervalo.

Máximo y mínimo global

Definición: Sea $f : D_{f} \subseteq R \to R$ una función y $x_{0} \in D_{f}$ . Decimos que en $x_{0}$ se alcanza:

Un máximo global si para toda $x \in D_{f}$ se cumple que:
$f (x) \leq f (x_{0}) .$
Un mínimo global si para toda $x \in D_{f}$ se cumple que:
$f (x_{0}) \leq f (x) .$

Máximo y mínimo local

Definición: Consideremos a una función $f$ continua en un intervalo $I$ y $x_{0} \in (x_{0} - r, x_{0} + r) \subseteq I$ con $r \in R^{+}$ y tenemos que existe $f (x_{0})$ decimos que:

$x_{0}$ es un máximo local de $f \Leftrightarrow$ existe $r > 0$ tal que para todo $x \in (x_{0} - r, x_{0} + r) \subseteq D_{f}$ ocurre que:
$f (x) \leq f (x_{0}) .$
$x_{0}$ es un mínimo local de $f \Leftrightarrow$ existe $r > 0$ tal que para todo $x \in (x_{0} - r, x_{0} + r) \subseteq D_{f}$ ocurre que:
$f (x_{0}) \leq f (x) .$
$x_{0}$ no es máximo ni mínimo si existen $x_{1}, x_{2}$ tales que para toda $r > 0$ y para cualquier $x \in (x_{0} - r, x_{0} + r)$ ocurre que:
$f (x_{1}) < f (x_{0}) < f (x_{2}) .$

En la imagen anterior vemos que el punto $A$ es un máximo de la función y $B$ un mínimo.

La derivada y los puntos críticos

Teorema: Consideremos una función $f$ continua en un intervalo $I$ y es derivable en el punto $x_{0} \in (x_{0} - r, x_{0} + r) \subseteq I$ .

Si tenemos que $x_{0}$ es un máximo o un mínimo local de $f \Rightarrow f^{'} (x_{0}) = 0$ .

Demostración: Tomemos $x_{0}$ máximo local de $f$ , así por definición tenemos que existe $r_{1} > 0$ tal que para cualquier $x \in (x_{0} - r_{1}, x_{0} + r_{1})$ ocurre que:
$f (x) \leq f (x_{0}) .$
O bien, si $x_{0}$ mínimo local de $f$ tenemos que existe $r_{1} > 0$ tal que para cualquier $x \in (x_{0} - r_{1}, x_{0} + r_{1})$ ocurre que:
$f (x_{0}) \leq f (x) .$
Consideremos ahora $h$ tal que:
$| h | \leq r_{2} = min {r, r_{1}} .$
Veremos el caso en que $x_{0}$ es máximo local de $f$ .
Caso 1: Supongamos que $x_{0}$ es máximo.
Si tenemos que $h > 0$ se sigue que:
$\begin{aligned} f (x_{0} + h) < f (x_{0}) & \Rightarrow f (x_{0} + h) - f (x_{0}) < 0 \\ \Rightarrow \frac{f (x_{0} + h) - f (x_{0})}{h} < 0 \\ \Rightarrow lim_{h \to 0^{+}} \frac{f (x_{0} + h) - f (x_{0})}{h} \leq 0 \end{aligned}$

Ya que $f$ es derivable en $x_{0}$ entonces podemos afirmar la siguiente igualdad:
$lim_{h \to 0^{+}} \frac{f (x_{0} + h) - f (x_{0})}{h} = f^{'} (x_{0}) .$
$∴ f^{'} (x_{0}) \leq 0.$

Ahora bien, si tenemos que $h < 0$ tenemos que:
$\begin{aligned} f (x_{0} + h) - f (x_{0}) < 0 & \Rightarrow \frac{f (x_{0} + h) - f (x_{0})}{h} > 0 \\ \Rightarrow lim_{h \to 0^{-}} \frac{f (x_{0} + h) - f (x_{0})}{h} \geq 0 \end{aligned}$
$∴ f^{'} (x_{0}) \geq 0.$
$∴ 0 \leq f^{'} (x_{0}) \leq 0.$

Y así concluimos que $f^{'} (x_{0}) = 0.$

El Caso 2 considerando ahora que $x_{0}$ es mínimo se quedará como ejercicio de Tarea moral, para realizar la prueba se procede de manera análoga al caso que ya vimos.

Gráficamente el resultado anterior se vería como sigue:

donde en el intervalo en el que se encuentra el punto $A$ la recta tangente a dicho punto tiene pendiente cero, es decir, es una recta horizontal. Observamos que para el intervalo (representado por la franja rosa) en el que se encuentra el punto $B$ tenemos una situación similar.

La derivada y la monotonía de las funciones

Teorema: Consideremos $f$ una función e $I$ un intervalo.

Si $f^{'} (x) > 0$ para todo $x \in I \Rightarrow f$ es creciente en $I$ .
Si $f^{'} (x) \geq 0$ para todo $x \in I \Rightarrow f$ es no decreciente en $I$ .
Si $f^{'} (x) < 0$ para todo $x \in I \Rightarrow f$ es decreciente en $I$ .
Si $f^{'} (x) \leq 0$ para todo $x \in I \Rightarrow f$ es no creciente en $I$ .

Demostración 1:

Queremos probar que para cualesquiera $x_{1}, x_{2} \in I$ donde si $x_{1} < x_{2}$ entonces:
$f (x_{1}) < f (x_{2}) .$

Así tomemos $x_{1}, x_{2}$ en el intervalo $I$ con $x_{1} < x_{2}$ . Veamos que $[x_{1}, x_{2}] \subseteq I$ y que $f$ es derivable en $(x_{1}, x_{2}) \subseteq I$ . Y además tenemos que $f$ es continua en $[x_{1}, x_{2}] \subseteq I$ , aplicando el Teorema del valor medio para la derivada:
$\exists α \in (x_{1}, x_{2})$ tal que $f^{'} (α) = \frac{f (x_{2}) - f (x_{1})}{x_{2} - x_{1}}$ .
Por hipótesis tenemos que:
$f^{'} (α) = \frac{f (x_{2}) - f (x_{1})}{x_{2} - x_{1}} > 0.$
Debido a que también supusimos $x_{2} - x_{1} > 0$ para que se cumpla la desigualdad anterior necesariamente debe ocurrir que:
$f (x_{2}) - f (x_{1}) > 0 \Rightarrow f (x_{2}) > f (x_{1}) .$

Criterio de la primera derivada

Teorema (Criterio de la primera derivada): Si $f^{'} (x_{0}) = 0$ y existe $r > 0$ tal que:

Para todo $x \in (x_{0} - r, x_{0})$ , $f^{'} (x) < 0$ y para todo $x \in (x_{0}, x_{0} + r)$ , $f^{'} (x) > 0$
$\Rightarrow x_{0}$ es mínimo local de $f$ .
Para todo $x \in (x_{0} - r, x_{0})$ , $f^{'} (x) > 0$ y para todo $x \in (x_{0}, x_{0} + r)$ , $f^{'} (x) < 0$
$\Rightarrow x_{0}$ es máximo local de $f$ .

Demostración 1:

Sea $x \in (x_{0} - r, x_{0})$ por hipótesis tenemos que $f^{'} (x) < 0$ . Aplicando el teorema anterior afirmamos que $f$ es decreciente en $(x_{0} - r, x_{0})$ , así para cualquier $x < x_{0}$ en $(x_{0} - r, x_{0})$ :
$f (x) > f (x_{0}) .$

Ahora tomando $x \in (x_{0}, x_{0} + r)$ tenemos que $f^{'} (x) > 0$ . Y por el teorema anterior sabemos que $f$ es creciente en el intervalo $(x_{0}, x_{0} + r)$ . Por definición para cualquier $x > x_{0}$ en $(x_{0}, x_{0} + r)$ ocurre que:
$f (x_{0}) < f (x) .$
De lo anterior podemos concluir que para toda $x \in (x_{0} - r, x_{0}) \cup (x_{0}, x_{0} + r) = (x_{0} - r, x_{0} + r)$ se cumple la desigualdad:
$f (x_{0}) < f (x) .$
que es justo la definición de $x_{0}$ mínimo local de $f$ .

A continuación veremos ejemplos donde aplicaremos los teoremas anteriores para localizar los máximos y mínimos de una función, como los intervalos donde es creciente o decreciente.

Ejemplo 1

Encuentra los puntos críticos de la siguiente función y determina si se trata de un máximo o un mínimo:
$f (x) = (x - 1)^{2} (x + 1)^{3}$

Solución:

Para encontrarlos seguiremos los siguientes pasos:
Paso 1: Hallamos la primera derivada de la función $f$ .
$\begin{aligned} f^{'} (x) & = 2 (x - 1) (x + 1)^{3} + 3 (x + 1)^{2} (x - 1)^{2} \\ = (x - 1) [2 (x + 1)^{3} + 3 (x + 1)^{2} (x - 1)] \\ = (x - 1) (x + 1)^{2} [2 (x + 1) + 3 (x - 1)] \\ = (x - 1) (x + 1)^{2} [2 x + 2 + 3 x + 3] \\ = (x - 1) (x + 1)^{2} (5 x - 1) \\ ∴ f^{'} (x) & = (x - 1) (x + 1)^{2} (5 x - 1) \end{aligned}$

Paso 2: Igualamos la derivada a cero para encontrar los puntos críticos.
$f^{'} (x) = 0 \Leftrightarrow (x - 1) (x + 1)^{2} (5 x - 1) = 0$
El producto anterior lo cumple cuando:
$\begin{aligned} (x + 1)^{2} = 0 & o 5 x - 1 = 0 & o x - 1 = 0 \\ \sqrt{(x + 1)^{2}} = \sqrt{0} & o 5 x = 1 & o x = 1 \\ x + 1 = 0 & o x = \frac{1}{5} \\ x = - 1 \end{aligned}$

Por lo que debemos determinar para $x = 1$ , $x = - 1$ y $x = \frac{1}{5}$ si se trata de un máximo, un mínimo o ninguno de los dos.

Paso 3: Para determinar si es un máximo o mínimo, aplicando el Criterio de la primera derivada debemos sustituir en la primera derivada un valor $x_{1} < x$ para determinar si $f^{'} (x_{1})$ es positiva o negativa. De igual modo debemos evaluar una $x < x_{2}$ y obtener si $f^{'} (x_{2})$ es positiva o negativa.

Comencemos con $x = 1$ :
Si tomamos $x < 1$ y sustituimos en $f^{'} (x) = 5 (x - 1) (x + 1)^{2} (x - \frac{1}{5})$ a $x_{1} = \frac{1}{2}$ en la derivada
$\begin{aligned} f^{'} (\frac{1}{2}) & = 5 (\frac{1}{2} - 1) {(\frac{1}{2} + 1)}^{2} (\frac{1}{2} - \frac{1}{5}) \\ (que es negativo) & = 5 (- \frac{1}{2}) {(\frac{3}{2})}^{2} (\frac{3}{10}) \end{aligned}$
Ahora para $x > 1$ evaluamos $x_{2} = 2$
$\begin{aligned} f^{'} (2) & = 5 (2 - 1) (2 + 1)^{2} (2 - \frac{1}{5}) \\ (que es positivo) & = 5 (1) (3)^{2} (\frac{9}{5}) \end{aligned}$
Ya que la derivada pasó de ser negativa a positiva tenemos que cuando $x = 1$ la función tiene un mínimo.
$∴ p_{1} = (1, 0)$ es mínimo de $f$ .

Continuemos con $x = - 1$ :
Para $x < - 1$ tomaremos $x_{1} = - 2$ .
$\begin{aligned} f^{'} (- 2) & = 5 (- 2 - 1) (- 2 + 1)^{2} (- 2 - \frac{1}{5}) \\ (que es positivo) & = 5 (- 3) (- 1)^{2} (- \frac{11}{5}) \end{aligned}$

Y para $x > - 1$ consideramos ahora $x_{2} = - \frac{1}{2}$ .
$\begin{aligned} f^{'} (- \frac{1}{2}) & = 5 {(- \frac{1}{2} - 1)}^{2} (- \frac{1}{2} - \frac{1}{5}) \\ (que es positivo) & = 5 (- \frac{3}{2}) {(\frac{1}{2})}^{2} (- \frac{7}{10}) \end{aligned}$

Debido a que la derivada no presenta cambio de signo, cuando $x = - 1$ no es máximo ni mínimo.

Finalmente para $x = \frac{1}{5}$ análogamente procedemos:
Cuando $x < \frac{1}{5}$ sustituiremos $x_{1} = \frac{1}{6}$ .
$\begin{aligned} f^{'} (\frac{1}{6}) & = 5 (\frac{1}{6} - 1) {(\frac{1}{6} + 1)}^{2} (\frac{1}{6} - \frac{1}{5}) \\ (que es positivo) & = 5 (- \frac{5}{6}) {(\frac{7}{6})}^{2} (- \frac{1}{30}) \end{aligned}$

Ahora bien para $x > \frac{1}{5}$ evaluaremos $x_{2} = \frac{1}{2}$ .
$\begin{aligned} f^{'} (\frac{1}{2}) & = 5 (\frac{1}{2} - 1) {(\frac{1}{2} + 1)}^{2} (\frac{1}{2} - \frac{1}{5}) \\ (que es negativo) & = 5 (- \frac{1}{2}) (\frac{3}{2}) (\frac{3}{10}) \end{aligned}$

Vemos que la derivada pasó de ser positiva a ser negativa, por lo tanto, cuando $x = \frac{1}{5}$ la función $f$ tiene un máximo.
$∴ p_{2} = (0.2, 1.10)$ es un máximo de $f$ .

Ejemplo 2

Hallar los intervalos donde es creciente o decreciente la siguiente función:
$f (x) = 4 x^{3} + 3 x^{2} - 6 x .$

Solución:
Comenzaremos derivando la función y simplificando
$\begin{aligned} f^{'} (x) & = 12 x^{2} + 6 x - 6 \\ = 6 x^{2} + x - 1 \\ = (x - \frac{1}{2}) (x + 1) \end{aligned}$

Sabemos que cuando $f^{'} (x) > 0$ la función es creciente, por ello veremos qué valores satisfacen la siguiente desigualdad:
$(x - \frac{1}{2}) (x + 1) > 0.$
El producto anterior cumple ser positivo cuando
Caso 1:
$\begin{aligned} x - \frac{1}{2} > 0 & y x + 1 > 0 \\ x > \frac{1}{2} & y x > - 1 \end{aligned}$
Por lo que el intervalo solución para este caso es: $(\frac{1}{2}, \infty)$ .

Caso 2:
$\begin{aligned} x - \frac{1}{2} < 0 & y x + 1 < 0 \\ x < \frac{1}{2} & y x < - 1 \end{aligned}$
Así el intervalo solución es: $(- \infty, - 1)$ .

Concluimos que los intervalos donde $f$ es creciente son:
$(- \infty, - 1) \cup (\frac{1}{2}, \infty) .$

Para encontrar donde la función es decreciente debemos trabajar con la desigualdad $f^{'} (x) < 0$ , que sería:
$(x - \frac{1}{2}) (x + 1) < 0.$
Lo anterior se cumple en los siguientes casos:
Caso 3:
$\begin{aligned} x - \frac{1}{2} > 0 & y x + 1 < 0 \\ x > \frac{1}{2} & y x < - 1 \end{aligned}$
Vemos que la solución de este caso es vacía.

Caso 4:
$\begin{aligned} x - \frac{1}{2} < 0 & y x + 1 > 0 \\ x < \frac{1}{2} & y x > - 1 \end{aligned}$
El intervalo que cumple lo anterior es $(- 1, \frac{1}{2})$ .

De los casos anteriores tenemos que $f$ es decreciente en el intervalo:
$(- 1, \frac{1}{2})$

Más adelante

En la siguiente entrada seguiremos trabajando con los máximos y mínimos de funciones, por lo que te presentaremos una herramienta más para poder localizarlos: el Criterio de la segunda derivada. También veremos cómo determinar las regiones de concavidad o convexidad de una función y sus puntos de inflexión.

Tarea moral

Da la demostración del teorema para el caso en que $x_{0}$ es un mínimo local de $f$ .
Prueba los siguientes puntos:
- Si $f^{'} (x) \geq 0$ para todo $x \in I \Rightarrow f$ es no decreciente en $I$ .
- Si $f^{'} (x) < 0$ para todo $x \in I \Rightarrow f$ es decreciente en $I$ .
- Si $f^{'} (x) \leq 0$ para todo $x \in I \Rightarrow f$ es no creciente en $I$ .
Determina si los siguientes enunciados son verdaderos o falsos. De ser verdadero da la demostración correspondiente, de lo contrario da un contraejemplo:
- Si $f$ es una función creciente, derivable y continua en un intervalo $I \Rightarrow f^{'} (x) > 0$ para toda $x \in I$ .
- Si $f$ es una función estrictamente creciente, continua y derivable en $I \Rightarrow f^{'} (x) > 0$ para toda $x \in I$ .
Realiza la gráfica de la función:
$f (x) = \frac{1}{(x - 1)^{2}} + 1.$
Determinando los intervalos donde $f$ es creciente o decreciente.
Señalando si es que existen:
- máximos y mínimos (locales y globales).
- los valores $x$ donde $f (x) = 0$ .
- $lim_{x \to \infty^{+}} f (x)$ .
- $lim_{x \to \infty^{-}} f (x)$ .

Entradas relacionadas

Ir a: Cálculo Diferencial e Integral I
Entrada anterior del curso: Cálculo Diferencial e Integral I: Rectas tangente y normal a una curva.
Entrada siguiente del curso: Cálculo Diferencial e Integral I: Localización de máximos y mínimos. Regiones de convexidad y puntos de inflexión.
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Rectas tangente y normal a una curva

Por Karen González Cárdenas

Deja un comentario

Introducción

En la unidad anterior vimos la teoría relacionada a las funciones derivables. A lo largo de esta última parte del curso, veremos una serie de aplicaciones de la derivada en distintos ámbitos. Esperamos que te parezcan interesantes los ejemplos que aquí expondremos y la relación del Cálculo en problemáticas de otras áreas. Comenzaremos con obtener la recta tangente y normal de una función en un punto dado.

¿Qué dice la geometría?

Recordemos algunos conceptos geométricos para entrar en contexto:
Decimos que una recta $T$ es tangente si toca a una curva en un sólo punto. Y que una recta $N$ es normal si es perpendicular a la recta tangente en el punto de tangencia.

$T$ es la recta tangente en el punto $p$
$N$ es la recta normal en $p$

En los cursos de geometría probablemente te encontraste con la siguiente ecuación para definir a una recta:
$y - y_{1} = m (x - x_{1})$
ésta es conocida como la forma punto-pendiente.

Vemos que gráficamente estamos considerando un punto $(x_{1}, y_{1})$ sobre la recta y decimos que un punto cualquiera $(x, y)$ se encuentra también sobre la recta si cumple la igualdad anterior.

Recordando…

A principios de la unidad pasada vimos que una función $f$ es derivable en un punto $x_{0}$ si existe el siguiente límite:
$lim_{x \to x_{0}} \frac{f (x) - f (x_{0})}{x - x_{0}} = f^{'} (x_{0}) .$

Y que además la interpretación geométrica de dicho límite es justo la pendiente de la recta tangente a la gráfica de nuestra función $f$ en un $(x_{0}, f (x_{0}))$ .
Con ayuda de este concepto y la definición vista en la sección anterior, vemos que la recta que pasa por el punto $(x_{0}, f (x_{0}))$ y que es tangente a la gráfica sería:
$\begin{aligned} y - y_{1} & = m (x - x_{1}) \\ y - f (x_{0}) & = f^{'} (x_{0}) (x - x_{0}) \\ y & = f^{'} (x_{0}) (x - x_{0}) + f (x_{0}) \end{aligned}$
donde $m = f^{'} (x_{0})$ y consideramos $(x_{1}, y_{1}) = (x_{0}, f (x_{0}))$ .

Definición de la recta tangente

Motivados por lo anterior tenemos la siguiente definición:
Definición (recta tangente): Sea $f$ una función derivable en un punto $x_{0}$ . Definimos a la recta tangente a la gráfica de $f$ en el punto $(x_{0}, f (x_{0}))$ como:
$T (x) = f^{'} (x_{0}) (x - x_{0}) + f (x_{0}) .$

Esta definición es la que estaremos usando en todos los ejercicios de esta entrada por lo que recomendamos tenerla presente. Pasaremos ahora a definir la recta normal a la gráfica de $f$ en el punto $(x_{0}, f (x_{0}))$ .

Definición de la recta normal

Como ya vimos que geométricamente la recta normal es perpendicular a la recta tangente, modificaremos la pendiente a la definición anterior tomando $m = - \frac{1}{f^{'} (x_{0})}$ con $f^{'} (x_{0}) \neq 0$ :
Definición (recta normal): Tomando $f$ una función derivable en un punto $x_{0}$ . Definimos a la recta normal a la gráfica de $f$ en el punto $(x_{0}, f (x_{0}))$ con la ecuación:
$N (x) = - \frac{1}{f^{'} (x_{0})} (x - x_{0}) + f (x_{0}) .$

Con ambas rectas definidas pasaremos a resolver algunos ejercicios.

Ejemplo 1

Encuentra la recta tangente y normal de la función:
$f (x) = x^{3} + 2 x^{2} - x + 2$
en el punto $(4, 94)$ .
Solución:
Comenzaremos por obtener la derivada de $f (x)$ haciendo uso de las reglas de derivación:
$f^{'} (x) = 3 x^{2} + 4 x - 1.$

Para obtener la pendiente en el punto indicado debemos sustituir $x = 4$ , así:
$\begin{aligned} f^{'} (4) & = 3 (4)^{2} + 4 (4) - 1 \\ = 48 + 16 - 1 \\ = 63 \end{aligned}$

Ahora comenzamos sustituyendo lo anterior en la definición de recta tangente:
$\begin{aligned} T (x) & = 63 \cdot (x - 4) + 94 \\ = 63 x - 252 + 94 \\ = 63 x - 158 \end{aligned}$
$∴ T (x) = 63 x - 158 .$

Finalmente sustituyendo en la definición de la recta normal:
$\begin{aligned} N (x) & = - \frac{1}{63} \cdot (x - 4) + 94 \\ = - \frac{x}{63} + \frac{4}{63} + 94 \\ = - \frac{x}{63} + \frac{5926}{63} \end{aligned}$
$∴ N (x) = - \frac{x}{63} + \frac{5926}{63} .$

Ejemplo 2

Encuentra la recta tangente y normal con $x_{0} = 2$ de la función:
$f (x) = 3 x^{2} - 5 x + 6.$
Solución:
Comenzamos por sustituir $x_{0} = 2$ para obtener el punto $p$ por donde pasarán ambas rectas:
$\begin{aligned} f (2) & = 3 (2)^{2} - 5 (2) + 6 \\ = 12 - 10 + 6 \\ = 8 \end{aligned}$
$∴ p = (2, 8) .$
Ahora pasemos a obtener la pendiente derivando la función y sustituyendo $x_{0} = 2$ :
$f^{'} (x) = 6 x - 5 \Rightarrow f^{'} (2) = 6 (2) - 5 = 12 - 5 = 7.$

Procedamos a sustituir en las definiciones para la tangente y la normal:
$\begin{aligned} T (x) & = 7 (x - 2) + 8 & N (x) & = - \frac{1}{7} (x - 2) + 8 \\ = 7 x - 14 + 8 & = - \frac{x}{7} + \frac{2}{7} + 8 \\ = 7 x - 6 & = - \frac{x}{7} + \frac{58}{7} \end{aligned}$
Así concluimos que:
$\begin{aligned} T (x) & = 7 x - 6 \\ N (x) & = - \frac{x}{7} + \frac{58}{7} \end{aligned}$

Ejemplo 3

Hallar la recta tangente y normal de la función:
$f (x) = \sqrt{- x}$
en el punto $p = (- 9, 3)$ .
Solución:
Procederemos a derivar la función haciendo uso de la Regla de la cadena:
$\begin{aligned} f^{'} (x) & = \frac{1}{2} (- x)^{\frac{1}{2} - 1} \cdot (- 1) \\ = - \frac{1}{2} (- x)^{- \frac{1}{2}} \\ = - \frac{1}{2 \sqrt{- x}} \end{aligned}$

Obtenemos la pendiente al sustituir $x_{0} = - 9$ :
$\begin{aligned} f^{'} (- 9) & = - \frac{1}{2 \sqrt{- (- 9)}} \\ = - \frac{1}{2 \sqrt{9}} \\ = - \frac{1}{6} \end{aligned}$

Ahora hallamos la recta tangente y normal sustituyendo $f^{'} (- 9) = - \frac{1}{6}$ :
$\begin{aligned} T (x) & = - \frac{1}{6} (x - (- 9)) + 3 & N (x) & = - \frac{1}{- \frac{1}{6}} (x - (- 9)) + 3 \\ = - \frac{1}{6} (x + 9) + 3 & = 6 (x + 9) + 3 \\ = - \frac{x}{6} - \frac{3}{2} + 3 & = 6 x + 54 + 3 \\ = - \frac{x}{6} + \frac{3}{2} & = 6 x + 57 \end{aligned}$

Por lo que finalmente tenemos:
$\begin{aligned} T (x) & = - \frac{x}{6} + \frac{3}{2} \\ N (x) & = 6 x + 57 \end{aligned}$

Más adelante

En la siguiente entrada veremos cómo encontrar máximos y mínimos de una función. Por lo tanto, definiremos dichos conceptos y probaremos algunos resultados que nos brindarán los criterios necesarios, haciendo uso de la derivada, para identificarlos.

Tarea moral

Encuentra la recta tangente y normal en cada uno de los incisos:

$f (x) = 2 x^{3} + 3 x^{2} + 4 x - 2$ con $x_{0} = 2$ .
$f (x) = x^{3} - 3 x$ en $p = (2, 2)$ .
$f (x) = 4 x^{2}$ en $p = (2, 16)$ .
$f (x) = s e n (\frac{π}{2} - x)$ en $p = (\frac{π}{3}, \frac{1}{2})$ .
$f (x) = \frac{x + 1}{x - 1}$ en $p = (2, 3)$ .

Entradas relacionadas

Ir a: Cálculo Diferencial e Integral I
Entrada anterior del curso: Cálculo Diferencial e Integral I: Regla de L’Hôpital.
Entrada siguiente del curso: Cálculo Diferencial e Integral I: Localización de máximos y mínimos. Monotonía de funciones.
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»