Archivo del Autor: Armando Arzola Pérez

Geometría Moderna II: Inversión de Rectas y Circunferencias

Por Armando Arzola Pérez

Deja un comentario

2.2 Inversión de Rectas y Circunferencias

Introducción

De la definición de Inversión se tiene la siguiente propiedad, se tienen $P$ y $P’$ dos puntos inversos respecto a la circunferencia $C(O,r)$, y cada uno de estos describe una curva, $P$ describe a $C$ y $P’$ describe a $C’$. Estas curvas son inversas una de la otra, se les llama mutuamente inversas.

Propiedad (Curvas de Inversión)

Se tienen 2 curvas $C$ y $C’$ inversas una de la otra, las cuales se intersecan, esto lo hacen sobre la circunferencia de Inversión, debido a que el punto en común debe ser su propio inverso, y el inverso de un punto en la $C(O,r)$ es el propio punto en la circunferencia de inversión.
Dado lo anterior se puede ver la inversión aplicada a 2 objetos geométricos: Rectas y Circunferencias.

Teorema (Inversión en Recta que pasa por O)

Sea $C(O,r)$ una circunferencia de inversión y $L$ una recta que pasa por $O$, entonces el inverso de $L$ respecto a $C(O,r)$ es el mismo $L$.

Demostración

Tenemos una circunferencia $C(O,r)$ y $L$ una recta por $O$, además todo punto $P$ en $L$ tiene su inverso $P’$ tal que $O,P$ y $P’$ son colineales entonces $OP \times OP’ =r^2$.

Inversión respecto a una recta que pasa por O.

Por lo cual los inversos de los puntos de $L$, también están en la misma recta $L$.
Por lo tanto, $L$ su inverso es el mismo $L$ $_\blacksquare$

Teorema (Inversión en Recta que no pasa por O)

Sea $C(O,r)$ una circunferencia de inversión y $L$ una recta que no pasa por $O$, entonces el inverso de $L$ respecto a $C$ es una circunferencia que pasa por $O$. Recíprocamente, el inverso de una circunferencia que pasa por el centro de inversión es una recta que no pasa por el centro de inversión.

Demostración

Inversión respecto a una recta que no pasa por O.

Sea $P$ el pie de la perpendicular desde $O$ a $L$ y sea $Q \neq P$, donde $Q \in L$ y de estos obtenemos $P’$ y $Q’$ los inversos respecto a $C$ de $P$ y $Q$ respectivamente.

$\Rightarrow OP \times OP’ =r^2$ y $OQ \times OQ’=r^2$

$\Rightarrow OP \times OP’ = OQ \times OQ’$

$\Rightarrow \frac{OP}{OQ’} = \frac{OQ}{OP’}$

$\Rightarrow \triangle OQ’P’ \approx \triangle OPQ$

Esto ya que comparten 2 lados proporcionales y un ángulo en común $\angle O$.
Ahora $\triangle OPQ$ es rectángulo, entonces $\triangle OQ’P’$ es rectángulo, por lo cual $OP’$ es un diámetro de una circunferencia que pasa por $Q’$.

Análogamente, si tuviéramos un $R \in L$, $R \neq P$ y $R \neq Q$, su inverso $R’$ cumplirá $\frac{OP}{OR’} = \frac{OR}{OP’}$, con lo que $\triangle OPR \approx \triangle OR’P’$, por lo cual $\triangle OR’P’ $ es rectángulo, como $OP’$ es fijo se sigue que la circunferencia del diámetro $OP’$ que pasa por $Q’$ también pasa por $R’$.
Por lo tanto, el inverso de $L$ respecto a $C$ es $C_1$ una circunferencia que pasa por $O$ $_\blacksquare$

Inversamente, si $Q’$ es un punto de $C_1$ circunferencia, recorriendo al revés los pasos de la demostración anterior, que $Q$ está en la perpendicular a la línea del diámetro $OP’$ que pasa por el inverso de $P’$ $_\blacksquare$

Teorema (Inversión en Circunferencia ortogonal a C(O, r))

Sea $C(O,r)$ una circunferencia de inversión y sea $C_1$ una circunferencia ortogonal a $C$, el inverso de $C_1$ es $C_1$.

Demostración

Se traza una recta que pase por $O$ y $O_1$, la cual nos genere intersecciones en $C$ las cuales son $A$ y $B$, de igual forma en $C_1$ se genera $P$ y $P’$.

Inversión respecto a una circunferencia ortogonal a C(O,r).

Sea $C \perp C_1$ ortogonal, entonces $P$ y $P’$ son armónicos respecto a $A$ y $B$.

$\Leftrightarrow \frac{AP}{PB} = \frac{-AP’}{P’B} $

$\Leftrightarrow OP \times OP’ =r^2$

$\Leftrightarrow P$ y $P’$ son inversos respecto a $C$.

Tracemos una recta que pase por $O$ y corte a $C_1$ en $Q$ y $Q’ \in C_1$, y a $C$ en $A’$ y $B’ \in C$, tales que $Q$ y $Q’$ son armónicos respecto a $A’$ y $B’$

$\Leftrightarrow \frac{A’Q}{QB’} = \frac{-A’Q’}{Q’B’} $

$\Leftrightarrow OQ \times OQ’ =r^2$

$\Leftrightarrow P$ y $P’$ son inversos respecto a $C$.

Todo punto en una circunferencia ortogonal a la de inversión tiene su inverso en ella misma. Por lo tanto, $C_1$ es su propia inversa $_\blacksquare$

Tenemos observaciones que nos indica que los siguientes son sus propios inversos con respecto a la circunferencia de Inversión:

  • La propia circunferencia de Inversión
  • Rectas por el centro de Inversión
  • Circunferencias ortogonales a la circunferencia de Inversión

Teorema (Inversión en Circunferencia no Concéntrica con C(O, r))

El inverso de una circunferencia que no pasa por el centro de inversión, es otra circunferencia que tampoco pasa por el centro de Inversión.

Demostración

Tenemos $C_1$ una circunferencia con centro $A$, tomemos un punto $P$ sobre la circunferencia $C_1$, también tenemos $C(O,r)$ una circunferencia con centro de Inversión $O$.

Tracemos una recta $OP$, genera un punto de intersección $Q$, y se genera $P’$ inverso de $P$. Ahora tracemos la recta $OA$ y $QA$, además tracemos una paralela a $QA$ que interseque a $OA$ en $B$

Inversión respecto a una circunferencia no Concéntrica con C(O,r).

Por definición de Inversión $OP \times OP’=r^2$ y $OQ \times OP = w$, ahora como los triángulos $\triangle OBP’$ y $\triangle OAQ$ son semejantes, entonces

$\Leftrightarrow \frac{OP’}{OQ} = \frac{OB}{OA}=\frac{BP’}{AQ} $

$\Leftrightarrow \frac{OP’}{OQ} = \frac{OB}{OA} $

$\Leftrightarrow OB=\frac{OP’ \times OA}{OQ} $ como $OQ = w/OP$

$\Leftrightarrow OB=\frac{OP’ \times OA}{w/OP} =\frac{OP’ \times OP\times OA}{w}=\frac{r^2 \times OA}{w} $

Entonces $OB$ es constante, $B$ es un punto fijo y $BP’$ es finita y constante, entonces el lugar geometrico de $P’$ es una circunferencia $C’_1$, por lo cual el punto $P’$ no pasa por $O$.

Por lo tanto, el Inverso de $C_1$ es $C’_1$ $_\blacksquare$

Observación: Note que $P$ y $P’$ son puntos antihomologos, $Q$ y $P’$ son homólogos y $O$ es el centro de homotecia de las circunferencias $C_1$ con centro $A$ y $C’_1$ con centro $B$.

Teorema (Inversión en Circunferencia Concéntrica con C(O, r))

El inverso de una circunferencia concéntrica con la circunferencia de inversión, es otra circunferencia concéntrica con la circunferencia de inversión.

Demostración

Sea $C(O,r)$ nuestra circunferencia de Inversión y $C_1$ una circunferencia concéntrica a $C$

Circunferencia concéntrica con C(O,r).

Tomemos un punto en $C_1$ el cual es $P$, del cual su inverso es $P’$ con respecto a $C(O,r)$, entonces la distancia $OP$ es constante, al igual $r$ es constante y por definición de inversión $OP \times OP’ =r^2$ entonces $OP’=r^2/OP$ por lo cual $OP’$ es constante.

Por lo tanto, el inverso de $C_1$ es una circunferencia $C’_1$ con centro $O$ y radio $OP’$ $_\blacksquare$

Más adelante…

Otro aspecto a analizar de la inversión será la conservación de ángulos.

Entradas relacionadas

Geometría Moderna II: Unidad 2 Inversión

Por Armando Arzola Pérez

Deja un comentario

2.1 Puntos Inversos con respecto a una circunferencia

Introducción

Una vez visto la potencia de un punto P, es hora de analizar una nueva transformación «Inversión«.

Definición Inversión:

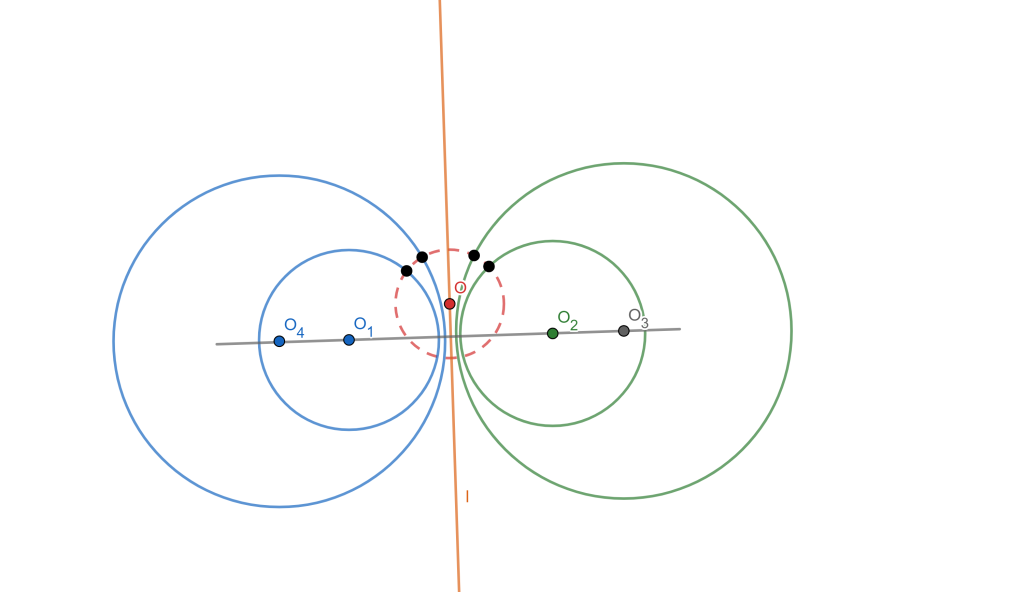
Sea una circunferencia $C(O,r)$ con centro $O$ y radio $r>0$. Si $P$ y $P’$ son dos puntos colineales con $O$ se tiene que $P’$ es el inverso de $P$ y viceversa si y solo si $P’O \times PO=r^2$.

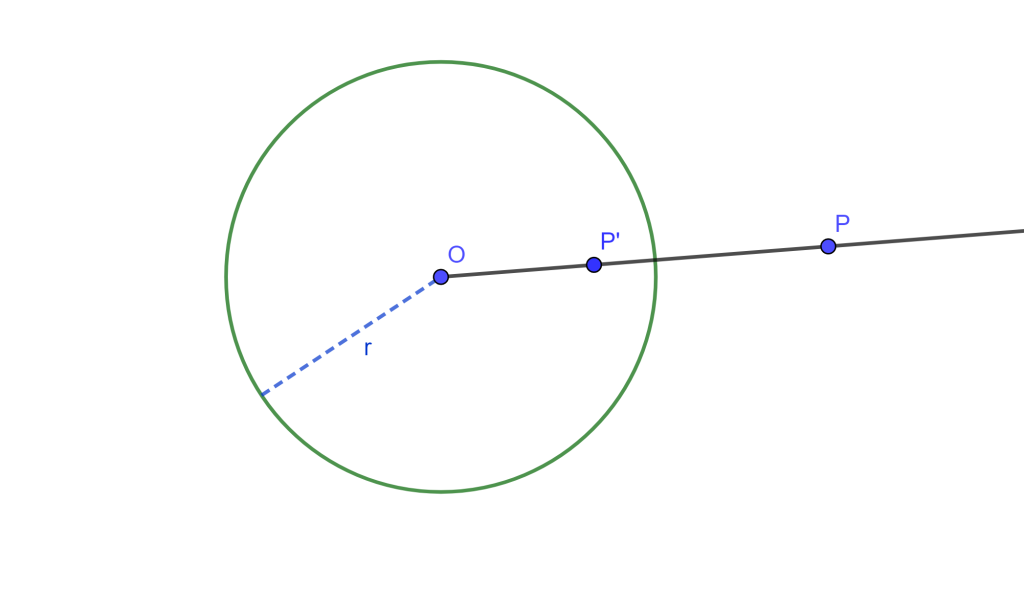
Definición de Inversión Gráfica

El punto $O$ es el centro de Inversión, la circunferencia $C$ es la circunferencia de inversión, y su radio $»r»$ es el radio de inversión.

Esta es una relación simétrica, ya que $P’$ es inverso de $P$ y $P$ es inverso de $P’$ con respecto a la circunferencia $C(O,r)$.

Propiedades de Inversión

  1. Cada punto en el plano, excepto el centro, tiene un inverso único.
  2. El inverso de un punto en la circunferencia de inversión es su propio inverso.
  3. El inverso de un punto interior a la circunferencia de inversión es siempre un punto exterior a la circunferencia de inversión.

De esta forma se puede construir el inverso de un punto $P$ con respecto a $C(O,r)$.

Proposición (Inversión)

Sea $C(O,r)$ una circunferencia y un punto $P$, por lo cual existe un $P’$ tal que $OP \times OP’ =r^2$.

Demostración

Se considera una circunferencia $C(O,r)$ y un punto $P$, pero existen 3 casos, el punto $P$ interno, externo y sobre la circunferencia $C(O,r)$.

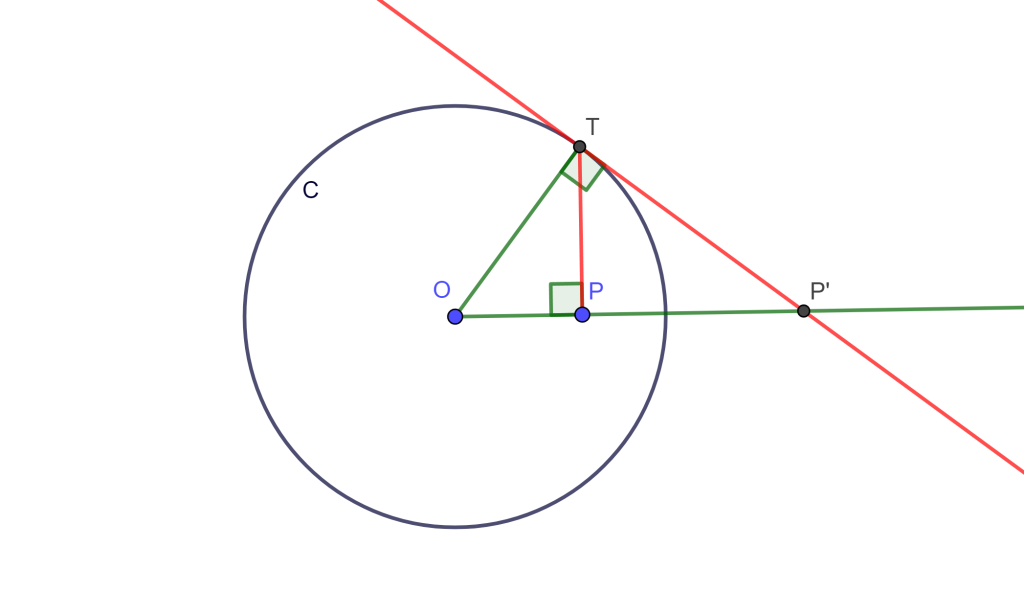
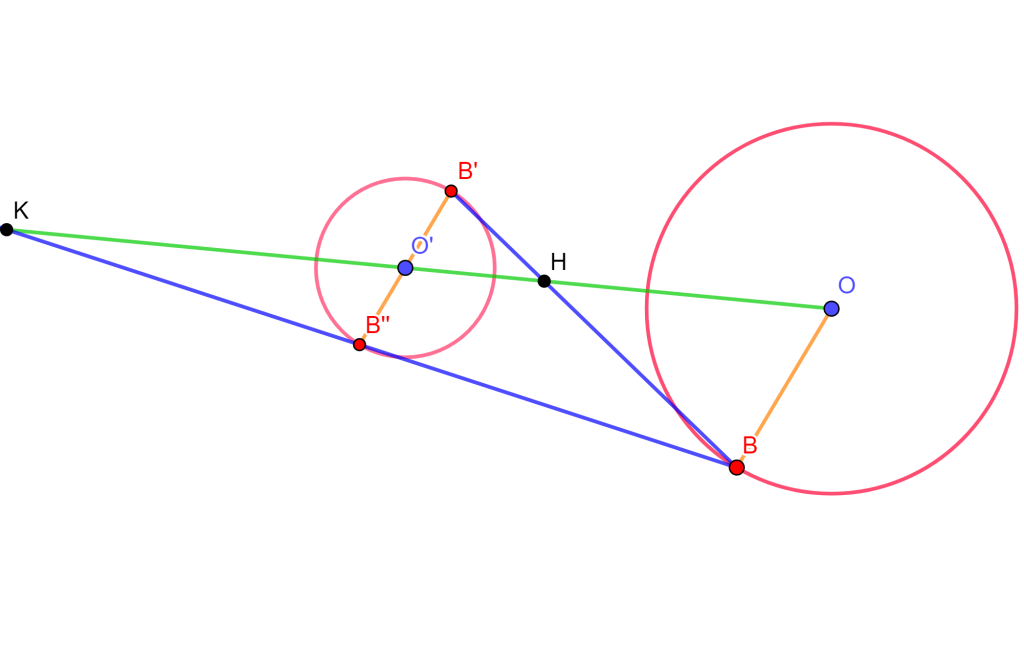
Caso 1: $P$ interno a $C(O,r)$

Trazamos la perpendicular a $OP$ por $P$, donde la intersección es $T$ de la perpendicular a $C(O,r)$. Trazamos $OT$ y trazamos la tangente a $C(O,r)$ por $T$, llamemos $P’$ a la intersección de $OP$ con respecto a la tangente mencionada.

Caso 1 Inversión

Por construcción $\angle OTP’ = \pi /2 = \angle OPT$, y los triangulos $\triangle OTP$ y $ \triangle OP’T$ comparten $\angle O$, por lo cual son semejantes, entonces $\triangle OTP \approx \triangle OP’T$.

$\Rightarrow \frac{OP’}{OT} = \frac{OT}{OP} \Leftrightarrow OP \times OP’ =r^2$ $_\blacksquare$

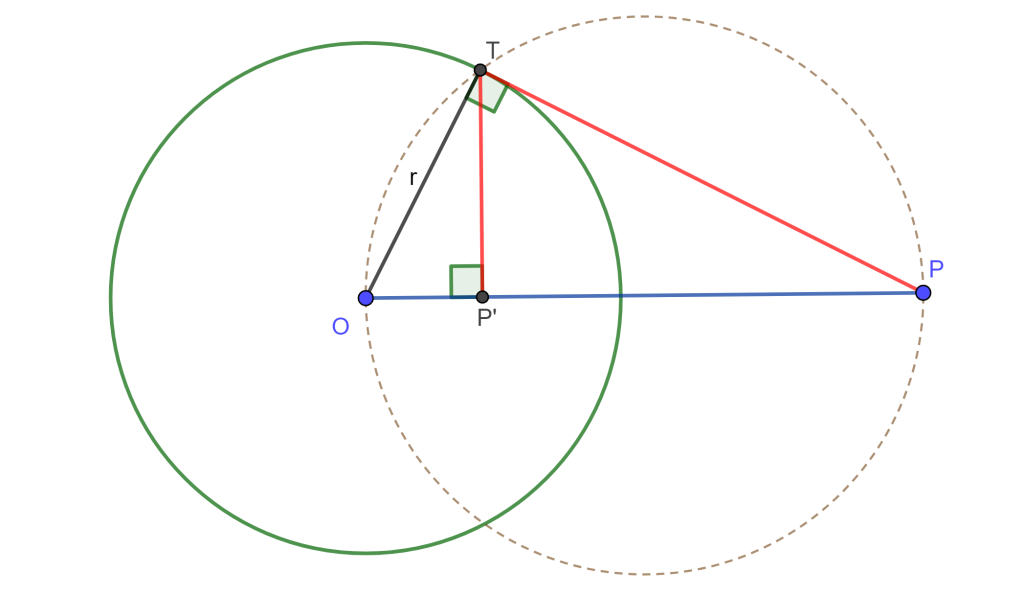
Caso 2: $P$ externo a $C(O,r)$

Trazamos una circunferencia de diámetro $PO$ y unimos $P$ con la intersección de las 2 circunferencias la cual llamaremos $T$.
De $T$ sacamos la perpendicular respecto a $OP$, la intersección será $P’$.

Cso 2 Inversión

El angulo $\angle OTP = \pi /2 $ ya que abarca el diametro $OP$. Ahora los $\triangle OP’T \approx \triangle OTP$ porque comparten $\angle TOP$ y $\angle OTP =\pi /2=\angle OP’T$

$\Rightarrow \frac{OP’}{OT} = \frac{OT}{OP} \Leftrightarrow OP’ \times OP=OT \times OT =r^2$ $_\blacksquare$

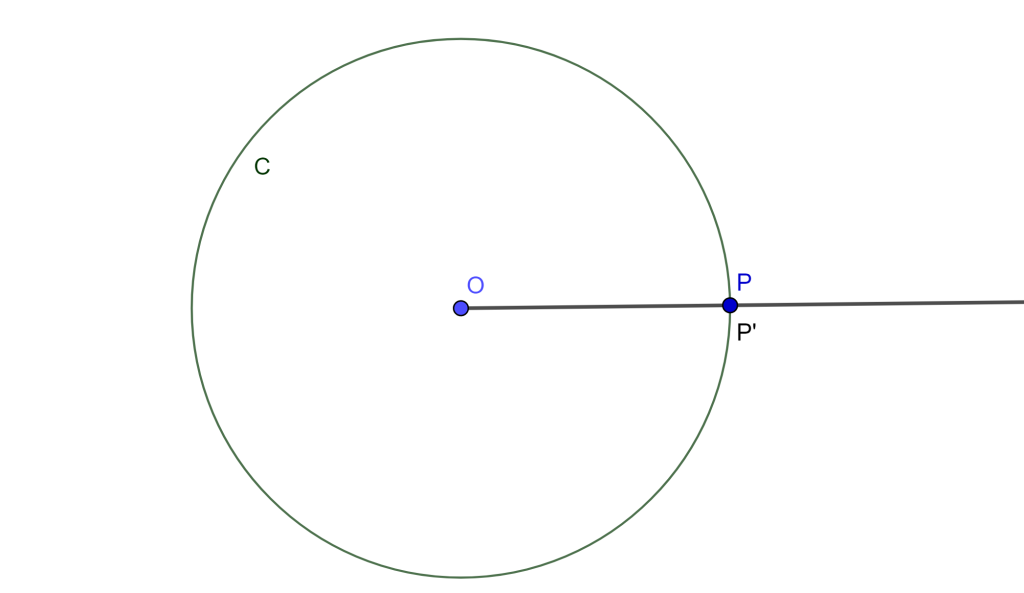
Caso 3: $P$ está en $C(O,r)$

Su inverso $P’$ con respecto a $C(O,r)$ es colineal con $P$ y $O$, y además $OP=r$ entonces se debe cumplir $OP \times OP’ =r^2$

Caso 3 Inversión


$\Rightarrow r \times OP’ =r^2 \Rightarrow OP’=r \Rightarrow OP’=OP \Rightarrow P’=P$ $_\blacksquare$

Ahora veremos un teorema que será útil más adelante.

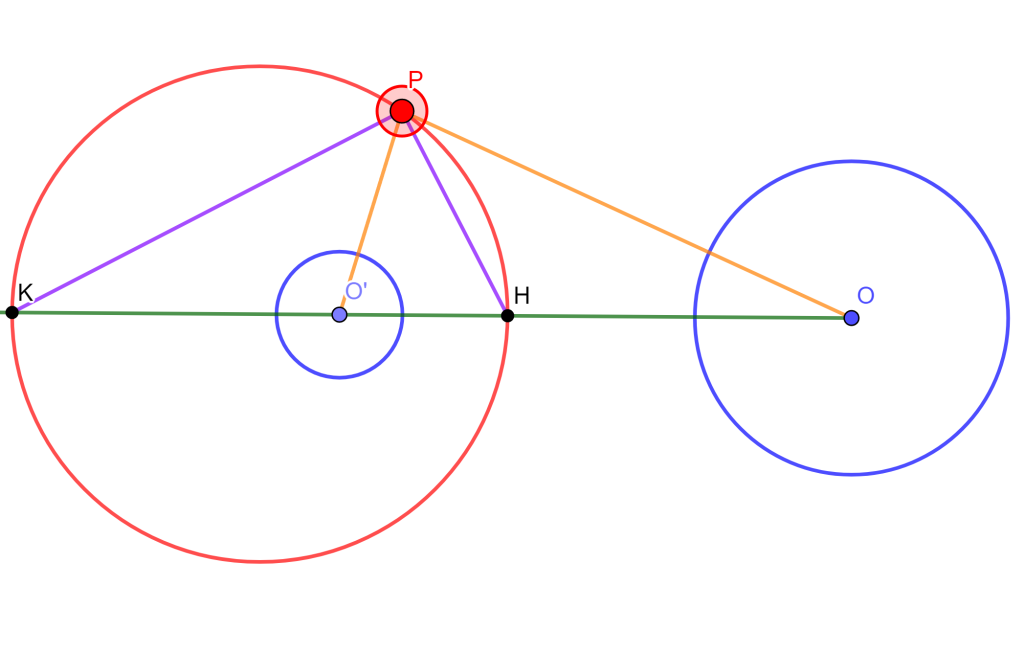
Teorema

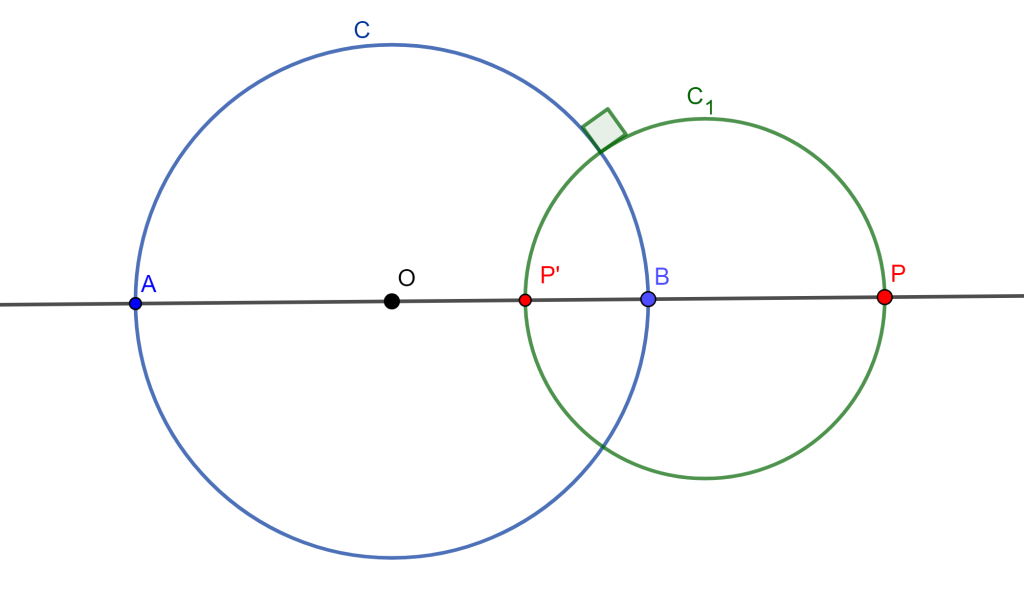
Sea $C(O,r)$ una circunferencia de inversión, $P$ y $P’$ dos puntos inversos respecto a $C$. Cualquier circunferencia que pase por $P$ y $P’$ es ortogonal a $C$.

Demostración

Sea $C$ una circunferencia y $OP$ un segmento, sean $A$ y $B$ los puntos donde $OP$ toca a $C$ y $B \in OP$

Ortogonalidad en circunferencias con puntos inversos

Por hipotesis $OP \times OP’ = r^2$ y $O$ es punto medio de $AB$
$\Rightarrow P’$ y $P$ son armonicos respecto a $A$ y $B$
$\Rightarrow (\frac{AP’}{P’B}) =-(\frac{AP}{PB})$
Ahora como $C$ pasa por $A$ y $B$, y $C_1$ pasa por $P’$ y $P$ entonces $C\perp C_1$ $_\blacksquare$

Más adelante

Una vez ya estudiado la definición de inversión y sus propiedades, es momento de analizar como afecta la inversión a otros objetos geométricos, en específico en Rectas y Circunferencias.

Entradas relacionadas

Geometría Moderna II: Ejercicios Unidad 1

Por Armando Arzola Pérez

Deja un comentario

Introducción

Una vez estudiado los temas de esta primera unidad, se dejarán a continuación Ejercicios para reforzar, investigar y pensar distintos problemas relacionados con lo ya visto en esta unidad.

Potencia de un Punto Ejercicios

1.- Dados dos círculos A y A’. Encontrar el lugar de los puntos cuya suma de Potencias respecto a A y A’ es constante.

2.- El lugar geométrico de un punto, cuya diferencia de potencias con respecto a dos circunferencias no concéntricas es constante, es una línea recta paralela a su eje radical.

Eje radical de dos circunferencias Ejercicios

3.- Construir el eje radical de dos circunferencias sin hacer uso de los centros o la línea de los centros de las circunferencias.

4.- Encontrar el eje radical del circuncirculo y el círculo de los nueve puntos de un triángulo dado.

Circunferencias Ortogonales Ejercicios

5.- Determinar cuando es posible para el centro de una de dos circunferencias ortogonales estar en la otra circunferencia.

6.- Dadas dos circunferencias y un punto, trace una circunferencia que sea ortogonal a las dos y que contenga al punto.

Familias Coaxiales Ejercicios

7.- Dos circunferencias distintas dadas, son miembro de uno y solo un conjunto de circunferencias coaxiales.

8.- Demuestra que si cada uno de dos puntos fijos tiene potencias iguales con respecto a tres o más circunferencias, estas son coaxiales.

9.- Demuestra que los ejes radicales de un círculo y cada una de las circunferencias de un conjunto coaxial son concurrentes.

10.- Demuestra que todas las circunferencias cuyos centros son colineales y tales que son ortogonales a una circunferencia dada, son coaxiales.

Circunferencia de Similitud Ejercicios

11.- Demuestre que dos circunferencias y su circunferencia de similitud son coaxiales.

Aplicaciones al Cuadrilátero Completo Ejercicios

12.- Demuestra que las circunferencias cuyos diámetros son las diagonales de un cuadrilátero completo son coaxiales.

Más Adelante…

Se abordará el tema de Inversión respecto a su teoría con distintos temas relacionados.

Entradas relacionadas

Geometría Moderna II: Aplicación al cuadrilátero completo

Por Armando Arzola Pérez

Deja un comentario

Introducción

Una vez analizado las circunferencias coaxiales es necesario ver la Aplicación al Cuadrilátero Completo.

Cuadriláteros completos

Recordemos que un cuadrilátero completo se define:

Definición. Un cuadrilátero completo es una figura que consiste de 4 líneas, tres de las cuales no pasan por el mismo punto y los seis puntos determinados por la intersección de estas líneas.

Cuadrilátero Completo Definición

Observaciones.

  • Las cuatro líneas son sus lados y los seis puntos son sus vértices. En este caso a, b, c y d son los lados y los puntos $a \cap c, b \cap c, c \cap d, d \cap b, a \cap d$ y $a \cap b$ son los vértices.
  • Se dice que dos vertices son vertices opuestos si ellos no estan en el mismo lado. En un cuadrilatero completo hay 3 pares de vertices opuestos. Son [$c \cap d $y$ a \cap b$], [$b \cap c$ y $a \cap d$] y [$a \cap c$ y $d \cap b$].
  • Las 3 líneas determinadas por los pares de vértices opuestos de un cuadrilátero completo, son sus diagonales, y el triángulo determinado por estas 3 líneas, es un triángulo diagonal. Las rectas son p, q y r son las rectas diagonales y pqr es el triángulo diagonal.

Una aplicación de la teoría de circunferencias coaxiales, es el siguiente teorema:

Teorema. Las circunferencias, cuyos diámetros son las diagonales de un cuadrilátero completo, son coaxiales.

Cuadrilátero Completo Aplicación Teorema 1

Demostración. Se tiene el cuadrilátero completo con lados p, q, r y s, donde se puede sacar el ortocentro $H_1$ del $\triangle ABC$ y $A’, B’ $y$ C’$ los pies de las alturas $A, B $y$ C$.

Puesto que $A, C, C’, A’$ y $ B, C, C’, B’$ son conjuntos de puntos conciclicos. Entonces $H_1A \cdot H_1A’=H_1B \cdot H_1B’=H_1C \cdot H_1C’$.

Ahora $AA’, BB’, CC’$ cuerdas de las circunferencias que tiene como diámetros a $AF, BE$ y $CD$ respectivamente. Y por las ecuaciones anteriores $H_1$ tiene la misma potencia respecto a cada una de estas circunferencias.

Y al saber que $H_1$ tiene las mismas potencias, entonces se concluye que las circunferencias son coaxiales. $\square$

Corolario. Los ortocentros de los cuatro triángulos determinados por los cuatro lados del cuadrilátero tomados tres a un tiempo son colineales.

Demostración. Por la demostración anterior, se puede demostrar que los ortocentros de los triángulos $ADE, BDF, CEF$ tiene cada uno iguales potencias con respecto a estas tres circunferencias. Por lo cual las tres circunferencias son coaxiales, los cuatro ortocentros están en el eje radical y los centros o puntos medios de las diagonales, están en una línea recta.

Además, la línea en la que están los cuatro ortocentros, es perpendicular a la línea que pasa por los puntos medios de las diagonales. $\square$

Más adelante…

Una vez visto y estudiado esta primera unidad se pondrán ejercicios para practicar en la siguiente entrada.

Entradas relacionadas

Geometría Moderna II: Circunferencia de similitud

Por Armando Arzola Pérez

Deja un comentario

Introducción

Definición. La circunferencia de similitud (o de homotecia) de dos circunferencias no concéntricas, es la circunferencia que tiene como diámetro el segmento que une sus centros de similitud (o de homotecia).

Definición.

Sean dos círculos no concéntricos. Se unirá el centro $O$ de uno de ellos a cualquier punto $B$ de su círculo, no colineal con los centros. Si dibujamos el diámetro del otro círculo paralelo a $OB$ entonces interseca la circunferencia en $B’$ y $B$.

Si hacemos que $BB’$ y $BB’$$’$ intersequen la línea de los centros de las circunferencias en $H$ y $K$, entonces $\triangle OBH \sim \triangle O’B’H$, y $\triangle OBK \sim \triangle O’B’$$’K$. De lo anterior los dos circulos son homoteticos y $H$ y $K$ los centros de Homotecia.

Circunferencia de Similitud, estudio del centro de similitud.

Teorema. La circunferencia de similitud de dos círculos no concéntricos es el lugar geométrico de los puntos, tales que la razón de las distancias entre sus centros es igual a la razón entre sus radios.

Demostración. Sean dos circunferencias dadas $\mathcal{C}_1(O,r)$ y $\mathcal{C}_2(O’,r’)$, donde existen $H$ y $K$ sus centros de Homotecia.

Teorema Circunferencia de Similitud

$\boldsymbol{\Rightarrow} ]$

Sea un punto $P$ talque $PO:PO’ =r:r’$, esto se ve como $\frac{PO}{PO’}=\frac{r}{r’}$. Queremos demostrar que $P$ es un punto del lugar geométrico.

Entonces como $KO:KO’=OH:HO’=r:r’$, se sigue que $K$ y $H$ son puntos del lugar geometríco. Ahora como $PO’:PO=r’:r$ entonces $PO’:PO=KO’:KO=O’H:HO.$

Por el Teorema de la Bisectriz interna y externa $PH$ y $PK$ son las bisectrices interior y externa del angulo $\angle O’PO$. Entonces $PH$ y $PK$ son perpendiculares, y $P$ está en el círculo de similitud. $\square$

$\boldsymbol{\Leftarrow} ]$

Supongamos que $P$ está en el círculo de similitud. En la línea de los centros tenemos $O’$$’$ tal que $PH$ bisecta el angulo $O’PO’$$’$.

Entonces, ya que $PH$ y $PK$ son perpendiculares y que bisecan los ángulos interior y exterior en $P$ del triángulo $\triangle O’$$’PO’$, entonces

$O’$$’H:HO’=-O’$$’K:KO’$

además

$OH:HO’=-OK:KO’$

Entonces

$HO’$$’:O’$$’K=HO:OK$

Entonces $O’$$’$ coincide con $O$. Se tiene que $PO:PO’=r:r’$ $\square$

Del teorema anterior es necesario que $r \neq r’$, ya que si $r=r’$ syss $r/r’ =1$. Si dos círculos son iguales, su círculo de similitud degenera en la mediatriz del segmento que une sus centros y la línea al infinito.

Observación. la generalización del concepto de circunferencia de similitud es la circunferencia de Apolonio.

Teorema. El lugar geométrico de los puntos, cuyas razones de sus distancias a dos puntos fijos es una constante, es la circunferencia de Apolonio.

Sean los puntos fijos $O$ y $O’$ la razón de sus distancias a $P$ desde $O$ y $O’$, sea $r:r’$. Construiremos círculos con centros en $O$ y $O’$ cuyos radios tengan la razón $r:r’$. Por la demostración anterior, el lugar geométrico de los puntos $P$ es el círculo de similitud.

Más adelante…

Ya analizadas las circunferencias coaxiales, se verán aplicaciones al cuadrilátero completo.

Entradas relacionadas