Introducción
Una vez analizado las circunferencias coaxiales es necesario ver la Aplicación al Cuadrilátero Completo.
Cuadriláteros completos
Recordemos que un cuadrilátero completo se define:
Definición. Un cuadrilátero completo es una figura que consiste de 4 líneas, tres de las cuales no pasan por el mismo punto y los seis puntos determinados por la intersección de estas líneas.
Observaciones.
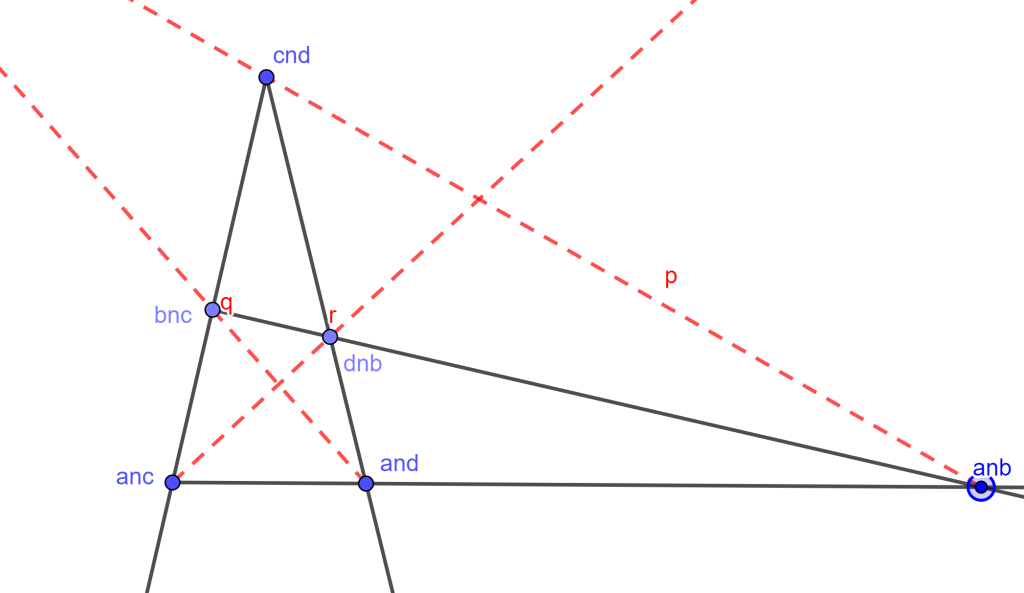
- Las cuatro líneas son sus lados y los seis puntos son sus vértices. En este caso a, b, c y d son los lados y los puntos $a \cap c, b \cap c, c \cap d, d \cap b, a \cap d$ y $a \cap b$ son los vértices.
- Se dice que dos vertices son vertices opuestos si ellos no estan en el mismo lado. En un cuadrilatero completo hay 3 pares de vertices opuestos. Son [$c \cap d $y$ a \cap b$], [$b \cap c$ y $a \cap d$] y [$a \cap c$ y $d \cap b$].
- Las 3 líneas determinadas por los pares de vértices opuestos de un cuadrilátero completo, son sus diagonales, y el triángulo determinado por estas 3 líneas, es un triángulo diagonal. Las rectas son p, q y r son las rectas diagonales y pqr es el triángulo diagonal.
Una aplicación de la teoría de circunferencias coaxiales, es el siguiente teorema:
Teorema. Las circunferencias, cuyos diámetros son las diagonales de un cuadrilátero completo, son coaxiales.
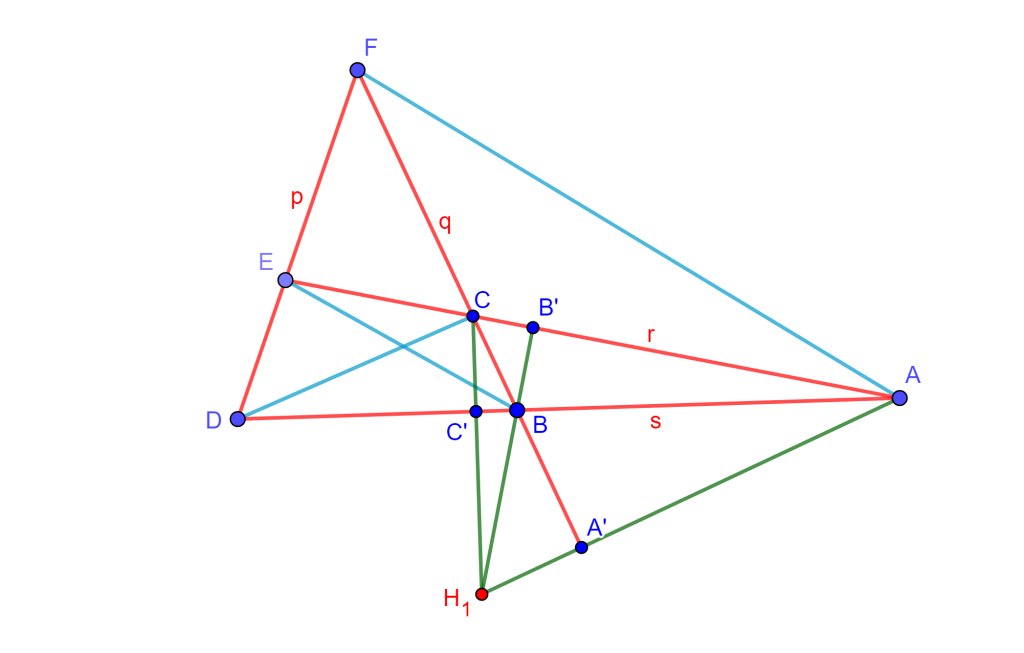
Demostración. Se tiene el cuadrilátero completo con lados p, q, r y s, donde se puede sacar el ortocentro $H_1$ del $\triangle ABC$ y $A’, B’ $y$ C’$ los pies de las alturas $A, B $y$ C$.
Puesto que $A, C, C’, A’$ y $ B, C, C’, B’$ son conjuntos de puntos conciclicos. Entonces $H_1A \cdot H_1A’=H_1B \cdot H_1B’=H_1C \cdot H_1C’$.
Ahora $AA’, BB’, CC’$ cuerdas de las circunferencias que tiene como diámetros a $AF, BE$ y $CD$ respectivamente. Y por las ecuaciones anteriores $H_1$ tiene la misma potencia respecto a cada una de estas circunferencias.
Y al saber que $H_1$ tiene las mismas potencias, entonces se concluye que las circunferencias son coaxiales. $\square$
Corolario. Los ortocentros de los cuatro triángulos determinados por los cuatro lados del cuadrilátero tomados tres a un tiempo son colineales.
Demostración. Por la demostración anterior, se puede demostrar que los ortocentros de los triángulos $ADE, BDF, CEF$ tiene cada uno iguales potencias con respecto a estas tres circunferencias. Por lo cual las tres circunferencias son coaxiales, los cuatro ortocentros están en el eje radical y los centros o puntos medios de las diagonales, están en una línea recta.
Además, la línea en la que están los cuatro ortocentros, es perpendicular a la línea que pasa por los puntos medios de las diagonales. $\square$
Más adelante…
Una vez visto y estudiado esta primera unidad se pondrán ejercicios para practicar en la siguiente entrada.
Entradas relacionadas
- Ir a Geometría Moderna II
- Entrada anterior del curso: Circunferencia de similitud
- Siguiente entrada del curso: Ejercicios de la Unidad 1