Introducción

Hemos hablado ya de relaciones entre conjuntos, sobre imagen, dominio y composición. Ahora vamos a ver algunas relaciones especiales entre conjuntos, que son la inyectividad, la suprayectividad y relaciones de un conjunto en sí mismo.

Inyectividad de una relación

Las ideas de los dos tipos de relación que vamos a exponer son inyectividad y suprayactividad. La inyectividad es una idea que nos va a hablar de cómo podemos relacionar un elemento de la imagen de una relación con un elemento del dominio. En pocas palabras lo que nos dirá la inyectividad es: Una relación inyectiva es aquella en la que los distintos elementos del dominio van a elementos de la imagen distintos. Veamos esto con calma con un ejemplo.

Supongamos que a nosotros nos interesa recuperar los elementos del dominio con los de la imagen, es decir, quisiéramos ver para cada pareja $y$ de la imagen, de qué $x$ proviene. En el caso de que haya dos relaciones distintas $(x,y),(z,y)$ nos causaría conflicto, pues podríamos decir que $y$ «viene» de dos distintos elementos del dominio.

Una relación inyectiva es aquella en donde para cada elemento de la imagen, existe un único elemento del dominio que se relaciona con esta. Es decir, una relación inyectiva $R$ será aquella en donde para cada $y\in Im(R)$, solo existe un elemento $x\in Dom(R)$ tal que $(x,y)\in R$. Otra forma de verlo es con la siguiente definición:

Definición. Sean $X,Y$ dos conjuntos y $R$ una relación de $X$ en $Y$. Diremos que $R$ es inyectiva si $$\mathrm{\forall }y\in Im(R)(\mathrm{\exists }!x\in X:(x,y)\in R)$$

Observa ahora que esto significa que si $R$ es una relación inyectiva y dos parejas $(x,y),(z,y)$ pertenecen a la relación $R$, entonces no les queda de otra que ser la misma pareja, esto implica que $x=z$.

Proposición. Sea $R$ una relación entre dos conjuntos $X$ y $Y$. Entonces son equivalentes:

1. $R$ es una relación inyectiva.
2. Si $(x,y)\in R$ y $(w,y)\in R$ entonces $x=w$.

Demostración.

$1)\Rightarrow 2)$. Consideremos $(x,y)\in R$ y $(w,y)\in R$. Lo que queremos demostrar es que $x=w$, para ello notemos que $R$ es inyectiva, lo que quiere decir que existe una única pareja $(x,y)\in R$. Esto quiere decir que $(x,y)=(w,y)$ y esto solo sucede si $y=y$ y $x=w$. Siendo la segunda igualdad la buscada.

$2)\Rightarrow 1)$. Ahora supongamos que si $(x^{\prime },y^{\prime })\in R$ y $(w^{\prime },y^{\prime })\in R$ entonces $x^{\prime }=w^{\prime }$. Y supongamos que $y$ es un elemento de la imagen de $R$. Demostremos ahora que existe un único elemento $x$ tal que $(x,y)\in R$. Para ello mostraremos que existe al menos un elemento $x$ tal que $(x,y)$ y cualquier otro elemento $w$ no cumple tal propiedad. Para demostrar lo primero, notemos que $y$ es un elemento del contradominio, lo que quiere decir que existe al menos un elemento $x\in X$ tal que $(x,y)\in R$. Y finalmente para demostrar que $x$ es único, supongamos existe un elemento $w\in X$ distinto a $x$ tal que $(w,y)\in R$. Pero por hipótesis, si pasa esto entonces $x=w$, lo cual es una contradicción pues hemos dicho que $x$ es distinto a $w$. De esta manera, $x$ sí es único.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

También es análogo pensar que si una relación $R$ es inyectiva, entonces para cada elemento de la imagen $y$, sucede que $I{m}^{-1}[\{y\}]$ tiene un único elemento, pues la definición nos dice que solo existe un elemento $x$ del dominio que se relaciona con $y$.

Ahora observa por ejemplo a los conjuntos de animales $X$ y el tipo de animales $Y$. Podríamos decir que en tipos de animales, tenemos aquellos que viven en la tierra (terrestres) y los que viven en el agua (acuáticos). Entonces una parte de la relación $R$ que relaciona el animal con el hábitat que tiene, se vería de la siguiente manera:

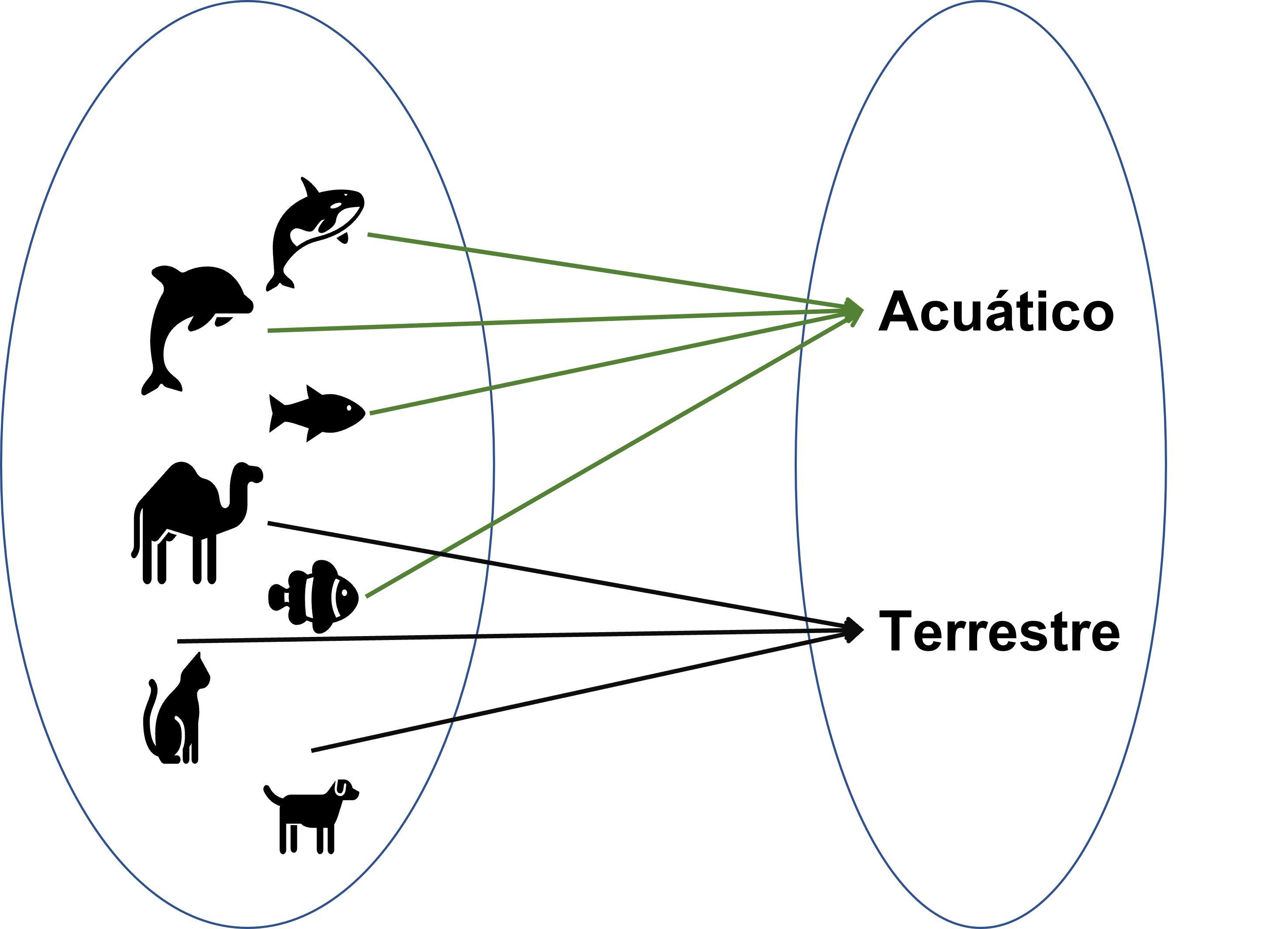
Ahora, si nos preguntamos, cuáles son los animales terrestres, deberíamos observar que al menos los animales terrestres son los perros, gatos, camellos, etc. Una relación que no es inyectiva, no nos regresa un único elemento, sino que un subconjunto del dominio de más de un elemento. Así que esta relación no es inyectiva.

Por otro lado, una relación que sí es inyectiva entre los conjuntos $X=\{a,b,c,d,e,f\}$ y $\mathbb{Z}$ es la relación $R$:

$$R=\{(a,y):y\in Z\}$$

Es inyectiva pues los elementos de esta relación se ven como: $R=\{\dots ,(a,-1),(a,0),(a,1),(a,2),\dots \}$ Y si agarramos cualquier número en la imagen de la relación, solo vendrá de un elemento, el elemento $a$.

Otros ejemplos de relaciones inyectivas son:

$R=\{(x,y)\in {\mathbb{Z}}^2:x=y\}$
$R=\{(x,y)\in {\mathbb{Z}}^2:x=2y\}$
$R=\{(x,y)\in {\mathbb{Z}}^2:(0,y)\text{ si }y\text{ es par,}(1,y)\text{ en otro caso}\}$

Relaciones suprayectivas

Otro concepto que será interesante es el de la suprayactividad. Este en términos simples nos dice que una relación $R$ es suprayectiva entre dos conjuntos $X,Y$ si cada elemento de $Y$ se relaciona con algún elemento de $X$. Es así como la siguiente definición nos lo menciona:

Definción. Sean $X,Y$ dos conjuntos y $R$ una relación de $X$ en $Y$. Diremos que $R$ es suprayectiva si $Im[Y]=Y$.

Una forma alterna de verlo es como en la siguiente proposición nos lo demuestra, siendo que siempre podremos encontrar una pareja para cada elemento $y$ de $Y$:

Proposición. Una relación $R$ es suprayectiva si y solo si $\mathrm{\forall }y\in Y(\mathrm{\exists }x\in X:(x,y)\in Y)$

Demostración Sean $X,Y$ dos conjuntos y $R$ una relación de $X$ en $Y$

$\Rightarrow$] Por hipótesis, $R$ es suprayectiva. Para demostrar que $\mathrm{\forall }y\in Y(\mathrm{\exists }x\in X:(x,y)\in Y)$ consideraremos un elemento $y\in Y$ arbitrario y demostraremos que existe algún elemento $x\in X$ tal que $(x,y)$ sea un elemento de la relación.
Como hipótesis, sabemos que la imagen de $R$ es igual a $Y$, esto quiere decir que:$$Y=Im(R)=\{y\in Y:\mathrm{\exists }x\in X\text{ tal que }(x,y)\in R\}.$$ De esta manera, $$y\in \{y\in Y:\mathrm{\exists }x\in X\text{ tal que }(x,y)\in R\}.$$ De manera que $\mathrm{\exists }x\in X\text{ tal que }(x,y)\in R$. Por lo tanto, $\mathrm{\forall }y\in Y(\mathrm{\exists }x\in X:(x,y)\in Y)$

$\Leftarrow$]. Ahora supongamos por hipótesis que para cada elemento $y\in Y$, existe un elemento $x\in X$ tal que $(x,y)\in R$. Ahora, demostremos que $R$ es suprayectiva, es decir $Im(R)=Y$. Para esto, tendremos que demostrar que $Y$ está contenido en $Im(R)$ y viceversa. Pero nota que $Im(R)$ siempre es un subconjunto de $Y$ (pues por definición, sus elementos son elementos de $Y$). Así que bastará demostrar que $Y\subset Im[R]$. Para ello, considera un elemento $y\in Y$. Por hipótesis, para aquel elemento, existirá $x\in X$ tal que $(x,y)\in R$. Pero esto significa que $y\in Im[Y]$. Así, $Y\subset Im[R]$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Un ejemplo de una función suprayectiva sobre los conjuntos $X=\{1,2,3\},Y=\{0\}$ es la relación $R=\{(1,0),(3,0)\}$. Esto puesto que hay solo un elemento en el conjunto $Y$ y hay al menos una relación para cada elemento del conjunto $Y$. Esto quiere decir que «cubrimos» a todo el contradominio. Otros ejemplos de funciones suprayectivas son:
$R=\{(x,y)\in {\mathbb{Z}}^2:x=y\}$
$R=\{(x,y)\in \mathbb{Z}\times \{0,1,2,3,4\}:x=1\wedge y\in \{0,1,2,3,4\}\}$
Si $R$ es una relación entre dos conjuntos, $X,Y$, la relación $R=X\times Y$ es suprayectiva.

Relaciones de un conjunto en sí mismo

Hemos estado hablando ya de un conjunto muy particular, ${\mathbb{Z}}^2$ que lo definimos como $\mathbb{Z}\times \mathbb{Z}$, es decir de relaciones en el conjunto de los números enteros en sí mismo. Este tipo de relaciones, como ya lo hemos mencionado, se les acostumbra a poner un subíndice ${}^2$ para indicar que estamos hablando del producto cartesiano de un conjunto sobre él mismo. Por ejemplo si $X$ es un conjunto, entonces $X^2=X\times X$. Vamos a concentrarnos ahora en algunas relaciones especiales de un conjunto en sí mismo.

La primera relación que veremos será la reflexividad, y esto se da cuando un elemento está relacionado consigo mismo. Por ejemplo, en ${\mathbb{Z}}^2$, la relación cuyos elementos son de la forma $(x,x)$ siempre será reflexiva, pues cada elemento $x$ está relacionado consigo mismo.

La segunda relación se llama la simetría, que nos indica que para cada pareja $(x,y)$ de la relación, sucederá que igual $(y,x)$ estará en la relación. Si te das cuenta, algo que nos dice esta relación es que el orden «no importa», pues da igual cuál elemento escribamos del lado izquierdo y del lado derecho, pues su homónimo simétrico estará igual en la relación.

La tercera es un concepto similar al segundo pero en su antónimo. Diremos que una relación es antisimétrica si para cada pareja que tengamos en la relación $(x,y)\in R$, no sucederá que $(y,x)\in R$ a menos que $x=y$. Piensa por ejemplo para esto, en la relación «ser menor o igual a un número» $\le$. Sucede que $1\le 2$ pero no que $2\le 1$.

Finalmente, la cuarta propiedad es llamada la transitividad. Esto lo que nos indica es que la composición de la relación también es parte de la relación. En otras palabras, si $(x,y),(y,z)\in R$ entonces $(x,z)\in R$. Para pensar en un ejemplo, piensa en la igualdad entre números, si $1+1=2$ y $2=4-2$, entonces $1+1=4-2$.

Anotaremos este tipo de relaciones como una definición

Definición. Sea $R$ una relación de un conjunto $X$ en sí mismo. Diremos que:

• $R$ es reflexiva si $\mathrm{\forall }x\in X,(x,x)\in R$
• $R$ es simétrica si $\mathrm{\forall }x\in X\mathrm{\forall }y\in X((x,y)\in R\Rightarrow (y,x)\in R)$
• $R$ es antisimétrica si $\mathrm{\forall }x\in X\mathrm{\forall }y\in X(((x,y)\in R\wedge (y,x)\in R)\Rightarrow (x=y))$
• $R$ es transitiva si $\mathrm{\forall }x\in X\mathrm{\forall }y\in X\mathrm{\forall }z\in Z(((x,y)\in R\wedge (y,z)\in R)\Rightarrow (x,z)\in R)$

Más adelante…

En la siguiente entrada entraremos a los ordenes parciales, los cuales son relaciones de un conjunto sobre sí mismo que cumplen algunas de las clases especiales de relaciones que hemos revisado en esta entrada. De hecho quizá ya tengas una idea intuitiva de qué es un orden, concepto que ampliaremos más en lo que sigue.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Sean $X,Y$ dos conjuntos y $R$ una relación de $X$ en $Y$.Demuestra que son equivalentes:
   1. $R$ es inyectiva
   2. $\mathrm{\forall }y\mathrm{\forall }x(((x,y)\in R\wedge (z,y)\in R)\Rightarrow x=z)$
   3. $\mathrm{\forall }y\in Im(R)(I{m}^{-1}[\{y\}]\text{ tiene un solo elemento})$
2. Demuestra que las siguientes relaciones son inyectivas:
   • $R=\{(x,y)\in {\mathbb{Z}}^2:x=y\}$
   • $R=\{(x,y)\in {\mathbb{Z}}^2:x=2y\}$
   • $R=\{(x,y)\in {\mathbb{Z}}^2:(0,y)\text{ si }y\text{ es par,}(1,y)\text{ en otro caso}\}$
3. Sea la relación $R$ sobre el conjunto $X$ de los seres humanos dada por: $$R=\{(x,y)\in X^2:x\text{ tiene el mismo cumpleaños que }y\}.$$ Demuestra que $R$ es una relación reflexiva, simétrica y transitiva.

Entradas relacionadas

• Ir a Álgebra Superior I
• Entrada anterior del curso: Relaciones en conjuntos: dominio, codominio y composición
• Siguiente entrada del curso: Problemas de relaciones y tipos de relaciones

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»