Introducción
Esta entrada es parte de una serie de notas introductorias sobre técnicas de demostración. En esta entrada se habla sobre demostraciones directas e indirectas. Cada entrada está ligeramente relacionada con las otras. Para entenderlas bien, usamos el siguiente diagrama que recopila cómo se comporta un mundo fantástico llamado Axios, en donde habitan creaturas llamadas Blorgs. Para leer más sobre ello, haz click aquí.
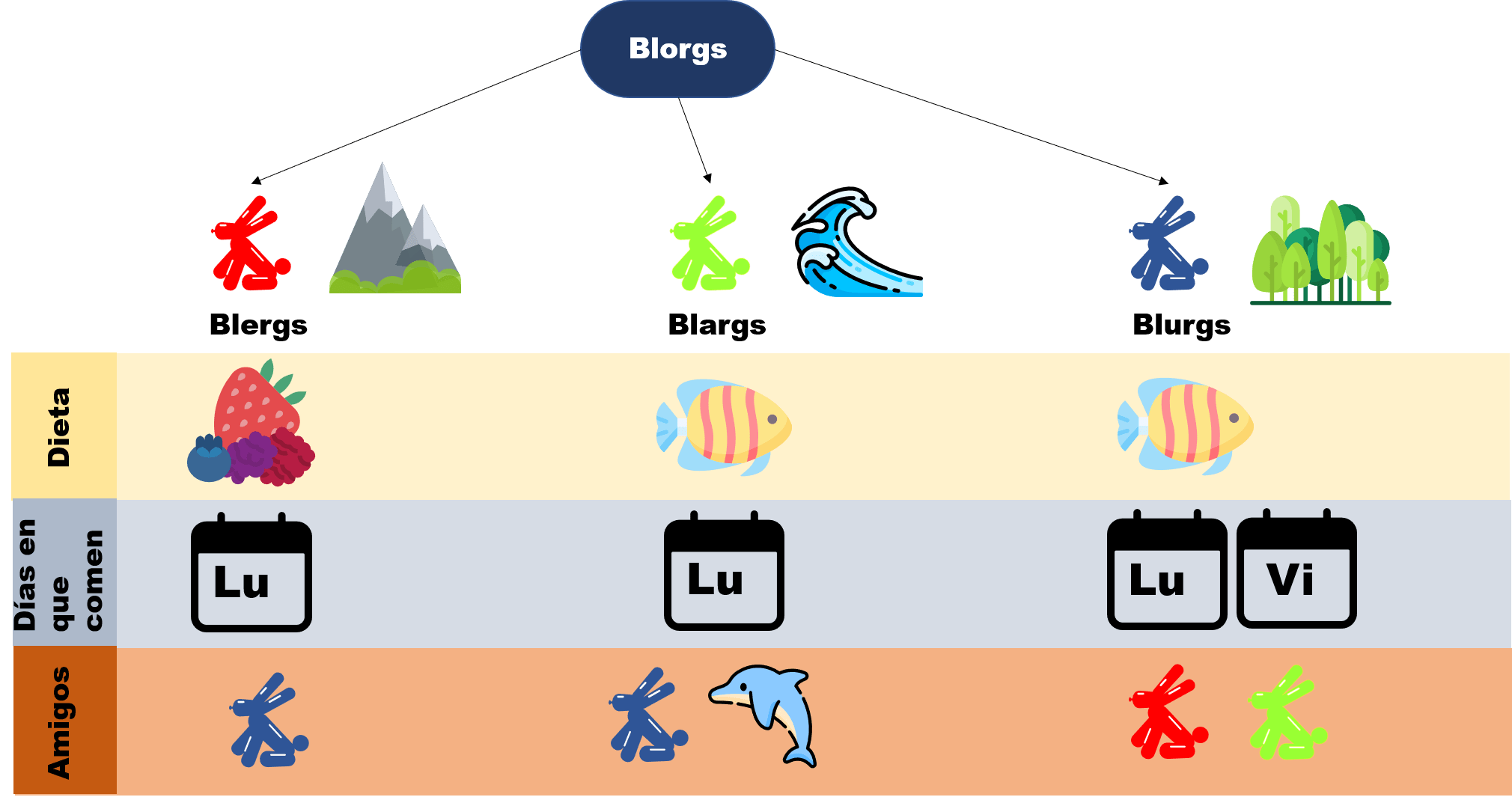
Hasta ahora hemos introducido algunos conceptos introductorios de lo que es una demostración matemática, pero apenas estamos por iniciar este recorrido hacia lo que son estas. Ahora, empezaremos por ver dos formas de pensar al demostrar que son las demostraciones directas e indirectas.
Demostraciones directas
Ahora vamos a explorar un poco más esto de las demostraciones, qué son y cómo nos ayudan. ¿Recuerdas nuestro ejemplo de que todos los Blorgs verdes comían peces? Este es un ejemplo de lo que llamamos demostraciones directas. Este nombre viene del hecho de que partimos de una lista de proposiciones válidas y vamos obteniendo más proposiciones válidas a través de reglas de inferencia básicas hasta que tenemos la conclusión deseada. En general este tipo de demostraciones van a ser cadenas de implicaciones. Por ejemplo partiendo de
$P_0 \Rightarrow P_1, P_1\Rightarrow P_2, P_2 \Rightarrow P_3, \dots, P_{n-1} \Rightarrow P_{n} $
concluiremos que $P_0 \Rightarrow P_{n}$. Esto en términos sencillos quiere decir: las demostraciones directas van a ser aquellas que podemos dar «el paso claro». Retomando nuestra analogía con las piezas Leog, si sabemos que con madera podemos construir las patas y el asiento, y con patas y el asiento podemos construir una silla, entonces ya sabríamos que con madera podemos construir una silla, pues decimos: «Primero con la madera construimos las patas y el asiento, y después con las patas y el asiento construimos la silla». Cuando veamos otros tipos de demostraciones, verás más fácilmente porqué tienen este nombre. Mientras tanto veamos otro ejemplo.
Proposición. Si un Blorg vive en las montañas, entonces come los lunes.
Demostración. Recordemos cómo empezamos la demostración de la entrada pasada, empezamos con un Blorg que vive en las montañas y veremos poco a poco que come los lunes. Para empezar, nota que con las siguientes proposiciones:
$P(x) = x \text{ vive en las montañas} $
$Q(x) = x \text{ es un Blerg},$
tenemos como axioma (y por lo tanto como cierto) que
$$P(x) \Rightarrow Q(x).$$
Además, sabemos que todos los Blergs comen los lunes, es decir, suponiendo que $R(x) = x \text{ come los lunes}$ entonces es cierto que
$$Q(x) \Rightarrow R(x).$$
Y la siguiente regla de inferencia es válida:
\begin{array}{rl}
& P \Rightarrow Q \\
& Q \Rightarrow R \\
\hline
\therefore & P \Rightarrow R.
\end{array}
Entonces podemos aplicar esta regla de inferencia a nuestro problema, dando como resultado que
$$P(x) \Rightarrow R(x).$$
Ahora recuerda que en las demostraciones nuestro objetivo va a ser «generalizar». No basta con que un Blorg en las montañas coma los lunes, si no quisieramos que siempre que veamos a un Blorg en las montañas, sepamos que come los lunes.
Para esto, empezaremos con un Blorg a quien le llamaremos $x$ y lo único que sabemos de este Blorg es que vive en las montañas, es decir $P(x)$. Ahora, aplicando las reglas de inferencia, sabemos que si $P(x)$ entonces también $R(x)$. Esto quiere decir que sabiendo que un Blorg vive en las montañas, ya sabemos que también come los lunes. Recuerda que para hacer este paso aplicamos las reglas de inferencia. De esta manera, $x$ come los lunes.
Por lo tanto, los Blorgs que viven en las montañas comen los lunes.
$\square$
Demostraciones indirectas
Otra estrategia para demostrar cosas va a ser mediante lo que se conoce como demostraciones indirectas. Esta forma de demostrar proposiciones va a usar la siguiente regla de inferencia:
\begin{array}{rl}
& P \Rightarrow Q \\
\hline
\therefore &(\neg Q) \Rightarrow (\neg P).
\end{array}
¿Recuerdas que la premisa es equivalente a la conclusión? Pues el que sea equivalente es suficiente para que sea una regla de inferencia válida. Puedes verificarlo haciendo la tabla de verdad.
¿Por qué usaremos esta regla de inferencia? Porque a veces queremos mostrar $P\Rightarrow Q$, pero es mucho más «tangible» mostrar la contrapositiva $\neg Q\Rightarrow \neg P$ pues a veces $\neg Q$ nos da más sustancia matemática con la cual trabajar. Por ejemplo, quizás $Q$ tiene un cuantificador universal, y al negarlo se convierte en un cuantificador existencial, que nos permite tomar a un objeto matemático que no tenga cierta propiedad y de ahí mostrar $P$.
Veamos un ejemplo en donde puede aplicarse una demostración indirecta.
Proposición. Si un Blorg come peces, entonces tiene dos tipos de amigos.
Demostración. Aquí podríamos intentar proceder directamente. Tomar un Blorg que coma peces. Pero esto nos lleva a un pequeño problema: al hacer esto la demostración se divide en dos casos: que el Blorg sea Blarg, o que sea Blurg. Podríamos hacer cada caso, y platicaremos de eso más adelante. Pero pensemos en por qué una demostración indirecta nos ayudaría a argumentar más fácilmente. Tomemos las siguientes proposiciones:
$P(x) = x \text{ es come peces}$
$Q(x) = x \text{ tiene dos tipos de amigos}.$
Queremos mostrar que $P(x)\Rightarrow Q(x)$. Pero lo que nos dice la regla de inferencia de arriba es que esto es lo mismo que demostrar que $\neg Q \Rightarrow \neg P$. Ahora notemos que
$\neg Q(x) = x \text{ no tiene dos tipos de amigos} = x \text{ tiene un tipo de amigos}$
$\neg P(x) = x \text{ no come peces} = x\text{ come frutos rojos}.$
Podemos argumentar entonces como sigue. Tomemos $x$ un Blorg que tiene un tipo de amigos. Por ello, $x$ es un Blerg. Además sabemos que «si $x$ es Blerg, entonces come frutos rojos». Por lo tanto, $x$ come frutos rojos.
Hemos mostrado entonces la contrapositiva «Si $x$ tiene un tipo de amigos, entonces $x$ come frutos rojos». Por la equivalencia entre una implicación y su contrapositiva, hemos demostrado que «Si $x$ come peces, entonces tiene dos tipos de amigos.»
$\square$
Algunas notas sobre las demostraciones anteriores
Vamos a hacer algunas observaciones sobre la forma en que demostramos nuestras proposiciones.
- En la primera demostración usamos nuevamente una cadena de implicaciones, como en la entrada anterior. Observa que aunque estamos demostrando cosas distintas, en el fondo estamos usando exactamente el mismo tipo de inferencias matemáticas.
- En la segunda demostración podíamos, alternativamente, intentar proceder directamente. Si un Blorg come peces, entonces puede ser Blarg o Blurg. Pero este «o» nos lleva a dos posibilidades. Tenemos que cubrir ambas posibilidades mediante una demostración por casos, de la cual hablaremos más adelante. La manera indirecta de proceder nos permitió evitar los casos.
Más adelante…
Hasta ahora tenemos dos formas de demostrar: demostraciones directas e indirectas. En pocas palabras las directas usan sucesiones de proposiciones que ya sabemos para llegar a una conclusión, mientras que las indirectas no empiezan por lo que quiere demostrar, sino que muestran que si la conclusión no es cierta, entonces la premisa no lo es.
Continuando con nuestras estrategias, la siguiente consistirá en hacer demostraciones por contradicción. En pocas palabras para demostrar que una proposición es verdadera, supondremos que no lo es. Y en una serie de pasos lógicos, veremos que habrá proposiciones que son falsas y verdaderas a la vez (esto no puede pasar), llamándose esto una contradicción.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Demuestra directamente que los blorgs rojos comen frutas.
- Demuestra directamente que los blorgs rojos comen frutas los lunes.
- Demuestra indirectamente que si un blorg no come peces, entonces es un blerg.
Entradas relacionadas
- Ir a Álgebra Superior I
- Entrada anterior del curso: Demostraciones matemáticas (el mundo de los Blorg).
- Siguiente entrada del curso: Demostraciones por reducción al absurdo.
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»
