Introducción

Siguiendo la conversación de las funciones, esta vez hablaremos de la composición de funciones. Este es el concepto que nos permitirá combinar más de una función para crear nuevas funciones siempre que ciertas condiciones se cumplan.

Composiciones en relaciones

Anteriormente ya hemos mencionado que sobre tres conjuntos $X,Y,Z$ se puede definir una relación composición entre dos relaciones $R$ de $x$ en $Y$ y $T$ de $Y$ en $Z$. De manera que la relación $T \circ R$ es aquella que está compuesta de elementos de la forma $(x,z) \in X \times Z$ siempre y cuando exista alguna $y$ de manera que $(x,y) \in R$ y $(y,z) in T$. Así, la relación composición está formada de elementos que pueden ir de $X$ a $Y$ mediante la relación $R$ y de ahí pueden llegar a $Z$ mediante la relación $T$. Veremos a continuación cómo podemos traducir esto a las funciones.

Composiciones en funciones

La composición de funciones será una composición de relaciones, no cambiará la definición, pues las funciones siguen siendo relaciones y hemos establecido toda una base sobre lo que son las relaciones para llegar a hablar de las funciones de forma gradual.

Piensa en el siguiente ejemplo. Supongamos tenemos una máquina $f$ que transforma las horas en minutos y otra máquina $g$ que transforma los minutos en segundos. Cuando a la máquina $f$ le pasamos de entrada «$1$ hora», nos regresará «$60$ minutos». Mientras que cuando le pasamos la entrada «$1$ minuto» a la máquina $g$ esta nos devuelve «60 segundos». Ahora nos preguntamos ¿Hay una forma de convertir las horas en segundos? O dicho de otra forma, ¿Cómo podemos construir una máquina $h$ que convierta las horas en los segundos? Nota que no tenemos directamente la máquina que nos toma las horas y las convierte en segundos, pero sí tenemos una máquina que convierte las horas en minutos y después los minutos en segundos.

Supongamos que tenemos la entrada «1 hora» entonces con la máquina $f$ podemos saber que una hora equivale a $60$ minutos. Enseguida podemos usar la máquina $G$ para saber que que los $60$ minutos equivalen a $3600$ segundos, de manera que esa es la duración de una hora. A esta máquina $h$ le llamamos la composición de $f$ con $g$.

Pensemos a estas máquinas como funciones, si consideramos $H$ como al conjunto de número de horas a considerar ($H=\{1 hr, 2 hrs, 3 hrs, \dots\}$) a $M$ como el conjunto de los minutos ($M =\{1 min, 2 mins, 3 mins, \dots\}$) y a $S$ como el conjunto de los segundos a considerar ($S=\{1 seg, 2 segs, 3 segs, \dots\}$) entonces $f:H \rightarrow M$ y $g: M \rightarrow S$ son funciones que convierten una unidad de tiempo en otra. La función $h : H \rightarrow S$ buscada es justamente la composición de las funciones $g \circ f: H \rightarrow S$.

Nota que si queremos convertir un número de horas $n \in H$ a segundos entonces bastará con notar que $n$ horas son $f(n)$ minutos, y estos a su vez son $g(f(n))$ segundos. Veamos el primer ejemplo. Nota que $f(1 hr)=60 mins$. Entonces $g(f(1hr))=g(60min)=3600segs$. Por lo cual la función que convierte las horas a segundos es componer $f$ con $g$.

Composición de funciones

Gráficamente lo que significa la composición de funciones es la siguiente imagen:

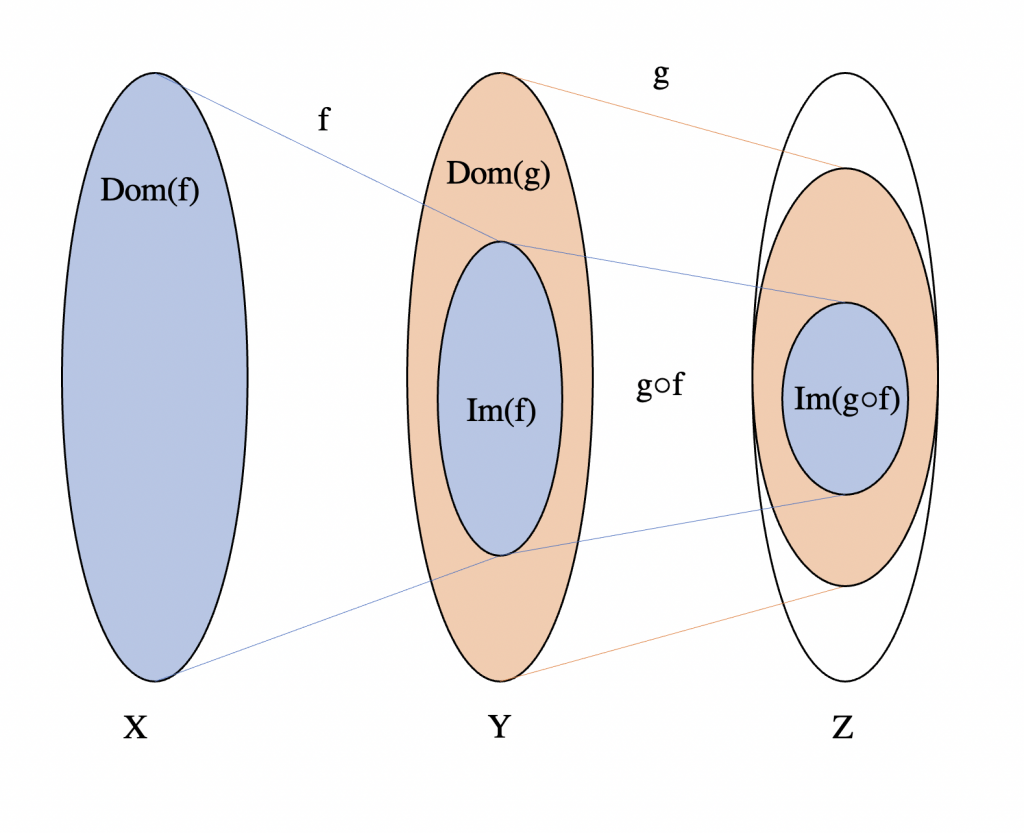
Aquí podemos visualizar la función $g \circ f$ que es la función que va de $X$ a $Z$. En ella, vemos cómo es que la función $f$ va de X a Y, siendo que el dominio de $f$ queda dentro de $Y$, pues por definición, si la función $f$ va de $X$ a $Y$, entonces para cada elemento $x \in X$ sucede que existe $y \in Y$ tal que $f(x)=y$, significando que siempre $Im(f) \subset Y$ , y en nuestro caso en particular, $Y= Dom(g)$, siendo $g$ una función que va de $X$ a $Z$. Quizá lo que no es inmediato es la siguiente contención: $Im(g \circ f) \subset Im(g) \subset Z$.

Proposición. Si $f:X \rightarrow Y $ y $g: Y \rightarrow Z$ entonces $Im(g \circ f) \subset Im(g) \subset Z$

Demostración. Para esta demostración, consideremos $w \in Im(g \circ f) $ y veamos que $w \in Im(g)$. Para ello, notemos que por definición de la composición de funciones, si $w \in. Im(g \circ f)$ entonces existe $x \in X$ tal que $g \circ f(x) = w$. Es decir, $g(f(x))=w$ a su vez, como $f(x) \in Dom(g)$ entonces existe $y$ tal que $f(x)=y$ y $g(y)=w$. Ahora notemos que $y \in Dom(g)$ entonces $g(y) \in Im(g)$, es decir, $w=g(y) \in Dom(g)$. Por otro lado, por definición de función, la imagen de $g$ está contenida en $Z$. De esta manera, se tiene la contención buscada.

$\square$

Vamos a hacer algunas observaciones de esta composición de funciones.

1. Para componer funciones, la imagen de una función debe estar contenida en el dominio de la otra. Esto significa que si queremos componer $f$ con $g$, debemos saber que todo elemento convertido por $f$ puede ser pasado a $g$. Dicho de otra manera, si queremos convertir horas a segundos, la máquina $f$ convierte las horas a minutos, y la $g$ minutos a segundos, entonces siempre tiene que pasar que $f$ devuelva minutos para poder componerse con $g$, pues acepta nada más minutos como entrada, si $f$ convirtiera horas a días, $g$ lo rechazaría, pues un día no está expresado en términos de minutos.
2. La composición de funciones es asociativa, es decir, $(g\circ f) \circ h = g \circ (f \circ h)$.

Demostración. Consideremos $f : X \rightarrow Y$, $g : Y \rightarrow Z$ y $h : W \rightarrow X$. Para demostrar que la función es asociativa, deberíamos demostrar que apra algún $x$ arbitrario en el dominio de la composición $(W)$, se cumple que

$$ (g\circ f) \circ h(x) = g \circ (f \circ h)(x) $$

Para ello, llamemos $f \circ h = F$, $g \circ f = G$,$h(x)=y$ y $f(y)=z$. Ahora, nota por un lado que $$ g \ circ (f \circ h)(x) = g \circ F(x) = g(F(x)) = g(z)$$

Por otro lado, $(g \circ f) \circ h(x) = G \circ h(x) = G(y) = g \circ f(y) = g(z)$

Llegando a los mismos resultados, lo que debe significar que las funciones son iguales para $x$, pudiéndose generalizar para cada elemento del dominio de la composición.

$\square$

Más adelante…

Habiendo visto la composición de funciones, estamos listos para dar el siguiente paso y encontrar una clase muy particular de funciones: funciones invertibles, que serán aquellas funciones que podemos «deshacer».

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Demuestra que si $f$ es suprayectiva, entonces $Im(g \circ f) = Im(g)$.
2. Sea $f: \mathbb{R} \ rightarrow \mathbb{R}$ dada por $f(x)=\frac{3x+1}{2}$:
   1. Encuentra $g: \mathbb{R} \ rightarrow \mathbb{R}$ tal que $g \circ f (x)= x$
   2. Demuestra que $g \circ f = f \circ g$
3. Da condiciones suficientes y necesarias para que $g \circ f$ sea biyectiva.

Entradas relacionadas

• Ir a Álgebra Superior I
• Entrada anterior del curso: Funciones inyectivas, suprayectivas y biyectivas
• Siguiente entrada del curso: Cardinalidad de conjuntos finitos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»