Introducción

En esta entrada daremos algunas definiciones básicas sobre series de números complejos, así como algunos resultados importantes sobre la convergencia de dichas series, por lo que se recomienda revisar los resultados sobre sucesiones de números complejos vistos en la entrada 8 de la primera unidad.

Los resultados de esta entrada serán de utilidad al trabajar con series de funciones y series de potencias en las siguientes entradas.

Definición 27.1. (Serie de números complejos.)
Sea ${\left\{z_n\right\}}_{n\in \mathbb{N}}\subset \mathbb{C}$ una sucesión de números complejos. Una serie infinita de números complejos o simplemente una serie de números complejos es una expresión de la forma: $$\sum _{n=0}^{\mathrm{\infty }}{z}_n,$$ donde $z_n$ es llamado el $(n+1)$-ésimo término de la serie.

Definimos a la sucesión de sumas parciales ${\left\{s_n\right\}}_{n\ge 0}$ como: $$s_n=\sum _{k=0}^n{z}_k=z_0+z_1+\cdots +z_n.$$

Notemos que a cada serie de números complejos $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ le podemos asociar una sucesión de sumas parciales $\left\{s_n\right\}n\ge 0$.

Observación 27.1.
En la entrada 8 trabajamos con sucesiones cuyo subíndice tomaba valores en ${\mathbb{N}}^{+}$, sin embargo, en el caso de las series de números complejos muchas ocasiones será conveniente trabajar con $\mathbb{N}$ (o subconjuntos de este conjunto) como conjunto de índices, es decir, podremos tener series que inicien desde distintos índices como: $$\sum _{n=0}^{\mathrm{\infty }}{z}_n,\sum _{n=1}^{\mathrm{\infty }}{z}_n,\sum _{n=2}^{\mathrm{\infty }}{z}_n,\dots ,\text{etc.}$$

Por lo que, de manera indistinta trabajaremos con estos conjuntos de índices según sea conveniente.

Definición 27.2. (Serie de números complejos convergente.)
Diremos que una serie de números complejos $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ converge, o es convergente, a un número complejo $s$, si la sucesión de sumas parciales ${\left\{s_n\right\}}_{n\ge 0}$ converge a $s$, es decir si para todo $\epsilon >0$ existe $N\in \mathbb{N}$ tal que si $n\ge N$, entonces: $$\left|s_n–s\right|=\left|\sum _{k=0}^n{z}_k–s\right|<\epsilon ,$$ lo cual denotamos como $s=\underset{n\to \mathrm{\infty }}{lim}{s}_n=\sum _{n=0}^{\mathrm{\infty }}{z}_n$. Si la sucesión de sumas parciales no converge o diverge a infinito, diremos que la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ diverge o es divergente.

Observación 27.2.
De acuerdo con la definición anterior, debe ser claro que para el estudio de la convergencia de una serie de números complejos, así como de sus propiedades, utilizaremos los resultados de la entrada 8.

Proposición 27.1. (Criterio de convergencia de Cauchy para series).
Una serie de números complejos $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ es convergentes si y solo si para todo $\epsilon >0$ existe $N=N(\epsilon )\in \mathbb{N}$ tal que si $n,m\ge N$, con $n>m$, entonces:
$$\left|\sum _{k=m+1}^n{z}_k\right|<\epsilon .$$

Demostración. Sea ${\left\{s_n\right\}}_{n\ge 0}$ la sucesión de sumas parciales de la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$.

Notemos que para $n,m\in \mathbb{N}$, con $n>m$, tenemos que:
$$\sum _{k=m+1}^n{z}_k=\sum _{k=0}^n{z}_k-\sum _{k=0}^m{z}_k=s_n–s_m.$$

$⟹)$

Sea $\epsilon >0$. Supongamos que $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ es convergente, entonces la sucesión ${\left\{s_n\right\}}_{n\ge 0}$ converge, por lo que es una sucesión de Cauchy, proposición 8.4, es decir, para el $\epsilon >0$ dado existe $N\in \mathbb{N}$ tal que si $n,m\ge N$, con $n>m$, entonces:
$$|s_n–s_m|<\epsilon .$$ Por lo que:
$$\left|\sum _{k=m+1}^n{z}_k\right|=\left|s_n–s_m\right|<\epsilon .$$

$(⟸$

Sea $\epsilon >0$, entonces existe $N(\epsilon )\in \mathbb{N}$ tal que si $n,m\ge N$, con $n>m$, se cumple que:
$$|s_n–s_m|=\left|\sum _{k=m+1}^n{z}_k\right|<\epsilon .$$

Por lo que, la sucesión de sumas parciales ${\left\{s_n\right\}}_{n\ge 0}$ es de Cauchy. Como $\mathbb{C}$ es completo, proposición 8.5, entonces la sucesión ${\left\{s_n\right\}}_{n\ge 0}$ es convergente, por lo que $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ converge.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Corolario 27.1. (Criterio de divergencia de una serie.)
Si una serie de números complejos $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ converge, entonces $\underset{n\to \mathrm{\infty }}{lim}{z}_n=0$, es decir la sucesión de números complejos ${\left\{z_n\right\}}_{n\ge 0}$ converge a $0$.

Demostración. Dadas las hipótesis, sea $\epsilon >0$.

De la proposición 27.1 se sigue que existe $N\in \mathbb{N}$ tal que si $n,n-1\ge N$, entonces:

$$|z_n–0|=|z_n|=|s_n–s_{n-1}|=\left|\sum _{k=n}^n{z}_k\right|<\epsilon ,$$ es decir $\underset{n\to \mathrm{\infty }}{lim}{z}_n=0$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Observación 27.3.
La utilidad de este corolario es mucha, pues nos permite tener un primer criterio de divergencia al considerar su contrapuesta, es decir si $\underset{n\to \mathrm{\infty }}{lim}{z}_n\ne 0$ ó $\underset{n\to \mathrm{\infty }}{lim}{z}_n=\mathrm{\infty }$, entonces $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ diverge.

Ejemplo 27.1.
Veamos que la serie $\sum _{n=0}^{\mathrm{\infty }}{(1+i)}^n$ es divergente.

Solución. Sea $z_n={(1+i)}^n$ el $(n+1)$-ésimo término de la serie. Notemos que:
$$\underset{n\to \mathrm{\infty }}{lim}|z_n|=\underset{n\to \mathrm{\infty }}{lim}|{(1+i)}^n|=\underset{n\to \mathrm{\infty }}{lim}|1+i{|}^n=\underset{n\to \mathrm{\infty }}{lim}{\left(\sqrt{2}\right)}^n=\mathrm{\infty }.$$ Por lo que, de acuerdo con el ejercicio 6 de la entrada 8, $\underset{n\to \mathrm{\infty }}{lim}{z}_n\ne 0$. Entonces la serie diverge.

Notemos que el recíproco del corolario 27.1 no es válido, es decir, la condición $\underset{n\to \mathrm{\infty }}{lim}{z}_n=0$ no es suficiente para garantizar la convergencia de una serie.

Ejemplo 27.2.
Consideremos la serie armónica:
$$\sum _{n=1}^{\mathrm{\infty }}{z}_n=\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n}.$$

De nuestros cursos de Cálculo sabemos que $\underset{n\to \mathrm{\infty }}{lim}{z}_n=0$. Sin embargo la serie armónica es divergente.

Para verificar esto supongamos que $\sum _{n=0}^{\mathrm{\infty }}{\displaystyle \frac{1}{n}}=L\in \mathbb{R}$.

Notemos que:
$$\begin{array}{rl}L& =1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\cdots \\ & >\frac{1}{2}+\frac{1}{2}+\frac{1}{4}+\frac{1}{4}+\frac{1}{6}+\frac{1}{6}+\cdots \\ & =1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\cdots \\ & =L,\end{array}$$ es decir $L>L$, lo cual claramente no es posible, por lo que la serie diverge.

Para $m\ge 1$ la expresión $\sum _{n=m+1}^{\mathrm{\infty }}{z}_n$ es llamada una cola de la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$. Para un $m$ fijo la cola de una serie es en sí misma una serie, la cual difiere en una cantidad finita de la serie original.

Corolario 27.2.
Una serie de números complejos $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ converge si y solo si su cola $\sum _{n=M}^{\mathrm{\infty }}$ converge, donde $M$ es un número natural fijo.

Demostración. Dadas las hipótesis, consideremos a $s_n=\sum _{k=0}^n{z}_k$ como la $n$-ésima suma parcial de la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$. Definimos:
$$s_n^M=\sum _{k=M}^n{z}_k,$$ como la $n$-ésima suma parcial de la cola $\sum _{n=M}^{\mathrm{\infty }}{z}_n$.

Notemos que si $n,m\ge M$, con $n>m$, entonces:
$$s_n^M–s_m^M=\sum _{k=m+1}^n{z}_n=s_n–s_m.$$

De acuerdo con lo anterior, es claro que el resultado se sigue del criterio de convergencia de Cauchy tomando $M>N$ en la proposición 27.1.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Observación 27.4.
En este punto es importante recordar la convención que establecimos en la observación 4.7, sobre que $z^0=1$ para todo $z\in \mathbb{C}$.

Ejemplo 27.3.
Veamos que la serie geométrica $\sum _{n=0}^{\mathrm{\infty }}{z}^n$ es convergente si $|z|<1$ y en tal caso:
$$\sum _{n=0}^{\mathrm{\infty }}{z}^n=\frac{1}{1-z}.$$ Mientras que la serie diverge si $|z|\ge 1$.

Solución. Consideremos a la $(n+1)$-ésima suma parcial, es decir:
$$s_n=1+z+z^2+\cdots +z^n.$$

Multiplicando por $z$ y sumando 1 en la igualdad anterior tenemos:
$$1+z{s}_n=1+z+z^2+z^3+\cdots +z^{n+1}=s_n+z^{n+1},$$ de donde $s_n(z-1)=z^{n+1}–1$.

Para $z\ne 1$, tenemos que:
$$s_n=\frac{z^{n+1}–1}{z-1}=\frac{1–z^{n+1}}{1-z}=\frac{(1+z+z^2+\cdots +z^n)(1-z)}{(1-z)}.$$

De acuerdo con el ejercicio 4 de la entrada 8, sabemos que la sucesión ${\left\{z^n\right\}}_{n\ge 0}$ converge a $0$ si $|z|<1$ y diverge si $|z|>1$.

Entonces, para $|z|<1$ tenemos que:
$$\underset{n\to \mathrm{\infty }}{lim}{s}_n=\underset{n\to \mathrm{\infty }}{lim}(1+z+z^2+z^3+\cdots +z^n)=\underset{n\to \mathrm{\infty }}{lim}\frac{1–z^{n+1}}{1-z}=\frac{1}{1-z},$$

de donde:
$$\sum _{n=0}^{\mathrm{\infty }}{z}^n=\frac{1}{1-z},\text{si}|z|<1.$$

Es claro que en nuestro desarrollo anterior la condición $z\ne 1$ es necesaria y está dada si $|z|\ne 1$, pero ¿qué pasa si $|z|=1$?

Si $|z|=1$, entonces:
$$\underset{n\to \mathrm{\infty }}{lim}\left|z^n\right|=\underset{n\to \mathrm{\infty }}{lim}{\left|z\right|}^n=1\ne 0,$$ por lo que, de acuerdo con el ejercicio 6 de la entrada 8, $\underset{n\to \mathrm{\infty }}{lim}{z}^n\ne 0$, entonces si $|z|\ge 1$ la serie diverge.

Podemos visualizar la convergencia o divergencia de la serie geométrica en el plano complejo $\mathbb{C}$ mediante el siguiente Applet en GeoGebra: https://www.geogebra.org/m/jj65zt24.

La serie geométrica suele aparecer en muchos problemas prácticos, por lo que conocer su región de convergencia nos es de gran utilidad.

Ejemplo 27.4.
Obtengamos la mayor región de convergencia de la serie $\sum _{n=0}^{\mathrm{\infty }}{(4+2z)}^{-n}$. Después determinemos el valor al que converge.

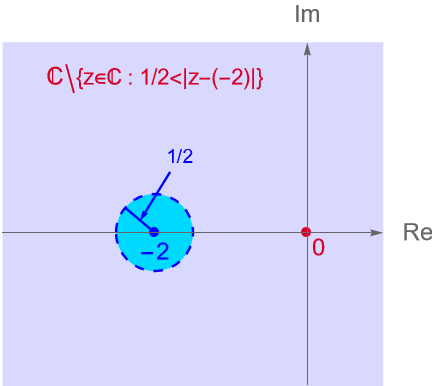
Solución. Primeramente notemos que si $z=-2$, entonces la expresión en el denominador se anula, por lo que dicho punto no puede estar en la región de convergencia de la serie.

Por otra parte, si hacemos $w={\displaystyle \frac{1}{4+2z}}$, entonces la serie dada tiene la forma de una serie geométrica $\sum _{n=0}^{\mathrm{\infty }}{w}^n$.

De acuerdo con el ejemplo anterior, sabemos que la serie geométrica $\sum _{n=0}^{\mathrm{\infty }}{w}^n$ converge a ${\displaystyle \frac{1}{1-w}}$ si $|w|<1$.

Tenemos que:
$$|w|<1⟺\left|\frac{1}{4+2z}\right|<1⟺1<|4+2z|⟺\frac{1}{2}<|z-(-2)|.$$

De acuerdo con los resultados de la entrada 6, sabemos que este conjunto corresponde con los puntos en el plano complejo que caen fuera de la circunferencia centrada en el punto $-2$ y de radio $\frac{1}{2}$, es decir, los $z\in \mathbb{C}$ tales que su distancia al punto $-2$ es estrictamente mayor que $\frac{1}{2}$. Bajo esta condición es claro que $z\ne -2$, figura 105.

Entonces, la región de convergencia de la serie está dada por los $z\in \mathbb{C}$ tales que $\frac{1}{2}<|z-(-2)|$. Para dichos $z$ se tiene que:
$$\sum _{n=0}^{\mathrm{\infty }}\frac{1}{{(4+2z)}^n}={\displaystyle \frac{1}{1–{\displaystyle \frac{1}{4+2z}}}}={\displaystyle \frac{4+2z}{3+2z}}.$$

Proposición 27.2.
Sean $\sum _{n=0}^{\mathrm{\infty }}{z}_n$, $\sum _{n=0}^{\mathrm{\infty }}{w}_n$ dos series de números complejos convergentes y $\alpha ,\beta \in \mathbb{C}$ constantes. Entonces:

1. $\sum _{n=0}^{\mathrm{\infty }}(\alpha z_n\pm \beta w_n)=\alpha \sum _{n=0}^{\mathrm{\infty }}{z}_n\pm \beta \sum _{n=0}^{\mathrm{\infty }}{w}_n$.
2. La serie $\sum _{n=0}^{\mathrm{\infty }}\overline{z_n}$ converge y $\overline{\sum _{n=0}^{\mathrm{\infty }}{z}_n}=\sum _{n=0}^{\mathrm{\infty }}\overline{z_n}$.

Demostración. Dadas las hipótesis.

1. Se deja como ejercicio al lector.
2. Sea $\epsilon >0$. Como la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ converge, digamos a $s\in \mathbb{C}$, tenemos que existe $N\in \mathbb{N}$ tal que si $n\ge N$, entonces: $$\left|\sum _{k=0}^n\overline{z_k}–\bar{s}\right|=\left|\overline{\sum _{k=0}^n{z}_k}–\bar{s}\right|=\left|\overline{\sum _{k=0}^n{z}_k–s}\right|=\left|\sum _{k=0}^n{z}_k–s\right|=\left|s_n–s\right|<\epsilon ,$$ es decir $\overline{\sum _{n=0}^{\mathrm{\infty }}{z}_n}=\sum _{n=0}^{\mathrm{\infty }}\overline{z_n}=\bar{s}\in \mathbb{C}$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Ejemplo 27.5.
Estudiemos la convergencia de la serie $\sum _{n=3}^{\mathrm{\infty }}{\left({\displaystyle \frac{i}{2}}\right)}^n$.

Solución. Tenemos que:
$$\begin{array}{rl}\sum _{n=3}^{\mathrm{\infty }}{\left(\frac{i}{2}\right)}^n=\sum _{n=3}^{\mathrm{\infty }}{\left(\frac{i}{2}\right)}^3{\left(\frac{i}{2}\right)}^{n-3}& ={\left(\frac{i}{2}\right)}^3\sum _{n=3}^{\mathrm{\infty }}{\left(\frac{i}{2}\right)}^{n-3},\text{proposición 27.2,}\\ & ={\left(\frac{i}{2}\right)}^3\sum _{k=0}^{\mathrm{\infty }}{\left(\frac{i}{2}\right)}^k,\text{cambio de índice}k=n-3,\\ & ={\left(\frac{i}{2}\right)}^3\left(\frac{1}{1-{\displaystyle \frac{i}{2}}}\right),\left|\frac{i}{2}\right|=\frac{1}{2}<1,\\ & =\frac{1}{20}(1-2i).\end{array}$$

Corolario 27.3.
Sea $z_n=x_n+i{y}_n\in \mathbb{C}$, con $x_n,y_n\in \mathbb{R}$, para todo $n\in \mathbb{N}$. Entonces, la serie de números complejos $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ converge a $s=x+iy\in \mathbb{C}$ si y solo si las series de números reales $\sum _{n=0}^{\mathrm{\infty }}{x}_n$ y $\sum _{n=0}^{\mathrm{\infty }}{y}_n$ convergen a $x$ y a $y$, respectivamente. En tal caso:
$$\sum _{n=0}^{\mathrm{\infty }}{z}_n=\sum _{n=0}^{\mathrm{\infty }}{x}_n+i\sum _{n=0}^{\mathrm{\infty }}{y}_n.$$

Demostración. De acuerdo con la proposición 8.3, tenemos que:
$$\begin{array}{rl}\sum _{n=0}^{\mathrm{\infty }}{z}_n=s& ⟺\sum _{n=0}^{\mathrm{\infty }}(x_n+i{y}_n)=x+iy,\\ & ⟺\underset{n\to \mathrm{\infty }}{lim}{s}_n=\underset{n\to \mathrm{\infty }}{lim}(\sum _{k=0}^n{x}_k+i\sum _{k=0}^n{y}_k)=x+iy,\\ & ⟺\underset{n\to \mathrm{\infty }}{lim}\sum _{k=0}^n{x}_k=x\text{y}\underset{n\to \mathrm{\infty }}{lim}\sum _{k=0}^n{y}_k=y,\\ & ⟺\sum _{n=0}^{\mathrm{\infty }}{x}_n=x\text{y}\sum _{n=0}^{\mathrm{\infty }}{y}_n=y,\\ & ⟺\sum _{n=0}^{\mathrm{\infty }}{x}_n+i\sum _{n=0}^{\mathrm{\infty }}{y}_n=\sum _{n=0}^{\mathrm{\infty }}(x_n+i{y}_n)=\sum _{n=0}^{\mathrm{\infty }}{z}_n.\end{array}$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Observación 27.5.
Del corolario anterior se sigue que para toda serie convergente de números complejos, $\sum _{n=0}^{\mathrm{\infty }}{z}_n$, se cumple que:
$$\mathrm{Re}\left(\sum _{n=0}^{\mathrm{\infty }}{z}_n\right)=\sum _{n=0}^{\mathrm{\infty }}\mathrm{Re}(z_n)\text{e}\mathrm{Im}\left(\sum _{n=0}^{\mathrm{\infty }}{z}_n\right)=\sum _{n=0}^{\mathrm{\infty }}\mathrm{Im}(z_n).$$

Ejemplo 27.6.
Estudiemos la convergencia de la serie:
$$\sum _{n=0}^{\mathrm{\infty }}{z}_n=\sum _{n=0}^{\mathrm{\infty }}(\frac{1}{2^n}+\frac{i}{3^n}).$$

Solución. Notemos que el $(n+1)$-ésimo término de la serie es $z_n={\displaystyle \frac{1}{2^n}}+{\displaystyle \frac{i}{3^n}}$, por lo que:
$$\mathrm{Re}(z_n)=\frac{1}{2^n},\mathrm{Im}(z_n)=\frac{1}{3^n}.$$

De lo anterior es claro que las dos series reales, correspondientes a las partes real e imaginaria de la serie, son ambas series geométricas convergentes, es decir:
$$\sum _{n=0}^{\mathrm{\infty }}\mathrm{Re}(z_n)=\sum _{n=0}^{\mathrm{\infty }}\frac{1}{2^n}=\frac{1}{1-{\displaystyle \frac{1}{2}}}=2,$$
$$\sum _{n=0}^{\mathrm{\infty }}\mathrm{Im}(z_n)=\sum _{n=0}^{\mathrm{\infty }}\frac{1}{3^n}=\frac{1}{1-{\displaystyle \frac{1}{3}}}=\frac{3}{2}.$$

Por lo tanto, del corolario 27.2 se sigue que la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ es convergente y su suma es:
$$\sum _{n=0}^{\mathrm{\infty }}{z}_n=\sum _{n=0}^{\mathrm{\infty }}(\frac{1}{2^n}+\frac{i}{3^n})=\sum _{n=0}^{\mathrm{\infty }}\frac{1}{2^n}+i\sum _{n=0}^{\mathrm{\infty }}\frac{1}{3^n}=2+i\frac{3}{2}.$$

Definición 27.3. (Serie absolutamente convergente.)
Una serie de números complejos $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ es absolutamente convergente si la serie $\sum _{n=0}^{\mathrm{\infty }}|z_n|$ es convergente.

Definición 29.4. (Serie condicionalmente convergente.)
Una serie de números complejos $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ es condicionalmente convergente si la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ es convergente, pero no es absolutamente convergente.

Proposición 27.3.
Una serie de números complejos $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ absolutamente convergente, es convergente y cumple que:
$$\left|\sum _{n=0}^{\mathrm{\infty }}{z}_n\right|\le \sum _{n=0}^{\mathrm{\infty }}|z_n|.$$

Demostración.
Dadas las hipótesis, sea ${\left\{s_n\right\}}_{n\ge 0}$ la sucesión de sumas parciales de la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$.

Sea $\epsilon >0$. De acuerdo con el criterio de convergencia de Cauchy, proposición 27.1, tenemos que existe $N\in \mathbb{N}$ tal que si $n,m\ge N$, con $n>m$, entonces:
$$\sum _{k=m+1}^n|z_k|=\left|\sum _{k=m+1}^n|z_k|\right|<\epsilon .$$

Por la desigualdad del triángulo, observación 3.6 entrada 3, se cumple que:
$$|s_n–s_m|=\left|\sum _{k=0}^n{z}_k–\sum _{k=0}^m{z}_k\right|=\left|\sum _{k=m+1}^n{z}_k\right|\le \sum _{k=m+1}^n|z_k|<\epsilon ,$$ es decir que la sucesión de sumas parciales ${\left\{s_n\right\}}_{n\ge 0}$ es de Cauchy, por lo que, al ser $\mathbb{C}$ un espacio métrico completo, proposición 8.5, se tiene que la sucesión ${\left\{s_n\right\}}_{n\ge 0}$ es convergente, entonces la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ converge.

De acuerdo con el ejercicio 3 de la entrada 8, sabemos que si una sucesión ${\left\{w_n\right\}}_{n\ge 0}$ converge a $w\in \mathbb{C}$, entonces la sucesión ${\left\{|w_n|\right\}}_{n\ge 0}$ converge a $|w|$.

Como la sucesión ${\left\{s_n\right\}}_{n\ge 0}$ converge, digamos a $s\in \mathbb{C}$, entonces:
$$\underset{n\to \mathrm{\infty }}{lim}|s_n|=\underset{n\to \mathrm{\infty }}{lim}\left|\sum _{k=0}^n{z}_k\right|=\left|\sum _{n=0}^{\mathrm{\infty }}{z}_n\right|=|s|.$$

Análogamente, como la serie $\sum _{n=0}^{\mathrm{\infty }}|z_n|$ es convergente, tenemos que:
$$\underset{n\to \mathrm{\infty }}{lim}\left|\sum _{k=0}^n|z_k|\right|=\underset{n\to \mathrm{\infty }}{lim}\sum _{k=0}^n|z_k|=\sum _{n=0}^{\mathrm{\infty }}|z_n|.$$

Nuevamente, de la desigualdad del triángulo, observación 3.6, se sigue que:
$$\left|\sum _{k=0}^n{z}_k\right|\le \sum _{k=0}^n|z_k|.$$

Considerando lo anterior y el ejercicio 8 de la entrada 8, concluimos que:
$$\left|\sum _{n=0}^{\mathrm{\infty }}{z}_n\right|\le \sum _{n=0}^{\mathrm{\infty }}|z_n|.$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Corolario 27.4.
Sea $z_n=x_n+i{y}_n\in \mathbb{C}$, con $x_n,y_n\in \mathbb{R}$, para todo $n\in \mathbb{N}$. Entonces, la serie de números complejos $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ converge absolutamente a $s=x+iy\in \mathbb{C}$ si y solo si las series de números reales $\sum _{n=0}^{\mathrm{\infty }}{x}_n$ y $\sum _{n=0}^{\mathrm{\infty }}{y}_n$ convergen absolutamente a $x$ y a $y$, respectivamente. En tal caso:
$$\sum _{n=0}^{\mathrm{\infty }}{z}_n=\sum _{n=0}^{\mathrm{\infty }}{x}_n+i\sum _{n=0}^{\mathrm{\infty }}{y}_n.$$

Demostración. Se deja como ejercicio al lector.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Proposición 27.4. (Criterio de comparación de Weierstrass.)
Sea ${\left\{a_n\right\}}_{n\ge 0}$ una sucesión de números reales no negativos y sea ${\left\{z_n\right\}}_{n\ge 0}$ una sucesión de números complejos. Supongamos que $|z_n|\le a_n$ para todo $n\ge j$, para algún $j\in \mathbb{N}$.

1. Si la serie $\sum _{n=0}^{\mathrm{\infty }}{a}_n$ converge, entonces la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ es absolutamente convergente.
2. Si la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ diverge, entonces la serie $\sum _{n=0}^{\mathrm{\infty }}{a}_n$ es divergente.

Demostración. Dadas las hipótesis, sea ${\left\{s_n\right\}}_{n\ge 0}$ la sucesión de sumas parciales de la serie $\sum _{n=0}^{\mathrm{\infty }}|z_n|$.

1. Sea $\epsilon >0$. Por el criterio de Cauchy, proposición 27.1, tenemos que existe $N\in \mathbb{N}$ tal que si $n>m\ge N>j$, entonces:
   $$\left|s_n–s_m\right|=\left|\sum _{k=m+1}^n|z_k|\right|=\sum _{k=m+1}^n|z_k|\le \sum _{k=m+1}^n{a}_k=\left|\sum _{k=m+1}^n{a}_k\right|<\epsilon ,$$ es decir, la sucesión ${\left\{s_n\right\}}_{n\ge 0}$ es de Cauchy, por lo que, al ser $\mathbb{C}$ un espacio métrico completo, la sucesión de sumas parciales converge, entonces la serie $\sum _{n=0}^{\mathrm{\infty }}|z_n|$ converge y por tanto la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ es absolutamente convergente.
2. Es la contrapuesta del caso anterior.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Ejemplo 27.7.
Veamos que las siguientes series son convergentes.
a) ${\displaystyle \sum _{n=0}^{\mathrm{\infty }}{\displaystyle \frac{3+2i}{{(n+1)}^n}}}$.
b) ${\displaystyle \sum _{n=0}^{\mathrm{\infty }}{\displaystyle \frac{2\cos (n\theta )+i2\mathrm{sen}(n\theta )}{n^2+3}}}$.

Solución.

a) Procedemos a probar la convergencia de la serie utilizando el criterio de comparación. Para ello consideremos a la serie geométrica:
$$\sum _{n=0}^{\mathrm{\infty }}\frac{1}{2^n},$$ la cual es convergente.

Notemos que:
$$|3+2i|=\sqrt{3^2+2^2}=\sqrt{13}<4,$$

por lo que:
$$\left|\frac{3+2i}{{(n+1)}^n}\right|=\frac{|3+2i|}{{(n+1)}^n}=\frac{\sqrt{13}}{{(n+1)}^n}<\frac{4}{{(n+1)}^n}.$$

Por otra parte, es sencillo verificar que para $n\ge 3$ se cumple que:
$$\left|\frac{3+2i}{{(n+1)}^n}\right|<\frac{4}{{(n+1)}^n}<\frac{1}{2^n},$$

por lo que se deja como ejercicio al lector.

Entonces, por el criterio de comparación, concluimos que la serie dada es absolutamente convergente y por tanto converge.

b) De nueva cuenta, procedemos a probar la convergencia de la serie utilizando el criterio de comparación. Consideremos a la serie convergente:
$$\sum _{n=1}^{\mathrm{\infty }}\frac{2}{n^2}.$$

Notemos que:
$$\left|{\displaystyle \frac{2\cos (n\theta )+i2\mathrm{sen}(n\theta )}{n^2+3}}\right|\le {\displaystyle \frac{2|\cos (n\theta )+i\mathrm{sen}(n\theta )|}{n^2}}={\displaystyle \frac{2}{n^2}}.$$

Entonces, por el criterio de comparación, concluimos que la serie:
$$\sum _{n=1}^{\mathrm{\infty }}{\displaystyle \frac{2\cos (n\theta )+i2\mathrm{sen}(n\theta )}{n^2+3}},$$

es convergente, por lo que, de acuerdo con el corolario 27.2, la serie original converge.

Proposición 27.5. (Criterio de la razón o del cociente de D’Alembert.)
Sea ${\left\{z_n\right\}}_{n\ge 0}$ una sucesión de números complejos distintos de cero, tales que:
$$\underset{n\to \mathrm{\infty }}{lim}\frac{|z_{n+1}|}{|z_n|}=\lambda ,$$ existe o es infinito.

1. Si $\lambda <1$, entonces la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ es absolutamente convergente.
2. Si $\lambda >1$ ó $\lambda =\mathrm{\infty }$, entonces la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ es divergente.
3. Si $\lambda =1$, entonces la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ puede diverger o converger.

Demostración. Dadas las hipótesis, como $z_n\ne 0$ para todo $n\in \mathbb{N}$, entonces:
$$\left|\frac{z_{n+1}}{z_n}\right|=\frac{|z_{n+1}|}{|z_n|}>0,\mathrm{\forall }n\in \mathbb{N}.$$

De lo anterior es claro que si $\underset{n\to \mathrm{\infty }}{lim}{\displaystyle \frac{|z_{n+1}|}{|z_n|}}=\lambda \in \mathbb{R}$, entonces $\lambda \ge 0$.

1. Supongamos que $\lambda \in \mathbb{R}$ con $0\le \lambda <1$. Sea $r={\displaystyle \frac{\lambda +1}{2}}$, entonces $0\le \lambda <r<1$.
   Para $\epsilon =r–\lambda >0$, tenemos que existe $N\in \mathbb{N}$ tal que si $n\ge N$, entonces: $$\left|\left|\frac{z_{n+1}}{z_n}\right|–\lambda \right|<\epsilon ⟹\frac{|z_{n+1}|}{|z_n|}<\epsilon +\lambda =r,$$ de donde se sigue que: $$|z_{n+1}|<r|z_n|\mathrm{\forall }n\ge N.$$ Considerando lo anterior, para $n\ge N$ tenemos que: $$\begin{array}{rl}|z_{N+1}|& <r|z_N|\\ |z_{N+2}|& <r|z_{N+1}|<r^2|z_N|\\ |z_{N+3}|& <r|z_{N+2}|<r^3|z_N|\\ & ⋮\\ |z_n|& <r^{n-N}|z_N|\\ & ⋮\end{array}$$ Dado que $r<1$, notemos que: $$\sum _{n=N}^{\mathrm{\infty }}{r}^{n-N}=\sum _{k=0}^{\mathrm{\infty }}{r}^k,$$ es una serie geométrica convergente. Por lo que, de acuerdo con la proposición 27.2, tenemos que la serie $\sum _{n=N}^{\mathrm{\infty }}{r}^{n-N}|z_N|$ converge, entonces por el criterio de comparación se sigue que la serie $\sum _{n=N}^{\mathrm{\infty }}|z_n|$ converge y por el corolario 27.2 concluimos que la serie $\sum _{n=0}^{\mathrm{\infty }}|z_n|$ converge.
   
   Entonces, la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ es absolutamente convergente y por tanto converge, proposición 27.3.
2. Supongamos que $\lambda >1$. Sea $r={\displaystyle \frac{\lambda +1}{2}}$, el cual cumple que $1<r<\lambda$. Procediendo como en el caso anterior, para $\epsilon =\lambda –r>0$ existe $N\in \mathbb{N}$ tal que si $n\ge N$ entonces: $$|z_{n+1}|>r|z_n|,$$ de donde se sigue que: $$|z_n|>r^{n-N}|z_N|>0,\mathrm{\forall }n\ge N,$$ por lo que $\underset{n\to \mathrm{\infty }}{lim}|z_n|\ne 0$, entonces $\underset{n\to \mathrm{\infty }}{lim}{z}_n\ne 0$ y por tanto la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ es divergente, corolario 27.1.
   
   Análogamente, si $\lambda =\mathrm{\infty }$, tenemos que para todo $M>0$ existe un $N\in \mathbb{N}$ tal que si $n\ge N$ entonces: $$|z_n|>M^{n-N}|z_N|>0,$$ de donde se sigue que la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ diverge.
3. Consideremos a las series: $$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n}\text{y}\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2}.$$ Para ambas se cumple que $z_n\ne 0$ para todo $n\in {\mathbb{N}}^{+}$ y que: $$\underset{n\to \mathrm{\infty }}{lim}\frac{{\displaystyle \frac{1}{n+1}}}{{\displaystyle \frac{1}{n}}}=\underset{n\to \mathrm{\infty }}{lim}\frac{n}{n+1}=1=\lambda .$$ $$\underset{n\to \mathrm{\infty }}{lim}\frac{{\displaystyle \frac{1}{(n+1{)}^2}}}{{\displaystyle \frac{1}{n^2}}}=\underset{n\to \mathrm{\infty }}{lim}\frac{n^2}{(n+1{)}^2}=1=\lambda .$$ Sin embargo, de acuerdo con el ejemplo 27.2, sabemos que la primera serie diverge, mientras que, utilizando el criterio de comparación y la serie ${\displaystyle \sum _{n=2}^{\mathrm{\infty }}{\displaystyle \frac{1}{n^2–n}}}$, se puede verificar que la segunda serie converge. Entonces, si $\lambda =1$ el criterio no es concluyente.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Ejemplo 27.8.
Sea $z\in \mathbb{C}$. Estudiemos la convergencia de la serie $\sum _{n=0}^{\mathrm{\infty }}{\displaystyle \frac{z^n}{n!}}$.

Solución. Sea $z_n={\displaystyle \frac{z^n}{n!}}$, entonces $|z_n|={\displaystyle \frac{|z{|}^n}{n!}}\ge 0$. Si $z=0$, es claro que la serie converge.

Supongamos que $z\ne 0$, entonces $z_n\ne 0$ para todo $n\in \mathbb{N}$. Tenemos que:
$$\underset{n\to \mathrm{\infty }}{lim}\frac{\left|z_{n+1}\right|}{\left|z_n\right|}=\underset{n\to \mathrm{\infty }}{lim}\frac{{\displaystyle \frac{{\left|z\right|}^{n+1}}{(n+1)!}}}{{\displaystyle \frac{{\left|z\right|}^n}{n!}}}=\underset{n\to \mathrm{\infty }}{lim}\frac{\left|z\right|}{n+1}=0<1,$$

por lo que la serie $\sum _{n=0}^{\mathrm{\infty }}{\displaystyle \frac{z^n}{n!}}$ es absolutamente convergente para todo $z\in \mathbb{C}$.

Ejemplo 27.9.
Analicemos el comportamiento de las siguientes series.
a) ${\displaystyle \sum _{n=0}^{\mathrm{\infty }}{\displaystyle \frac{(1-i{)}^n}{n!}}}$.
b) ${\displaystyle \sum _{n=0}^{\mathrm{\infty }}{\displaystyle \frac{(z-i{)}^n}{2^n}}}$.

Solución.

a) Sea $z_n={\displaystyle \frac{(1-i{)}^n}{n!}}$ el $(n+1)$-ésimo término de la serie. Claramente $z_n\ne 0$ para toda $n\in \mathbb{N}$.

Considerando el criterio de la razón, proposición 27.5, tenemos que:
$$\begin{array}{rl}\lambda =\underset{n\to \mathrm{\infty }}{lim}\frac{\left|z_{n+1}\right|}{\left|z_n\right|}=\underset{n\to \mathrm{\infty }}{lim}\left|\frac{{\displaystyle \frac{(1-i{)}^{n+1}}{(n+1)!}}}{{\displaystyle \frac{(1-i{)}^n}{n!}}}\right|& =\underset{n\to \mathrm{\infty }}{lim}\left|\frac{(1-i{)}^{n+1}n!}{(1-i{)}^n(n+1)n!}\right|\\ & =\underset{n\to \mathrm{\infty }}{lim}\frac{|1-i|}{n+1}\\ & =\underset{n\to \mathrm{\infty }}{lim}\frac{\sqrt{2}}{n+1}\\ & =0.\end{array}$$ Como $\lambda <1$, entonces la serie converge.

b) Sea $z_n={\displaystyle \frac{(z-i{)}^n}{2^n}}$ el $(n+1)$-ésimo término de la serie. Notemos que si $z=i$, entonces la serie converge.

Supongamos que $z\ne i$, entonces para todo $n\in \mathbb{N}$ se cumple que $z_n\ne 0$. Tenemos que:
$$\begin{array}{rl}\lambda =\underset{n\to \mathrm{\infty }}{lim}\frac{\left|z_{n+1}\right|}{\left|z_n\right|}=\underset{n\to \mathrm{\infty }}{lim}\left|\frac{{\displaystyle \frac{(z-i{)}^{n+1}}{2^{n+1}}}}{{\displaystyle \frac{(z-i{)}^n}{2^n}}}\right|& =\underset{n\to \mathrm{\infty }}{lim}\left|\frac{2^n(z-i{)}^{n+1}}{2^{n+1}(z-i{)}^n}\right|\\ & =\underset{n\to \mathrm{\infty }}{lim}\frac{|z-i|}{2}\\ & =\frac{|z-i|}{2}.\end{array}$$

Por el criterio de la razón, proposición 27.5, tenemos que $\lambda <1$ si $|z-i|<2$, en tal caso la serie converge.

Por otra parte, $\lambda >1$ si $|z-i|>2$, en tal caso la serie diverge.

Por último, tenemos que:
$$|z-i|<2⟹\left|\frac{z-i}{2}\right|<1,$$

es decir, la serie dada es una serie geométrica convergente si $|z-i|<2$, en tal caso:
$$\sum _{n=0}^{\mathrm{\infty }}{\displaystyle \frac{(z-i{)}^n}{2^n}}=\sum _{n=0}^{\mathrm{\infty }}{\left({\displaystyle \frac{z-i}{2}}\right)}^n=\frac{1}{1–{\displaystyle \frac{z-i}{2}}}=\frac{2}{2-(z–i)}.$$

Y para $|z-i|\ge 2$ la serie diverge.

Proposición 27.6. (Criterio de la raíz.)
Sea ${\left\{z_n\right\}}_{n\ge 0}$ una sucesión de números complejos, tales que:
$$\underset{n\to \mathrm{\infty }}{lim}=|z_n{|}^{1/n}=\lambda ,$$ existe o es infinito.

1. Si $\lambda <1$, entonces la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ es absolutamente convergente.
2. Si $\lambda >1$ ó $\lambda =\mathrm{\infty }$, entonces la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ es divergente.
3. Si $\lambda =1$, entonces la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ puede diverger o converger.

Demostración. La prueba es análoga a la de la proposición 27.5, por lo que los detalles se dejan como ejercicio al lector.

Dadas las hipótesis.

1. Supongamos que $\lambda \in \mathbb{R}$ con $0\le \lambda <1$. Elegimos a $r\in \mathbb{R}$ tal que $\lambda <r<1$. Tenemos que existe $N\in \mathbb{N}$ tal que si $n\ge N$, entonces: $${\left|z_n\right|}^{1/n}<r⟹\left|z_n\right|<r^n.$$ Dado que $r<1$, tenemos que la serie geométrica $\sum _{n=N}^{\mathrm{\infty }}{r}^n$ converge, entonces por el criterio de comparación se sigue que la serie $\sum _{n=N}^{\mathrm{\infty }}|z_n|$ converge y por el corolario 27.2 concluimos que la serie $\sum _{n=0}^{\mathrm{\infty }}|z_n|$ converge.
   
   Entonces, la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ es absolutamente convergente y por tanto converge.
2. Si $\lambda >1$ ó $\lambda =\mathrm{\infty }$. Tomemos a $r\in \mathbb{R}$ tal que $1<r<\lambda$. Tenemos que existe $N\in \mathbb{N}$ tal que si $n\ge N$, entonces: $${\left|z_n\right|}^{1/n}>r⟹\left|z_n\right|>r^n>1.$$ Por lo que $\underset{n\to \mathrm{\infty }}{lim}{z}_n\ne 0$ y por tanto la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ es divergente.
3. Consideremos a las series: $$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n}\text{y}\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^2}.$$ Para ambas se cumple que: $$\underset{n\to \mathrm{\infty }}{lim}{\left|\frac{1}{n}\right|}^{1/n}=\underset{n\to \mathrm{\infty }}{lim}{\left(\frac{1}{n}\right)}^{1/n}1=\lambda .$$ $$\underset{n\to \mathrm{\infty }}{lim}{\left|\frac{1}{n^2}\right|}^{1/n}=\underset{n\to \mathrm{\infty }}{lim}{\left(\frac{1}{n^2}\right)}^{1/n}1=\lambda .$$ Sin embargo, la primera serie diverge, mientras que la segunda serie converge. Entonces, si $\lambda =1$ el criterio no es concluyente.

En general, el criterio de la razón es más fácil de aplicar que el criterio de la raíz, aunque existen ciertos casos donde la forma de la sucesión hace evidente el uso del criterio de la raíz.

Ejemplo 27.10.
Analicemos el comportamiento de las siguientes series.
a) ${\displaystyle \sum _{n=0}^{\mathrm{\infty }}{\displaystyle \frac{z^n}{(n+1{)}^n}}}$.
b) ${\displaystyle \sum _{n=0}^{\mathrm{\infty }}{\displaystyle \frac{(1+i{)}^n}{3^n}}}$.

Solución.

a)] Sea $z_n={\left({\displaystyle \frac{z}{n+1}}\right)}^n$ el $(n+1)$-ésimo término de la sucesión, entonces:
$$\lambda =\underset{n\to \mathrm{\infty }}{lim}{\left|z_n\right|}^{1/n}=\underset{n\to \mathrm{\infty }}{lim}{\left|{\left({\displaystyle \frac{z}{n+1}}\right)}^n\right|}^{1/n}=\underset{n\to \mathrm{\infty }}{lim}{\displaystyle \frac{\left|z\right|}{n+1}}=0.$$

Como $\lambda <1$, entonces por el criterio de la raíz tenemos que la serie converge.

b) Sea $z_n={\left({\displaystyle \frac{1+i}{3}}\right)}^n$ el $(n+1)$-ésimo término de la sucesión, entonces:
$$\lambda =\underset{n\to \mathrm{\infty }}{lim}{\left|z_n\right|}^{1/n}=\underset{n\to \mathrm{\infty }}{lim}{\left|{\left({\displaystyle \frac{1+i}{3}}\right)}^n\right|}^{1/n}=\underset{n\to \mathrm{\infty }}{lim}{\displaystyle \frac{|1+i|}{3}}=\frac{\sqrt{2}}{3}.$$

Como $\lambda <1$, entonces por el criterio de la raíz tenemos que la serie converge.

Dado que $\left|{\displaystyle \frac{1+i}{3}}\right|<1$, entonces la serie es geométrica, por lo que:
$$\sum _{n=0}^{\mathrm{\infty }}{\displaystyle \frac{(1+i{)}^n}{3^n}}=\frac{1}{1-{\displaystyle \frac{1+i}{3}}}=\frac{3}{2-i}.$$

Definición 27.5. (Producto de Cauchy para series.)
Sean $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ y $\sum _{n=0}^{\mathrm{\infty }}{w}_n$ dos series de números complejos. Definimos el producto de ambas series como la serie $\sum _{n=0}^{\mathrm{\infty }}{c}_n$ cuyo $n$-ésimo término está dado como:
$$\begin{array}{}\text{(27.1)}& c_n=z_0{w}_n+z_1{w}_{n-1}+\cdots +z_{n-1}{w}_1+z_n{w}_0=\sum _{k=0}^n{z}_k{w}_{n-k}.\end{array}$$

La serie:
$$\begin{array}{}\text{(27.2)}& \sum _{n=0}^{\mathrm{\infty }}{c}_n=\sum _{n=0}^{\mathrm{\infty }}\left(\sum _{k=0}^n{z}_k{w}_{n-k}\right).\end{array}$$ es llamada el producto de Cauchy de las series $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ y $\sum _{n=0}^{\mathrm{\infty }}{w}_n$.

Ejemplo 27.11.
Sean $z,w\in \mathbb{C}$. Obtengamos el producto de Cauchy de las series:
$$\sum _{n=0}^{\mathrm{\infty }}\frac{z^n}{n!}\text{y}\sum _{n=0}^{\mathrm{\infty }}\frac{w^n}{n!}.$$

Solución. Sean $z_n={\displaystyle \frac{z^n}{n!}}$ y $w_n={\displaystyle \frac{w^n}{n!}}$ para todo $n\in \mathbb{N}$. De acuerdo con (29.2) tenemos que:
$$\begin{array}{rl}\sum _{n=0}^{\mathrm{\infty }}{c}_n=\sum _{n=0}^{\mathrm{\infty }}\left(\sum _{k=0}^n{z}_k{w}_{n-k}\right)& =\sum _{n=0}^{\mathrm{\infty }}\left(\sum _{k=0}^n\frac{z^k}{k!}\frac{w^{n-k}}{(n-k)!}\right)\\ & =\sum _{n=0}^{\mathrm{\infty }}\frac{1}{n!}\left(\sum _{k=0}^n\frac{n!}{k!(n-k)!}{z}^k{w}^{n-k}\right)\\ & =\sum _{n=0}^{\mathrm{\infty }}\frac{1}{n!}\left(\sum _{k=0}^n(\genfrac{}{}{0ex}{}{n}{k})z^k{w}^{n-k}\right)\\ & =\sum _{n=0}^{\mathrm{\infty }}\frac{(z+w{)}^n}{n!}.\end{array}$$

Como hemos visto hasta ahora, las series absolutamente convergentes heredan propiedades de convergencia que resultan de gran utilidad en la práctica. Por lo que, en este punto resulta natural preguntarnos sobre cómo se comporta el producto de series de números complejos absolutamente convergentes. Para responder esta pregunta daremos dos resultados que consideran series convergentes y absolutamente convergentes.

Antes de continuar, recordemos el siguiente resultado de nuestros cursos de Cálculo.

Teorema 27.1. (Teorema de la convergencia monótona para sucesiones.)
Sea ${\left\{a_n\right\}}_{n\ge 0}\subset \mathbb{R}$ una sucesión real monótona. Entonces, ${\left\{a_n\right\}}_{n\ge 0}$ converge si y solo si es acotada.

Procedemos con los resultados mencionados previamente.

Proposición 27.7. (Producto de Cauchy absolutamente convergente.)
Sean $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ y $\sum _{n=0}^{\mathrm{\infty }}{w}_n$ dos series de números complejos absolutamente convergentes. Entonces, el producto de Cauchy de ambas series, es decir la serie $\sum _{n=0}^{\mathrm{\infty }}{c}_n$ dada en (27.2), es absolutamente convergente y se cumple que:
$$\sum _{n=0}^{\mathrm{\infty }}{c}_n=\left(\sum _{n=0}^{\mathrm{\infty }}{z}_n\right)\left(\sum _{n=0}^{\mathrm{\infty }}{w}_n\right).$$

Demostración. Dadas las hipótesis, primeramente procedemos a probar que la serie $\sum _{n=0}^{\mathrm{\infty }}{c}_n$, dada en (27.2), es absolutamente convergente.

Sean:
$$A=\sum _{n=0}^{\mathrm{\infty }}|z_n|,B=\sum _{n=0}^{\mathrm{\infty }}|w_n|,$$

y sea $s_n=\sum _{j=0}^n|c_j|$ la $n$-ésima suma parcial de la serie $\sum _{n=0}^{\mathrm{\infty }}|c_n|$.

De acuerdo con (27.1), para todo $j\in \mathbb{N}$ tenemos que:
$$c_j=\sum _{k=0}^j{z}_k{w}_{j-k}=z_0{w}_j+z_1{w}_{j-1}+\cdots +z_{j-1}{w}_1+z_j{w}_0.$$

Notemos que para todo $n\in \mathbb{N}$ se cumple que:
$$\begin{array}{rl}\sum _{j=0}^n{c}_j& =\sum _{j=0}^n\left(\sum _{k=0}^j{z}_k{w}_{j-k}\right)\\ & =\sum _{k=0}^0{z}_k{w}_{0-k}+\sum _{k=0}^1{z}_k{w}_{1-k}+\cdots +\sum _{k=0}^n{z}_k{w}_{n-k}\\ & =z_0{w}_0+(z_0{w}_1+z_1{w}_0)+\cdots +(z_0{w}_n+\cdots +z_n{w}_0)\\ & =\sum _{k=0}^n{z}_0{w}_k+\sum _{k=0}^{n-1}{z}_1{w}_k+\cdots +\sum _{k=0}^1{z}_{n-1}{w}_k+\sum _{k=0}^0{z}_n{w}_k\\ & =\sum _{j=0}^n\left(\sum _{k=0}^{n-j}{z}_j{w}_k\right).\end{array}$$

Es claro que se puede verificar esta igualdad por inducción, por lo que se deja como ejercicio al lector.

Por otra parte, para todo $n\in \mathbb{N}$ tenemos que:
$$s_{n+1}–s_n=\sum _{j=0}^{n+1}|c_j|–\sum _{j=0}^n|c_j|=|c_{n+1}|\ge 0,$$

de donde se sigue que la sucesión de sumas parciales ${\left\{s_n\right\}}_{n\ge 0}$, de la serie $\sum _{n=0}^{\mathrm{\infty }}|c_n|$, es creciente, es decir, es una sucesión monótona.

Considerando lo anterior, para todo $n\in \mathbb{N}$ tenemos que:
$$\begin{array}{r}{s}_n=\sum _{j=0}^n|c_j|=\sum _{j=0}^n\left|\sum _{k=0}^{n-j}{z}_j{w}_k\right|\le \sum _{j=0}^n\sum _{k=0}^{n-j}|z_j||w_k|\le \left(\sum _{j=0}^n|z_j|\right)\left(\sum _{k=0}^n|w_k|\right)\le AB.\end{array}$$

Entonces, la sucesión de sumas parciales ${\left\{s_n\right\}}_{n\ge 0}$, de la serie $\sum _{n=0}^{\mathrm{\infty }}|c_n|$, es acotada. Por lo que, de acuerdo con el teorema 27.1, la sucesión converge y por tanto la serie $\sum _{n=0}^{\mathrm{\infty }}{c}_n$ es absolutamente convergente.

Veamos ahora que la serie $\sum _{n=0}^{\mathrm{\infty }}{c}_n$ converge al producto de las series $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ y $\sum _{n=0}^{\mathrm{\infty }}{w}_n$.

De acuerdo con la proposición 27.3, tenemos que:
$$\begin{array}{rl}\left|\sum _{j=0}^n{c}_j–\sum _{j=0}^n{z}_j\sum _{k=0}^n{w}_k\right|& \le \left|\sum _{j=0}^n{z}_j\sum _{k=0}^{n-j}{w}_k–\sum _{j=0}^n{z}_j\sum _{k=0}^{\mathrm{\infty }}{w}_k\right|+\left|\sum _{j=0}^n{z}_j\sum _{k=0}^{\mathrm{\infty }}{w}_k–\sum _{j=0}^n{z}_j\sum _{k=0}^n{w}_k\right|\\ & =\left|\sum _{j=0}^n{z}_j\left(\sum _{k=0}^{\mathrm{\infty }}{w}_k–\sum _{k=0}^{n-j}{w}_k\right)\right|+\left|\sum _{j=0}^n{z}_j\left(\sum _{k=0}^{\mathrm{\infty }}{w}_k–\sum _{k=0}^n{w}_k\right)\right|\\ & =\left|\sum _{j=0}^n{z}_j\sum _{k=n-j+1}^{\mathrm{\infty }}{w}_k\right|+\left|\sum _{j=0}^n{z}_j\sum _{k=n+1}^{\mathrm{\infty }}{w}_k\right|\\ & \le \sum _{j=0}^n|z_j|\sum _{k=n-j+1}^{\mathrm{\infty }}|w_k|+\sum _{j=0}^n|z_j|\sum _{k=n+1}^{\mathrm{\infty }}|w_k|.\end{array}$$

Como las series $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ y $\sum _{n=0}^{\mathrm{\infty }}{w}_n$ son absolutamente convergentes, de acuerdo con el ejercicio 3 de esta entrada, al tomar límites tenemos que:
$$\underset{n\to \mathrm{\infty }}{lim}\left|\sum _{j=0}^n{c}_j–\sum _{j=0}^n{z}_j\sum _{k=0}^n{w}_k\right|=0,$$

entonces:
$$\underset{n\to \mathrm{\infty }}{lim}\left(\sum _{j=0}^n{c}_j–\sum _{j=0}^n{z}_j\sum _{k=0}^n{w}_k\right)=0,$$

de donde se sigue que:
$$\sum _{n=0}^{\mathrm{\infty }}{c}_n=\left(\sum _{n=0}^{\mathrm{\infty }}{z}_n\right)\left(\sum _{n=0}^{\mathrm{\infty }}{w}_n\right).$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Ejemplo 27.12.
En el ejemplo 27.11 vimos que la serie:
$$\sum _{n=0}^{\mathrm{\infty }}{c}_n=\sum _{n=0}^{\mathrm{\infty }}\frac{(z+w{)}^n}{n!},$$

es el producto de Cauchy de las series:
$$\sum _{n=0}^{\mathrm{\infty }}\frac{z^n}{n!}\text{y}\sum _{n=0}^{\mathrm{\infty }}\frac{w^n}{n!}.$$

Mientras que en el ejemplo 27.8 probamos que ambas series son absolutamente convergentes para todo $z,w\in \mathbb{C}$. Por lo que, de acuerdo con la proposición 27.7, concluimos que el producto de Cauchy de estas series es absolutamente convergente y es igual al producto de dichas series, es decir:
$$\left(\sum _{n=0}^{\mathrm{\infty }}\frac{z^n}{n!}\right)\left(\sum _{n=0}^{\mathrm{\infty }}\frac{w^n}{n!}\right)=\sum _{n=0}^{\mathrm{\infty }}\frac{(z+w{)}^n}{n!}.$$

Ejemplo 27.13.
Prueba que para $|z|<1$ se tiene que:
$$\sum _{n=0}^{\mathrm{\infty }}(n+1)z^n=\frac{1}{(1-z{)}^2}.$$

Solución.
Sabemos que la serie geométrica es convergente y se cumple que:
$$\sum _{n=0}^{\mathrm{\infty }}{z}^n=\frac{1}{1-z},\text{si}|z|<1.$$

Más aún, mediante el criterio de D’Alembert es fácil verificar que dicha serie es absolutamente convergente si $|z|<1$.

Entonces, por la proposición 27.7, tenemos que el producto de Cauchy de la serie geométrica consigo misma es absolutamente convergente y para $|z|<1$ se cumple que:
$$\begin{array}{rl}{\displaystyle \sum _{n=0}^{\mathrm{\infty }}{c}_n}& =\left({\displaystyle \sum _{n=0}^{\mathrm{\infty }}{z}^n}\right)\left({\displaystyle \sum _{n=0}^{\mathrm{\infty }}{z}^n}\right)\\ & =\left(\frac{1}{1-z}\right)\left(\frac{1}{1-z}\right)\\ & =\frac{1}{(1-z{)}^2}.\end{array}$$

Procedemos a obtener el producto de Cauchy. Sean $z_n=z^n=w_n$ para todo $n\in \mathbb{N}$, entonces:
$$\begin{array}{rl}\sum _{n=0}^{\mathrm{\infty }}{c}_n=\sum _{n=0}^{\mathrm{\infty }}\left(\sum _{k=0}^n{z}_k{w}_{n-k}\right)& =\sum _{n=0}^{\mathrm{\infty }}\left(\sum _{k=0}^n{z}^k{z}^{n-k}\right)\\ & =\sum _{n=0}^{\mathrm{\infty }}{z}^n\left(\sum _{k=0}^{n}1\right)\\ & =\sum _{n=0}^{\mathrm{\infty }}(n+1)z^n.\end{array}$$

Por lo tanto:
$$\sum _{n=0}^{\mathrm{\infty }}(n+1)z^n=\frac{1}{(1-z{)}^2},\text{si}|z|<1.$$

Proposición 27.8. (Teorema de Mertens sobre la convergencia del producto de Cauchy.)
Sean $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ y $\sum _{n=0}^{\mathrm{\infty }}{w}_n$ dos series de números complejos tales que una es absolutamente convergente y la otra es convergente. Entonces, el producto de Cauchy de ambas series, dado en (27.2), es convergente y se cumple que:
$$\sum _{n=0}^{\mathrm{\infty }}{c}_n=\left(\sum _{n=0}^{\mathrm{\infty }}{z}_n\right)\left(\sum _{n=0}^{\mathrm{\infty }}{w}_n\right).$$

Demostración. Dadas las hipótesis, sin pérdida de generalidad supongamos que $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ converge a $A\in \mathbb{C}$, $\sum _{n=0}^{\mathrm{\infty }}|z_n|=K\in \mathbb{R}$ y que $\sum _{n=0}^{\mathrm{\infty }}{w}_n$ converge a $B\in \mathbb{C}$.

Para todo $n\in \mathbb{N}$ definimos las sumas parciales de las series como:
$$s_n=\sum _{k=0}^n|z_k|,a_n=\sum _{k=0}^n{z}_k,b_n=\sum _{k=0}^n{w}_k,C_n=\sum _{k=0}^n{c}_k.$$

De acuerdo con (27.1), para todo $n\in \mathbb{N}$ se cumple que:
$$C_n=\sum _{j=0}^n{c}_j=\sum _{j=0}^n\left(\sum _{k=0}^j{z}_k{w}_{j-k}\right)=\sum _{j=0}^n\left(\sum _{k=0}^{n-j}{z}_j{w}_k\right)=\sum _{j=0}^n{z}_j\sum _{k=0}^{n-j}{w}_k.$$

Por lo que:
$$\begin{array}{rl}{C}_n=\sum _{j=0}^n{c}_j=\sum _{j=0}^n{z}_j{b}_{n-j}& =\sum _{j=0}^n{z}_j(B-(B-b_{n-j}))\\ & =\sum _{j=0}^n{z}_{j}B–\sum _{j=0}^n{z}_j(B-b_{n-j})\\ & =a_{n}B–\sum _{j=0}^n{z}_j(B-b_{n-j}).\end{array}$$

Dado que $\underset{n\to \mathrm{\infty }}{lim}{a}_{n}B=AB$, entonces solo resta probar que:
$$\underset{n\to \mathrm{\infty }}{lim}\sum _{j=0}^n{z}_j(B-b_{n-j})=0.$$

Sea $\epsilon >0$. Como $\underset{n\to \mathrm{\infty }}{lim}{b}_n=B$, entonces $\underset{n\to \mathrm{\infty }}{lim}(b_n–B)=0$. Por lo que, proposición 8.1, la sucesión ${\left\{b_n–B\right\}}_{n\ge 0}$ es acotada, es decir, existe $M>0$ tal que $|b_n-B|\le M$ para toda $n\in \mathbb{N}$.

Dado que la serie $\sum _{n=0}^{\mathrm{\infty }}|z_n|$ es convergente, para $\epsilon /2M>0$ tenemos que existe $N_1\in \mathbb{N}$ tal que si $n\ge N_1$, entonces:
$$\sum _{j=N_1+1}^{\mathrm{\infty }}|z_j|=\left|\sum _{j=0}^n|z_j|–\sum _{j=0}^{\mathrm{\infty }}|z_j|\right|<\frac{\epsilon }{2M}.$$

Supongamos que $\sum _{n=0}^{\mathrm{\infty }}|z_n|<\alpha$, con $\alpha >K\ge 0$. Como $\underset{n\to \mathrm{\infty }}{lim}{b}_n=B$, para $\epsilon /2\alpha >0$ tenemos que existe $N_2\in \mathbb{N}$ tal que si $n\ge N_2$, entonces:
$$\left|b_n–B\right|<\frac{\epsilon }{2\alpha }.$$

Sea $N\ge N_1+N_2$. Notemos que para $j\le N_1$, se cumple que $N–j\ge N_2$. Entonces, para toda $n\ge N$ tenemos que:
$$\begin{array}{rl}|\sum _{j=0}^n{z}_j(B-b_{n-j})|& =|\sum _{j=0}^{N_1}{z}_j(B-b_{n-j})+\sum _{j=N_1+1}^n{z}_j(B-b_{n-j})|\\ & \le \sum _{j=0}^{N_1}|z_j||B-b_{n-j}|+\sum _{j=N_1+1}^n|z_j||B-b_{n-j}|\\ & \le \frac{\epsilon }{2\alpha }\sum _{j=0}^{N_1}|z_j|+M\sum _{j=N_1+1}^n|z_j|\\ & <\left(\frac{\epsilon }{2\alpha }\right)\alpha +M\left(\frac{\epsilon }{2M}\right)\\ & =\epsilon .\end{array}$$

Entonces:
$$\underset{n\to \mathrm{\infty }}{lim}{C}_n=\underset{n\to \mathrm{\infty }}{lim}\sum _{j=0}^n{c}_j=\underset{n\to \mathrm{\infty }}{lim}(a_{n}B–\sum _{j=0}^n{z}_j(B-b_{n-j}))=AB,$$

de donde se sigue que el producto de Cauchy de las series es convergente y se cumple que:
$$\sum _{n=0}^{\mathrm{\infty }}{c}_n=\left(\sum _{n=0}^{\mathrm{\infty }}{z}_n\right)\left(\sum _{n=0}^{\mathrm{\infty }}{w}_n\right).$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Definición 27.6. (Sucesiones y series doblemente infinitas.)
Una sucesión de números complejos doblemente infinita es una función $f:\mathbb{Z}\to \mathbb{C}$ tal que a cada $n\in \mathbb{Z}$ asigna de manera única un número complejo. Si $f(n)=z_n\in \mathbb{C}$ para todo $n\in \mathbb{Z}$, entonces denotamos a la sucesión de números complejos doblemente infinita como ${\left\{z_n\right\}}_{n\in \mathbb{Z}}$ ó ${\left\{z_n\right\}}_{n=-\mathrm{\infty }}^{\mathrm{\infty }}$.

Una serie de números complejos doblemente infinita es una expresión de la forma:
$$\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{z}_n.$$

Definición 27.7. (Sumas parciales de una serie doblemente infinita.)
Dada una serie de números complejos doblemente infinita $\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{z}_n$, para cada par de números $n,m\in {\mathbb{N}}^{+}$ definimos la sucesión de sumas parciales de la serie como:
$$s_{m,n}=\sum _{k=-m}^n{z}_k=z_{-m}+z_{-m+1}+\cdots +z_{n-1}+z_n.$$

Definición 27.8. (Serie doblemente infinita convergente.)
Diremos que una serie de números complejos doblemente infinita $\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{z}_n$ converge a $s\in \mathbb{C}$ si $s_{m,n}\to s$ conforme $m\to \mathrm{\infty }$ y $n\to \mathrm{\infty }$ de forma independiente, es decir, si para todo $\epsilon >0$ existe $N(\epsilon )\in {\mathbb{N}}^{+}$ tal que si $m\ge N$ y $n\ge N$, entonces:
$$|s_{m,n}–s|=\left|\sum _{k=-m}^n{z}_k–s\right|<\epsilon .$$

En tal caso, denotaremos la convergencia de la serie a $s$ como $s=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{z}_n$. En caso de no existir $s\in \mathbb{C}$ con tal propiedad, diremos que la serie de números complejos doblemente infinita es divergente.

Lema 27.1.
Una serie de números complejos doblemente infinita $\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{z}_n$ converge a $s=s^{-}+s^{+}\in \mathbb{C}$ si y solo si las series de números complejos $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ y $\sum _{n=1}^{\mathrm{\infty }}{z}_{-n}$ convergen a $s^{+}$ y $s^{-}$, respectivamente. En tal caso:
$$\begin{array}{}\text{(27.3)}& \sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{z}_n=\sum _{n=1}^{\mathrm{\infty }}{z}_{-n}+\sum _{n=0}^{\mathrm{\infty }}{z}_n.\end{array}$$

Demostración.
Sean $m\ge 1$ y $n\ge 1$, entonces las sucesiones de sumas parciales de cada serie están dadas por:
$$s_{m,n}=\sum _{k=-m}^n{z}_k=z_{-m}+z_{-m+1}+\cdots +z_{n-1}+z_n,$$
$$s_{-m}=\sum _{k=-m}^{-1}{z}_k=z_{-m}+z_{-m+1}+\cdots +z_{-2}+z_{-1},$$
$$s_n=\sum _{k=0}^n{z}_k=z_0+z_1+\cdots +z_{n-1}+z_n,$$ de donde $s_{m,n}=s_{-m}+s_n$.

$(⟸$

Supongamos que $s^{-}=\sum _{n=1}^{\mathrm{\infty }}{z}_{-n}$ y $s^{+}=\sum _{n=0}^{\mathrm{\infty }}{z}_n$, con $s^{-},s^{+}\in \mathbb{C}$, es decir que ambas series son convergentes.

Entonces, por la proposición 27.2 es claro que si $m\to \mathrm{\infty }$ y $n\to \mathrm{\infty }$ entonces $s_{m,n}=s_{-m}+s_n\to s^{-}+s^{+}$, por lo que la serie $\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{z}_n$ converge y se cumple (29.3).

$⟹)$

Supongamos que la serie $\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{z}_n$ converge a $s\in \mathbb{C}$.

Probaremos que la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ converge utilizando el criterio de Cauchy. La convergencia de la serie restante es análoga y se deja como ejercicio al lector.

Sea $\epsilon >0$. De acuerdo con la definición 27.7 tenemos que existe $M\in {\mathbb{N}}^{+}$ tal que si $p\ge M$ y $q\ge M$, con $p,q\in {\mathbb{N}}^{+}$, entonces $|s_{p,q}–s|<\epsilon /2$. En particular $|s_{M,q}–s|<\epsilon /2$ si $q\ge M$. Sea $N=M+1$, entonces para $n,m\ge N$, con $n>m$, por la desigualdad del triángulo tenemos que:
$$\left|\sum _{k=m+1}^n{z}_k\right|=|s_{M,n}–s_{M,m}|\le |s_{M,n}–s|+|s–s_{M,m}|<\frac{\epsilon }{2}+\frac{\epsilon }{2}=\epsilon .$$

Por lo que, de acuerdo con la proposición 27.1, tenemos que la serie $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ converge.

De acuerdo con la primera parte de la prueba, como las series $\sum _{n=1}^{\mathrm{\infty }}{z}_{-n}$ y $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ convergen, entonces se cumple (27.3).

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Observación 27.6.
De acuerdo con el lema anterior, es común definir la convergencia de una serie de números complejos doblemente infinita $\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{z}_n$, en función de la convergencia de las series $\sum _{n=1}^{\mathrm{\infty }}{z}_{-n}$ y $\sum _{n=0}^{\mathrm{\infty }}{z}_n$, en cuyo caso se dice que la serie doblemente infinita converge a la suma de ambas series dada en (27.3).

Ejemplo 27.14.
Analicemos el comportamiento de la serie $\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{2}^{-|n|}{z}^n$.

Solución. De acuerdo con el lema 27.1, podemos analizar la convergencia de la serie doblemente infinita al separarla en dos series, dadas por $n\ge 0$ y $n<0$.

Para $n\ge 0$ tenemos que:
$$\sum _{n=0}^{\mathrm{\infty }}{2}^{-|n|}{z}^n=\sum _{n=0}^{\mathrm{\infty }}\frac{z^n}{2^{|n|}}=\sum _{n=0}^{\mathrm{\infty }}{\left(\frac{z}{2}\right)}^n=\frac{1}{1-{\displaystyle \frac{z}{2}}}=\frac{2}{2-z},$$ si $|z/2|<1$, es decir si $|z|<2$. Mientras que la serie diverge si $|z|\ge 2$.

Por otra parte, para $n<0$ tenemos que:
$$\begin{array}{rl}\sum _{n=-\mathrm{\infty }}^{-1}{2}^{-|n|}{z}^n=\sum _{n=1}^{\mathrm{\infty }}{2}^{-|-n|}{z}^{-n}=\sum _{n=1}^{\mathrm{\infty }}\frac{1}{z^n{2}^{|n|}}& =\sum _{n=1}^{\mathrm{\infty }}{\left(\frac{1}{2z}\right)}^n\\ & =\left(\frac{1}{2z}\right)\sum _{n=1}^{\mathrm{\infty }}{\left(\frac{1}{2z}\right)}^{n-1}\\ & =\left(\frac{1}{2z}\right)\sum _{k=0}^{\mathrm{\infty }}{\left(\frac{1}{2z}\right)}^k\\ & =\left(\frac{1}{2z}\right)\left(\frac{1}{1-{\displaystyle \frac{1}{2z}}}\right)\\ & =\frac{1}{2z-1},\end{array}$$ si se cumple que $|1/(2z)|<1$, es decir si $|z|>1/2$. Mientras que la serie diverge en otro caso.

Entonces, de acuerdo con el lema 27.1, para los $z\in \mathbb{C}$ tales que $1/2<|z|<2$, tenemos que la serie converge y en tal caso:
$$\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{2}^{-|n|}{z}^n=\frac{2}{2-z}+\frac{1}{2z-1}=\frac{3z}{(2-z)(2z-1)}.$$

Podemos visualizar la región de convergencia y los valores que toma la serie en el siguiente Applet de GeoGebra: https://www.geogebra.org/m/eqjzzthz.

Tarea moral

1. Completa la demostración de la proposición 27.2.
2. Prueba el corolario 27.4.
3. Prueba que si una serie ${\displaystyle \sum _{n=0}^{\mathrm{\infty }}{z}_n}$ converge, entonces $\underset{m\to \mathrm{\infty }}{lim}{\displaystyle \sum _{n=m+1}^{\mathrm{\infty }}{z}_n=0}$, es decir, si la serie converge entonces su cola tiende a $0$.
4. Muestra que:
   a) ${\displaystyle \sum _{n=0}^{\mathrm{\infty }}{\displaystyle \frac{1}{(2+i{)}^n}}={\displaystyle \frac{3-i}{2}}}$.
   b) ${\displaystyle \sum _{n=0}^{\mathrm{\infty }}\left({\displaystyle \frac{1}{n+1+i}}–{\displaystyle \frac{1}{n+i}}\right)=i}$.
   c) ${\displaystyle \sum _{n=0}^{\mathrm{\infty }}{\displaystyle \frac{(1+i{)}^n}{2^n}}=1+i}$.
   d) ${\displaystyle \sum _{n=0}^{\mathrm{\infty }}{\displaystyle \frac{(1-i{)}^n}{2^n}}=1-i}$.
5. Prueba que las siguientes series convergen.
   a) ${\displaystyle \sum _{n=1}^{\mathrm{\infty }}{\displaystyle \frac{(3+4i{)}^n}{5^n{n}^2}}}$.
   b) ${\displaystyle \sum _{n=1}^{\mathrm{\infty }}\left({\displaystyle \frac{1}{n+2i}}–{\displaystyle \frac{1}{n+1+2i}}\right)}$.
   c) ${\displaystyle \sum _{n=1}^{\mathrm{\infty }}{\displaystyle \frac{i}{n(n+1)}}}$.
   d) ${\displaystyle \sum _{n=0}^{\mathrm{\infty }}{\displaystyle \frac{(1+i{)}^{2n}}{(2n+1)!}}}$.
6. Utiliza la serie geométrica para determinar la mayor región de convergencia de las siguientes series y obtén el valor de cada suma.
   a) ${\displaystyle \sum _{n=0}^{\mathrm{\infty }}[{\left({\displaystyle \frac{2}{z}}\right)}^n+{\left({\displaystyle \frac{z}{3}}\right)}^n]}$.
   b) ${\displaystyle \sum _{n=0}^{\mathrm{\infty }}{\left({\displaystyle \frac{(3+i)z}{4-i}}\right)}^n}$.
   c) ${\displaystyle \sum _{n=1}^{\mathrm{\infty }}{(1+z)}^n}$.
   d) ${\displaystyle \sum _{n=0}^{\mathrm{\infty }}{\displaystyle \frac{2^{n+1}}{(2+i-z{)}^n}}}$.
7. Sean $r,\theta \in \mathbb{R}$, con $0\le r<1$. Muestra que:
   a) ${\displaystyle \sum _{n=0}^{\mathrm{\infty }}{r}^n{e}^{in\theta }={\displaystyle \frac{1}{1-r{e}^{i\theta }}}}$.
   b) ${\displaystyle \sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{r}^{|n|}{e}^{in\theta }={\displaystyle \frac{1}{1-r{e}^{-i\theta }}}+{\displaystyle \frac{r{e}^{i\theta }}{1-r{e}^{i\theta }}}}$.
   c) ${\displaystyle \sum _{n=0}^{\mathrm{\infty }}{r}^n\cos (n\theta )={\displaystyle \frac{1-r\cos (\theta )}{1+r^2-2r\cos (\theta )}}}$.
   d) ${\displaystyle \sum _{n=0}^{\mathrm{\infty }}{r}^n\mathrm{sen}(n\theta )={\displaystyle \frac{r\mathrm{sen}(\theta )}{1+r^2-2r\cos (\theta )}}}$.
8. Sean $\sum _{n=0}^{\mathrm{\infty }}{z}_n$ y $\sum _{n=0}^{\mathrm{\infty }}{z}_n^2$ dos series convergentes, de números complejos tales que $\mathrm{Re}(z_n)\ge 0$, para todo $n\in \mathbb{N}$. Prueba que la serie $\sum _{n=0}^{\mathrm{\infty }}|z_n{|}^2$ es convergente.
9. Muestra que: $${\displaystyle \sum _{n=1}^{\mathrm{\infty }}\frac{n(n+1)}{2}{z}^{n-1}=\frac{1}{(1-z{)}^3}.}$$ Hint: Considera el resultado del ejemplo 27.13 y utiliza la identidad ${\displaystyle \sum _{k=1}^{n}k={\displaystyle \frac{n(n+1)}{2}}}$.
10. Determina para qué valores de $z\in \mathbb{C}$ la serie ${\displaystyle \sum _{n=0}^{\mathrm{\infty }}{e}^{inz}}$ converge, es decir, su región de convergencia.
    Hint: Considera la serie geométrica.

Más adelante…

En esta entrada hemos dado la definición de serie, desde el sentido complejo, y probamos algunos resultados elementales para estudiar la convergencia de una serie, los cuales nos serán de utilidad en las siguientes entradas.

Al igual que con muchos otros conceptos, las definiciones y criterios obtenidos para las series de números complejos son muy similares a los que estudiamos en nuestros cursos de Cálculo para las series de números reales.

La siguiente entrada abordaremos los conceptos de sucesión y serie de funciones complejas, así como los conceptos de convergencia puntual y uniforme. Además de obtener algunos resultados elementales en el estudio de las series de funciones complejas.

Entradas relacionadas

• Ir a Variable Compleja I.
• Entrada anterior del curso: Funciones complejas como transformaciones. Técnicas de graficación.
• Siguiente entrada del curso: Sucesiones y series de funciones.