Un problema de saltamontes en cuarentena

Nota de Leo: Esta es una entrada invitada de Adán Medrano Martín del Campo. Nos platicará de un problema de saltamontes (de hecho, de dos) y de funciones en los enteros.

$\text{Tu}\in \text{Casa}$

Esto nos aconsejó muy atinadamente el Dr. Hugo López-Gatell Ramírez hace unos pocos días, ya que México y la mayoría del mundo está en cuarentena a causa de la enfermedad COVID19.

Cada vez más y más personas buscamos nuevas actividades para hacer en casa. Junto con Leo Martínez, David Torres (aka Gato) y Pablo Meré, administro el grupo de facebook InsOMMnia, el cual sirve de plataforma para discutir y realizar actividades olímpicamente productivas. A modo de amenizar la cuarentena, hice un video en vivo explicando la solución a un problema que me pareció particularmente agradable por varias razones:

Apareció en el examen de selección del equipo rumano de la IMO 2019
Es parecido al problema 5 de la OMM 2019
Es, en cierto sentido, un problema de saltamontes

En esta entrada, quisiera platicarles el problema y su solución. Antes de esto, recordemos el problema que apareció en la OMM 2019.

La Momia: OMM 2019

Problema 5. Sean $a>b$ dos números enteros positivos, primos relativos entre sí. En un camino recto, en el cual está marcado cada centímetro $n$ , para todo entero $n$ , un saltamontes hará algunos saltos comenzando en la marca de $0$ cm y siguiendo las siguientes reglas:

Cuando cierto minuto sea múltiplo de $a$ y no múltiplo de $b$ , saltará $a$ centímetros hacia adelante.
Cuando cierto minuto sea múltiplo de $b$ y no múltiplo de $a$ , saltará $b$ centímetros hacia atrás.
Cuando cierto minuto sea múltiplo de $a$ y múltiplo de $b$ , saltará $a-b$ centímetros hacia adelante.
Cuando un minuto no es múltiplo de $a$ ni de $b$ , el saltamontes no se mueve del lugar en el que está.

Determina todas las marcas a las que puede llegar el saltamontes.

Nota de Leo: Este es un excelente problema para explorarse buscando un patrón.

Sin dar un spoiler de la solución a dicho problema, el enunciado puede traducirse al siguiente problema de equivalente.

Problema 5′: Sean $a>b$ enteros primos positivos primos relativos entre sí y sea $f:\mathbb{N}\to\mathbb{Z}$ la función dada por

$f(n)=a\left\lfloor\frac{n}{a}\right\rfloor-b\left\lfloor\frac{n}{b}\right\rfloor.$

Determina la imagen de $f$ .

Uno puede jugar un poco con la función definida arriba, y llegar a la respuesta usando propiedades de dicha función. El objetivo de mostrarles este enunciado equivalente, es que muchas veces ciertos problemas que hablan de ciertos procesos pueden describirse (y resolverse) en términos de funciones construidas apropiadamente.

El problema que resolveremos cae en la categoría opuesta, pues es un problema sobre una función, al cual se le puede dar una interpretación de un saltamontes haciendo… algo.

El Vampiro: Romania TST 2019

Problema: Sean $a<b<c$ enteros positivos y sea $f:\mathbb{N}\to \mathbb{N}$ una función dada por

$f(n)=\begin{cases}n-a & n>c \\f(f(n+b)) & n\leq c\end{cases}$

Determina la cantidad de enteros positivos $n$ tales que $f(n)=n$ .

«Y eso qué tiene que ver con un saltamontes?» podrías pensar en este momento. ¡Ha ha! Mira ahora este problema de saltamontes.

Problema’: Sean $a<b<c$ enteros positivos. Un saltamontes se encuentra sobre un entero $n>0$ en la recta real positiva, donde hay pasto en los enteros positivos menores o iguales que $c$ , y lava en los enteros mayores a $c$ . Inicialmente, el saltamontes tiene una vida, y mientras el saltamontes tenga al menos una vida, se dispondrá a saltar de la siguiente manera:

Si el saltamontes se encuentra en el pasto, el saltamontes gana una vida y salta $b$ enteros hacia adelante.
Si el saltamontes se encuentra en la lava, el saltamontes pierde una vida y salta $a$ enteros hacia atrás.

Cuando el saltamontes tiene $0$ vidas, este muere y deja de moverse. Determina todas las posiciones iniciales del saltamontes tal que el saltamontes morirá en su posición inicial.

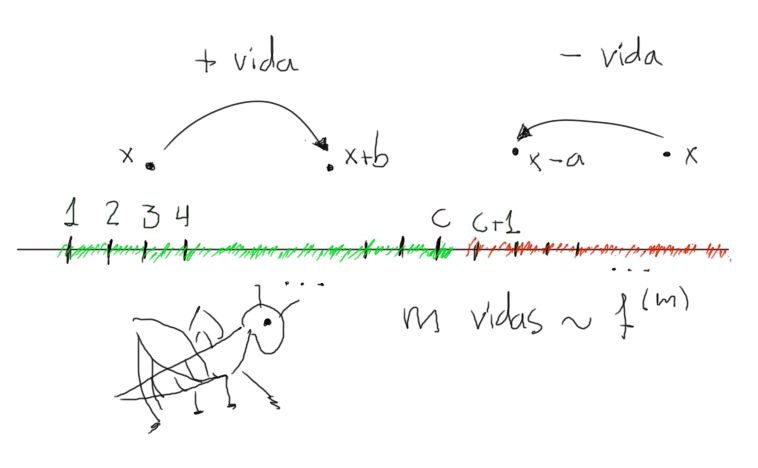
Saltamontes, lava, pasto y vidas — Problema visto como vidas, pasto, lava y saltamontes.

A que no se lo esperaban. (Honestamente yo tampoco, pero últimamente tengo más tiempo libre). Tal vez este problema inspire algún mini juego en alguna entrega futura de The Legend of Zelda.

Y, ¿cómo resolvemos algo así?

El Santo: venciendo a la momia y al vampiro

Spoiler Alert:

A continuación resolveremos los problemas, en caso que estés intentándolos y no quieras ver sus soluciones

La clave para ambos problemas es: ¡usar residuos y propiedades de las funciones en juego!

Solución al problema 5 del nacional

Notemos que al dividir $n$ entre $a$ y entre $b$ , obtenemos

$n=a\left\lfloor \frac{n}{a}\right\rfloor+r_{a}$

$n=b\left\lfloor \frac{n}{b}\right\rfloor+r_{b}$

donde

$0\leq r_{a}\leq a-1$

$0\leq r_{b}\leq b-1$

son precisamente los residuos que resultan de la división. Notemos entonces que

$\begin{align*}f(n)&=a\left\lfloor\frac{n}{a}\right\rfloor-b\left\lfloor\frac{n}{b}\right\rfloor\\&=\left(n-b\left\lfloor \frac{n}{b}\right\rfloor\right)-\left(n-a\left\lfloor \frac{n}{a}\right\rfloor\right)\\&=r_{b}-r_{a}\end{align*}$

por lo que $f(n)$ simplemente depende de la diferencia entre $r_{b}$ y $r_{a}$ . Por el Teorema Chino del Residuo, o simplemente mirando exclusivamente a los múltiplos de $a$ y de $b$ entre $1$ y $ab$ , aparecen como diferencia todos los posibles enteros en el intervalo

$[-a+1, b-1]$

lo cual compone la imagen de $f$ , que es lo que buscábamos.

$\square$

¡Genial! Mirar los residuos fue clave en el problema de saltamontes del nacional. En particular, no lo usamos en nuestra solución, pero $f$ resulta ser una función periódica, con periodo $ab$ . Esto es gracias a que $a$ y $b$ son primos relativos, y por lo tanto cada pareja de residuos $r_{a}, r_{b}$ se repiten exactamente cada $ab$ enteros.

La periodicidad será una propiedad clave en la solución del problema del selectivo rumano. Comenzamos mostrando una exploración del problema.

Exploración del problema del selectivo rumano

Los puntos $n$ tales que $f(n)=n$ son llamados puntos fijos. En la formulación como problema de saltamontes, corresponden a que el saltamontes muera justo donde empezó: «muera» es que ya no haya $f$ , empieza con una vida, osea una $f$ .

Notemos que si $n>c$ , entonces $n$ no es un punto fijo, pues

$f(n)=n-a\neq n.$

Esto nos dice que los puntos fijos son menores o iguales que $c$ . Ahora, notemos que (recordemos que $a<b<c$ )

$\begin{align*}f(c)&=f(f(c+b))\\&=f(c+b-a)=c+b-2a\end{align*}$

y esto nos lleva a considerar que números cercanos a $c$ , dentro de un intervalo de tamaño $b-a$ , tendrán un valor similar. En efecto, si $0\leq r<b-a$ entonces

$\begin{align*}f(c-r)&=f(f(c-r+b))\\&=f(c-r+b-a)\\&=c-r+b-2a.\end{align*}$

Ahora, veamos que restando $b-a$ a $c$ , perdemos este patrón, pues

$\begin{align*}f(c-b+a)&=f(f(c+a))\\&=f(c)\\&=c+b-2a\end{align*}$

¡Hemos regresado a un valor ya conocido! Esto nos lleva a la hipótesis de que $f$ es periódica con periodo $b-a$ en el intervalo $[1, c]$ . Formalicemos estas observaciones.

Un par de lemas para el problema rumano

La manera de enunciar formalmente las observaciones anteriores esto es, por ejemplo, via el siguiente lema:

Lema 1: Sea $n=c-r-k(b-a)$ un entero positivo menor o igual que $c$ donde $k\geq 0$ y $0\leq r<b-a$ . Entonces

$f(n)=c-r+b-2a.$

(Prueba del lema 1): Procederemos por descenso en los enteros positivos. Construiremos una secuencia de valores iguales, con distinta cantidad de $f$ ‘s compuestas, de la siguiente manera: comenzamos con

$z_{0}=n=c-r-k(b-a)$

y definimos

$z_{i+1}=\begin{cases}z_{i}-a & z_{i}>c \\z_{i}+b & z_{i}\leq c\end{cases}$

para todo $i\geq 0$ . Además, escribiremos

$z_{i}=c-r-y_{i}b+x_{i}a$

donde $x_{0}=y_{0}=k$ , y ambas secuencias $\left\{x_{i}\right\}$ y $\left\{y_{i}\right\}$ decrecen, definiendo

$x_{i+1}=\begin{cases}x_{i}-1 & z_{i}>c \\x_{i} & z_{i}\leq c\end{cases}$

$y_{i+1}=\begin{cases}y_{i} & z_{i}>c \\y_{i}-1 & z_{i}\leq c\end{cases}$

Habiendo definido esto, tenemos que

$f(n)=f^{(1+x_{i}-y_{i})}(z_{i})$

para todo $i\geq 0$ .

Observemos que si $y_{i}=-1$ entonces $z_{i}=c-r+b+x_{i}a>c$ si se cumple que $x_{i}\geq -1$ . Más aún, observemos el siguiente lema:

Lema 2: Para todo $i\geq 0$ , tenemos que $y_{i}\geq 0$ implica que $y_{i+1}\leq x_{i+1}$ .

(Prueba del lema 2): Procedemos por inducción. Para $i=0$ esto es claro, pues

$y_{1}=k-1<k=x_{1}.$

Ahora, supongamos que $x_{i}\geq y_{i}\geq 0$ . Si $x_{i}>y_{i}$ entonces

$x_{i+1}\geq x_{i}-1\geq y_{i}\geq y_{i+1}.$

Si $x_{i}=y_{i}$ entonces tenemos que

$z_{i}=c-r-y_{i}(b-a)\leq c$

por lo que $z_{i+1}=z_{i}+b$ y esto implica que

$x_{i+1}=x_{i}>y_{i}-1=y_{i+1}.$

$\square$

Hemos probado pues que las secuencias $\left\{x_{i}\right\}$ y $\left\{y_{i}\right\}$ decrecen, y mientras $y_{i}\geq 0$ , tendremos que $x_{i+1}\geq y_{i+1}$ . ¿Cómo hemos de proseguir con esto?

La clave es notar la existencia de la menor $m$ tal que $y_{m}=-1$ , donde es claro que $y_{m-1}=0$ . Si $m=1$ entonces $y_{0}=x_{0}=k=0$ , y ya hemos cubierto ese caso arriba, así que asumiremos que $m>1$ . Tenemos que $y_{m-2}\geq 0$ por lo que, por el lema 2,

$x_{m-1}\geq y_{m-1}=0$

y como $y_{m}=y_{m-1}-1$ entonces $x_{m}=x_{m-1}\geq 0$ . Esto implica que

$\begin{align*}z_{m}&=c-r+b+x_{m}a\\&\geq c-r+b\\&>c\end{align*}$

por lo que para todo $j>m$ se tiene que $x_{j+1}=x_{j}-1$

$z_{m+x_{m}+1}=c-r+b-a$

y tenemos que $y_{m+x_{m}+1}=x_{m+x_{m}+1}=-1$ , lo que muestra que

$\begin{align*}f(n)&=f(z_{m+x_{m}+1})\\&=f(c-r+b-a)\\&=c-r+b-2a.\end{align*}$

$\square$

Juntando todo

Vaya, después de arduo trabajo hemos mostrado la periodicidad de $f$ . Lo que falta únicamente, es usar esto para hacer una conclusión sobre los puntos fijos. Notemos que los únicos valores de $f$ en el dominio $[1, c]$ son $c-r+b-2a$ para $0\leq r<b-a$ , así que solo estos valores pueden ser puntos fijos de $f$ . De hecho, cada uno de esos valores es un punto fijo si y solo si podemos encontrar una $k\geq 0$ tal que

$c-r-k(b-a)=c-r+b-2a$

, lo cual sucede si y sólo si $(k+1)(b-a)=a$ , o bien justo cuando $b-a\mid a$ , por lo que si $b-a$ divide a $a$ , todos nuestros $b-a$ valores son puntos fijos, y si $b-a$ no divide a $a$ , ningún valor es un punto fijo. Hemos concluido entonces.

$\square$

Antes de regresar a la cuarentena

Espero que hayan pasado un rato agradable pensando en este problema, y espero que hayan entendido 4 lecciones:

Quédate en casa
Quédate en casa
Quédate en casa
Es una buena idea usar residuos y secuencias jugando con enteros.

Con esto me despido y, ¡hasta la próxima!

El blog de Leo

Aprendiendo, creando y compartiendo matemáticas

Un problema de saltamontes en cuarentena

La Momia: OMM 2019

El Vampiro: Romania TST 2019

El Santo: venciendo a la momia y al vampiro

Solución al problema 5 del nacional

Exploración del problema del selectivo rumano

Un par de lemas para el problema rumano

Juntando todo

Antes de regresar a la cuarentena

Deja una respuesta Cancelar la respuesta

La Momia: OMM 2019

El Vampiro: Romania TST 2019

El Santo: venciendo a la momia y al vampiro

Solución al problema 5 del nacional

Exploración del problema del selectivo rumano

Un par de lemas para el problema rumano

Juntando todo

Antes de regresar a la cuarentena

Comparte esto:

Deja una respuesta Cancelar la respuesta