Introducción

Uno de los teoremas clave de los cursos de cálculo de varias variables es el teorema de la función inversa (TFI). En la Facultad de Ciencias de la UNAM se estudia en la materia Cálculo III. En esta entrada me gustaría presentar de la manera más auto-contenida posible este resultado.

Platicaré un poco de las definiciones de los términos que aparecen en el enunciado, así como de la intuición de por qué el teorema es cierto. Después presentaré los ingredientes principales para una prueba. Finalmente, presentaré la prueba intentando motivarla y dividiéndola en secciones pequeñas.

El enunciado con el que trabajaremos es el siguiente:

Teorema de la función inversa. Sea $F:{\mathbb{R}}^n\to {\mathbb{R}}^n$ una función de clase ${\mathcal{C}}^1$ con matriz Jacobiana $DF$. Supongamos que $F(a)=b$ y que $DF(a)$ es invertible. Entonces existen vecindades abiertas $U$ y $V$ de $a$ y $b$ respectivamente para las cuales:

a) $F:U\to V$ es una biyección,
b) su inversa $F^{-1}:V\to U$ es de clase ${\mathcal{C}}^1$ y
c) $D{F}^{-1}(b)=DF(a{)}^{-1}$.

Lo que nos espera es aproximadamente lo que está en el siguiente diagrama, donde las flechas indican a grandes rasgos qué resultado se usa para probar qué otro.

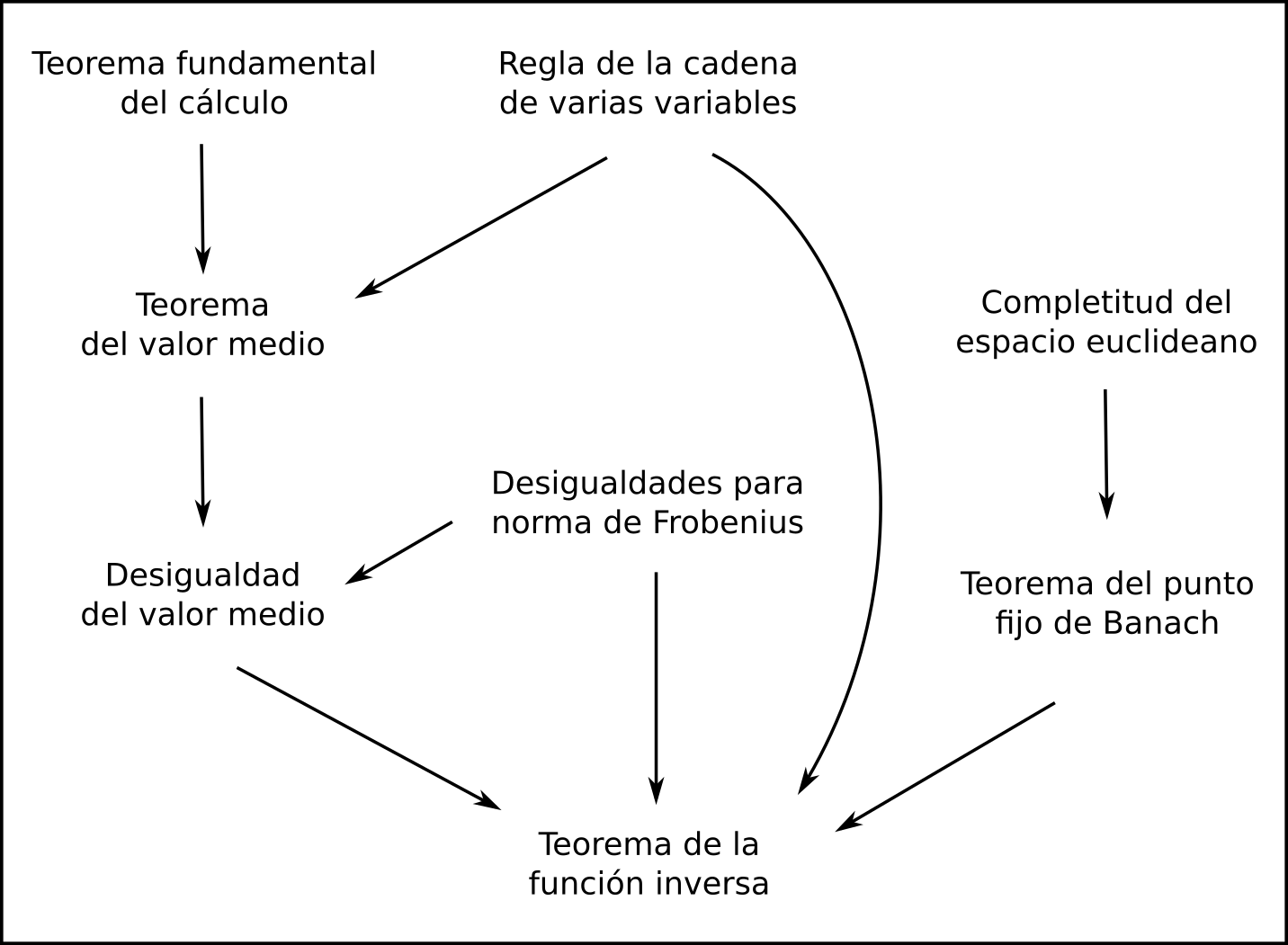
Definiciones e intuición

La función con la que comenzamos es una función de ${\mathbb{R}}^n$ a ${\mathbb{R}}^n$, así que la podemos descomponer en sus funciones coordenadas de la siguiente manera: $$F(x)=(F_1(x),F_2(x),\dots ,F_n(x)).$$

Que la función sea de clase ${\mathcal{C}}^1$ quiere decir que las derivadas parciales con respecto a cada una de las variables existen, que estas son continuas y que localmente $F$ «se comporta» como la transformación lineal correspondiente a la matriz Jacobiana siguiente:

$$DF(x)=\left(\begin{array}{ccc}\frac{\partial F_1}{\partial x_1}(x)& \cdots & \frac{\partial F_1}{\partial x_n}(x)\\ ⋮& \ddots & ⋮\\ \frac{\partial F_n}{\partial x_1}(x)& \cdots & \frac{\partial F_n}{\partial x_n}(x)\end{array}\right).$$

Entonces, a grandes rasgos lo que nos dice el teorema de la función inversa es lo siguiente. Si $F$ se comporta como una transformación lineal $T$ invertible «cerquita» del punto $a$, entonces en realidad es invertible «cerquita» del punto $a$ y más aún, la inversa se comporta como la transformación lineal $T^{-1}$ «cerquita» del punto $b=f(a)$.

Suena bastante razonable, pero hay algunos aspectos que son sorprendentes. Uno es que se garantiza la invertibilidad en todo un abierto $U$. Si no se requiriera que fuera abierto, sería chafa porque podríamos tomar $U=\{a\}$ y $V=\{b\}$ y la restricción sería trivialmente invertible. Lo otro es que el teorema también garantiza que la inversa es diferenciable, lo cual de entrada no es evidente.

Para la prueba necesitamos hablar de dos normas. Cuando tengamos un vector $x=(x_1,\dots ,x_n)$ en ${\mathbb{R}}^n$, $\Vert x\Vert$ denotará la norma euclideana $$\Vert x\Vert =\sqrt{\sum _{i=1}^n{x}_i^2}.$$

Necesitaremos también la norma de Frobenius. Como recordatorio, para una matriz $A=(a_{ij})$ de $n\times n$, su norma de Frobenius está dada por $$\Vert A\Vert =\sqrt{\sum _{i=1}^n\sum _{j=1}^n{a}_{ij}^2},$$

o equivalentemente, si $A_i$ es el $i$-ésimo renglón de $A$, tenemos que

$$\Vert A\Vert =\sqrt{\sum _{i=1}^n{\Vert A_i\Vert }^2},$$

pues ambas expresiones suman todas las entradas de la matriz al cuadrado.

Ingredientes para la prueba

Pasemos ahora a algunos resultados auxiliares que es más cómodo probar desde antes. Algunos de ellos son más generales que lo que enuncio (e incluso con la misma prueba), pero con el fin de que la demostración sea auto-contenida, he decidido enunciar sólo lo que necesitamos.

Teorema del punto fijo de Banach (para ${\mathbb{R}}^n$). Sea $X$ un compacto de ${\mathbb{R}}^n$ y $\phi :X\to X$ una función continua. Supongamos que $\phi$ es una contracción, es decir, que existe un real $0<\lambda <1$ para el cual $\Vert \phi (x)-\phi (y)\Vert \le \lambda \Vert x-y\Vert$ para todos $x,y\in X$.

Entonces $\phi$ tiene un único punto fijo, es decir existe uno y sólo un punto $x_0\in X$ para el cual $\phi (x_0)=x_0$.

Para probar el teorema del punto fijo de Banach basta tomar cualquier punto inicial $x_1$ y considerar la sucesión $\{x_m\}$ construida recursivamente con la regla $x_m=\phi (x_{m-1})$ para $m\ge 2$. Usando que $\phi$ es contracción y la fórmula para series geométricas se puede mostrar inductivamente que para $m>m^{\prime }$ se tiene

$$\Vert x_m-x_m^{\prime }\Vert \le {\lambda }^{m^{\prime }-1}\Vert x_2-x_1\Vert \left(\frac{1}{1-\lambda }\right).$$

Como $\lambda <1$, el lado derecho se hace arbitrariamente pequeño conforme $m^{\prime }$ se hace grande, así que ésta es una sucesión de Cauchy. Por la compacidad de $X$ y completud de ${\mathbb{R}}^n$, tenemos que la sucesión converge a un punto $x_0$. Por continuidad, este punto satisface:

$$x_0=\underset{m\to \mathrm{\infty }}{lim}{x}_{m+1}=\underset{m\to \mathrm{\infty }}{lim}\phi (x_m)=\phi \left(\underset{m\to \mathrm{\infty }}{lim}{x}_m\right)=\phi (x_0).$$

La unicidad no necesita la compacidad de $X$, sino únicamente que $\phi$ sea contracción. En efecto, si hay otro punto fijo $x$ entonces

$$\Vert x-x_0\Vert =\Vert \phi (x)-\phi (x_0)\Vert \le \lambda \Vert x-x_0\Vert ,$$

de donde $\Vert x-x_0\Vert =0$, pues si no se tendría una contradicción. Así, $x=x_0$.

Desigualdades para la norma de Frobenius. Para $x\in {\mathbb{R}}^n$ y $A,B$ matrices reales de $n\times n$ tenemos que
a) $\Vert Ax\Vert \le \Vert A\Vert \Vert x\Vert$ y
b) $\Vert AB\Vert \le \Vert A\Vert \Vert B\Vert$.

La desigualdad (a) se prueba usando la desigualdad de Cauchy-Schwarz. En efecto, si $A_1,\dots ,A_n$ son los renglones de la matriz $A$, tenemos que $$Ax=(A_1\cdot x,A_2\cdot x,\dots ,A_n\cdot x),$$

entrada a entrada tenemos por Cauchy-Schwarz que

$$(A_i\cdot x{)}^2\le {\Vert A_i\Vert }^2{\Vert x\Vert }^2,$$

de modo que sumando para $i=1,\dots ,n$ tenemos que

$${\Vert Ax\Vert }^2\le \left(\sum _{i=1}^n{\Vert A_i\Vert }^2\right){\Vert x\Vert }^2={\Vert A\Vert }^2{\Vert x\Vert }^2,$$

lo cual prueba la desigualdad (a). La desigualdad (b) se prueba de manera similar, tomando fila por fila a la matriz $A$ y columna por columna a la matriz $B$.

Desigualdad del valor medio. Sea $U\subset {\mathbb{R}}^n$ un abierto convexo y $F:U\to {\mathbb{R}}^n$ una función de clase ${\mathcal{C}}^1$. Sean $x,y$ puntos en $U$ para los cuales la cual la norma de Frobenius del Jacobiano $\Vert DF\Vert$ está acotada sobre el segmento $xy$ por una constante $C$. Entonces:

$$\Vert F(x)-F(y)\Vert \le C\Vert x-y\Vert .$$

La desigualdad del valor medio requiere de algunos pasos intermedios. Definamos $h=y-x$. La clave es probar las siguientes tres afirmaciones:

$$\begin{array}{rl}F(x)-F(y)& ={\int }_0^{1}DF(x+th)hdt\\ \Vert {\int }_0^{1}DF(x+th)hdt\Vert & \le {\int }_0^1\Vert DF(x+th)\Vert \Vert h\Vert dt\\ {\int }_0^1\Vert DF(x+th)\Vert \Vert h\Vert dt& \le C\Vert h\Vert .\end{array}$$

La primera es una «generalización» del teorema del valor medio de una variable. Se prueba coordenada a coordenada usando el Teorema Fundamental del Cálculo, la regla de la cadena y un intercambio de integral con suma (usando la continuidad de las derivadas parciales).

La segunda se prueba usando desigualdad del triángulo para integrales y la desigualdad (a) que probamos arriba para la norma de Frobenius.

La tercera se sigue de manera inmediata de la cota hipótesis para la matriz Jacobiana, pues $x+th=x+t(y-x)$ recorre el segmento $xy$ conforme $t$ recorre el intervalo $[0,1]$.

Combinando las tres afirmaciones concluimos

$$\Vert F(x)-F(y)\Vert \le C\Vert h\Vert =C\Vert y-x\Vert ,$$

que es justo lo que queríamos probar.

Con esto terminamos los pre-requisitos para probar el TFI. Aquí ya se ve algo interesante sucediendo. En el TFI queremos mostrar que cierta restricción es biyectiva, osea que cierto sistema de ecuaciones tiene una y sólo una solución. Esto se asemeja al teorema del punto fijo de Banach, donde, bajo ciertas condiciones de contracción, hay uno y sólo un punto fijo. El teorema de la desigualdad media puede ayudar a mostrar que una función contrae. Todo esto no es casualidad. A continuación veremos cómo combinar estos ingredientes.

Demostración del TFI

Estamos listos para dar la demostración del teorema de la función inversa. Por comodidad, aquí lo enunciamos de nuevo:

Teorema de la función inversa. Sea $F:{\mathbb{R}}^n\to {\mathbb{R}}^n$ una función de clase ${\mathcal{C}}^1$ con matriz Jacobiana $DF$. Supongamos que $F(a)=b$ y que $DF(a)$ es invertible. Entonces existen vecindades abiertas $U$ y $V$ de $a$ y $b$ respectivamente para las cuales:

a) $F:U\to V$ es una biyección,
b) su inversa $F^{-1}:V\to U$ es de clase ${\mathcal{C}}^1$ y
c) $D{F}^{-1}(b)=DF(a{)}^{-1}$.

Para el teorema necesitamos definir quién es el abierto $U$. Lo tomaremos como $U:=B(a,ϵ)$, una bola abierta y centrada en $a$ de radio $ϵ$. La idea es tomar $ϵ$ tan pequeño como para que para $x\in U$ tengamos que $DF(x)$ sea invertible y

$$\Vert DF(a)-DF(x)\Vert \le \frac{1}{2\Vert DF(a{)}^{-1}\Vert }.$$

Ambas cosas las podemos hacer pues la asignación $x\mapsto DF(x)$ es continua ya que $F$ es de clase ${\mathcal{C}}^1$. En el transcurso de la prueba discutiremos la motivación de esta elección. A $V$ lo tomaremos como $F(U)$.

Lo primero que haremos es reformular parte (a) en términos de puntos fijos. Queremos que la restricción $F:U\to V$ que estamos buscando sea biyectiva. En otras palabras, para $y\in V$ queremos que la ecuación $y=F(x)$ tenga una y sólo una solución $x$ en $U$. Como por hipótesis la matriz $DF(a)$ es invertible, esto sucede si y sólo si

$$x+DF(a{)}^{-1}(y-F(x))=x,$$

es decir, si y sólo si $x$ es un punto fijo de la función ${\phi }_y(x)=x+DF(a{)}^{-1}(y-F(x))$. Parece un poco artificial haber introducido a $DF(a{)}^{-1}$, pero como veremos a continuación tiene sentido pues nos ayudará para que ${\phi }_y$ sea contracción.

Teniendo en mente que queremos usar la desigualdad del valor medio, calculamos y acotamos la norma de la derivada de ${\phi }_y$ como sigue

$$\begin{array}{rl}\Vert D{\phi }_y(x)\Vert & =\Vert I–DF(a{)}^{-1}DF(x)\Vert \\ & =\Vert DF(a{)}^{-1}(DF(a)–DF(x))\Vert \\ & \le \Vert DF(a{)}^{-1}\Vert \Vert DF(a)-DF(x)\Vert \end{array}$$

Aquí es donde usamos (y se motiva parte de) nuestra elección de $U$: nos permite acotar $\Vert DF(a)-DF(x)\Vert$ superiormente con $\frac{1}{2\Vert DF(a{)}^{-1}\Vert }$ y por lo tanto podemos concluir la desigualdad anterior como

$$\begin{array}{}\text{(1)}& \Vert D{\phi }_y(x)\Vert \le \frac{1}{2}.\end{array}$$

Por la desigualdad del valor medio, concluimos la siguiente observación clave.

Observacion. Para $y$ en $V$ tenemos que ${\phi }_y$ es contracción en $U$ con factor $\lambda =\frac{1}{2}$. En otras palabras, para $x,w$ en $U$, tenemos $$\Vert {\phi }_y(x)-{\phi }_y(w)\Vert \le \frac{\Vert x-x^{\prime }\Vert }{2}.$$

La prueba a partir de ahora se divide en los siguientes pasos:

1. Mostrar que $F:U\to V$ es biyectiva.
2. Mostrar que $V$ es abierto
3. Mostrar que $F^{-1}:V\to U$ es diferenciable y y $D{F}^{-1}(b)=DF(a{)}^{-1}$
4. Mostrar que las derivadas parciales son continuas

$F:U\to V$ es biyectiva.

La suprayectividad la tenemos gratis, pues por definición $V=F(U)$.

Para la inyectividad, tomamos $y\in V$ y supongamos que existen $x$ y $w$ en $U$ tales que $F(x)=y=F(w)$. Esto quiere decir que $x$ y $w$ son puntos fijos de la contracción ${\phi }_y$. Como vimos en la prueba del teorema del punto fijo de Banach, esto implica que $x=w$. Así, $x=w$, de modo que $F:U\to V$ es inyectiva y por lo tanto es biyectiva.

Nota: Aquí no estamos usamos el teorema del punto fijo de Banach pues $U$ no es compacto. Sólo estamos usando que las contracciones son inyectivas.

$V$ es abierto

Tomemos $y^{\prime }$ en $V$, es decir, para la cual existe $x^{\prime }$ en $U$ con $F(x^{\prime })=y^{\prime }$. Queremos ver que si «$y$ está muy cerquita de $y^{\prime }$» , entonces hay una solución para $F(x)=y$ con $x$ en $U$.

Como $U$ es abierto, existe $r$ tal que la bola $B(x^{\prime },2r)$ abierta de centro $x^{\prime }$ y radio $2r$ se queda contenida en $U$. Tomemos $y$ en la bola $B(y^{\prime },\frac{r}{2\Vert DF(a{)}^{-1}\Vert })$. Vamos a ver que $F(x)=y$ tiene solución en $U$. Consideremos la función ${\phi }_y$, pero restringida a la bola cerrada $X:=\bar{B}(x^{\prime },r)\subset U$. Mostraremos que la imagen de ${\phi }_y$ se queda contenida en $\bar{B}(x^{\prime },r)$. En efecto:

$$\begin{array}{rl}\Vert {\phi }_y(x)-x^{\prime }\Vert & =\Vert {\phi }_y(x)-{\phi }_y(x^{\prime })+DF(a{)}^{-1}(y-y^{\prime })\Vert \\ & \le \Vert {\phi }_y(x)-{\phi }_y(x^{\prime })\Vert +\Vert DF(a{)}^{-1}\Vert \Vert y-y^{\prime }\Vert \\ & \le \frac{\Vert x-x^{\prime }\Vert }{2}+\frac{r}{2}\le r.\end{array}$$

De este modo, ${\phi }_y$ es una contracción del compacto $X$ a sí mismo. Por lo tanto, tiene un punto fijo en $X$, de modo que $F(x)=y$ para $x\in X\subset U$. Esto muestra que $V=F(U)$ es abierto.

$F^{-1}:V\to U$ es diferenciable y $D{F}^{-1}(b)=DF(a{)}^{-1}$

Vamos a demostrar que $F^{-1}:V\to U$ es diferenciable a partir de la definición de diferenciabilidad. Más aún, veremos que si $y=F(x)$ para $x$ en $U$, entonces $D{F}^{-1}(y)=DF(x{)}^{-1}$. Aquí es donde se termina de motivar nuestra elección en $U$, pues nos garantiza que a la derecha en efecto tenemos una matriz invertible.

Tomemos entonces $y=F(x)$. Nos interesa el límite cuando $\Vert h\Vert \to 0$ de la siguiente expresión

$$\frac{\Vert F^{-1}(y+h)-F^{-1}(y)-DF(x{)}^{-1}h\Vert }{\Vert h\Vert },$$

Como $U$ es abierto, si $\Vert h\Vert$ es pequeña entonces $y+h$ está en $U$. De este modo, existe $k$ tal que $x+k\in U$ y $F(x+k)=y+h$. Así, la expresión anterior la podemos reescribir como

$$\begin{array}{}\text{(2)}& \frac{\Vert DF(x{)}^{-1}(F(x+k)-F(x)-DF(x)k)\Vert }{\Vert k\Vert }\frac{\Vert k\Vert }{\Vert h\Vert }\end{array}$$

Antes de continuar, probemos una desigualdad auxiliar. Notemos que

$$\begin{array}{rl}\Vert k\Vert -\Vert D{F}^{-1}(a)h\Vert & \le \Vert k-D{F}^{-1}(a)h\Vert \\ & =\Vert {\phi }_y(x+k)-{\phi }_y(x)\Vert \\ & \le \frac{\Vert k\Vert }{2},\end{array}$$

así,

$$\begin{array}{}\text{(3)}& \Vert k\Vert \le 2\Vert D{F}^{-1}(a)h\Vert \le 2\Vert D{F}^{-1}(a)\Vert \Vert h\Vert .\end{array}$$

Substituyendo el valor de $\Vert k\Vert$ en (2), concluimos que la expresión es menor o igual a

$$\begin{array}{}\text{(4)}& 2\Vert DF(x{)}^{-1}\Vert \frac{\Vert F(x+k)-F(x)-DF(x)k\Vert }{\Vert k\Vert }\Vert D{F}^{-1}(a)\Vert \end{array}$$

Estamos listos para terminar. La desigualdad (3) también garantiza que $\Vert k\Vert \to 0$ cuando $\Vert h\Vert \to 0$. Así, como $F$ es diferenciable, tenemos que la expresión (4) tiende a $0$. Esto muestra que $F^{-1}$ es diferenciable en $y$ con $D{F}^{-1}(y)=DF(x{)}^{-1}$, tal como queríamos.

Las derivadas parciales son continuas

Esta parte es sencilla a partir de la parte anterior. Tenemos que:

$$D{F}^{-1}(b)=DF(F^{-1}(b){)}^{-1}$$

Por la regla de Cramer la inversa de una matriz depende continuamente de las entradas de la matriz original. Además, la asignación $b\mapsto F^{-1}(b)$ es continua. Así, las entradas de $D{F}^{-1}(b)$ (las derivadas parciales de $F^{-1}$) dependen continuamente de las derivadas parciales de $F$, que dependen continuamente de $b$ por hipótesis.

Con esto termina la prueba.

¿Ahora qué?

Si te gustó esta entrada, puedes compartirla o revisar otras relacionadas con matemáticas a nivel universitario:

• Un ejemplo de aplicación del teorema de la función inversa
• Los teoremas fundamentales de los cuadraditos, o bien, una introducción amigable a los teoremas fundamentales del cálculo
• Un problema de probabilidad y escuchar música
• Mariposa de siete equivalencias de invertibilidad de matrices