Introducción
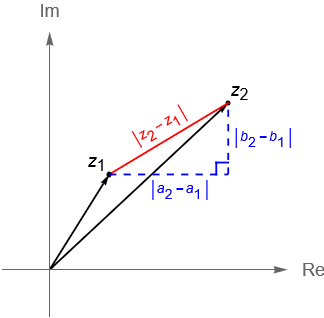
En la entrada anterior definimos el módulo de un número complejo en términos de su parte real e imaginaria. De manera geométrica observamos que el módulo nos determina la distancia que hay entre un número complejo y el origen. Por otra parte sabemos que el módulo en $\mathbb{C}$ cumple ciertas propiedades como el ser un número real no negativo y la desigualdad del triángulo. Por lo que razonando de manera análoga al caso en $\mathbb{R}^2$, mediante el módulo definiremos la distancia entre dos números complejos $z_1$ y $z_2$ como la longitud del segmento de recta que los une, figura 26.
El objetivo de esta entrada es describir algunos lugares geométricos en el plano complejo $\mathbb{C}$, haciendo uso de nuestros resultados de Geometría Analítica, para familiarizarnos con algunos conjuntos de puntos en el plano complejo con los cuales trabajaremos en la siguiente entrada y que en general nos serán de utilidad para describir de manera geométrica a los conjuntos de puntos de $\mathbb{C}$ que cumplan alguna propiedad en particular.
Métrica euclidiana en $\mathbb{C}$
Para comenzar esta entrada, primeramente consideremos la siguiente:
Definición 6.1. (Métrica euclidiana.)
Sean $z_1 = a_1 + ib_1$ y $z_2 = a_2 + ib_2$ números complejos. Definimos la distancia entre $z_2$ y $z_1$, denotada por $d(z_2, z_1)$, como:
\begin{equation*}
d(z_2, z_1) = |z_2 \, – \, z_1| = \sqrt{\left(a_2 \, – \, a_1\right)^2 + \left(b_2 \, – \, b_1\right)^2}.
\end{equation*}
A esta distancia se le conoce como la distancia o métrica euclidiana de $\mathbb{C}$, figura 26.
Por nuestros cursos de Geometría Analítica sabemos que al hablar de un lugar geométrico nos referimos a un conjunto de puntos que satisfacen una condición dada. Entonces podemos interpretar de manera geométrica a una ecuación como el lugar geométrico de los puntos en el plano cuyas coordenadas la satisfacen. En este sentido, consideraremos a los lugares geométricos del plano complejo como conjuntos de puntos en $\mathbb{R}^2$ que satisfacen una ecuación y viceversa, por lo que será necesario expresar en términos de números complejos las ecuaciones de los lugares geométricos de $\mathbb{R}^2$.
De acuerdo con las entradas anteriores sabemos que podemos ubicar a un número complejo en el plano, pensado como un par ordenado de números reales, en coordenadas cartesianas o coordenadas polares. Sin embargo, considerando la observación 2.3 sabemos que para $z\in\mathbb{C}$ se cumple:
\begin{equation*}
\text{Re}(z) = \frac{z+\overline{z}}{2}, \quad \text{Im}(z) = \frac{z-\overline{z}}{2i}. \end{equation*}
Lo anterior nos motiva a dar la siguiente:
Definición 6.2. (Coordenadas conjugadas complejas.)
Dado un número complejo $z = x+iy$, es posible representarlo en el plano complejo mediante las coordenadas $(z,\overline{z})$, a las cuales llamaremos coordenadas conjugadas complejas o simplemente coordenadas conjugadas considerando:
\begin{equation*}
x = \frac{z+\overline{z}}{2}, \quad y = \frac{z-\overline{z}}{2i}.
\end{equation*}
Observación 6.1.
Recordemos que para $A,C,D,E,F\in\mathbb{R}$ la ecuación general de segundo grado:
\begin{equation*}
Ax^2 + Cy^2 +Dx + Ey + F = 0, \tag{6.1}
\end{equation*}
nos determina algunos lugares geométricos en $\mathbb{R}^2$. Analicemos dos de ellos para identificarlos en el plano complejo.
- Dado $A=C=0$ en la ecuación (6.1), entonces se obtiene la ecuación general de la recta:
\begin{equation*}
Dx + Ey + F = 0.
\end{equation*}
De acuerdo con la definición 6.2, podemos expresar la ecuación de la recta utilizando coordenadas conjugadas como sigue:
\begin{align*}
D\left(\frac{z+\overline{z}}{2}\right) + E\left(\frac{z-\overline{z}}{2i}\right) + F = 0,\\
\\
\Longrightarrow \quad z\left(D-iE\right) + \overline{z}\left(D+iE\right) +2F = 0.
\end{align*}
Haciendo $a=D+iE$ y $b=2F$, tenemos:
\begin{equation*}
\mathcal{L}: \,\, z\overline{a}+\overline{z}a + b = 0, \tag{6.1.1}
\end{equation*}
la cual llamaremos ecuación general de la recta $\mathcal{L}$ en $\mathbb{C}$.
- Si tenemos $A=C\neq0$ en la ecuación (6.1), entonces se obtiene la ecuación general de la circunferencia:
\begin{equation*}
A(x^2+y^2) + Dx + Ey + F = 0.
\end{equation*}
De acuerdo con la definición 6.2, podemos expresar la ecuación general de la circunferencia utilizando coordenadas conjugadas como sigue:
\begin{align*}
A z\overline{z} + D\left(\frac{z+\overline{z}}{2}\right) + E\left(\frac{z-\overline{z}}{2i}\right) + F = 0,\\
\\
\Longrightarrow \quad z\overline{z} + z \left(\frac{D-iE}{2A}\right) + \overline{z}\left(\frac{D+iE}{2A}\right) + \frac{F}{A} = 0.
\end{align*}
Haciendo $a=\frac{D+iE}{2A}$ y $b=\frac{F}{A}$, tenemos:
\begin{equation*}
z\overline{z} + z\overline{a}+\overline{z}a + b = |\,z\,|^2 + z\overline{a}+\overline{z}a + b = 0, \tag{6.1.2}
\end{equation*}
la cual llamaremos ecuación general de la circunferencia en $\mathbb{C}$ cuyo centro es $-a$ y su radio es $\sqrt{|\,a\,|^2 – b}$.
Ejemplo 6.1.
Expresemos las siguientes ecuaciones en términos de las coordenadas conjugadas:
- a) Ecuación de una recta en el plano cartesiano $2x+3y=7$.
- b) Ecuación de una circunferencia en el plano cartesiano $x^2+(y-1)^2 = 25$.
Solución.
- a) De acuerdo con la observación 6.1 tenemos:
\begin{align*}
2\left(\frac{z+\overline{z}}{2}\right)+3\left(\frac{z-\overline{z}}{2i}\right)=7,\\
\\
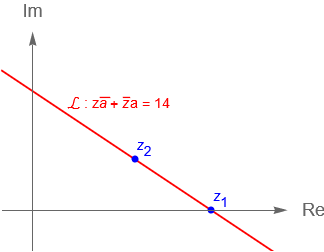
\Longrightarrow \quad \mathcal{L}: \,\, z\overline{a} + \overline{z}a = 14, \tag{6.1.3}
\end{align*}
con $a=2+3i$, la cual es la ecuación de una recta $\mathcal{L}$ en el plano complejo.
Considerando (6.1.3), notamos que los puntos $z_1 = 3{.}5$ y $z_2 = 2 + i$ pertenecen a la recta, figura 27.
- b) Notemos que:
\begin{equation*}
x^2 + (y-1)^2 = x^2 + y^2 -2y + 1 =25,
\end{equation*}
por lo que, considerando la observación 6.1, con $a = -i$ y $b = -24$ tenemos:
\begin{align*}
z\overline{z} – 2\left(\frac{z-\overline{z}}{2i}\right) -24 = 0,\\
\\
\Longrightarrow \quad z\overline{z} + z\overline{a} + \overline{z}a + b = 0, \tag{6.1.4} \end{align*}
la ecuación de una circunferencia en el plano complejo cuyo centro es $-a = i$ y su radio es $\sqrt{|i|^2 – (-24)} = \sqrt{25} = 5$, figura 32.
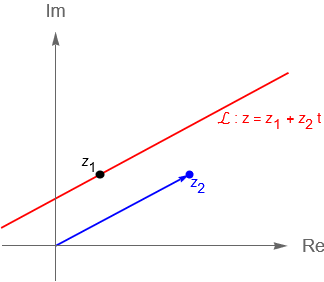
Al igual que en $\mathbb{R}^2$, es posible describir a la recta $\mathcal{L}$ en el plano complejo mediante su forma paramétrica considerando dos puntos $z_1,z_2\in\mathbb{C}$, $z_1\neq z_2$ y $z_2 \neq 0$, tales que $z_1$ está sobre la recta y el segmento de recta que va del origen a $z_2$ es paralelo a la recta, figura 28(a), entonces la recta $\mathcal{L}$ en $\mathbb{C}$, en su forma paramétrica, está dada como el conjunto de puntos $z\in\mathbb{C}$ tales que:
\begin{equation*}
z = z_1 + z_2t, \quad t\in\mathbb{R}. \tag{6.1.5}
\end{equation*}
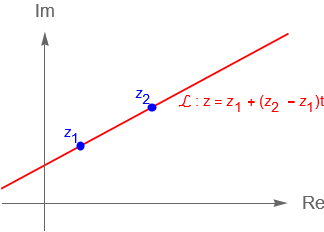
Si se tiene que $z_1$ y $z_2$, con $z_1\neq z_2$, son puntos de la recta, entonces la forma paramétrica de la ecuación de la recta $\mathcal{L}$, en $\mathbb{C}$, figura 28(b), se puede obtener como el conjunto de puntos $z\in\mathbb{C}$ tales que:
\begin{equation*}
z = z_1 + (z_2 \,-\, z_1)t, \quad t\in\mathbb{R}. \tag{6.1.6}
\end{equation*}
Figura 28: Gráficas de una recta en su forma paramétrica en $\mathbb{C}$.
Observación 6.2.
Dado que $z_2 \neq 0$ en (6.1.5), notemos que:
\begin{equation*}
t = \frac{z \,-\, z_1}{z_2} \in \mathbb{R} \quad \Longleftrightarrow \quad \operatorname{Im}\left(\frac{z \,-\, z_1}{z_2}\right) = 0,
\end{equation*}
por lo que una forma equivalente de expresar a una recta $\mathcal{L}$ dada por (6.1.5) es:
\begin{equation*}
\mathcal{L} = \left\{ z\in\mathbb{C} \,:\, \operatorname{Im}\left(\frac{z \,-\, z_1}{z_2}\right) = 0 \right\}.
\end{equation*}
Una pregunta interesante que podemos hacernos es ¿qué lugares geométricos describen las siguientes ecuaciones?
\begin{equation*}
\operatorname{Im}\left(\frac{z \,-\, z_1}{z_2}\right) > 0,
\end{equation*}
\begin{equation*}
\operatorname{Im}\left(\frac{z \,-\, z_1}{z_2}\right) < 0.
\end{equation*}
Analicemos la primera desigualdad. Sin pérdida de generalidad, desde que $z_2$ sólo nos determina la dirección de $\mathcal{L}$ entonces podemos suponer que $|\,z_2\,| = 1$. Sean $z_2 = \operatorname{cis}(\beta)$ y $z=r\,\operatorname{cis}(\theta)$.
Notemos que si $z_1=0$, tenemos por (6.1.5) una recta que pasa por el origen, además:
\begin{equation*}
\operatorname{Im}\left(\frac{z}{z_2}\right) = \operatorname{Im}\left(r\operatorname{cis}(\theta\,-\,\beta)\right) = r\operatorname{sen}(\theta-\beta) > 0,
\end{equation*}
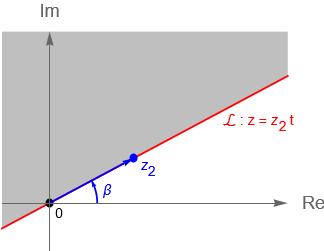
dado que $r=|\,z\,|\geq 0$, entonces $\operatorname{sen}(\theta-\beta) > 0$, lo cual se cumple si $\beta < \theta < \pi + \beta$. Por lo que la primera ecuación con $z_1 = 0$ nos describe un semiplano a la izquiera de la recta $\mathcal{L}$ que pasa por el origen, figura 29(a).
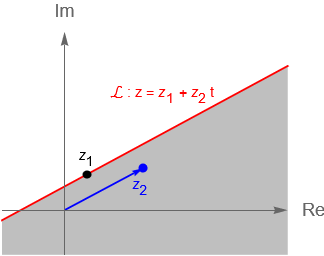
Si ahora consideramos el caso en que $z_1 \neq 0$, entonces por (6.1.5) tenemos una recta $\mathcal{L}$ que pasa por $z_1$ y es paralela a $z_2$, por lo que en dicho caso la ecuación $\operatorname{Im}\left(\dfrac{z \,-\, z_1}{z_2}\right) > 0$ nos describe al semiplano a la izquierda de la recta $\mathcal{L}$, figura 29(b).
Realizando un razonamiento análogo para la ecuación $\operatorname{Im}\left(\dfrac{z \,-\, z_1}{z_2}\right) < 0$, podemos concluir que dicha ecuación nos describe el semiplano a la derecha de una recta $\mathcal{L}$ que pasa por $z_1$ y es paralela a $z_2$, figura 30.
Figura 29: Gráficas de un semiplano izquierdo o superior en $\mathbb{C}$.

Observación 6.3.
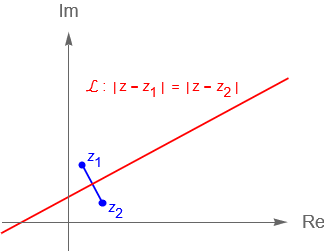
Otra forma de describir una recta $\mathcal{L}$ en el plano complejo $\mathbb{}$ es la siguiente. Sean $z_1, z_2 \in \mathbb{C}$, con $z_1 \neq z_2$. Notemos que la ecuación:
\begin{equation*}
|\,z \,-\, z_1\,| = |\,z \,-\, z_2\,|,
\end{equation*}
nos dice que la distancia de $z \in \mathbb{C}$ a los puntos $z_1$ y $z_2$ es la misma, es decir que $z$ está en la mediatriz del segmento que une a $z_1$ con $z_2$, figura 31.
Por otra parte, sabemos que la ecuación (6.1) determina otras cónicas además de la circunferencia, por lo que es posible proceder del mismo modo que en los dos casos de la observación 6.1 para obtener las ecuaciones correspondientes a dichos lugares geométricos. Sin embargo podemos hacer uso de la distancia euclidiana de $\mathbb{C}$ para describir dichos lugares geométricos mediante sus definiciones, es decir pensando a las cónicas como conjuntos de puntos que satisfacen ciertas condiciones relacionadas con la distancia entre puntos.
Consideremos el ejemplo 6.1, inciso b, sabemos que dicha circunferencia está centrada en $-a=i$ y tiene radio $\rho = 5$. De acuerdo con la definición de una circunferencia sabemos que los puntos cuya distancia al centro $i$ sea igual a 5 pertenecen a la circunferencia descrita por la ecuación (6.1.4), lo cual podemos expresarlo como el conjunto de números complejos $z$ tales que:
\begin{align*}
|\,z \,-\, i\,| = 5 \quad \Longleftrightarrow \quad |\,z \,-\, i\,|^2 = 25. \tag{6.1.7}
\end{align*}
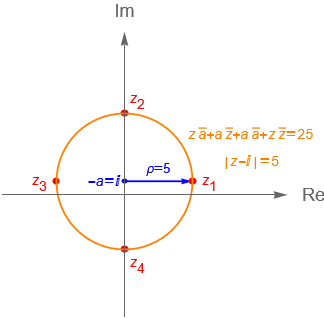
Notemos que podemos reescribir (6.1.7) como (6.1.4) utilizando las propiedades del módulo:
\begin{align*}
|\,z\,-\,i\,|^2 & = (z\,-\,i)\left(\overline{z}-\overline{i}\right)\\
& = |\,z\,|^2 – \, \overline{i}z -i\overline{z} + |\,i\,|^2\\
& = z\overline{z} + zi \, – \, \overline{z}i + 1\\
& = z\overline{z} + z\overline{a} + \overline{z}a + 1\\
& = 25.
\end{align*}
Considerando (6.1.7) es fácil ver que los puntos $z_1 = 5+i$, $z_2 = 6i$, $z_3 = -5 + i$ y $z_4 = -4i$ pertenecen a dicha circunferencia, figura 32.
Lo anterior nos deja ver que tanto (6.1.4) como (6.1.7) nos describen al mismo lugar geométrico en el plano complejo, es decir una circunferencia de radio $\rho=5$ centrada en $i$.
Podemos generalizar el resultado anterior para describir a una circunferencia en el plano complejo expresando a la ecuación (6.1.2) mediante la definición de dicho lugar geométrico, es decir, como el conjunto de números complejos $z$ que equidistan del punto $z_0=-a$, donde $a$ está dada como en (6.1.2), llamado centro, una distancia $\rho$, llamada radio:
\begin{equation*}
|\,z – z_0\,| = \rho \quad \Longleftrightarrow \quad |\,z – z_0\,|^2 = \rho^2. \tag{6.1.8}
\end{equation*}
Una pregunta que podemos plantearnos es ¿qué lugares geométricos nos describen las siguientes desigualdades?
\begin{align*}
|\,z – z_0\,| < \rho,\\
|\,z – z_0\,| > \rho.
\end{align*}
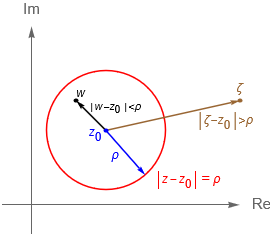
De manera geométrica es claro que la primera desigualdad nos describe a los puntos $z\in\mathbb{C}$ que se encuentran dentro de la circunferencia de radio $\rho$ y centro $z_0$, sin considerar propiamente a los que caen en dicha circunferencia. Mientras que la segunda desigualdad nos describe a los puntos en $z\in\mathbb{C}$ que caen fuera de la circunferencia centrada en $z_0$ y de radio $\rho$, sin considerar tampoco a los puntos de la circunferencia.
De acuerdo con la observación 3.3, tenemos que para un número complejo $z\neq0$:
\begin{equation*}
z^{-1} = \frac{1}{z} = \frac{\overline{z}}{| \, z \, |^2}.
\end{equation*}
Analicemos los siguientes casos:
- Si $|\,z\,|>1$, entonces $\dfrac{1}{|\,z\,|}<1$.
- Si $|\,z\,|<1$, entonces $\dfrac{1}{|\,z\,|}>1$.
- Si $|\,z\,|=1$, entonces $\dfrac{1}{|\,z\,|}=1$.
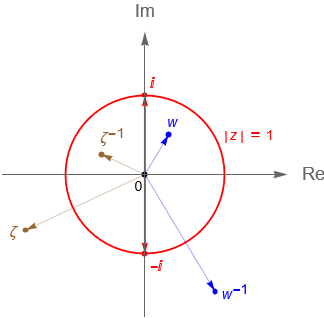
Geométricamente esto nos dice que para los números complejos $z$ que están fuera de la circunferencia unitaria su inverso multiplicativo está dentro de la circunferencia unitaria. Por otro parte, para los números complejos $z$ que están dentro de la circunferencia unitaria se tiene que su inverso multiplicativo está fuera de dicha circunferencia, mientras que para los números complejos $z$ que pertenecen a la circunferencia unitaria se tiene que su inverso multiplicativo también es un punto de dicha circunferencia.
Recordemos que en $\mathbb{R}^2$ la ecuación ordinaria de una circunferencia con centro en $(x_0, y_0)$ y radio $\rho$ es:
\begin{equation*}
(x-x_0)^2 + (y-y_0)^2 = \rho^2.
\end{equation*}
Haciendo $x(t) = \rho \operatorname{cos}(t) + x_0$ y $y(t) = \rho \operatorname{sen}(t) + y_0$, con $t\in[0,2\pi)$, obtenemos una ecuación paramétrica de dicha circunferencia.
Si consideramos a los números complejos $z$ en su forma polar, es decir $z=\rho \operatorname{cis}(\theta)$, tales que $\theta\in[0,2\pi)$, y a un punto fijo $z_0=x_0 + i y_0 \in\mathbb{C}$, entonces podemos describir a una cirunferencia en $\mathbb{C}$ de forma paramétrica como el conjunto de puntos:
\begin{equation*}
\{ w\in\mathbb{C} \, : \, w = z_0 + z \}.
\end{equation*}
Proposición 6.1. (Distancia de un punto a una recta en $\mathbb{C}$.)
Para un punto $z_0\in\mathbb{C}$, su distancia a una recta $\mathcal{L}$ dada por $z\overline{a} + \overline{z}a + b = 0$ está dada por:
\begin{equation*}
\frac{|\,z_0\overline{a} + \overline{z_0}a + b\,|}{2\,|\,a\,|}. \tag{6.1.9}
\end{equation*}
Demostración. Sea $z_0 = x_0 + iy_0\in\mathbb{C}$. Sabemos que en $\mathbb{R}^2$ la distancia de un punto $P(x_0,y_0)$ a una recta $Dx + Ey + F = 0$ está dada por:
\begin{equation*}
\frac{|\,Dx_0 + Ey_0 + F \,|}{\sqrt{D^2 + E^2}}. \tag{6.1.10}
\end{equation*}
De acuerdo con la observación 6.1 sabemos que podemos expresar una recta de la forma $Dx + Ey + F = 0$ como $z\overline{a} + \overline{z}a + b = 0$ donde $a = D + iE$ y $b=2F$. Por otra parte tenemos que:
\begin{equation*}
2D = a + \overline{a}, \quad i2E = a – \overline{a}.
\end{equation*}
Sea $z=x+iy$, entonces tenemos:
\begin{align*}
0 & = z\overline{a} + \overline{z}a + b\\
& = (x+iy)\overline{a} + (x-iy)a + b\\
& = x(a+\overline{a}) -iy (a-\overline{a}) + b\\
& = 2Dx +2Ey + 2F.
\end{align*}
Lo anterior nos deja ver que podemos utilizar (6.1.10) para obtener la distancia del punto $z_0 = x_0 + iy_0$ a la recta $z\overline{a}+\overline{z}a + b = 0$ como:
\begin{align*}
\frac{|\,Dx_0 + Ey_0 + F \,|}{\sqrt{D^2 + E^2}} &= \frac{|\,z_0\overline{a}+\overline{z_0}a + b \,|}{\sqrt{(a+\overline{a})^2 + \left(-i(a – \overline{a})\right)^2}}\\
& = \frac{|\,z_0\overline{a}+\overline{z_0}a + b \,|}{\sqrt{4\,|\,a\,|^2}}\\
& = \frac{|\,z_0\overline{a}+\overline{z_0}a + b \,|}{2\,|\,a\,|}.
\end{align*}
$\blacksquare$
Proposición 6.2. (Distancia de un punto a una recta en su forma paramétrica en $\mathbb{C}$.)
Sea $\mathcal{L}$ la recta en $\mathbb{C}$ dada por $z = z_1 + t z_2$, $z_2 \neq 0$. La distancia mínima $\delta$ de un punto $z_0 \in \mathbb{C}$ a la recta $\mathcal{L}$ es:
\begin{equation*}
\delta = \left|\, \frac{\operatorname{Im}\left((z-z_1)\overline{z_2}\right)}{\overline{z_2}} \,\right| = \left|\, \frac{(z – z_1)\overline{z_2} – \overline{(z-z_1)z_2}}{2\,\overline{z_2}} \,\right|.
\end{equation*}
Demostración. Sea $f(t) = |\,z \,-\, z_1 -tz_2\,|^2$. Es claro que $f:\mathbb{R} \longrightarrow [0,\infty)$ es una función bien definida.
De acuerdo con la proposición 3.1 tenemos que:
\begin{align*}
f(t) & = |\,z \,-\, z_1 -tz_2\,|^2\\
& = |\,z \,-\, z_1\,|^2 \,-\, 2t\,\operatorname{Re}\left((z-z_1)\overline{z_2}\right) + t^2 |\,z_2\,|^2.
\end{align*}
Derivando $f$ tenemos:
\begin{equation*}
f'(t) = -2\,\operatorname{Re}\left((z-z_1)\overline{z_2}\right) + 2t\, |\,z_2\,|^2.
\end{equation*}
Entonces el mínimo se alzanza en:
\begin{equation*}
t = \frac{\operatorname{Re}\left((z-z_1)\overline{z_2}\right)}{|\,z_2\,|^2}.
\end{equation*}
Dado que $z_2\neq0$, entonces $\dfrac{z_2}{|\,z_2\,|^2} = \dfrac{1}{\overline{z_2}}$.
Considerando la observación 2.3 y evaluando a $f$ en el mínimo obtenemos la distancia buscada al cuadrado, es decir:
\begin{align*}
\delta^2 &= \left|\,(z-z_1) \,-\, z_2\left[\frac{\operatorname{Re}\left((z-z_1)\overline{z_2}\right)}{|\,z_2\,|^2}\right] \,\right|^2\\
&= \left|\,\frac{2(z-z_1)\overline{z_2} \,-\, (z-z_1)\overline{z_2} \,-\, \overline{(z-z_1)}z_2}{2\, \overline{z_2}} \,\right|^2\\
&= \left|\,\frac{(z-z_1)\overline{z_2} \,-\, \overline{(z-z_1)}z_2}{2\, \overline{z_2}} \,\right|^2\\
&= \left|\,\frac{1}{\overline{z_2}}\frac{(z-z_1)\overline{z_2} \,-\, \overline{(z-z_1)}z_2}{2i} \,\right|^2\\
&=\left|\,\frac{\operatorname{Im}\left((z-z_1)\overline{z_2}\right)}{\overline{z_2}}\,\right|^2.
\end{align*}
Por lo que tomando raíz cuadrada se sigue el resultado.
$\blacksquare$
Es claro que al usar la definición de un lugar geométrico es posible asociarle una ecuación a dicho conjunto y representarlo en el plano complejo $\mathbb{C}$. Por ejemplo, recordemos las definiciones de los siguientes lugares geométricos:
- Parábola. Se define una parábola como el lugar geométrico de los puntos en $\mathbb{C}$ tales que la distancia entre estos y un punto fijo, llamado foco $f$, es igual a la distancia entre dichos puntos y una recta fija, llamada directriz $\mathcal{D}$.
Sin pérdida de generalidad, analicemos el caso de una parábola horizontal, es decir una parábola cuya directriz $\mathcal{D}$ es paralela al eje imaginario. En $\mathbb{R}^2$ sabemos que dichas rectas son de la forma $x = p$, con $p\in\mathbb{R}$ constante, por lo que para $z=x+iy\in\mathbb{C}$ tenemos que:
\begin{align*}
x \,-\, p = 0 \quad & \Longleftrightarrow \quad z+\overline{z} – 2p = 0\\
\\
& \Longleftrightarrow \quad \text{Re}(z) – p = 0. \tag{6.1.11}
\end{align*}
De acuerdo con (6.1.1), de la observación 6.1 tenemos que la ecuación de una directriz $\mathcal{D}$ paralela al eje imaginario cumple que $a=1$ y $b = -2p$, por lo que considerando la definición de la parábola y la proposición 6.1, tenemos que una parábola con foco $f\in\mathbb{C}$ y directriz $\mathcal{D}$ vertical dada por (6.1.11) es el lugar geométrico de los puntos $z\in\mathbb{C}$ tales que:
\begin{equation*}
\frac{|\,z + \overline{z}+ b\,|}{2\,} = |\,z-f\,|. \tag{6.1.12}
\end{equation*}
Observación 6.3.
Para el caso de una parábola vertical se procede de manera análoga utilizando el hecho de que para $z=x+iy\in\mathbb{C}$ se tiene que $y=\text{Im}(z)=\frac{z-\overline{z}}{2i}$ y que su directriz $\mathcal{D}$ es paralela al eje real.
Observación 6.4.
Considerando la definición de la párabola es posible obtener una ecuación más general que nos permita describir a dicho lugar geométrico. Suponiendo que la directriz $\mathcal{D}$ de una párabola está dada por la ecuación paramétrica $z_1 + tz_2$, con $t\in\mathbb{R}$, y que su foco es el punto $f\in\mathbb{C}$, entonces la ecuación de dicha párabola es:
\begin{equation*}
\left(\operatorname{Im}\left((z-z_1)\overline{z_2}\right)\right)^2 = |\,z_2\,|^2 \, |\,z-f\,|^2.
\end{equation*}
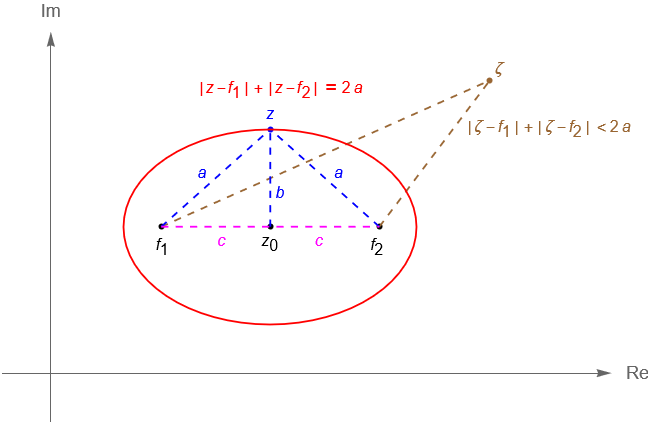
- Elipse. Se define a la elipse como el lugar geométrico de los puntos en $\mathbb{C}$ tales que la suma de sus distancias a dos puntos fijos $f_1,f_2\in\mathbb{C}$, llamados focos, es constante, es decir los $z\in\mathbb{C}$ tales que:
\begin{align*}
|\,z-f_1\,| + |\,z-f_2\,| = 2a,\\
\\
\text{con} \,\, 2a>|\,f_1 \,-\, f_2\,|.\tag{6.1.13}
\end{align*}
De acuerdo con nuestros cursos de Geometría sabemos que dados los focos de una elipse es posible identificar si se trata de una elipse vertical u horizontal, además al punto $z_0\in\mathbb{C}$ tal que $|\,z_0 \,-\, f_1\,| = |\,z_0 \,-\, f_2\,|=c$ se le conoce como el centro de la elipse y al valor $|\,f_1\,-\,f_2\,| =2c$ se le llama la distancia focal.
Por otra parte tenemos que la constante $2a$ determina al eje mayor, mientras que $\frac{|\,f_1\,-\,f_2\,|}{2a} = \frac{2c}{2a} = \frac{c}{a}$ nos da la excentricidad de la elipse.
¿Qué lugares geométricos nos describen las siguientes desigualdades?
\begin{align*}
|\,z-f_1\,| + |\,z-f_2\,| < 2a,\\
|\,z-f_1\,| + |\,z-f_2\,| > 2a.
\end{align*}
De manera geométrica es claro que la primera ecuación nos describe al conjunto de puntos $z\in\mathbb{C}$ que se encuentran dentro de la elipse con focos $f_1, f_2$ y con eje mayor $2a$. Por otra parte, la segunda ecuación nos describe a los $z\in\mathbb{C}$ que se encuentran fuera de dicha elipse, en ambos casos ninguna de las ecuaciones considera a los puntos $z\in\mathbb{C}$ que caen sobre la elipse, figura 36.
- Hipérbola. Se define a la hipérbola como el lugar geométrico de los puntos $z\in\mathbb{C}$ tales que el valor absoluto de las distancias a dos puntos fijos $f_1,f_2\in\mathbb{C}$, llamados focos, es igual a una cantidad constante, positiva y menor que la distancia entre los focos, es decir:
\begin{align*}
|\,|z-f_1|-|z-f_2|\,| = 2a,\\
\\
\text{con} \,\, 2a<|\,f_1 \,-\, f_2\,|.\tag{6.1.14}
\end{align*}
Donde $|\,f_1\,-\,f_2\,|=2c$ es la distancia focal y al punto $z_0\in\mathbb{C}$ tal que $|\,z_0\,-\,f_1\,|=|\,z_0\,-\,f_2\,|=c$ se le denomina el centro. La excentricidad de la hipérbola está dada por $\frac{|\,f_1\,-\,f_2\,|}{2a} = \frac{2c}{2a} = \frac{c}{a}$.
Observación 6.5.
Notemos que las ecuaciones (6.1.12), (6.1.13) y (6.1.14) obtenidas para estas tres cónicas corresponden a las ecuaciones ordinarias de las cónicas en $\mathbb{R}^2$, por lo que podemos preguntarnos sobre las ecuaciones generales para dichos lugares geométricos, solo recordemos que para hablar de estas expresiones debemos considerar los casos en que sea una cónica horizontal o vertical obtenidos de la ecuación (6.1). Recuerda que la ecuación (6.1) excluye a las cónicas que están rotadas en $\mathbb{R}^2$.
Observación 6.6.
Hasta ahora hemos utilizado las definiciones, como lugares geométricos, de estas tres cónicas para determinar sus ecuaciones. Sin embargo, de nuestros cursos de Geometría Analítica sabemos que es posible caracterizar a las cónicas mediante el concepto de excentricidad, es decir podemos determinar a las cónicas considerando a una recta fija $\mathcal{D}\in\mathbb{C}$, llamada directriz y a un punto fijo $f\in\mathbb{C}$, llamado foco. Si definimos a $e$ una cantidad positiva como la excentricidad, entonces el conjunto de puntos $z\in\mathbb{C}$ tales que la razón de su distancia a $f$ y a la recta $\mathcal{D}$ es siempre igual a $e$ es una sección cónica, la cual está dada por:
- a) Si $e < 1$, entonces es una elipse.
- b) Si $e = 1$, entonces es una párabola.
- c) Si $e > 1$, entonces es una hipérbola.
El caso en que $e=0$ nos determina una circunferencia.
Puedes consultar la sección 10.6 del libro Calculus: Early transcendentals de J. Stewart para revisar esta caracterización de las secciones cónicas en $\mathbb{R}^2$.
Considerando esta forma de determinar a las cónicas, es posible utilizar la ecuación de la párabola dada en la observación 6.5 para determinar a la elipse y la hipérbola.
Ejemplo 6.2.
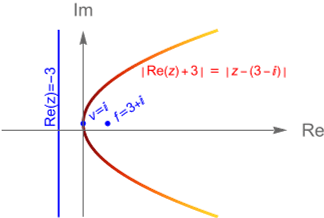
- a) Hallar la ecuación de la parábola cuyo foco está en $f=3+i$ y su directriz $\mathcal{D}$ está dada por $z+\overline{z}+6 = 0$.
Solución. De acuerdo con la definición de la parábola sabemos que se debe satisfacer (6.1.12), es decir:
\begin{align*}
\frac{|\,z + \overline{z}+ 6\,|}{2\,} = |\,z-(3+i)\,|\\
\\
\underset{(6{.}1{.}11)}{\Longleftrightarrow} \quad |\,\text{Re}(z) + 3\,|= |\,z-(3+i)\,|.
\end{align*}
Notemos que $\operatorname{Re}(z) + 3 \in \mathbb{R}$, por lo que, considerando la proposición 3.1:
\begin{align*}
|\,\text{Re}(z) + 3\,|^2= |\,z-(3+i)\,|^2\\
\\
\Longleftrightarrow \quad \left(\text{Re}(z) + 3\right)^2 = |\,z\,|^2 – 2\,\text{Re}(z(3-i)) + |\,3+i\,|^2.
\end{align*}
Desarrollando lo anterior y utilizando la proposición 3.1 tenemos:
\begin{equation*}
|\,z\,|^2 – \text{Re}^2(z) – 12\,\text{Re}(z) + 2\,\text{Re}(iz) + 1 = 0,
\end{equation*}
la cual es la ecuación de una parábola en $\mathbb{C}$ cuyo foco es $f=3+i$ y su directriz es $\text{Re}(z)=-3$, figura 37.
Si consideramos a $z=x+iy$, entonces la ecuación anterior corresponde a una parábola en $\mathbb{R}^2$ dada por:
\begin{equation*}
y^2-2y-12x+1=0.
\end{equation*}
- b) Hallar la ecuación de una elipse que tiene un foco $f_1 = -5+i$, su centro es $z_0 = x_0 +iy_0 = -1+i$ y que pasa por el punto $z_1=-1-2i$.
Solución. Considerando la definición de la elipse, el segundo foco $f_2$ debe satisfacer que $c=|z_0-f_2|=|z_0-f_1|=4$. De manera geométrica sabemos que $f_1, f_2$ y $z_0$ deben ser colineales, por lo que el segundo foco es $f_2 = (x_0+c)+i y_0 = (-1+4) + i = 3+i$. Considerando que $z_1=-1-2i$ pertenece a la elipse, entonces por (6.1.13) tenemos que:
\begin{align*}
|\,z_1-(-5+i)\,|+ |\,z_1-(3+i)\,| & = |\,4-3i\,| + |\,-4-3i\,|\\
& = 10\\
& = 2a.
\end{align*}
Entonces $a = 5$, por lo que la ecuación que describe a la elipse, figura 38, es:
\begin{equation*}
|\,z-f_1\,| + |\,z-f_2\,| = 10.
\end{equation*}
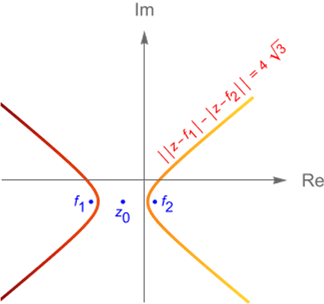
- c) Encontrar la ecuación de la hipérbola cuyos focos son $f_1=-(\sqrt{20}+3)-3i$, $f_2=(\sqrt{20}-3)-3i$ y que pasa por el punto $z_1=(\sqrt{12}-3)-3i$.
Solución. De acuerdo con la definición de la hipérbola, como el punto $z_1$ dado pertenece a dicho lugar geométrico entonces debe satisfacer (6.1.14), es decir:
\begin{align*}
|\,|\,z_1\,-\,f_1\,| – |\,z_1\,-\,f_2\,|\,| & = |\, |\,\sqrt{12}+\sqrt{20}\,| – |\,\sqrt{12}-\sqrt{20}\,|\,|\\
& = |\,4\sqrt{3}\,|\\
& = 4\sqrt{3}\\
& = 2a. \end{align*}
Entonces $a=2\sqrt{3}$, por lo que la ecuación de la hipérbola, figura 39, es:
\begin{equation*}
|\,|z+\sqrt{20}+3+3i|-|z-\sqrt{20}+3+3i|\,| = 4\sqrt{3}.
\end{equation*}
Tarea moral
- Considerando la definición de la parábola como lugar geométrico en $\mathbb{C}$, desarrolla la observación 6.3 y determina la ecuación de una parábola vertical. Argumenta tu resultado.
- La observación 6.4 nos proporciona una ecuación general de una párabola. Prueba dicha ecuación.
Hint: utiliza la proposición 6.3.
Comprueba con el ejemplo 6.2 inciso (a) que el resultado es correcto ¿Obtuviste la misma ecuación? - De acuerdo con la observación 6.5, desarrolla la ecuación (6.1) y trata de determinar las ecuaciones generales de las tres cónicas considerando coordenas conjugadas complejas.
- ¿Qué lugares geométricos representan las siguientes ecuaciones? Haz una representación de dichos conjuntos en el plano complejo $\mathbb{C}$.
- a) Los $z\in\mathbb{C}$ tales que $z = \overline{z}$.
- b) Los $z\in\mathbb{C}$ tales que $-\theta < \operatorname{Arg}\,z < \theta$.
- c) Los $z\in\mathbb{C}$ tales que $0 < \operatorname{Im}(z) < \pi$ y $-\pi < \operatorname{Re}(z) < \pi$.
- d) Los $z\in\mathbb{C}$ tales que $|\,z-1\,|^2+|\,z+1\,|^2<8$.
- e) Los $z\in\mathbb{C}$ tales que $|\,z-1-i\,|+|\,z+1+i\,|\leq 2$.
- Considera la definición de la hipérbola y la definición de la párabola ¿Es posible hablar de los puntos que se encuentran dentro y fuera de dichos lugares geométricos? Observa que en el caso de una circunferencia y una elipse dichos puntos se daban mediante las siguientes desigualdades respectivamente:
\begin{equation*}
|\,z-z_0\,| < \rho \quad \text{y} \quad |\,z-z_0\,| > \rho,
\end{equation*}
\begin{equation*}
|\,z-z_1\,| + |\,z-z_2\,| < 2a \quad \text{y} \quad |\,z-z_1\,| + |\,z-z_2\,| > 2a. \end{equation*}
- Sean $z_1, z_2, z_3\in\mathbb{C}$ tales que $|\,z_1\,| = |\,z_2\,| = |\,z_3\,|$ y $z_1 + z_2 + z_3 = 0$. Prueba que $z_1, z_2$ y $z_3$ son los vértices de un triángulo equilatero inscrito en la circunferencia unitaria.
- Muestra que el lugar geométrico de los puntos $z\in\mathbb{C}$ tales que $|\,z^2 – a^2\,| = a^2$, con $a\in\mathbb{R}$ una constante, es una lemniscata de Bernoulli.
- Sean $z_1, z_2, z_3\in\mathbb{C}$ los vértices de un triángulo en el plano complejo $\mathbb{C}$. Prueba que dicho triángulo es equilatero si y solo si:
\begin{equation*}
\frac{1}{z_1 – z_2} + \frac{1}{z_2 – z_3} + \frac{1}{z_3 – z_1} = 0,
\end{equation*}es decir si y solo si $z_1^2+z_2^2+z_3^2 = z_1 z_2 + z_2 z_3 + z_3 z_1$. - Sean $z_1,z_2,z_3\in\mathbb{C}$ tres puntos distintos. Prueba que dichos puntos caen en la misma recta si y solo si:
\begin{equation*}
\frac{z_1 – z_2}{z_1 – z_3} = t,
\end{equation*} donde $t$ es un número real.
Más adelante…
En esta entrada hemos definido la distancia entre dos puntos $z$ y $w$ en el plano complejo $\mathbb{C}$ siguiendo la idea de hablar de la distancia entre dichos puntos como la longitud del segmento de recta que los une, a la cual llamamos la distancia o métrica euclidiana. Dicha definición de distancia nos permitió describir algunos lugares geométricos en el plano complejo $\mathbb{C}$ haciendo uso de nuestros resultados de geometría y las propiedades del módulo en $\mathbb{C}$.
Es de nuestro interés describir estos lugares geométricos en el plano complejo $\mathbb{C}$ porque nos permite reconocer qué puntos pertenecen o no a un conjunto mediante una condición dada. Esto nos motivará a definir el concepto de disco o vecindad en la siguiente entrada, mediante el cual podremos caracterizar mejor a los conjuntos de $\mathbb{C}$ y con ello a los puntos que los conforman.
La siguiente entrada analizaremos a detalle la distancia recién definida y veremos que resulta ser una función definida en $\mathbb{C}\times\mathbb{C}$ y que toma valores en $[0, \infty)$, la cual recibe propiamente el nombre de métrica. Consideraremos al espacio métrico formado por $\mathbb{C}$ y la métrica euclidiana $d$ y describiremos la topología inducida en $\mathbb{C}$ por dicha métrica. Además probaremos algunos resultados de dicho espacio métrico.
Entradas relacionadas
- Ir a Variable Compleja I.
- Entrada anterior del curso: Potencias racionales y raíces en $\mathbb{C}$.
- Siguiente entrada del curso: Topología de $\mathbb{C}$.