Introducción
En la entrada anterior se dio el paso de generalizar la integral. Ya no solo considerarla como un valor, si no como una función.
Al momento de precisar esta generalización, pudimos encontrar el paralelismo que existe con la integral definida, lo podemos ver de la siguiente forma.
$$\text{Integral Definida} \Rightarrow \int \limits_a^b f(u) \ du.$$
$$\text{Integral Indefinida} \Rightarrow \int \limits_a^x f(u) \ du.$$
Como lo mencionamos anteriormente, la diferencia reside en el intervalo de integración, como se observa arriba sería el límite superior.
Pero, sin perdida de generalidad, se puede considerar el límite inferior o ambos, ya que el hecho de que sea indefinida es que no tiene un inicio o fin especifico, si no que estos dependen de una variable.
Entonces, el resultado de la integral no es un número real, ahora es una función que depende de la variable $x$, en este caso.
Y, dado que esta es nuestra única diferencia, se puede hacer analogía con las propiedades propuestas con la integral definida.
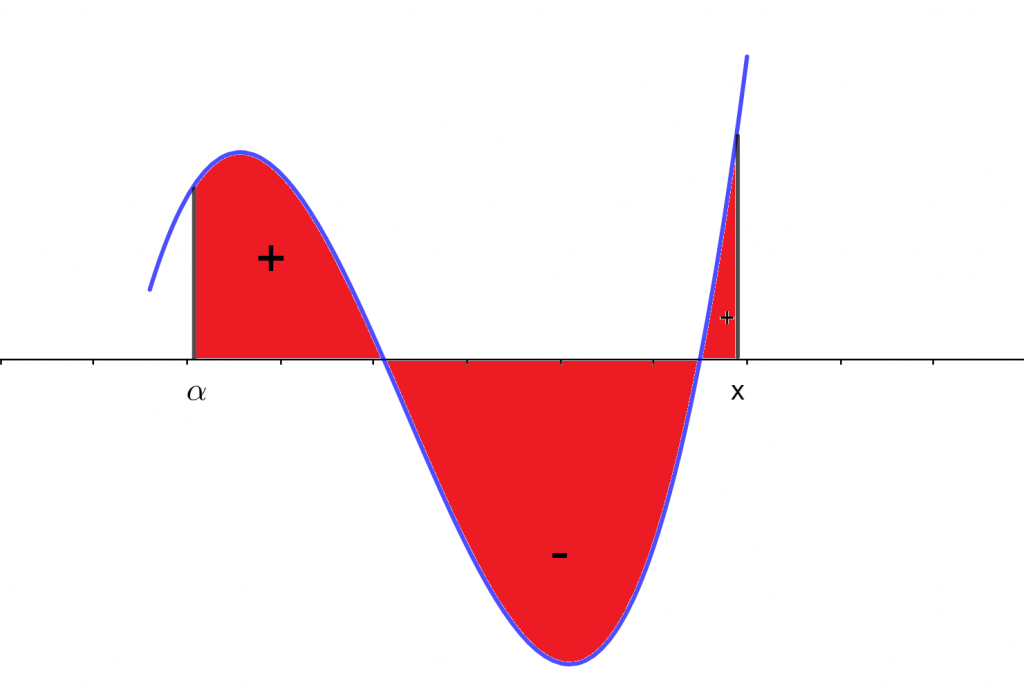
I. Aditividad
Considere un intervalo de integración $[a,x]$, y un punto $c$ dentro de este intervalo. $a<c<x.$
Entonces, la integral se puede separar de la siguiente forma.
$$ \int \limits_a^x f(u) \ du = \int \limits_a^c f(u) \ du + \int \limits_c^x f(u) \ du.$$
En este caso, se genera una integral definida y una integral indefinida.
Ejemplo:
Sea $f(u)$ la siguiente función.
$$f(u) =\left\lbrace\begin{array}{c} u^2 \ \ [0, 3] \\ sin(u) \ \ (3,10] \end{array}\right.$$
Se pueden tener diferentes casos al momento de pedir la integral de la función, ya que se puede partir el intervalo dependiendo del valor de $x$.
a) Si $ 0 \leq x \leq 3.$
Entonces, la integral de $f(u)$ se plantea como sigue.
$$\int \limits_0^x u^2 \ du.$$
Ya que es la parte donde la función tiene el dominio que se quiere integrar.
b) Si $ 3 < x \leq 10.$
Entonces la integral se ve de la siguiente manera.
$$\int \limits_3^x sin(u) \ du.$$
Y tenemos el mismo argumento que en el caso anterior.
c) Si $x \in [0,10] \ y \ x > 3.$
En este caso la $x$ corre en todo el intervalo y está condicionado que $x$ tiene que ser mayor que 3, entonces la integral se ve de la siguiente manera.
$$\int \limits_0^x f(u) \ du = \int \limits_0^3 u^2 \ du + \int \limits_3^x sin(u) \ du.$$
Y este caso, como se mencionó en la propiedad de la Aditividad, genera una integral definida y una integral indefinida.
d) Si $x \in [0,10] .$
Este caso solo condiciona a que el valor de $x$ tiene que estar dentro del dominio de la función, por lo que la integral queda de la siguiente manera.
$$ \int \limits_a^x f(u) \ du .$$
Y que se podrá dar solución en el momento en que se defina el valor de $x$.
II. Suma
Sea $h(u)$ una función tal que:
$$h(u) = f(u) + g(u).$$
Donde $f(u)$ y $g(u)$ también son funciones. Entonces, para calcular la integral de $h(x)$, tenemos la siguiente propiedad.
$$\int \limits_a^x h(u) \ du = \int \limits_a^x [f(u) \ + \ g(u)] \ du = \int \limits_a^x f(u) \ du + \int \limits_a^x g(u) \ du. $$
Entonces, la integral de una suma, es la suma de las integrales.
III. Producto por una constante
Sea $h(u)$ una función tal que $h(u)= c \cdot f(u)$, donde $c$ es cualquier real y $f(u)$ una función. Entonces,
$$\int \limits_a^x h(u) \ du = \int \limits_a^x c \cdot f(u) \ du = c \int \limits_a^x f(u) \ du.$$
Las constantes que se encuentran multiplicando a una función pueden entrar y salir de la integral.
IV. Linealidad
Sean $f(x)$ y $h(x)$ dos funciones y sean $\alpha$ y $\beta$ dos números reales. Entonces:
$$\int \limits_a^x [\alpha \ f(u) + \beta \ g(u)] \ du = \alpha \int \limits_a^x f(u) \ du + \beta \int \limits_a^x g(u) \ du.$$
Esta propiedad contiene a las dos anteriores (suma y producto), lo que la hace sumamente útil y provoca que se mencione en múltiples ocasiones.
Más adelante…
Ya que tenemos estás propiedades, podemos simplificar el proceso para desarrollar la integral y poder descomponerla en integrales más simples ó, en caso contrario, podemos aplicarlas para poder simplificarlas (reducirlas) o encontrar una sustitución adecuada para que se pueda integrar con mayor facilidad.
En la siguiente sección, tendremos un recordatorio de derivadas. Esto es necesario ya que existe una relación importante entre la derivada y la integral. Es posible que para este momento de tu formación, haz escuchado que la integral es el proceso contrario a o la inversa de la derivación.
Entonces, para poder explicar esta relación entre ambos procesos, es necesario recordar como funciona la derivada, que significa y como se calcula.
Tarea moral
- Utiliza la propiedad de linealidad.
$$\int \limits_a^x \alpha \ \left[ f(u) \ – \ g(u) + 1 \right] \cdot \beta \ h(u) \ du.$$ - Aplique las reglas correspondientes para expandir la forma de la integral, para los diferentes casos.
$$f(x) = \left\lbrace\begin{array}{c} 3x^2 \ – \ x + 13 \ \ [0, 5] \\ \frac{7}{x} \ \ (5,10] \end{array}\right.$$
i) Integral indefinida para cualquier $x$ entre 5 y 9.
ii) Integral indefinida para cualquier $x$ entre 0 y 5.
ii) Integral indefinida para cualquier $x$ entre 3 y 8, pasando por el 5. - Aplique las reglas correspondientes para dejar en una sola integral la siguiente integral.
$$1/7 \int \limits_a^x u^6 \ du \ – \ 7 \int \limits_a^x cos(u) \ du \ + \ 8 \int \limits_a^x \frac{1}{u+1} \ du.$$
Entradas relacionadas
- Página del curso: Cálculo Diferencial e Integral II
- Entrada anterior: La integral como función del límite superior – Integral Indefinida
- Entrada siguiente: Recordatorio de derivadas