Introducción
Esta es la segunda parte de la entrada anterior, donde presentamos el concepto de homotecia, en esta entrada nos enfocaremos en circunferencias homotéticas.
Homotecia de una circunferencia
Teorema 1. La homotecia de una circunferencia es una circunferencia.
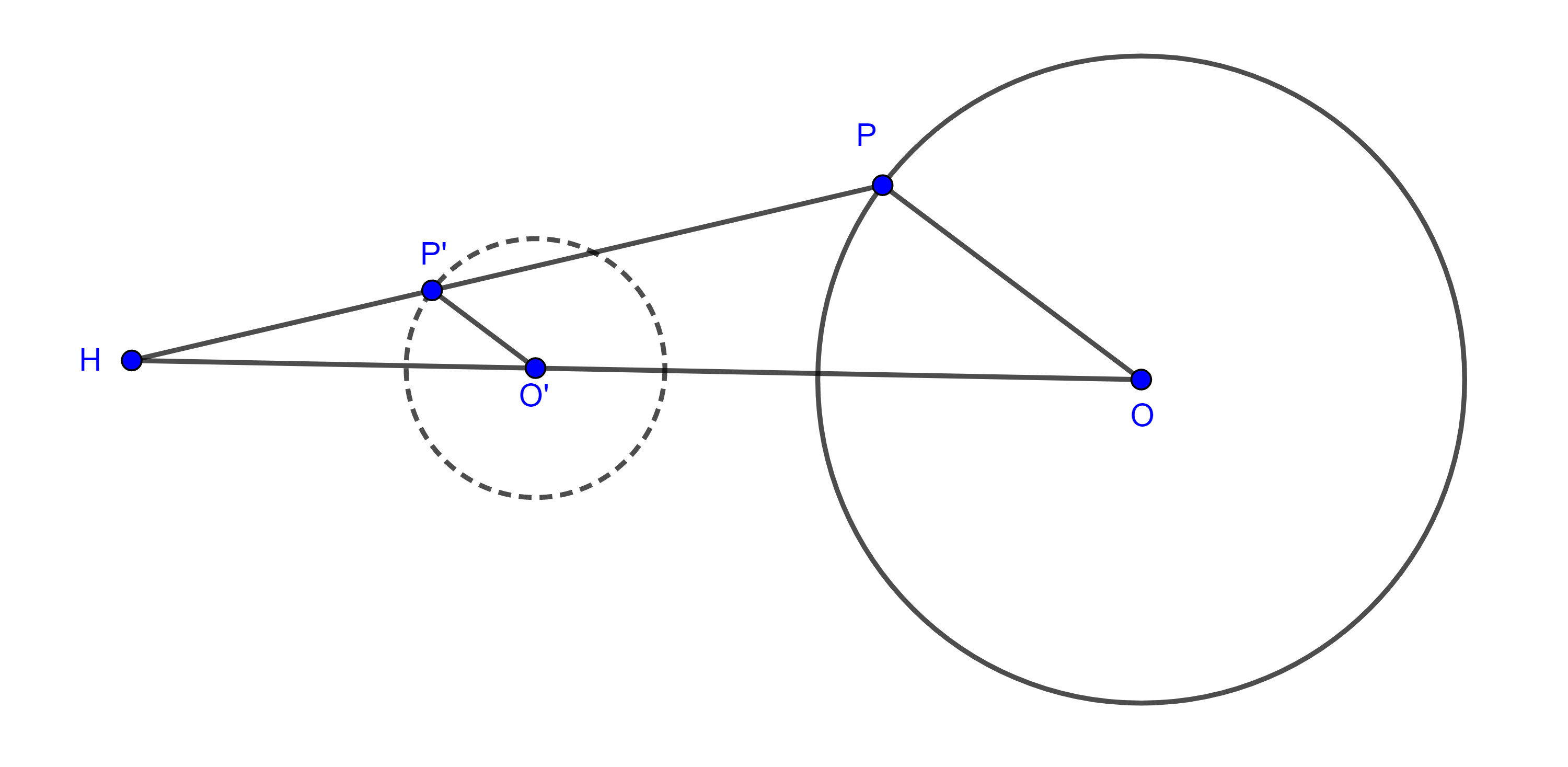
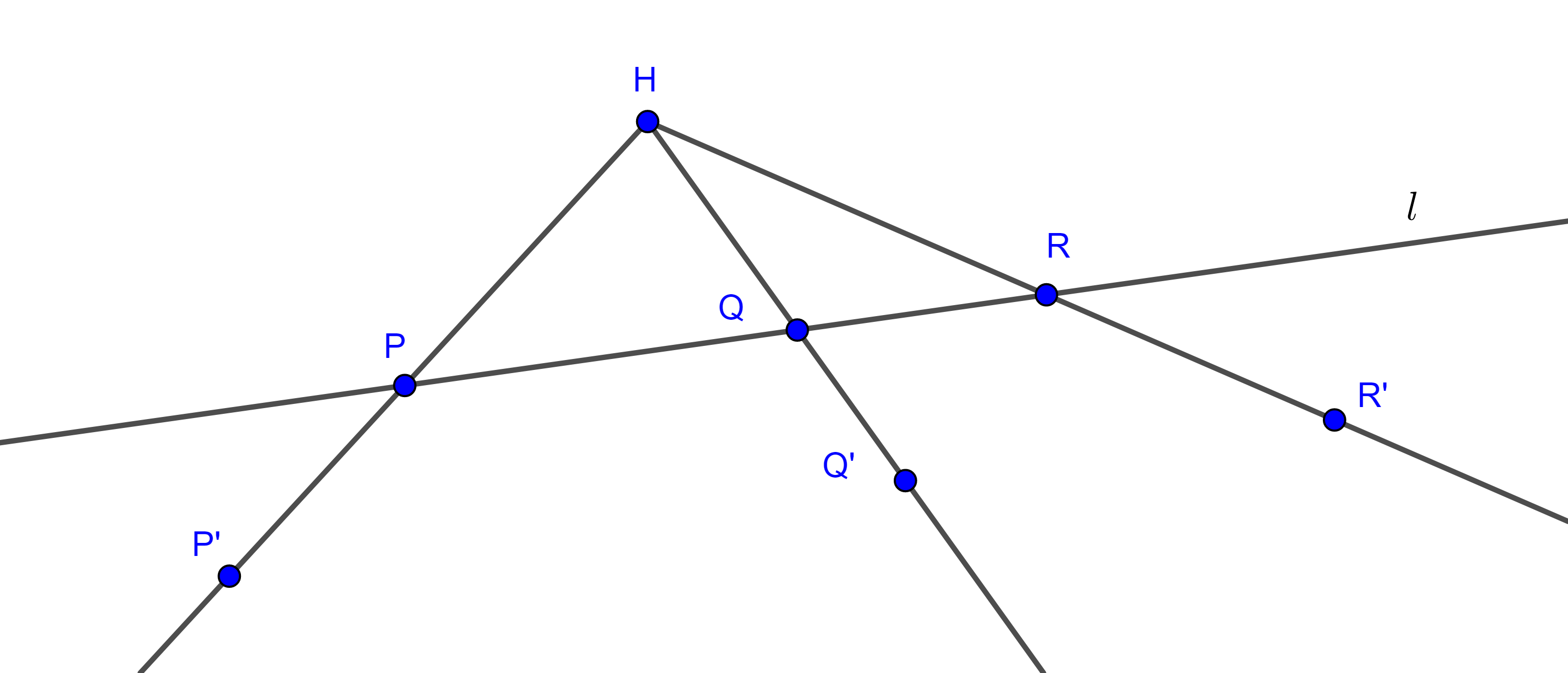
Demostración. Sea $(O, r)$ una circunferencia y consideremos una homotecia con centro en $H$ y razón $k$. Tomemos $P \in (O, r)$, y sean $P’$ y $O’$ los puntos homólogos de $P$ y $O$ respectivamente.
Como $P’O’ \parallel PO$ entonces $\triangle HO’P’ \sim \triangle HOP$
$\Rightarrow \dfrac{O’P’}{OP} = \dfrac{HP’}{HP} = k$
$\Rightarrow O’P’ = k \times OP = kr$
Por lo tanto, si $P$ describe una circunferencia, su punto homologo $P’$, se mueve a una distancia fija $kr$ de un punto fijo $O’$, esto es una circunferencia con centro en $O’$ y radio $r’ = kr$, $(O’, r’)$.
$\blacksquare$
Observaciones. Notemos que los respectivos centros $O$ y $O’$ son puntos homólogos y que la razón entre los radios de las circunferencias homotéticas es la razón de homotecia.
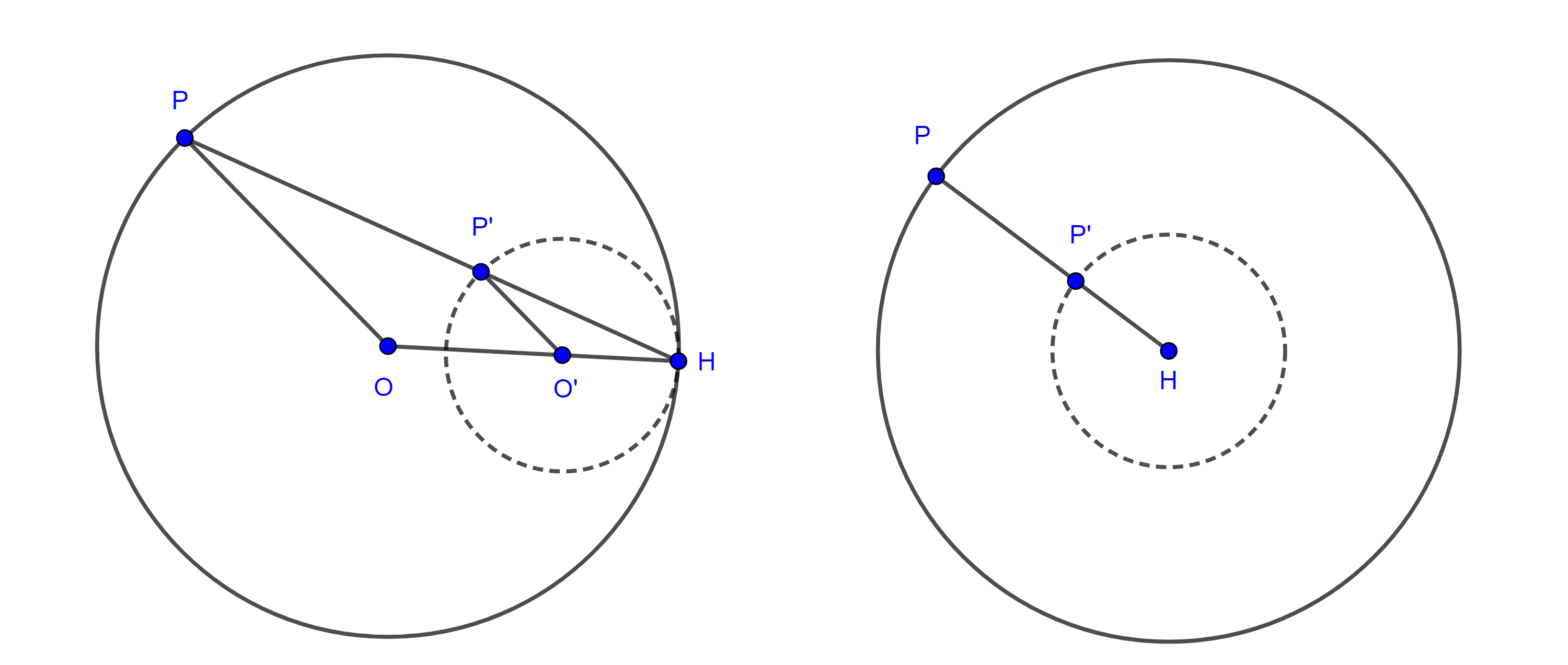
Recordemos que por convención, el punto homólogo del centro de homotecia es el mismo y como el centro de homotecia es colineal con los centros de las circunferencias homotéticas, si una de las circunferencias pasa por el centro de homotecia $H$, entonces la otra circunferencia también pasara por $H$ y ambas serán tangentes en $H$.
Si tomamos como centro de una circunferencia el centro de homotecia entonces las circunferencias homotéticas serán concéntricas.
Un triangulo variable
Teorema 2. Si un vértice de un triángulo variable esta sobre un punto fijo, un segundo vértice esta sobre una circunferencia dada y el triángulo variable siempre es semejante a un triángulo dado, entonces el tercer vértice del triángulo describe una circunferencia.
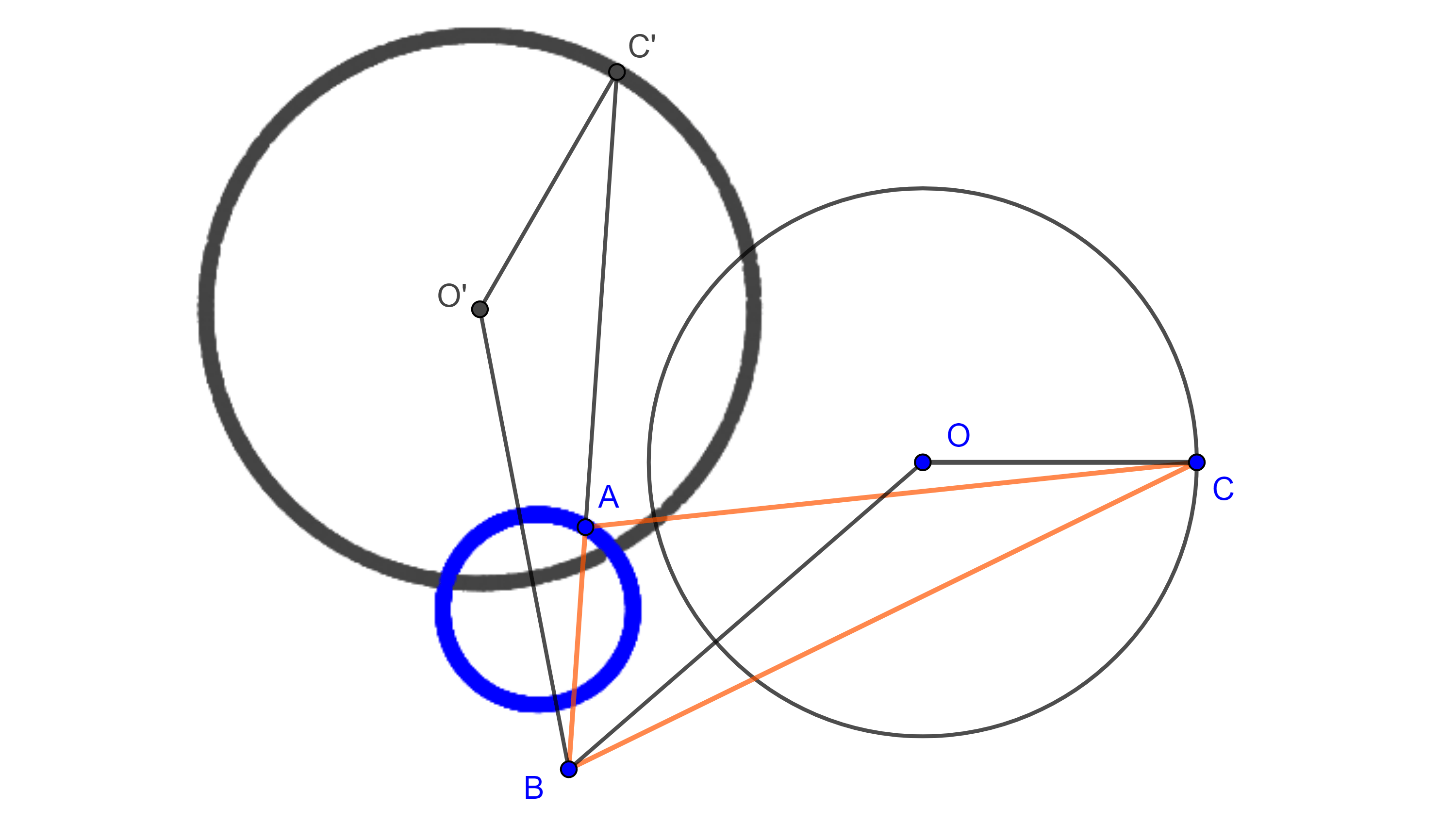
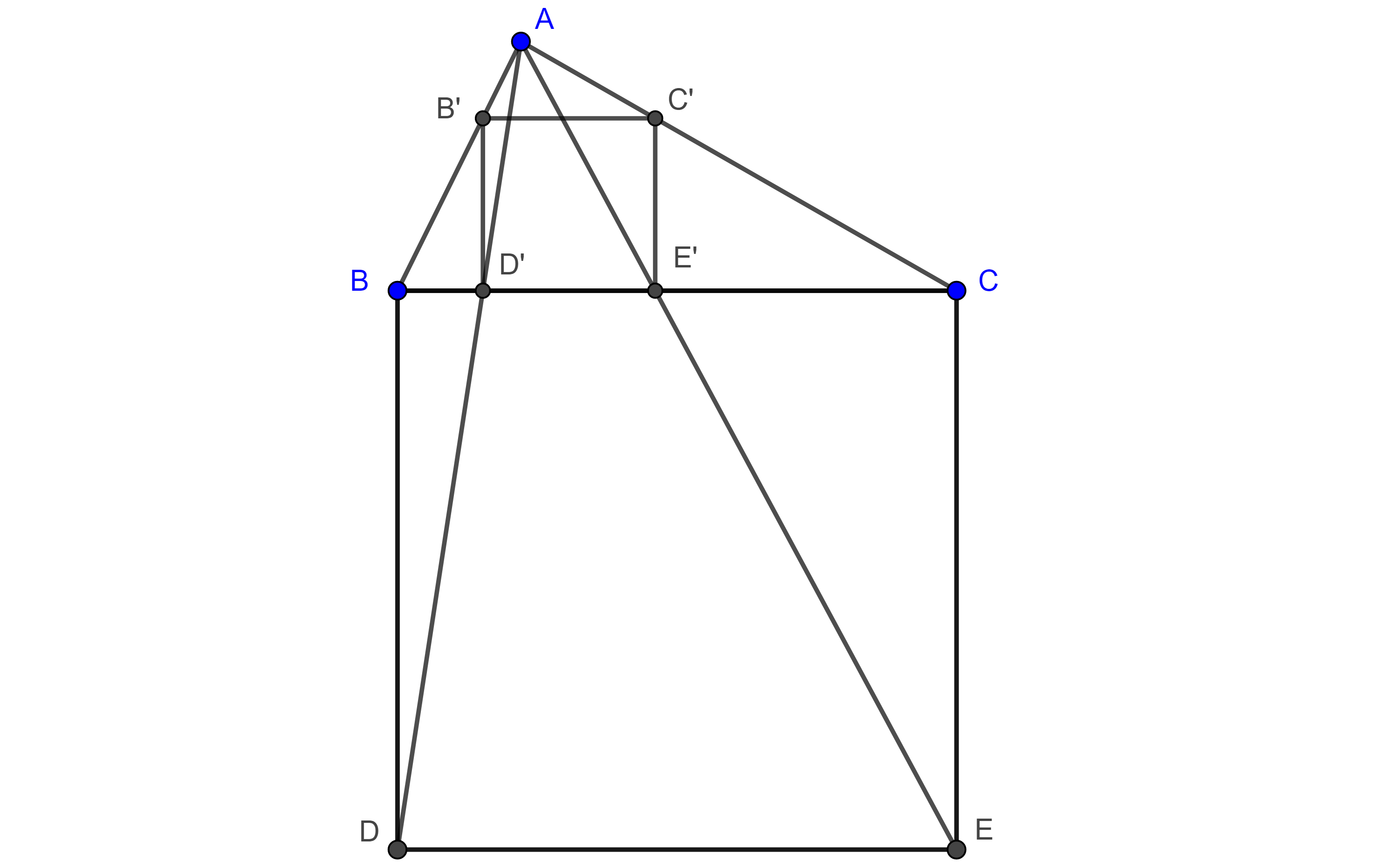
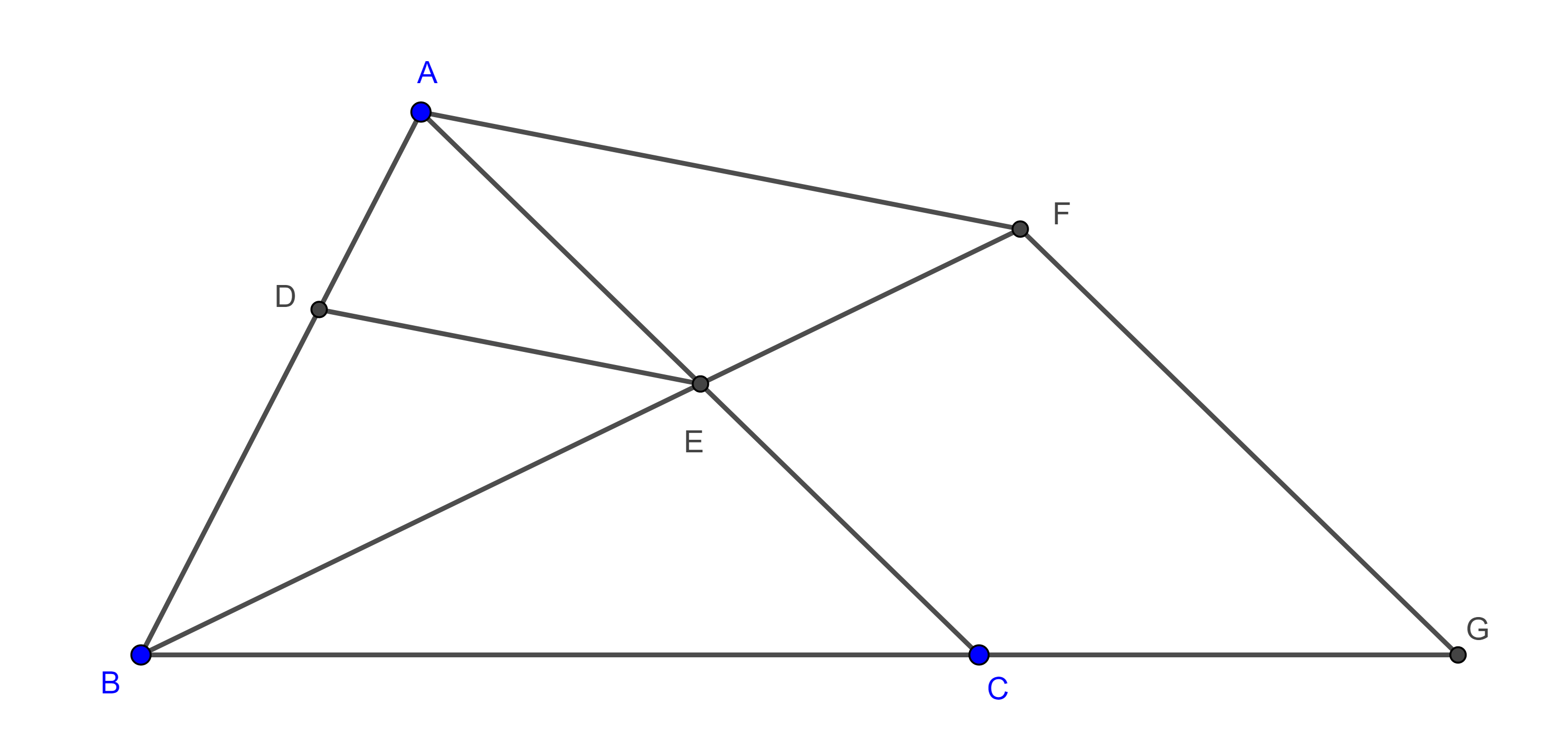
Demostración. Sea $\triangle ABC$ una de las posiciones del triángulo variable, donde $B$ es el punto fijo y $C$ está en $(O, r)$, la circunferencia dada.
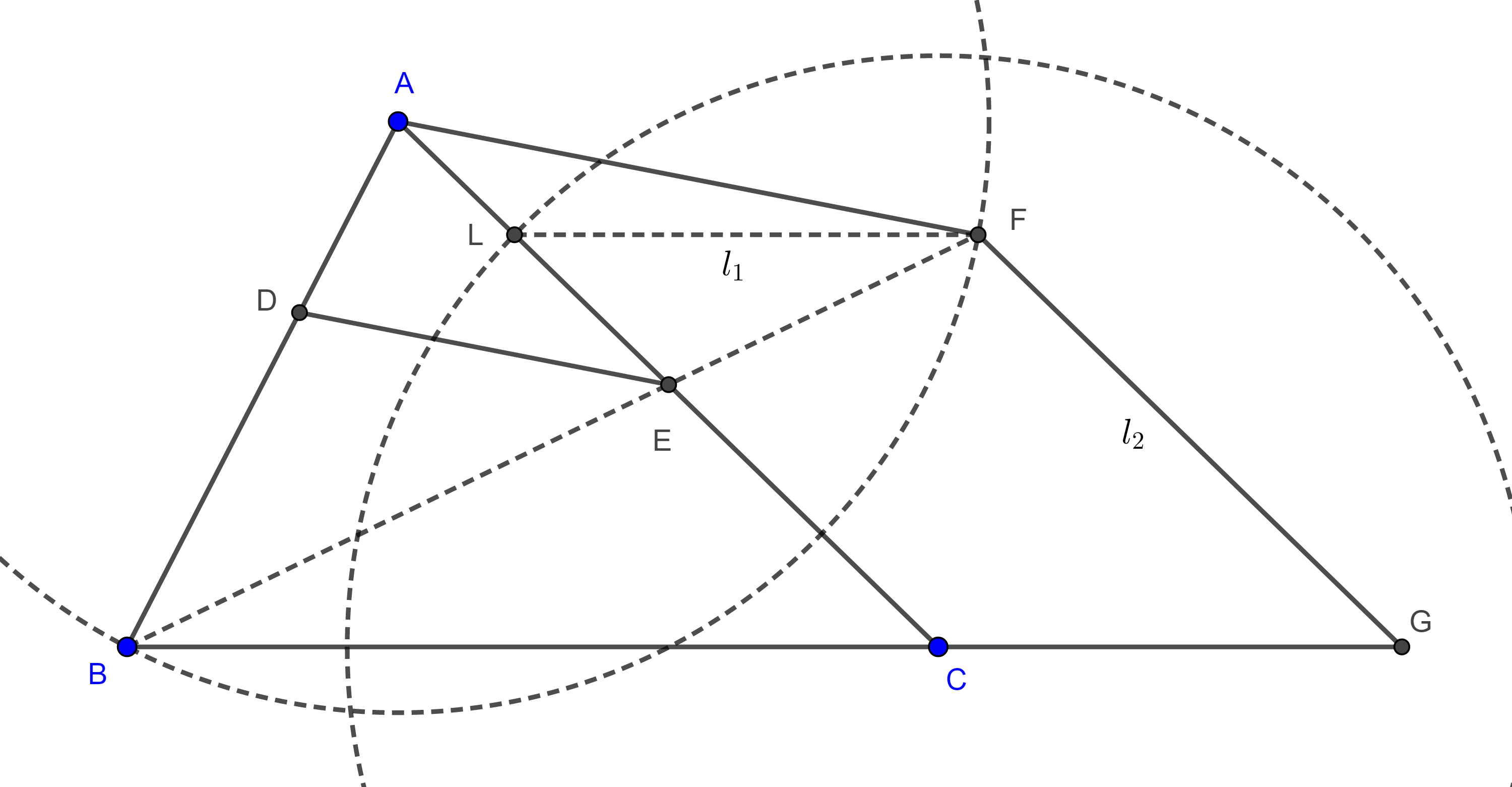
Sea $C’ \in AB$ tal que $BC’ = BC$, sobre $BC’$ construimos un triángulo $\triangle BO’C’$ congruente a $\triangle BOC$, de tal manera que sea posible a través de una rotación con centro en $B$ superponer $\triangle BOC$ con $\triangle BO’C’$.
Como $\angle OBC = \angle O’BC’$ entonces $\angle OBO’ = \angle CBC’ = \angle CBA$, este último ángulo es fijo por lo que la dirección de la recta $BO’$ es fija.
$BO’ = BO$ entonces $O’$ es un punto fijo para cualquier otra posición del triángulo variable $\triangle ABC$.
Como $CO’ = CO = r$, entonces todos los puntos $C’$ se mueven a una distancia fija $r$ de un punto fijo $O’$, por lo tanto, $C’$ describe una circunferencia.
Ya que $\dfrac{BA}{BC’} = \dfrac{BA}{BC}$ y esta última razón es fija, pues todos los triángulos $\triangle ABC$ son semejantes entre sí, $A$ y $C’$ son puntos homólogos de una homotecia con centro en $B$ y razón $\dfrac{BA}{BC}$, y como $C’$ describe una circunferencia, entonces por el teorema 1, $A$ también describe una circunferencia.
$\blacksquare$
Observación. Notemos que en el punto fijo se puede construir cualquiera de los tres ángulos dados, así, en el vértice que esta en el circulo dado tenemos otras dos elecciones, y el tercer vértice lo podemos construir a ambos lados del segmento $BC$, con lo que en total existen $12$ circunferencias diferentes que puede describir el tercer vértice.
Homotecia entre dos circunferencias dadas
Teorema 3. Dadas dos circunferencias de centros o radios distintos, siempre es posible encontrar una homotecia entre las dos.
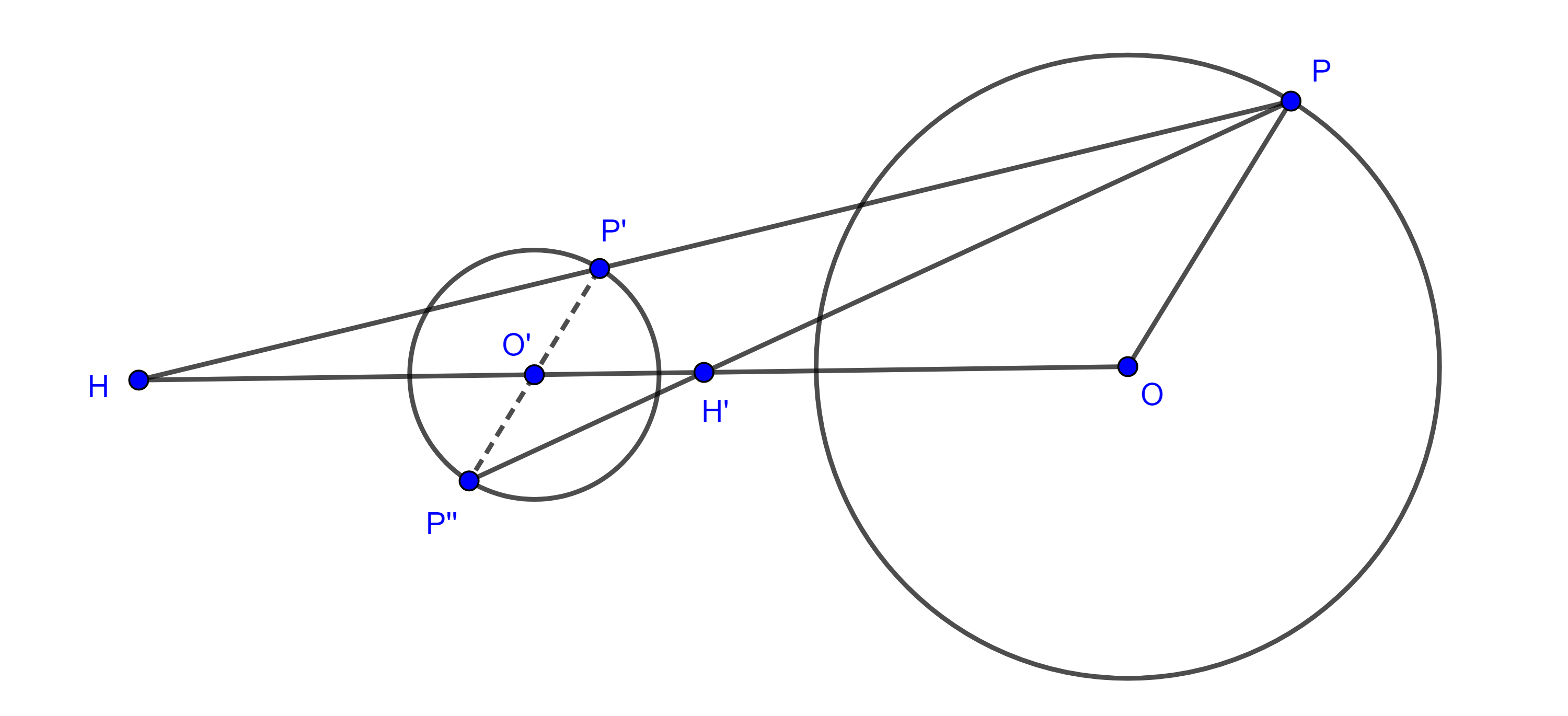
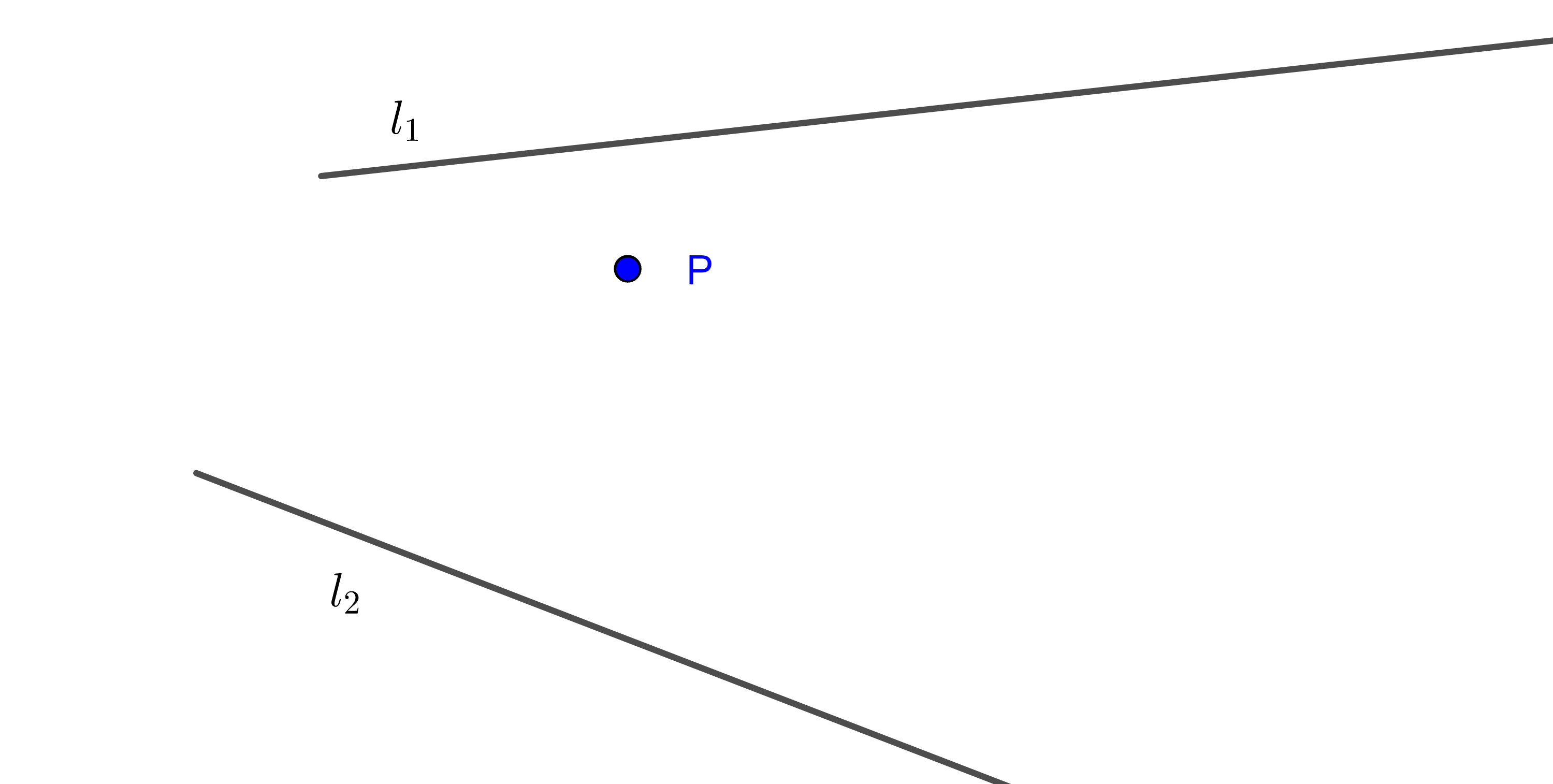
Demostración. Sean $(O, r)$ y $(O’, r’)$ tal que $O \neq O’$ y $r \neq r’$, tomemos $P \in (O, r)$ y tracemos por $O’$ un radio $O’P’$ paralelo a $OP$, sea $H = OO’ \cap PP’$.
Entonces $\triangle HO’P’ \sim \triangle HOP$
$\Rightarrow \dfrac{HP’}{HP} = \dfrac{HO’}{HO} = \dfrac{O’P’}{OP} = \dfrac{r’}{r}$.
En consecuencia, la homotecia con centro en $H$ y razón $k = \dfrac{r’}{r}$ lleva a $(O, r)$ en $(O’, r’)$.
Ahora consideremos $P’’$ el punto diametralmente opuesto a $P’$ en $(O’, r’)$, sea $H’ = OO’ \cap PP’’$, entonces $\triangle H’O’P’’ \sim \triangle H’OP$
$\Rightarrow \dfrac{H’P’’}{H’P} = \dfrac{H’O’}{H’O} = \dfrac{O’P’’}{OP} = \dfrac{r’}{r} = k$.
Así, hemos encontrado dos homotecias entre $(O, r)$ y $(O’, r’)$.
$\blacksquare$
Observación. Si las circunferencias son concéntricas entonces solo hay una homotecia entre ellas, la que tiene como centro el centro de las circunferencias.
Si las circunferencias tienen el mismo radio entonces la única homotecia entre ellas es la que tiene como centro el punto medio del segmento que une los radios.
Corolario 1. Rectas tangentes comunes a dos circunferencias pasan por un centro de homotecia.
Demostración. Supongamos que $TT’$ es una recta tangente exterior (es decir, la recta $TT’$ corta al segmento $OO’$ exteriormente) a dos circunferencias $(O, r)$ y $(O’, r’)$, donde $T \in (O, r)$ y $T’ \in (O’, r’)$.
Sea $H = OO’ \cap TT’$, como $O’T’ \parallel OT$ entonces $\triangle HO’T’ \sim \triangle HOT$
$\Rightarrow \dfrac{HT’}{HT} = \dfrac{HO’}{HO} = \dfrac{O’T’}{OT} = \dfrac{r’}{r}$.
Como el punto que divide externamente al segmento $OO’$ en la razón $\dfrac{r’}{r}$ es único, entonces $H$ es un centro de homotecia de $(O, r)$ y $(O’, r’)$.
Es análogo ver que las tangentes internas de dos circunferencias pasan por un centro de homotecia.
$\blacksquare$
Incírculo y exírculo en homotecia
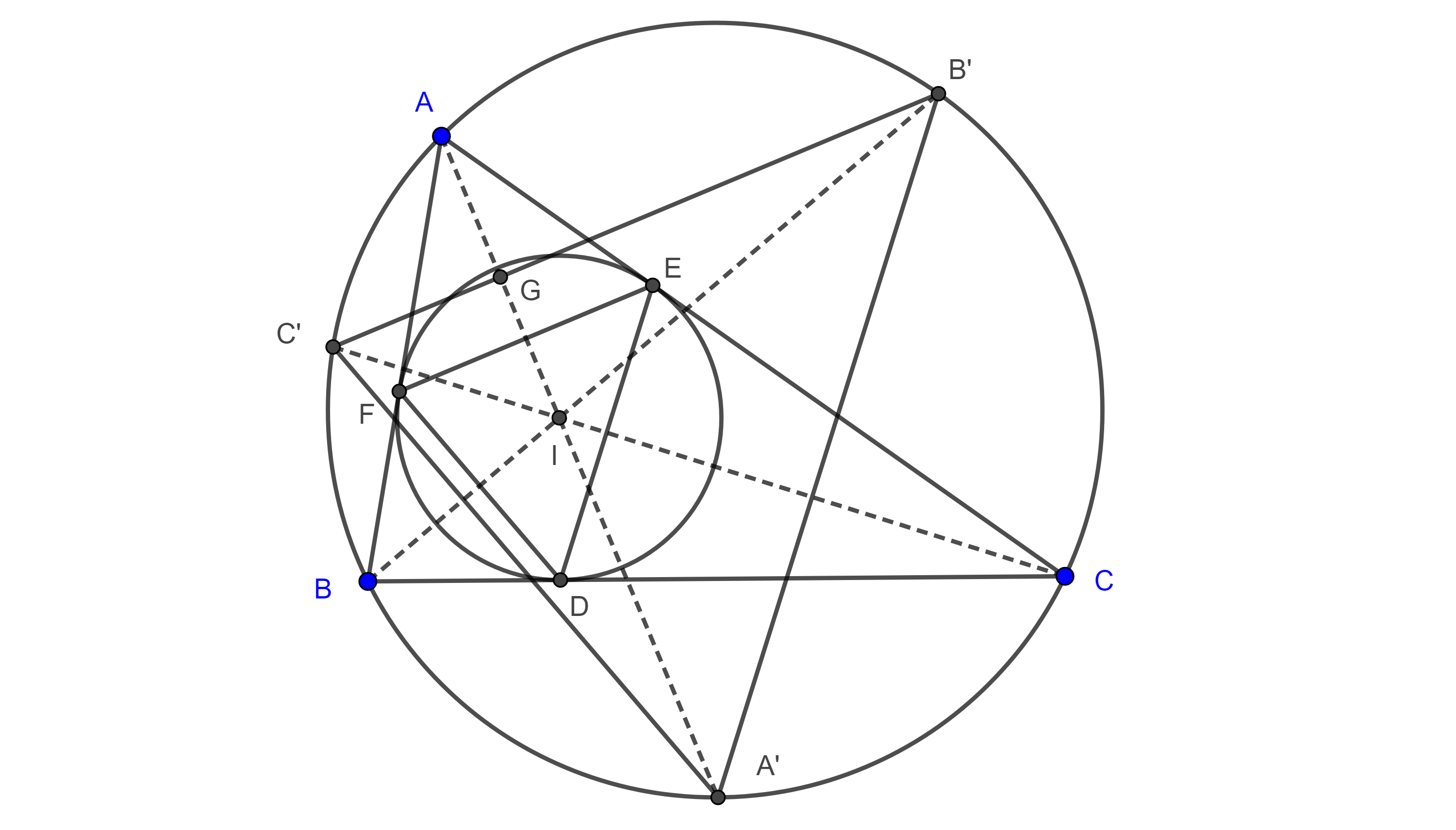
Teorema 3. Sea $\triangle ABC$, considera $(I, r)$ y $(I_b, r_b)$ su incírculo y $B$-excírculo respectivamente, sean $D$ el punto de tangencia de $AC$ con $(I, r)$ y $D’$ el punto diametralmente opuesto a $D$ en $(I, r)$, sea $E = BD’ \cap AC$, entonces $E$ es el punto de tangencia de $AC$ con $(I_b, r_b)$ y el punto medio de $AC$ es el punto medio de $DE$.
Demostración. Por el corolario 1, existe una homotecia con centro en $B$ y razón $\dfrac{r_b}{r}$ que lleva a $(I, r)$ en $(I_b, r_b)$, sea $X \in (I_b, r_b) $ el punto correspondiente a $D’ \in (I, r)$ bajo esta transformación.
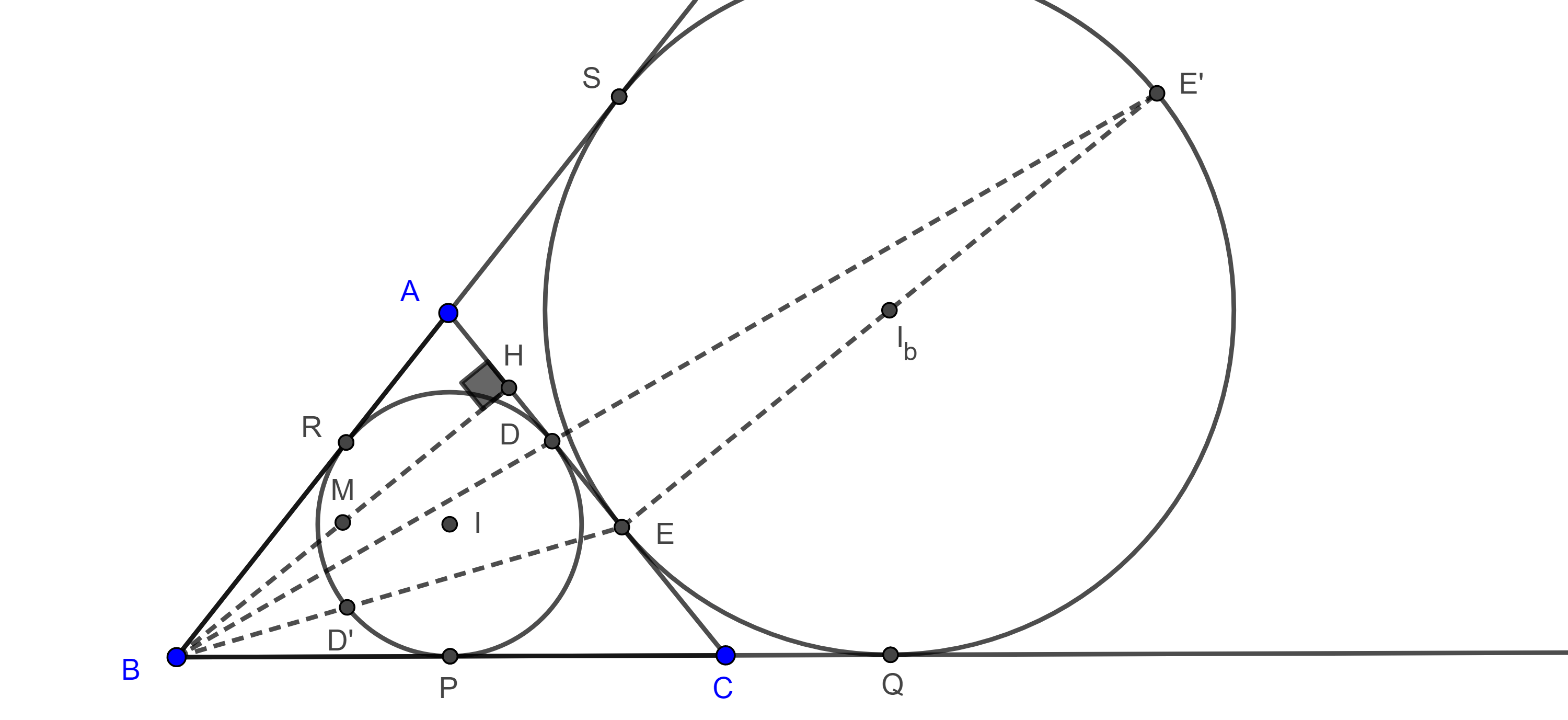
Entonces $ID’ \parallel I_bX$, pero $ID’ \perp AC$ $\Rightarrow I_bX \perp AC$ y como $AC$ es tangente a $(I_b, r_b)$ entonces $X \in AC$.
Como $X \in AC$ y $X$ es colineal con $B$ y $D’$ entonces $X = E$, así, $AC$ es tangente a $(I_b, r_b)$ en $E$.
Por otro, lado sean $P$, $Q$ los puntos de tangencia de $BC$ con $(I, r)$ y $(I_b, r_b)$ respectivamente y sean $R$, $S$ los puntos de tangencia de $AB$ con $(I, r)$ y $(I_b, r_b)$ respectivamente.
Recordemos que las tangentes desde un punto externo a una circunferencia son iguales.
$BP + PC + CQ = BQ = BS = BR + RA + AS \Rightarrow PC + CQ = RA + AS$
$\Rightarrow CD + CE = AD + AE \Rightarrow 2CE + DE = 2AD + DE$
$\Rightarrow CE = AD$
Por lo tanto, el punto medio de $AC$ es el punto medio de $DE$.
$\blacksquare$
Concurrencia de rectas
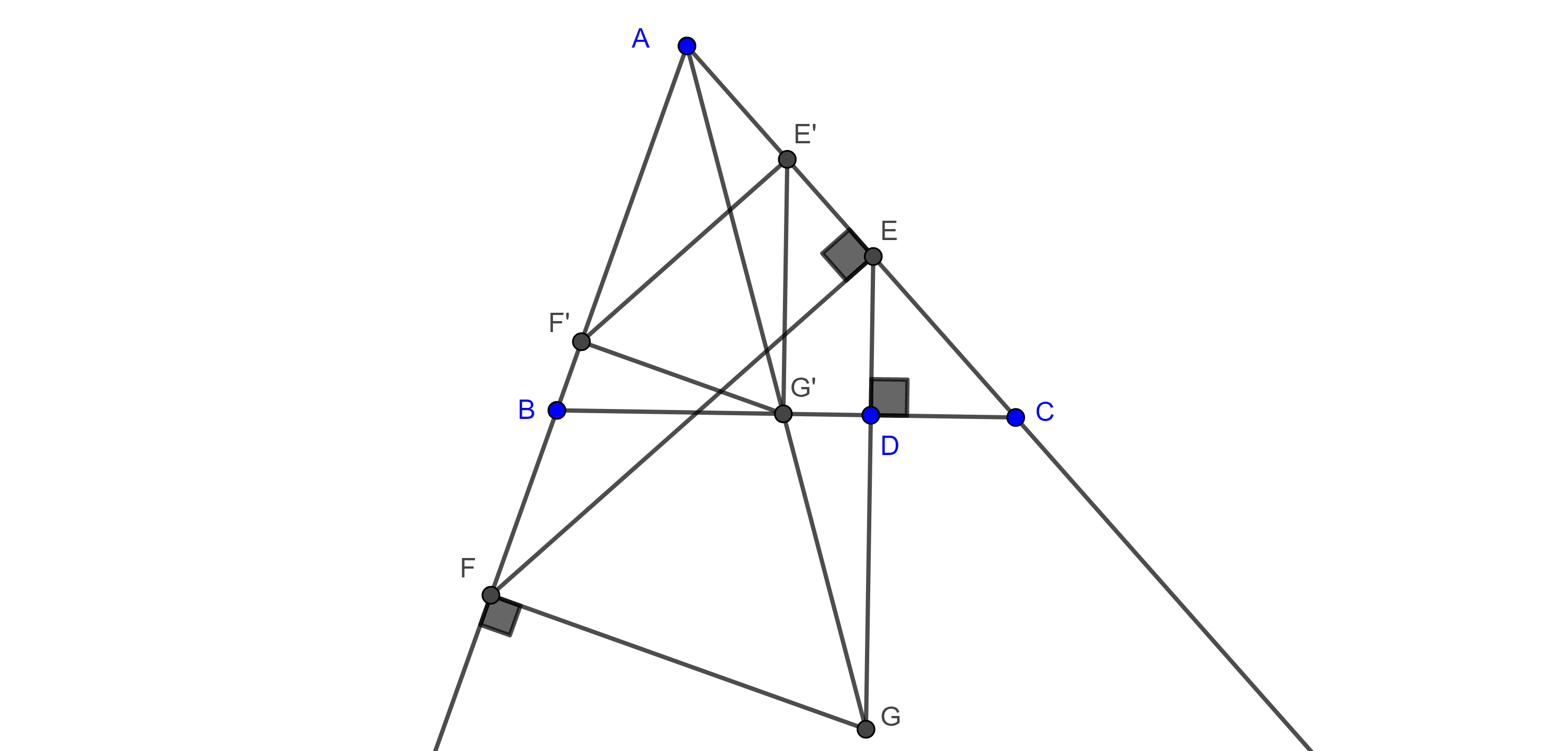
Corolario 2. Con las mismas condiciones y notación del teorema anterior, sea $H \in AC$ el pie de la altura por $B$, y sea $M$ el punto medio de $BH$, entonces $EI$ y $I_bD$ concurren en $M$ (figura 6).
Demostración. Ya que $D’D \parallel BH$ entonces $\triangle EBH \sim \triangle ED’D$,
$\Rightarrow \dfrac{EB}{ED’} = \dfrac{EH}{ED}$.
Es decir, hay una homotecia con centro en $E$ que lleva a los puntos $D’$ y $D$ a los puntos $B$ y $H$ respectivamente, esto implica que el punto medio de $D’D$ es homólogo del punto medio de $BH$.
Por lo tanto, $E$, $I$ y $M$ son colineales.
Por otra parte, consideremos la homotecia con centro en $B$ que lleva a $(I, r)$ en $(I_b, r_b)$ y sea $E’ \in (I_b, r_b)$ el punto homólogo de $D \in (I, r)$.
Como $(D, E’)$ y $(D’, E)$ son pares de puntos homólogos bajo la misma homotecia, entonces $DD’ \parallel E’E$ pero $DD’ \parallel HB$ $\Rightarrow E’E \parallel HB$.
Entonces $\triangle DEE’ \sim \triangle DHB$.
$\Rightarrow \dfrac{DB}{DE’} = \dfrac{DH}{DE}$.
En consecuencia, existe una homotecia con centro en $D$, y $(E, H)$, $(E’, B)$ son pares de puntos homólogos, de esto de sigue que el punto medio de $EE’$ y el punto medio de $BH$ son puntos homólogos.
Ya que $E’E \perp AC$, entonces es diámetro de $(I_b, r_b)$, por lo que $I_b$ es el punto medio de $E’E$ y así, $I_b$, $D$ y $M$ son colineales.
Por lo tanto, $EI$ y $I_bD$ concurren en $M$.
$\blacksquare$
Más adelante…
En la siguiente entrada hablaremos sobre la potencia de un punto con respecto a una circunferencia, es una herramienta útil que relaciona cualesquiera dos secantes a una circunferencia desde un punto en el plano, incluyendo el caso cuando una secante se vuelve tangente.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Un triángulo variable tiene un vértice sobre un punto fijo, un vértice sobre una recta fija y el triangulo permanece semejante a un triángulo dado, muestra que el tercer vértice describe una línea recta.
- Considera dos circunferencias que se intersecan, por uno de los puntos de intersección traza una recta que forme una cuerda en cada circunferencia y tal que la razón entre sus longitudes sea igual a una razón dada.
- Construye un triángulo semejante a un triángulo dado, de tal forma que un vértice sea un punto dado y los otros dos vértices estén sobre dos circunferencias dadas.
- Construye un triangulo $\triangle ABC$ dado su incentro, el punto medio del lado $BC$ y el pie de la altura por $A$.
- Lema de Arquímedes. Sea $\Gamma_2$ una circunferencia internamente tangente a una circunferencia $\Gamma_1$ en un punto $H$, considera $AB$, una cuerda de $\Gamma_1$ que es tangente a $\Gamma_2$ en $P$, sea $Q$ el punto medio del arco $\overset{\LARGE{\frown}}{AB}$ (figura 7), muestra que:
$i)$ $Q$, $P$ y $H$ son colineales,
$ii)$ $QP \times QH = QB^2$.
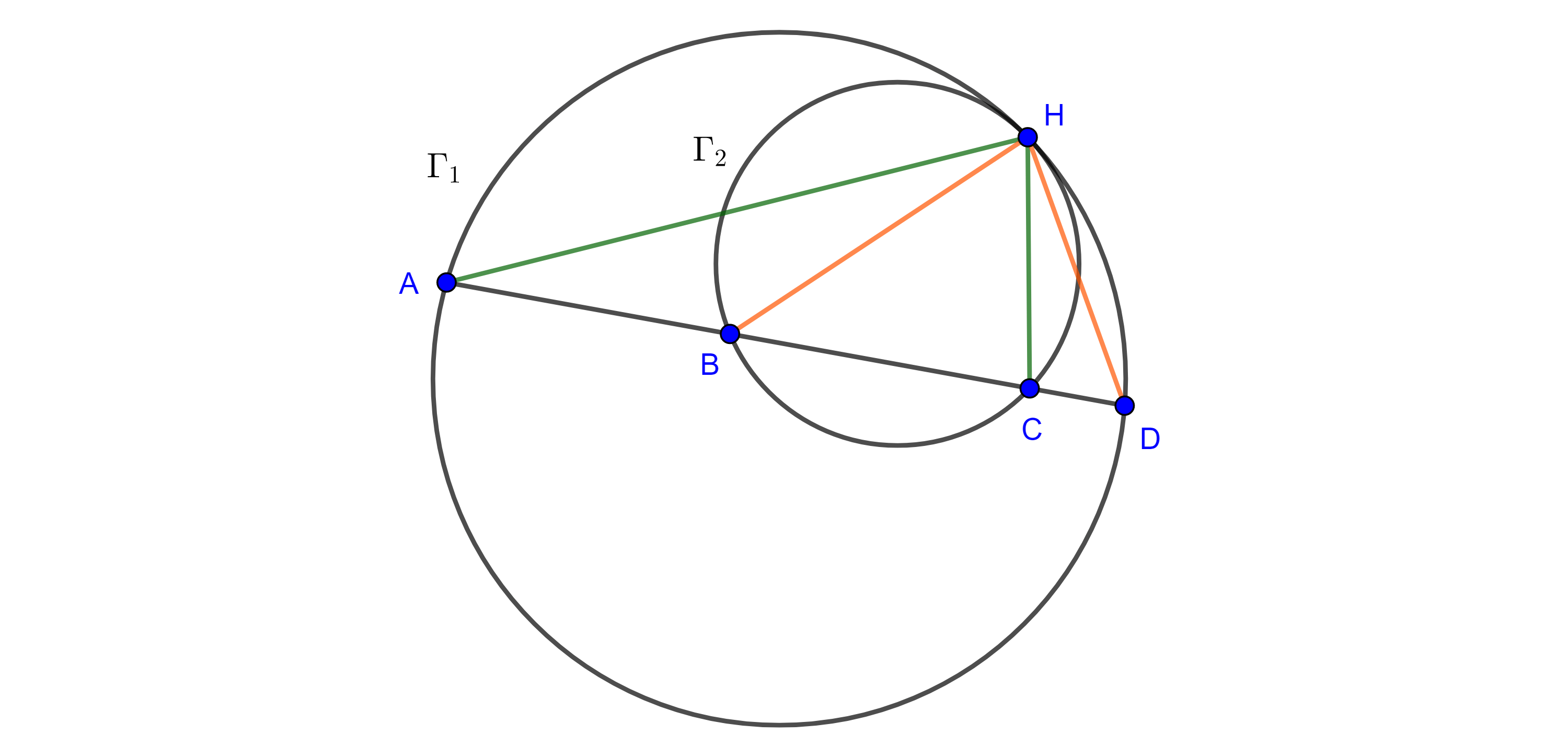
- Sea $\Gamma_2$ una circunferencia internamente tangente a una circunferencia $\Gamma_1$ en un punto $H$, considera una secante a ambas circunferencias en $A$, $B$, $C$ y $D$ (figura 8), prueba que $\angle AHC = \angle BHD$.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curso: Homotecia.
- Siguiente entrada del curso: Potencia de un punto.
- Otros cursos.
Fuentes
- Altshiller, N., College Geometry. New York: Dover, 2007, pp 46-51.
- Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 199-208.
- Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 109-114.
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»