Archivo de la etiqueta: funciones inversas

Cálculo Diferencial e Integral I: Funciones trigonométricas (Parte 2)

Por Karen González Cárdenas

Deja un comentario

Introducción


Ahora que hemos comenzado a revisar las funciones trigonométricas de seno y coseno, en esta entrada veremos las funciones tangente, cotangente, secante y cosecante. De igual manera, revisaremos las funciones inversas y su representación gráfica.

Hablemos de la tangente y la cotangente

Recordemos de la entrada anterior las definiciones:

\begin{align*}
tan(\theta)&=\frac{sen(\theta)}{cos(\theta)} & cot(\theta)&=\frac{cos(\theta)}{sen(\theta)}
\end{align*}

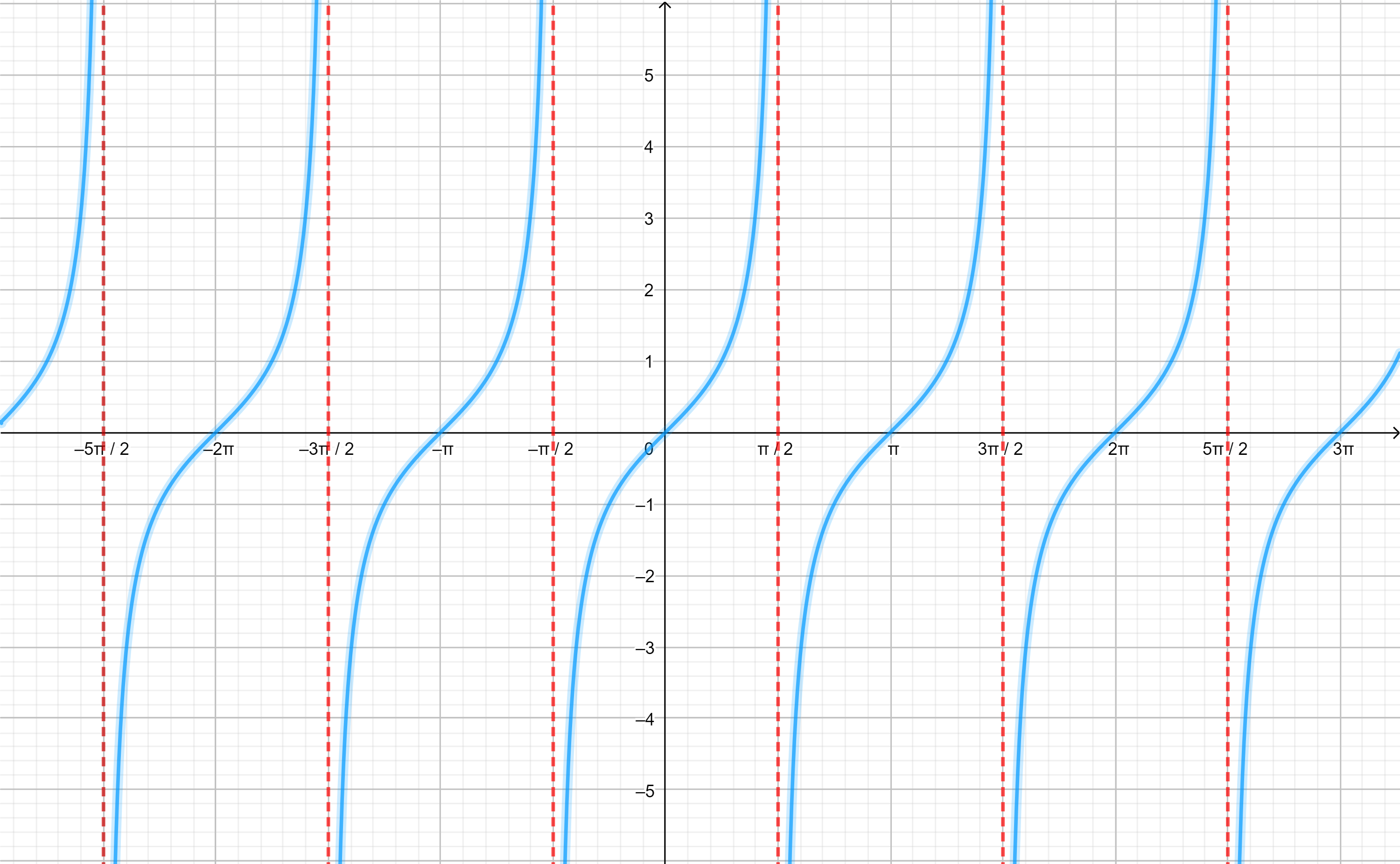
Para la función tangente tenemos que su gráfica se vería como:

Observación: La tangente presenta asíntotas en los valores $x=\frac{k \pi}{2}$ con $k \in \mathbb{Z}$.

Y su rama principal la consideramos definida en el dominio:
$$tan: \left(-\frac{\pi}{2}, \frac{\pi}{2} \right) \rightarrow \r$$

Y para la función cotangente su gráfica sería:

Observación: La cotangente presenta asíntotas en los valores $x=k \pi$ con $k \in \mathbb{Z}$.

Para esta función consideraremos como su rama principal en el siguiente dominio:
$$cot: (0,\pi) \rightarrow \r$$.

Ahora la secante y la cosecante

Ya vimos que están definidas como:
\begin{align*}
sec(\theta)&= \frac{1}{cos(\theta)} & csc(\theta)&= \frac{1}{sen(\theta)}.
\end{align*}

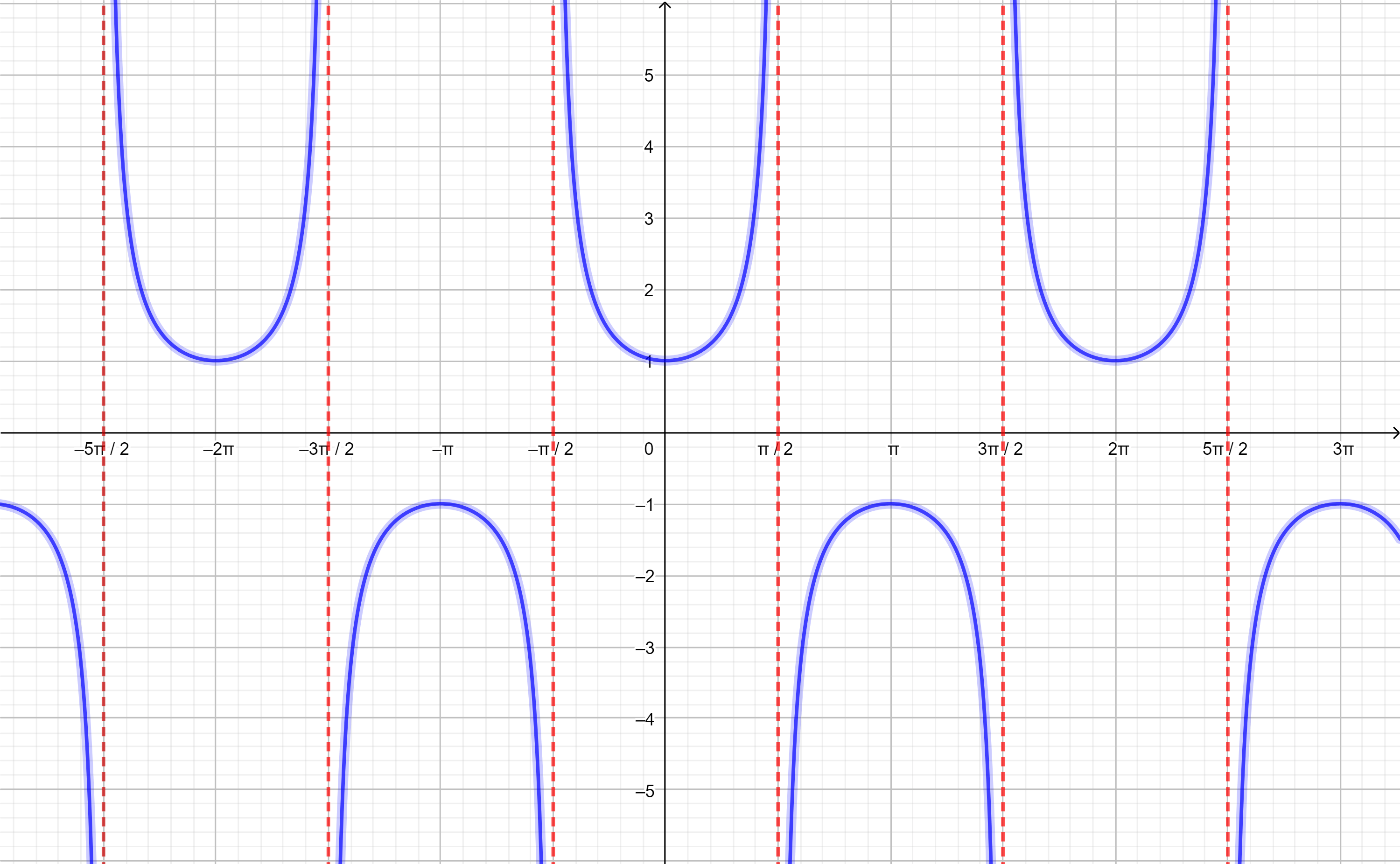
Comencemos con la gráfica para la función secante:

Observación: La secante presenta asíntotas en los valores $x=\frac{k \pi}{2}$ con $k \in \mathbb{Z}$.

Notemos que esta función se encuentra definida sobre cada cresta y por debajo de cada valle de la función $cos(\theta)$:

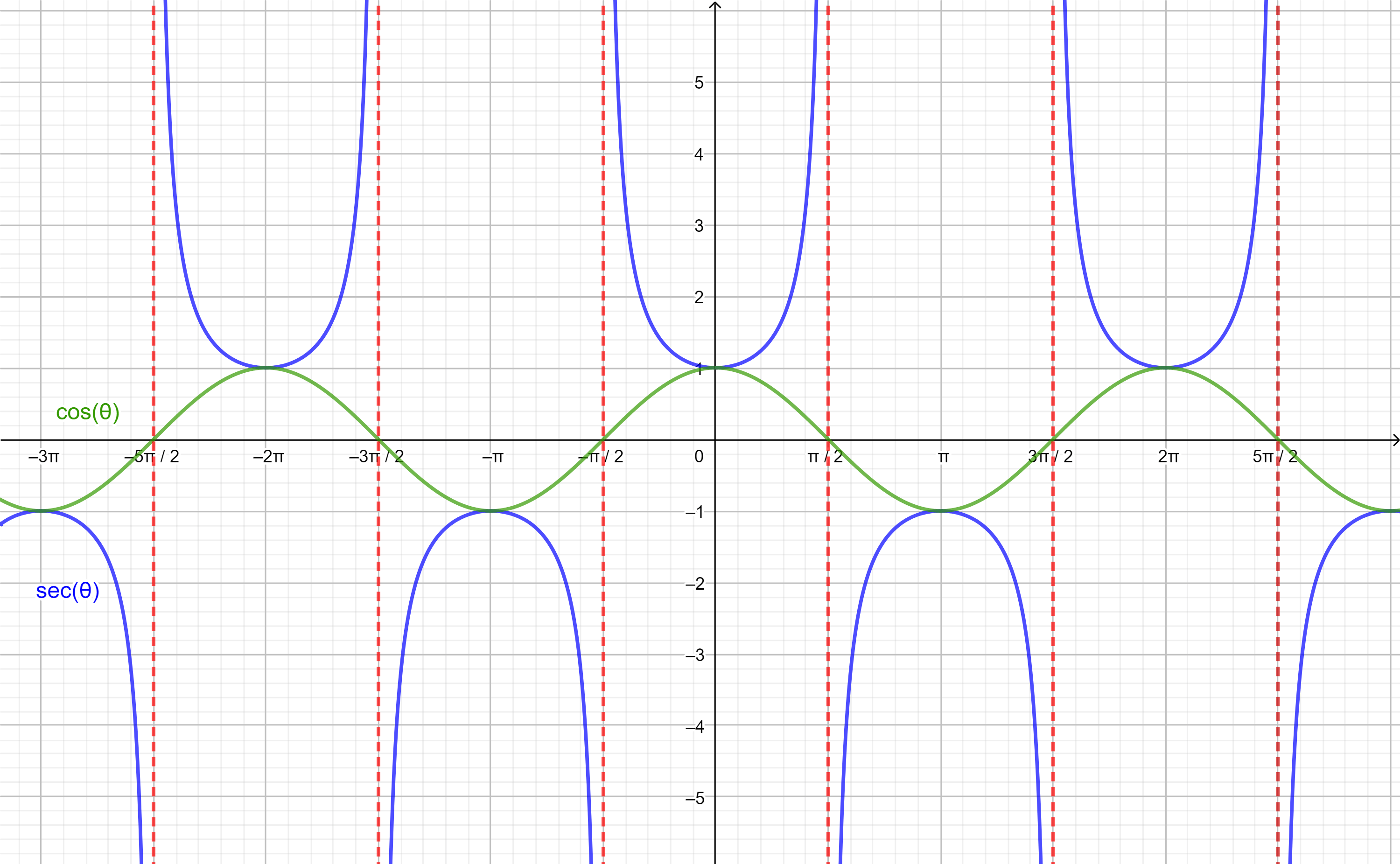
Tomaremos como domino donde la función es invertible a:
$$D= \left[0, \frac{\pi}{2} \right) \cup \left(\frac{\pi}{2},\pi \right].$$

Para la función cosecante vemos que se encuentra definida sobre cada cresta y por debajo de cada valle de la función $sen(\theta)$:

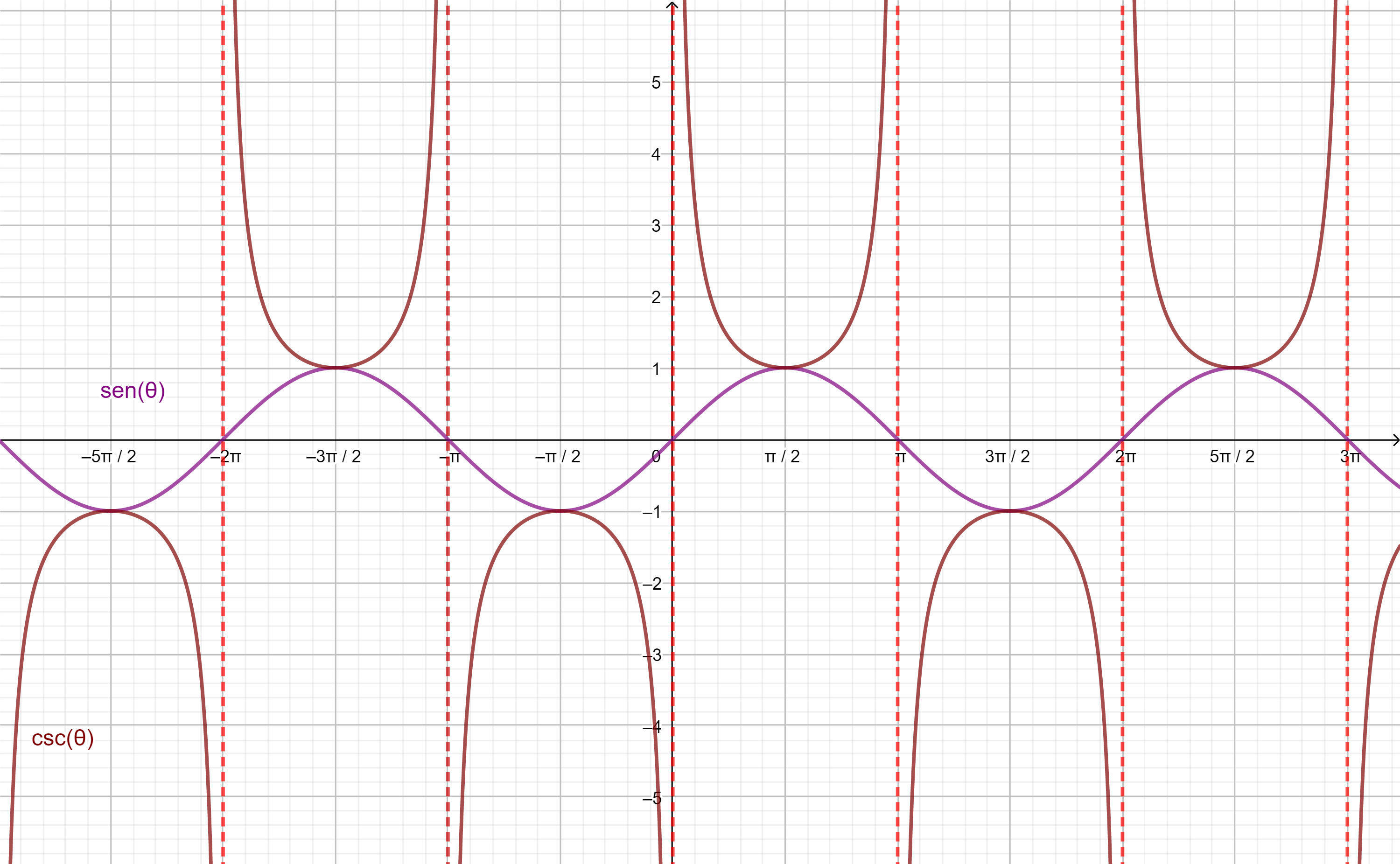
Observación: La cosecante presenta asíntotas en los valores $x=k \pi$ con $k \in \mathbb{Z}$.

Para esta función consideraremos al dominio donde es invertible a:
$$D= \left[-\frac{\pi}{2}, 0 \right) \cup \left(0, \frac{\pi}{2} \right].$$

¿Quiénes son las funciones inversas?

Para poder visualizar las gráficas de cada una de las funciones trigonométricas utilizaremos el método descrito previamente de reflejar la gráfica de la función respecto de la función identidad en el dominio donde es biyectiva o invertible.

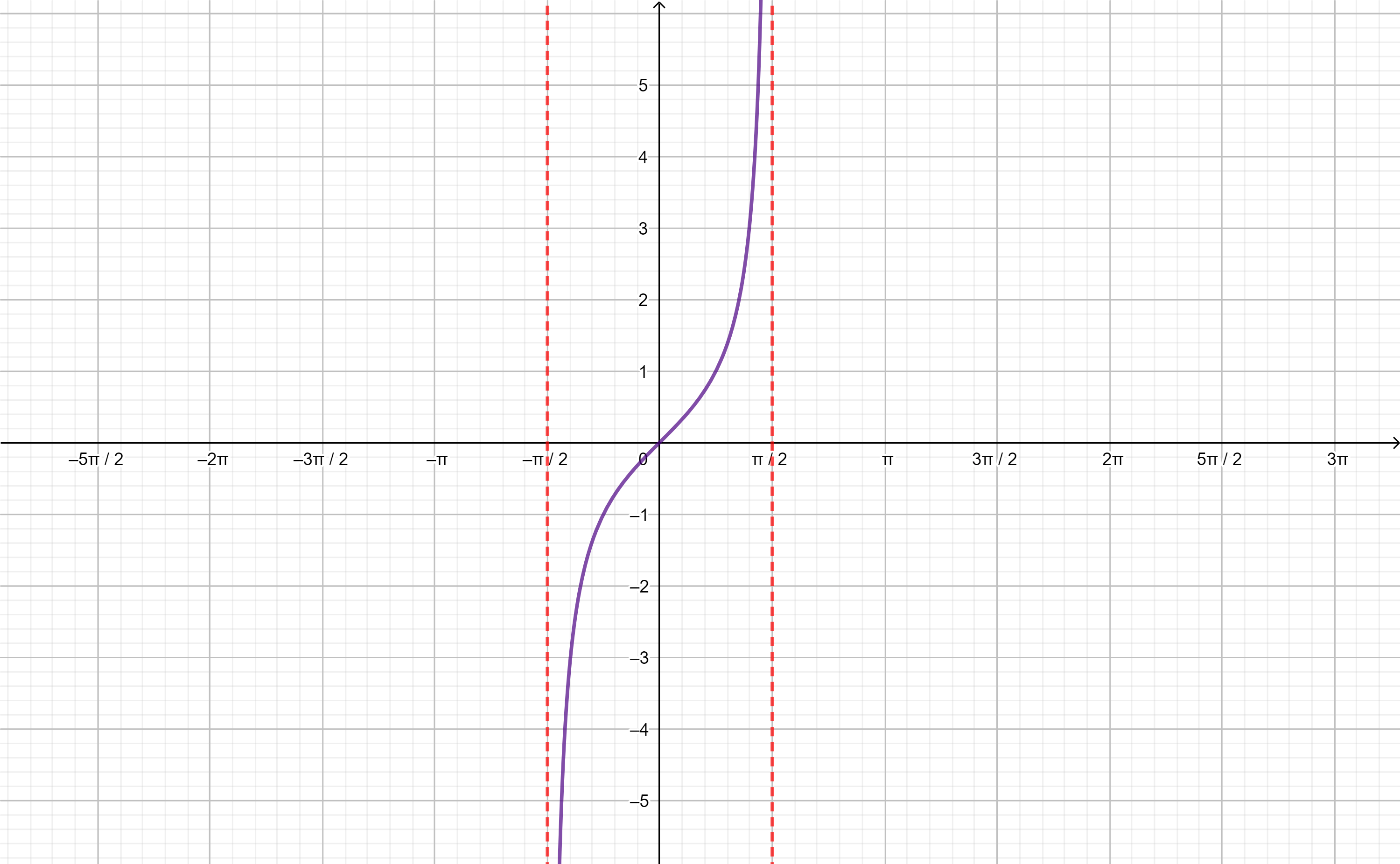
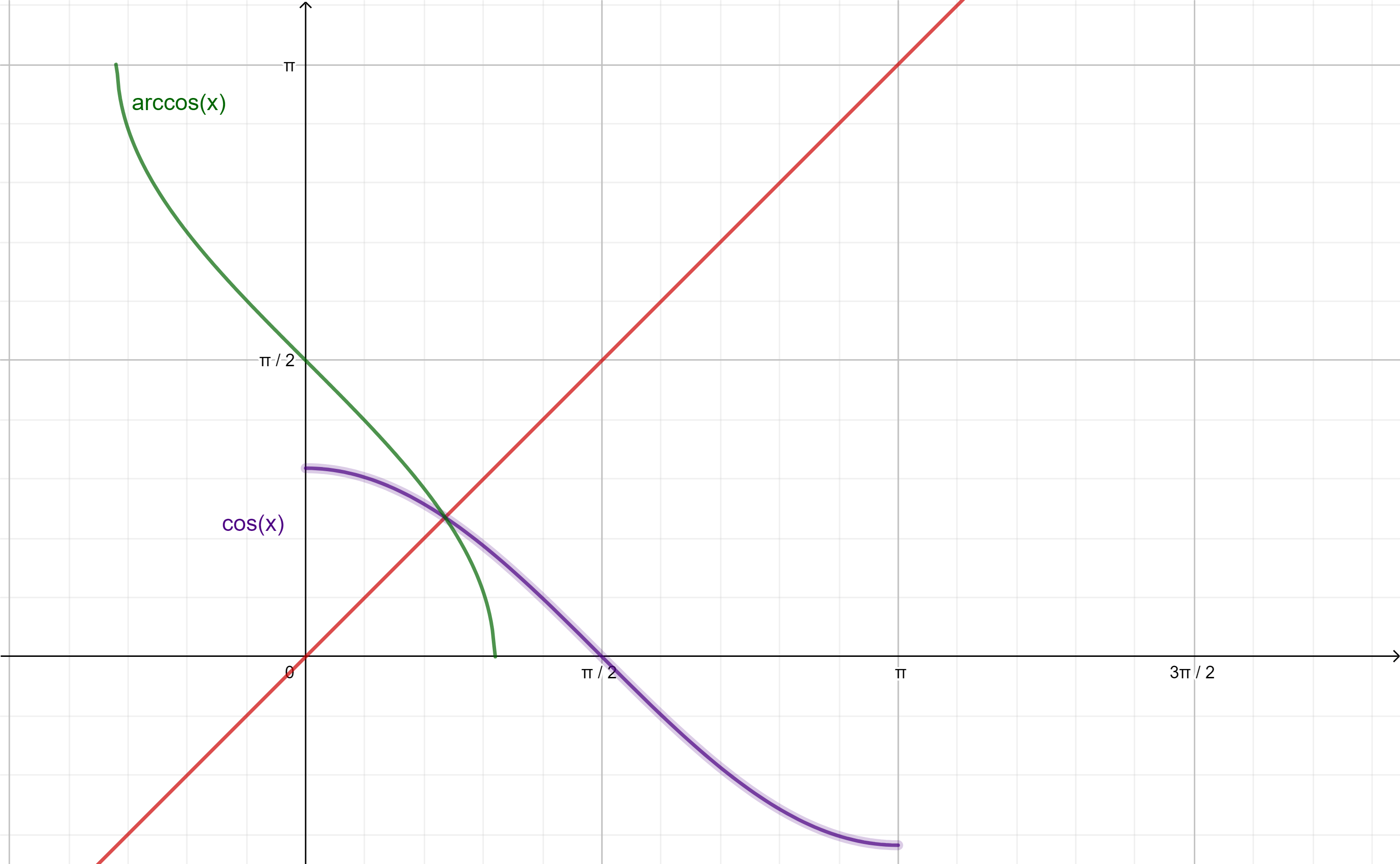
Comenzaremos con la inversa de la función $f(x)=sen(x)$ en el dominio $D_{f}=\left[ -\frac{\pi}{2}, \frac{\pi}{2} \right]$:

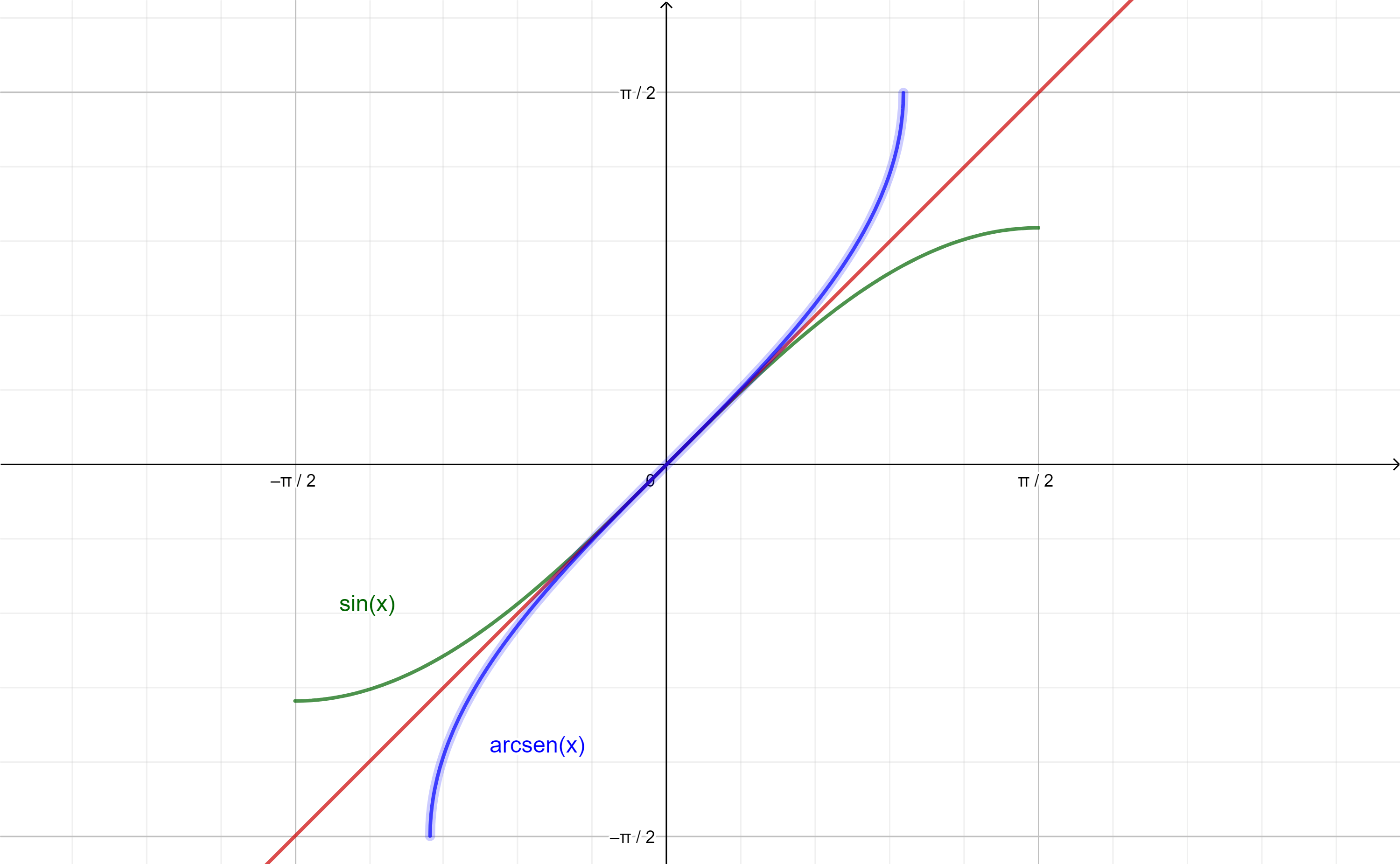
A $f^{-1}(x)$ la llamaremos arcoseno de $x$:
$$f^{-1}(x)=arcsen(x),$$
geométricamente esta función nos da el arco cuyo seno es $x$ valor.

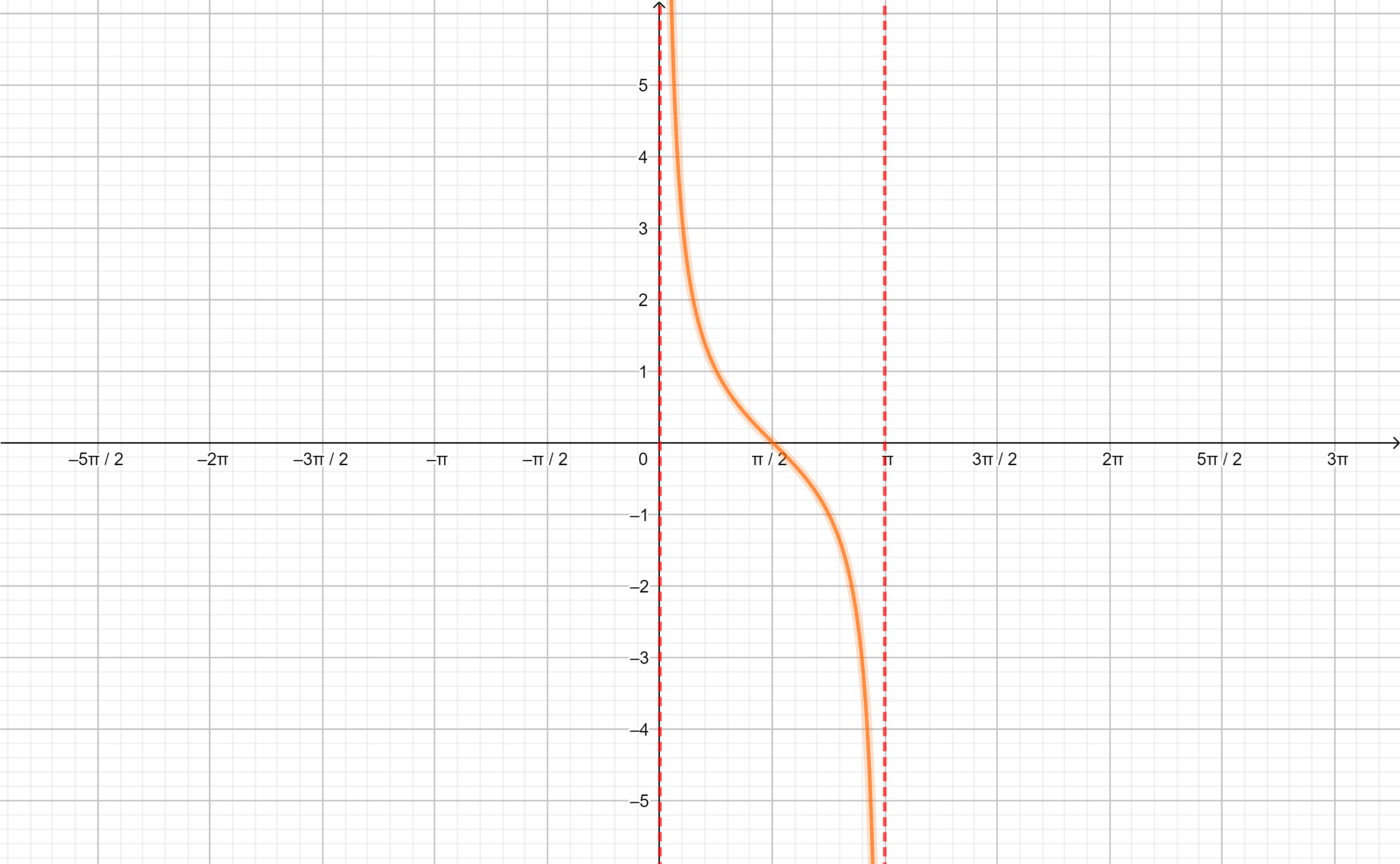
Procederemos de la misma manera con $g(x)=cos(x)$ en el dominio $D_{g}=[0,\pi]$:

Ahora a $g^{-1}$ la llamaremos arcocoseno de $x$:
$$g^{-1}(x)=arccos(x)$$
y su interpretación geométrica sería el arco cuyo coseno es el valor $x$.

Dejaremos como ejercicio de Tarea moral realizar la gráfica para la función inversa de $h(x)= tan(x)$ en el dominio $D_{h}= \left(-\frac{\pi}{2}, \frac{\pi}{2} \right)$:
$$h^{-1}(x)= arctan(x),$$
la función arcotangente nos da el arco cuya tangente es el valor $x$.

Más adelante

En la siguiente entrada veremos al conjunto de funciones exponenciales y logarítmicas, sus representaciones gráficas, la relación que existe entre ellas y algunos resultados que cumplen, como las leyes de los exponentes y las leyes de los logaritmos.

Tarea moral

  • Obtener la gráfica de las siguientes funciones:
    • $f(x)=-tan(x)$
    • $f(x)=-2sec(x)+1$
    • $f(x)=arctan(x)$
    • $f(x)=3-csc(x)$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»