Introducción

En la entrada anterior definimos qué es una elipse, hablamos de una técnica para trazar una y cómo esta técnica, nos conduce naturalmente a su definición analítica: una elipse es la curva que define al conjunto de puntos que cumplen que la suma a dos puntos distintos llamados focos es constante. Finalmente vimos cómo escribir la ecuación canónica de la elipse; a partir de esta ecuación canónica podemos leer toda su información geométrica.

Ahora, para finalizar nuestro estudio de las elipses, vamos a hablar de sus elementos, propiedades focales y sus propiedades métricas. Verás cómo algunos problemas de aplicación motivan el estudio formal de estas propiedades y extenderemos algunas de ellas para el estudio de las cónicas que nos faltan. Sin más preámbulo, abordaremos el tema.

Elementos de una elipse

En la entrada anterior hicimos mención a algunos de los elementos que componen una elipse. Como mencionamos, a partir de la ecuación canónica puedes leer directamente información como el eje menor y el eje mayor; conociendo estos dos ejes, puedes deducir cuáles son sus vértices y sus focos. Haciendo más cuentas puedes deducir cuál es su lado recto y directrices.

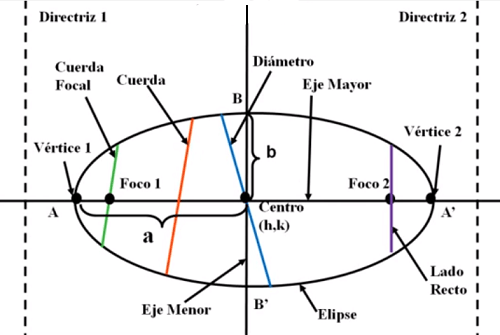
En la siguiente figura puedes observar un diagrama que muestra todos los elementos de la elipse y en la siguiente tabla puedes ver qué relación guardan unos con otros. Es importante que sepamos extraer toda la información geométrica que nos sea posible cuando se nos presente una ecuación en su forma canónica.

Elemento dentro de la elipse canónica	Expresión analítica
Longitud del eje mayor	$$2a$$
Coordenadas de los vértices	$$(\pm a,0)$$
Longitud del eje menor	$$2b$$
Coordenadas de los co-vértices	$$(0,\pm b)$$
Coordenadas de los focos	$(\pm c,0)\text{donde}{c}^2=a^2+b^2$
Excentricidad	$$\epsilon =\sqrt{\frac{a^2-b^2}{a^2}}=\sqrt{1-\frac{b^2}{a^2}}$$

Como puedes notar, la última fila se refiere a una propiedad de la elipse que no hemos discutido: la excentricidad. La excentricidad normalmente denotada como $ϵ$ es un parámetro que determina el grado de desviación de una sección cónica con respecto a una circunferencia. Pronto veremos que a partir de la excentricidad, podemos definir a las tres secciones cónicas como el lugar geométrico de los puntos $\mathbf{X}$ cuya razón de sus distancias a un foco $\mathbf{p}$ y a una recta $\ell$ es una constante fija. Profundizaremos en el estudio de la excentricidad a lo largo de esta unidad, por el momento fijemos la idea de que las elipses necesariamente deben tener una excentricidad menor que uno; es decir $ϵ<1$.

Otra observación importante: estas reglas se refieren a una elipse centrada en el origen que tiene una ecuación canónica $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$. No es el objetivo de esta unidad hablar de traslaciones y rotaciones; pero debes saber que si la elipse tiene el centro fuera del origen en un punto $(h,k)$, su ecuación se ve así: $\frac{x^2-h}{a^2}+\frac{y^2-k}{b^2}=1$. El estudio de elipses rotadas se aborda comúnmente en un segundo curso de geometría analítica.

Propiedad focal de la elipse

La propiedad focal de la elipse es es que cualquier fotón que sale de uno de los focos, se refleja dentro de la elipse para llegar al otro foco. Si no estás familiarizado con el fotón, imagina la siguiente situación: estás en un cuarto con paredes reflejantes y con forma elíptica; si tu te paras en uno de los focos del cuarto y apuntas con una linterna hacia algún punto en las paredes, el rayo de luz de tu linterna impactará directamente en el otro foco.

Existen dos formas de formalizar la propiedad que describimos en el párrafo anterior; la primera consiste en tomar el círculo de radio $2\mathbf{a}$ centrado en el foco $\mathbf{p}$ (este círculo contiene el otro foco $\mathbf{q}$, puesto que ahora $2a>d(p,q)$) y luego ver que para los puntos de este círculo, su mediatriz con $\mathbf{q}$ es tangente a la elipse $\mathcal{E}$. La segunda forma de resolver este problema nos va a permitir abordar el clásico «problema del bombero», entonces dejaremos el primero como tarea moral.

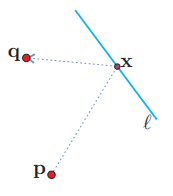
Para hablar del problema del bombero observa la siguiente figura, supongamos que un bombero está para en el punto $\mathbf{p}$ y hay un incendio en el punto $\mathbf{q}$. Pero tiene su cubeta vacía, y entonces tiene que pasar primero a llenarla a un río cuyo borde es la recta $\mathcal{l}$. El problema consiste en saber cuál es la trayectoria óptima que debe seguir el bombero. Es decir, ¿para cuál punto $x\in \mathcal{l}$? se tiene que $\mathrm{d}(\mathbf{p},\mathit{x})+\mathrm{d}(\mathit{x},\mathbf{q})$ es mínima.

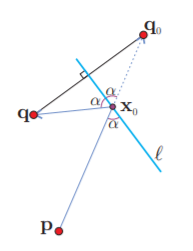
Nota cómo no hemos específicado de qué lado del río está el fuego; si estuviera del otro lado que el bombero, cualquier trayectoria al fuego tiene que pasar por $\mathcal{l}$ y entonces debe irse por la línea recta de $\mathbf{p}$ a $\mathbf{q}$ y tomar agua en ${\mathit{x}}_0=\ell \cap \overline{\mathbf{p}\mathbf{q}}$ (ver la siguiente figura). Entonces, si fuego y bombero están del mismo lado del río $\mathcal{l}$ podemos pensar en un «fuego virtual», que es el reflejado de $\mathbf{q}$ en $\mathcal{l}$, llamémosle ${\mathbf{q}}_0$, que cumple que $\mathrm{d}(\mathbf{x},\mathbf{q})=\mathrm{d}(\mathbf{x},{\mathbf{q}}_0)$ para todo $\mathbf{x}\in \mathcal{l}$, (para $\mathbf{q}$ y ${\mathbf{q}}_0$, \mathcal{l} es su mediatriz). La solución es, por el caso anterior, ${\mathbf{x}}_0=\ell \cap \overline{{\mathbf{p}\mathbf{q}}_0}$.

Pero observa cómo además de que el ángulo $\alpha$ con el que llega el bombero a $\mathcal{l}$ es igual al ángulo de «de reflexión» con el que sale corriendo al fuego (ya con la cubeta llena), e igual al ángulo con el que seguiría su trayecto al fuego virtual; y que esta propiedad determina el punto de mínimo recorrido ${\mathbf{x}}_0$; es fácil convencerse de que para cualquier otro punto de $\mathcal{l}$ los ángulos de llegada y de salida son distintos. Si los bomberos fueran fotones que salen de $\mathbf{p}$ y $\mathcal{l}$ es un espejo, el único que llega a $\mathbf{q}$ es el fotón de recorrido mínimo.

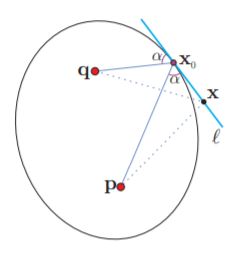
Para aterrizar nuestro problema del bombero al caso de las elipses, considera ahora que $\mathbf{p}$ y $\mathbf{q}$ son los focos de una elipse y ${\mathbf{x}}_0$ un punto en ella. Sea $\mathcal{l}$ la recta que pasa por ${\mathbf{x}}_0$ y bisecta (por fuera) los segmentos de $\mathbf{p}$ y $\mathbf{q}$ a ${\mathbf{x}}_0$. Por construcción, y considerando la solución al problema del bombero, cualquier otro punto $\mathbf{x}\in \mathcal{l}$ tiene mayor suma de distancias a los focos y por tanto está fuera de la elipse. Esto demuestra que $\mathcal{l}$ es la tangente a la elipse en el punto ${\mathbf{x}}_0$, y por lo tanto, queda demostrada la propiedad focal de la elipse.

Antes de dar por terminada esta sección, te invito a que experimentes con el siguiente recuadro interactivo de GeoGebra: en él podrás ver cómo funciona esta propiedad focal de las elipses para elipses de diferentes tamaños y posiciones. ¿Puedes ver qué pasa con esta propiedad para el caso degenerado de la elipse? ¿Qué pasa si los focos son el mismo punto?

Propiedades métricas de la elipse

Tocaremos brevemente el tema de las propiedades métricas de la elipse; lo haremos sólo superficialmente pues una demostración formal se escapa de lo que planeamos cubrir en este curso. Si no estás familiarizado con los términos que aparecen en esta sección, no te preocupes, enfócate en entender cómo se llegó a los resultados y tenlos como referencia por si los ocupas en algún otro curso un poco más enfocado a las aplicaciones de las elipses.

La primera de sus propiedades métricas que vamos a abordar es el área de la elipse: considera que esta propiedad se refiere a la elipse con ecuación:

$$\begin{array}{}\text{(1)}& \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\end{array}$$

La ecuación anterior, puede ser reescrita como

$$\begin{array}{}\text{(2)}& y(x)=b\sqrt{1-x^2/a^2}.\end{array}$$

Para toda $x\in [-a,a]$, esta curva es la mitad superior de la elipse. Entonces, el doble de la integral $y(x)$ sobre le intervalo $[-a,a]$ será el área de la elipse:

$$\begin{array}{}\text{(3)}& \begin{array}{rlr}{A}_{\text{ellipse }}& ={\int }_{-a}^{a}2b\sqrt{1-\frac{x^2}{a^2}}dx& =\frac{b}{a}{\int }_{-a}^{a}2\sqrt{a^2-x^2}dx.\end{array}\end{array}$$

La segunda integral es el área del círculo con radio $a$, la cual vale $\pi a^2$. Entonces,

$$\begin{array}{}\text{(4)}& A_{\text{ellipse }}=\frac{b}{a}\pi a^2=\pi ab.\end{array}$$

La circunferencia de una elipse, es decir, el análogo del perímetro para las circunferencias presenta un problema: ¡es bastante difícil de obtener! pues hay que calcular una integral que no puede ser evaluada en términos de funciones elementales. De momento, pondremos sólo la fórmula, pues es un resultado bastante útil. Si te interesa ver cómo se llegó a este resultado, puedes revisar la siguiente fuente.

$$\begin{array}{}\text{(5)}& C\approx \pi [3(a+b)-\sqrt{(3a+b)(a+3b)}]=\pi [3(a+b)-\sqrt{10ab+3(a^2+b^2)}]\end{array}$$

La última de estas propiedades métricas que veremos superficialmente será la curvatura; esto te podría resultar especialmente útil si por ejemplo quisieras calcular la curvatura de la trayectoria para una partícula que se mueve trazando una parábola. La curvatura para una elipse con ecuación canónica $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ será:

$$\begin{array}{}\text{(6)}& \kappa =\frac{1}{a^2{b}^2}{(\frac{x^2}{a^4}+\frac{y^2}{b^4})}^{-\frac{3}{2}}.\end{array}$$

Más adelante…

En esta entrada y en la anterior profundizamos en las propiedades de la elipse. Seguiremos nuestro estudio de las secciones cónicas definiendo a las hipérbolas, veremos que a pesar de ser figuras muy distintas, guardan una relación estrecha con los círculos y las elipses. Al igual que para las figuras que hemos visto hasta el momento, entenderemos cómo llegar a una expresión analítica y aprenderemos a leer toda la información geométrica que contiene.

Tarea moral

• Demuestra la propiedad focal de la elipse sin resolver el problema del bombero. Sugerencia. toma el círculo de radio $2\mathbf{a}$ centrado en un foco $\mathbf{p}$ y luego ve que para los puntos de este círculo, su mediatriz con $\mathbf{q}$ es tangente a una elipse.
• Halle la ecuación de la elipse con centro en el origen que satisface las condiciones dadas; construya la curva:

1. La longitud del eje mayor es $10$ y l del eje menor $8$; los focos están sobre el eje $y$.
2. El eje menor mide $10$ y un vértice es $(6,0)$.
3. El lado recto mide $\frac{32}{7}$ y uno de los extremos del eje menor está en $(4,0)$.

• Obten el área de la elipse que tiene la siguiente ecuación:

$$\frac{x^2}{16}+\frac{y^2}{25}=1$$

• Obtenga una aproximación del perímetro de la siguiente elipse:

$$\frac{x^2}{25}+\frac{y^2}{225}=1$$

• Obtenga la curvatura de la siguiente elipse en el punto $(3,2)$:

$$\frac{x^2}{16}+\frac{y^2}{9}=1$$

Entradas relacionadas

• Ir a Geometría Analítica I
• Entrada anterior del curso: Elipses
• Siguiente entrada del curso: Problemas con elipses