$ \textit{ MATERIAL EN REVISIÓN}$
Introducción
Ya que hemos visto cómo son las bolas abiertas en diferentes métricas, procederemos a analizar cómo son cuando las comparamos con un conjunto $A \subset X$. Como recurso, usaremos imágenes representativas con la intención de ayudar en la abstracción de los conceptos que a continuación se anuncian. Aunque las bolas no necesariamente se representan siempre como circunferencias (métrica del taxista), o como objetos con bordes punteados (como el segmento vertical que forma parte de la bola abierta en la métrica del ascensor), para fines gráficos rescataremos la idea de usar líneas punteadas para hacer alusión al «borde» de una bola abierta, sugiriendo que son puntos en el conjunto $X$ que no están en ella. Por el contrario, representaremos con lineas continuas a los puntos que sí formen parte de un conjunto dado.
Unas breves comparaciones entre subconjuntos y puntos
Para iniciar, pensemos en un espacio métrico $(X,d)$:
Y en un conjunto $A$ contenido en $X$:
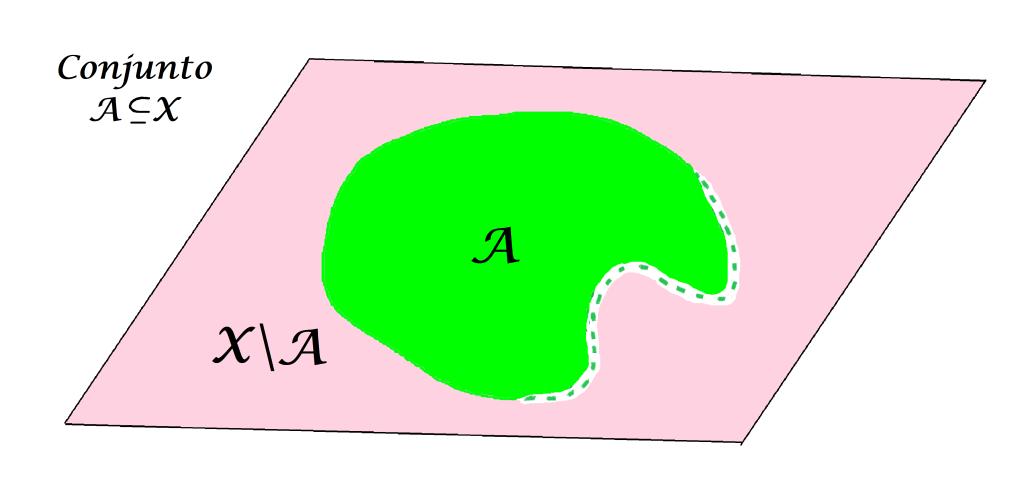
Identifiquemos puntos arbitrarios en $X$:
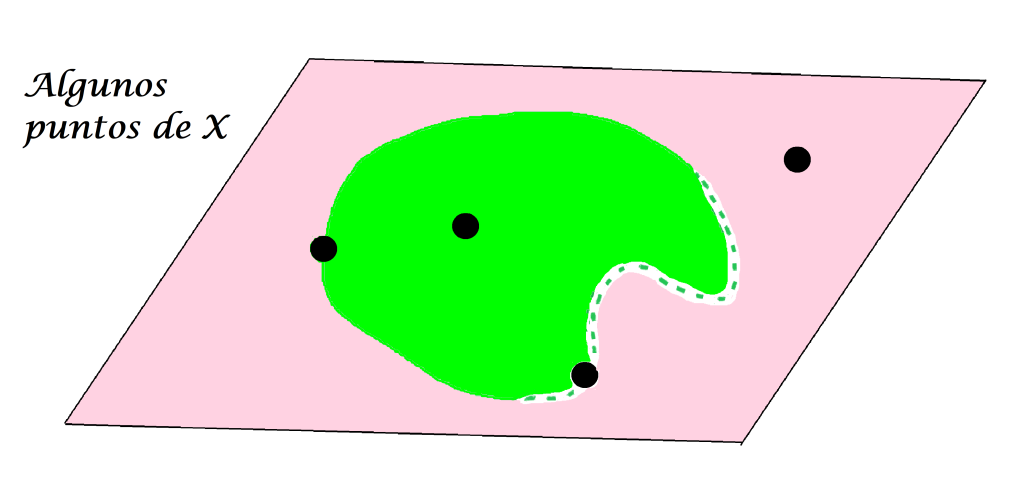
Entonces un punto $x \in X$ puede pertenecer o no al conjunto $A$.
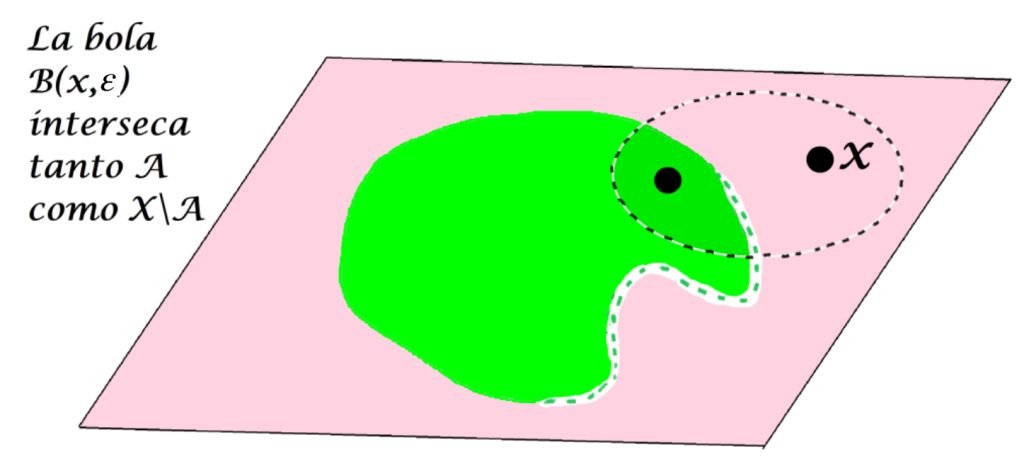
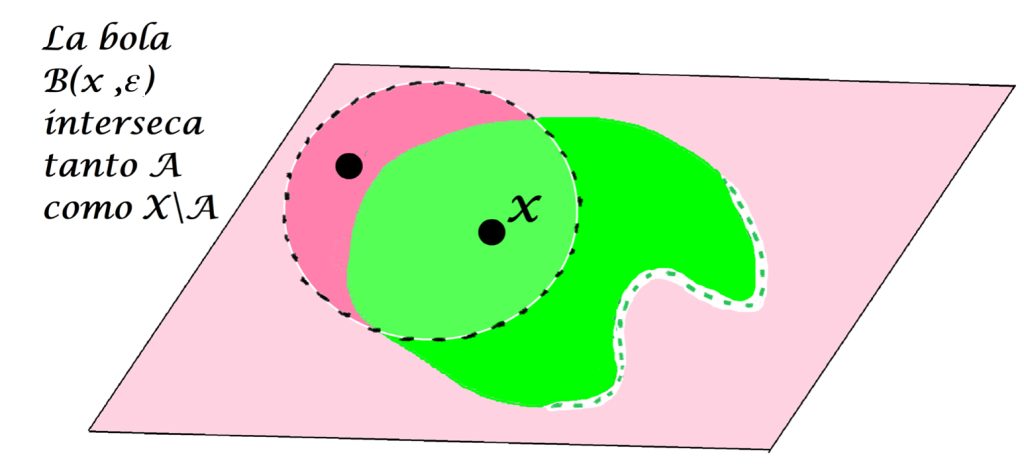
Si $x \in A$, entonces una bola abierta con centro en $x$ podría tener puntos tanto en $A$ como en $X \setminus A$.
¿Puede haber una bola con centro en un punto en $A$ que esté totalmente contenida en el conjunto $X \setminus A$?
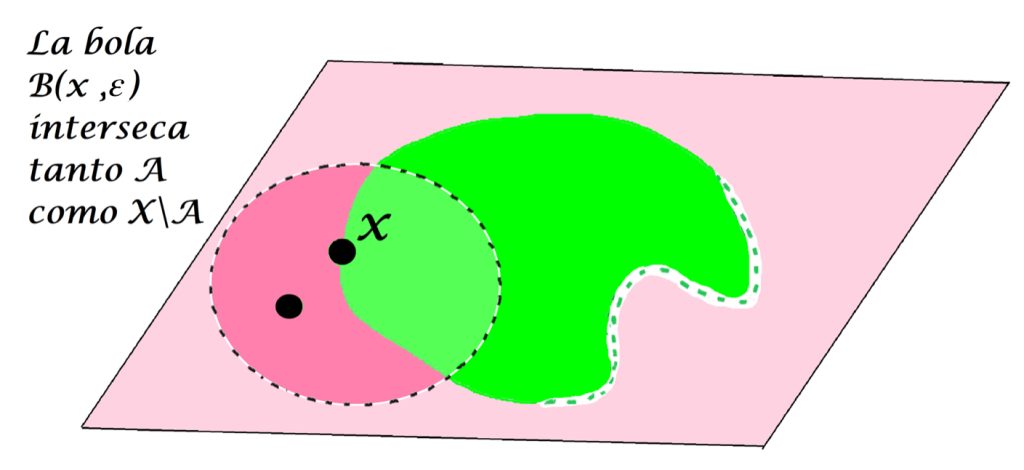
Por otro lado, si consideramos ahora $x \notin A$ , una bola abierta con centro en $x$ podría tener puntos tanto en $A$ como en $X \setminus A$.
O bien, puede solo tener puntos en $X \setminus A$
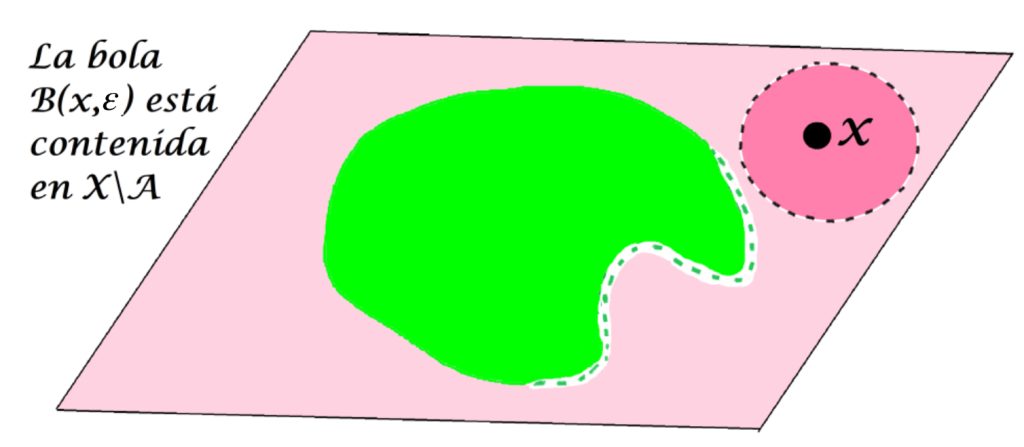
¿Es posible que una bola con centro en un punto en $X \setminus A$ esté totalmente contenida en $A$?.
Habiendo hecho estos comentarios generales, asignemos términos a los puntos de $X$ según las condiciones que cumplan las bolas abiertas asociadas.
Conceptos topológicos en un espacio métrico
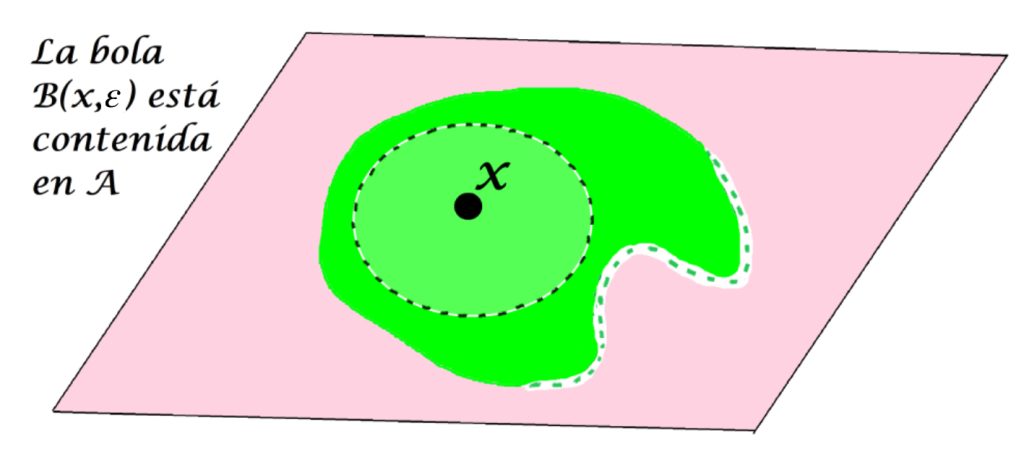
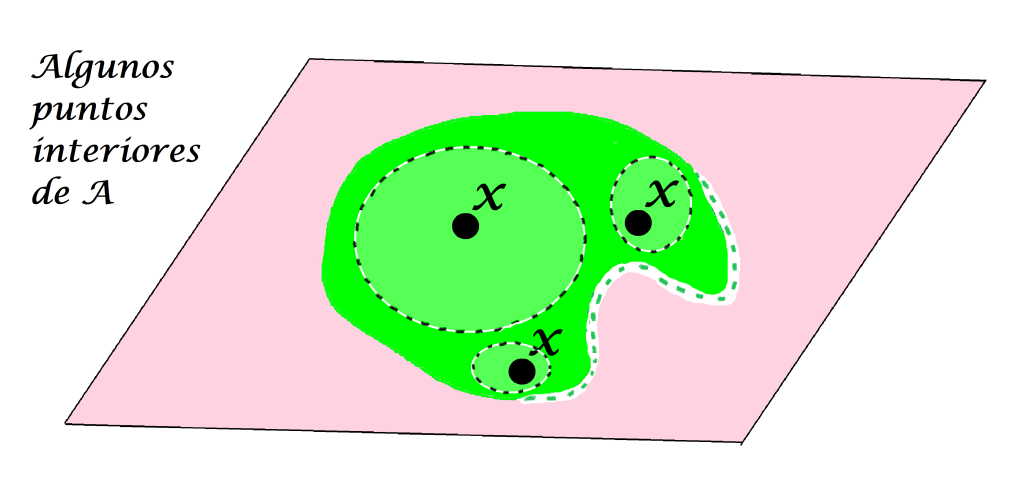
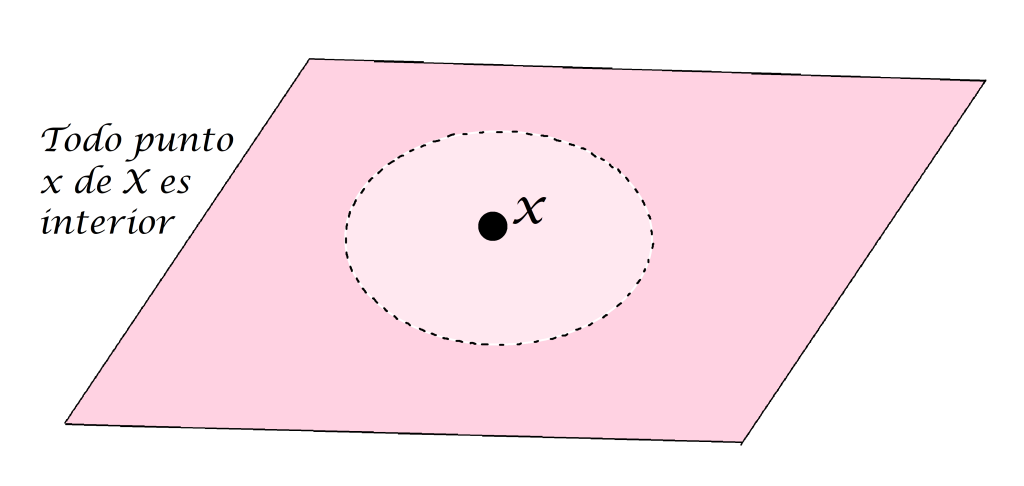
Definición. Punto interior de un conjunto. Sea $A$ un subconjunto del espacio métrico $(X,d)$ y sea $x \in X$. Decimos que $x$ es punto interior de $A$ en $(X,d)$ si existe $\varepsilon > 0$ tal que $B(x,\varepsilon) \subset A$.
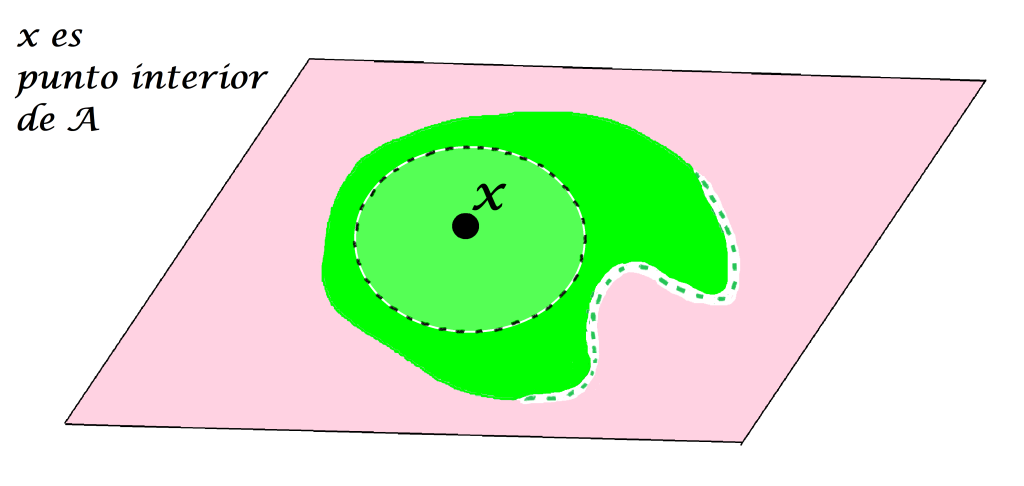
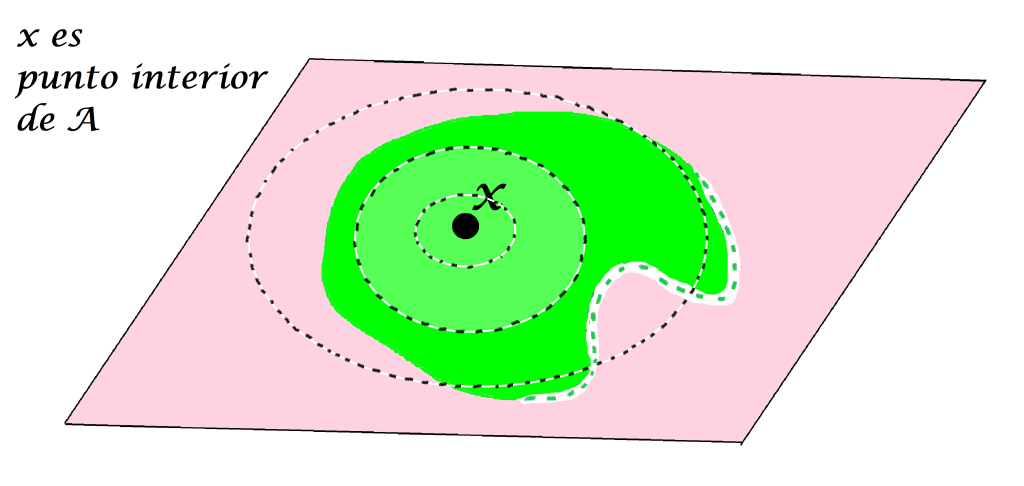
Aunque $x$ pueda tener alguna bola abierta que no esté «totalmente» contenida en $A$, basta con que exista una que sí lo esté para que a $x$ se le considere un punto interior.
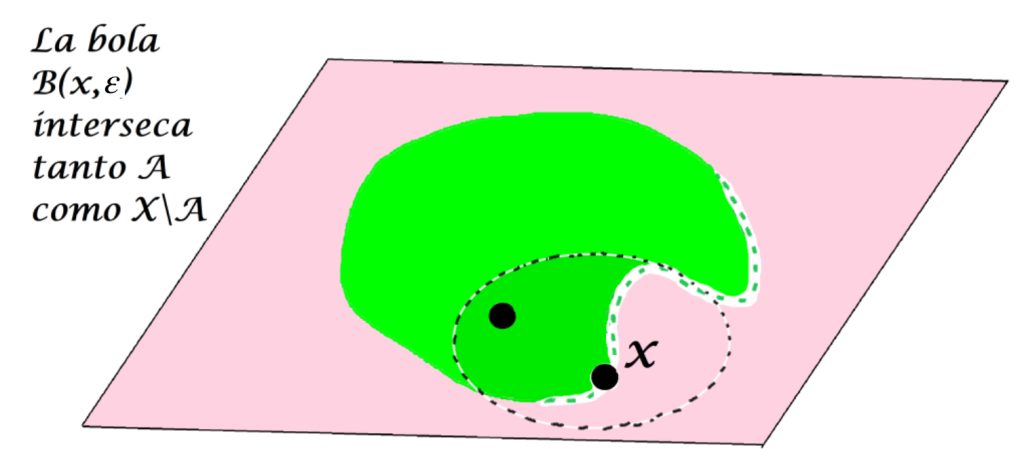
De acuerdo con la definición, un punto $x \in X$ no será punto interior de $A$ cuando para todo $ \varepsilon >0, B(x,\varepsilon)$ tiene puntos en $X \setminus A$. Los siguientes esquemas muestran puntos que no son puntos interiores del conjunto $A$ (tal vez sí lo sean de otro conjunto).
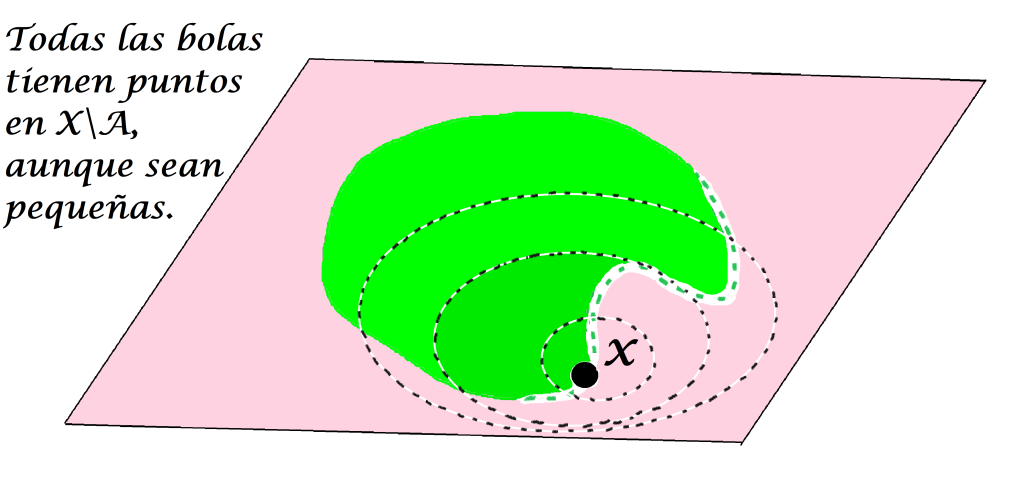
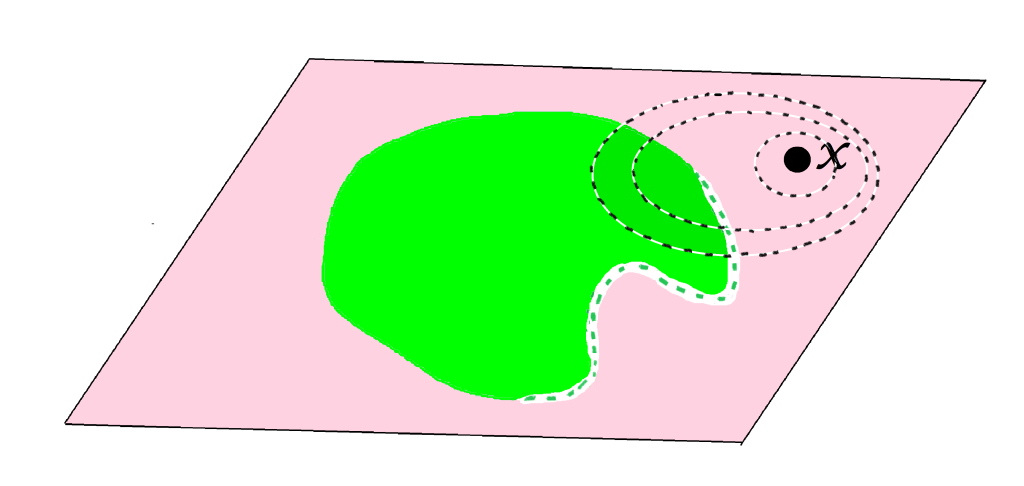
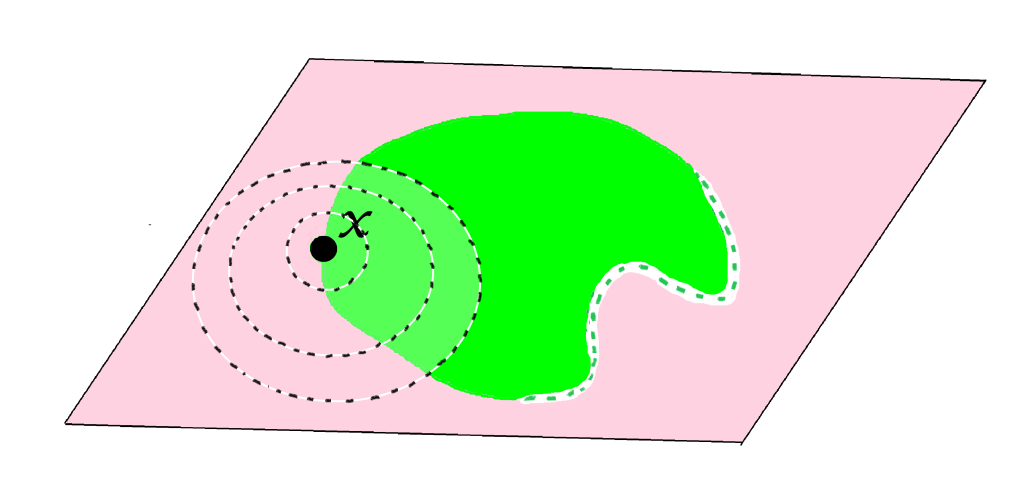
Definición. Interior de un conjunto. El conjunto formado por todos los puntos interiores de $A$ se denomina interior de $A$ en $(X,d)$ y se denota como:
$$Int (A) := \{x \in X|x \text{ es punto interior de A}\}$$
El conjunto $Int(A)$ se representa de la siguiente manera:
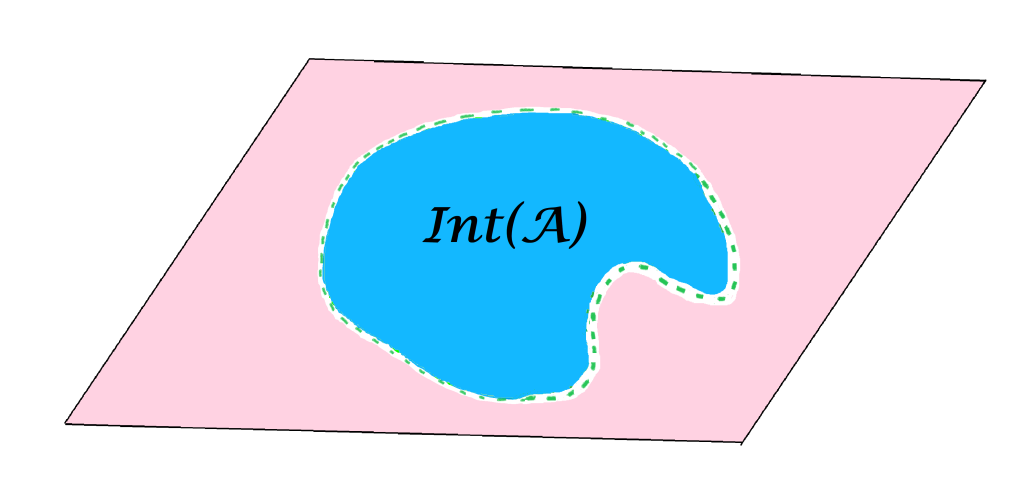
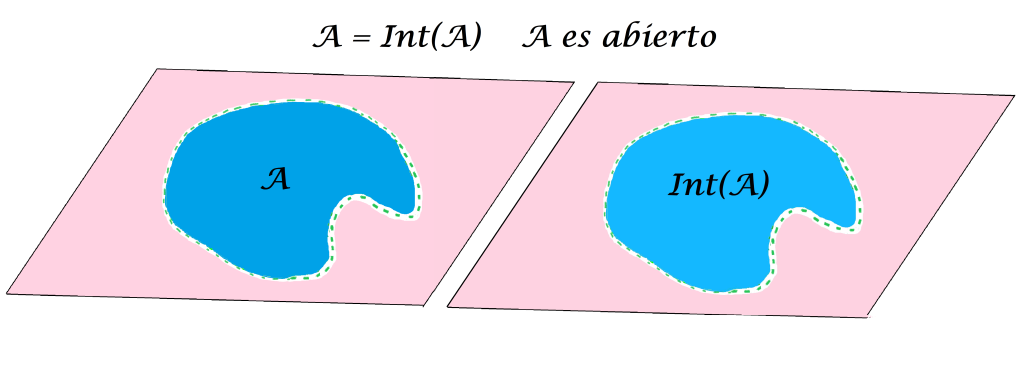
Definición. Conjunto abierto. Diremos que $A \subset X$ es un conjunto abierto en $(X,d)$ si $A=Int(A)$.
Nota que en la definición de punto interior, no hemos pedido, explícitamente, que el punto en cuestión pertenezca a $A,$ pero si pruebas que para todo $A \subset X$ se cumple que $Int(A) \subset A$ notarás que un conjunto $A$ es abierto cuando todos sus puntos son puntos interiores, es decir, cuando también $A \subset Int(A)$. El conjunto $A$ que estamos considerando en nuestros dibujos no es abierto, pues tiene puntos que no son puntos interiores.
Pero si tomamos un conjunto $A$ de la siguiente forma, sí coincide con su interior y por lo tanto, es abierto.
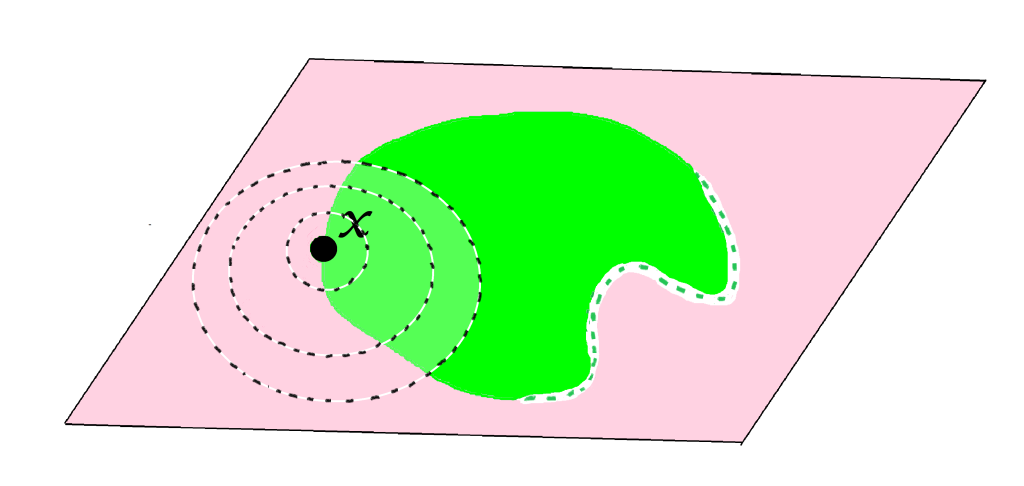
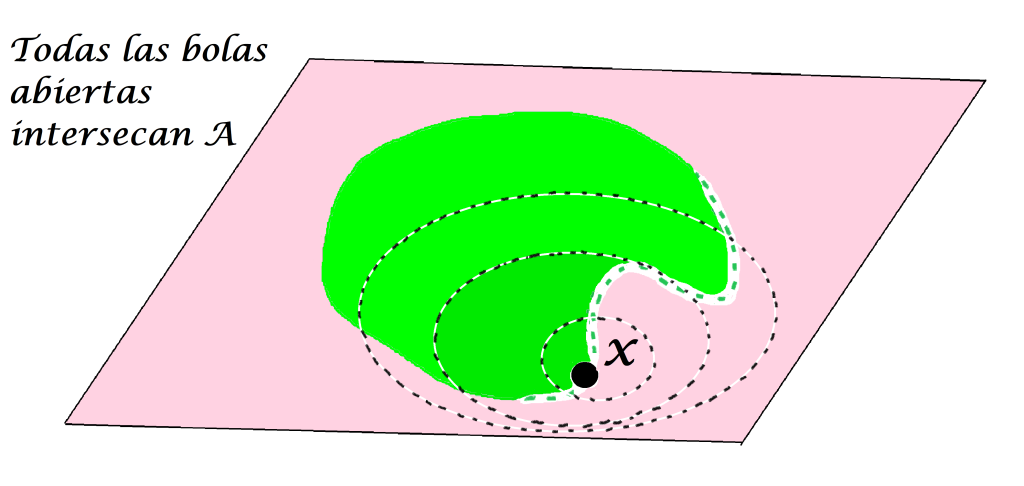
Definición. Punto de contacto o punto de adherencia. Sea $A$ un subconjunto del espacio métrico $(X,d)$ y sea $x \in X$. Se dice que $x$ es punto de contacto (o de adherencia) de $A$ en $(X,d)$ si para todo $\varepsilon >0$ se cumple que $B(x,\varepsilon) \cap A \neq \emptyset$.
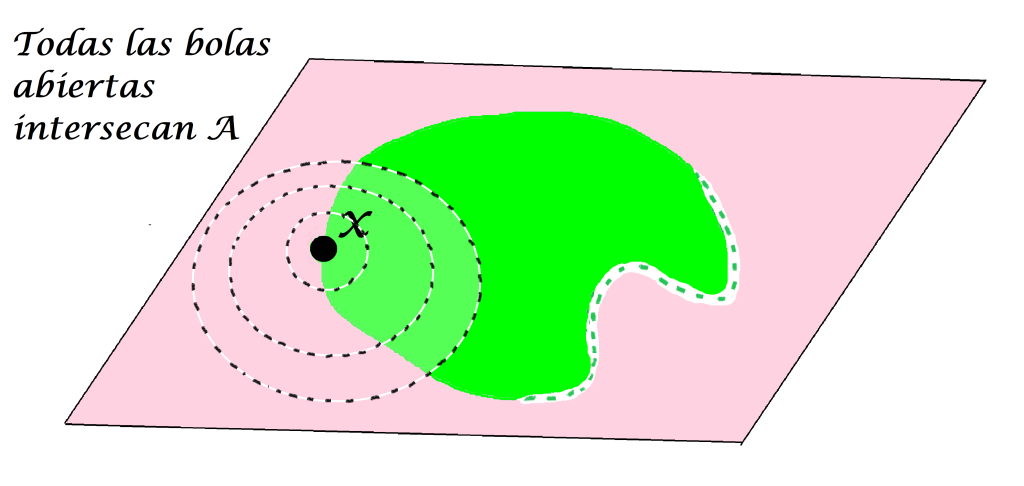
Incluso un punto que no esté en $A$ podría ser punto de contacto de $A$.
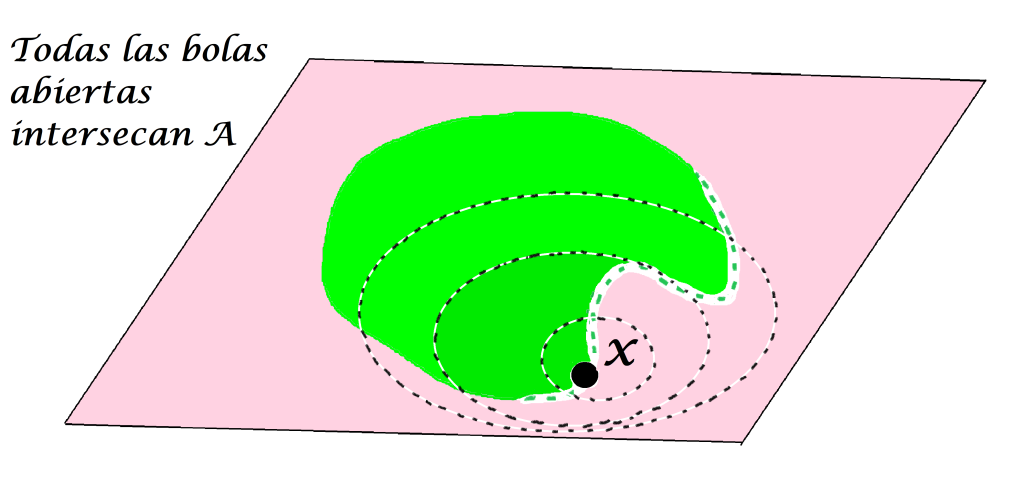
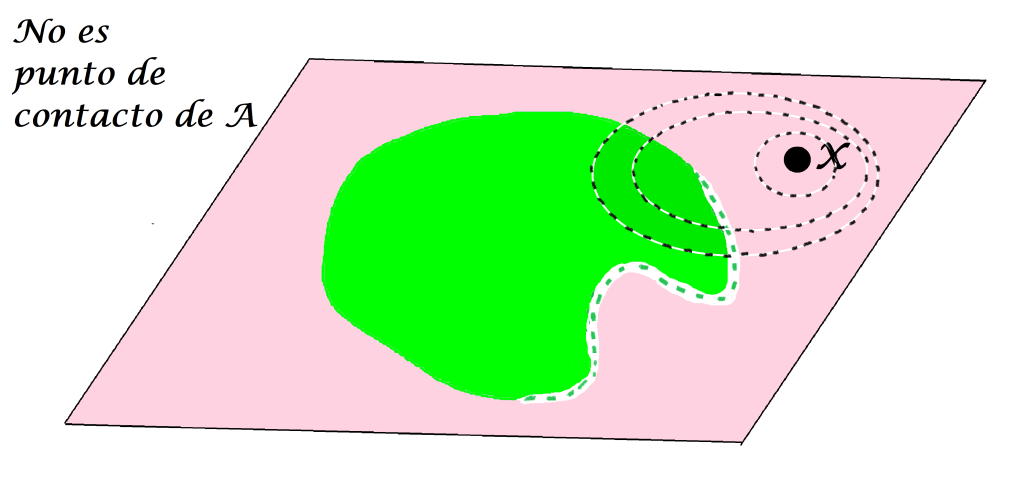
Pero si existe una bola abierta con centro en $x$ que no interseca al conjunto $A,$ $x$ no será punto de contacto, incluso si sí tuviera alguna bola que sí interseca al conjunto $A.$
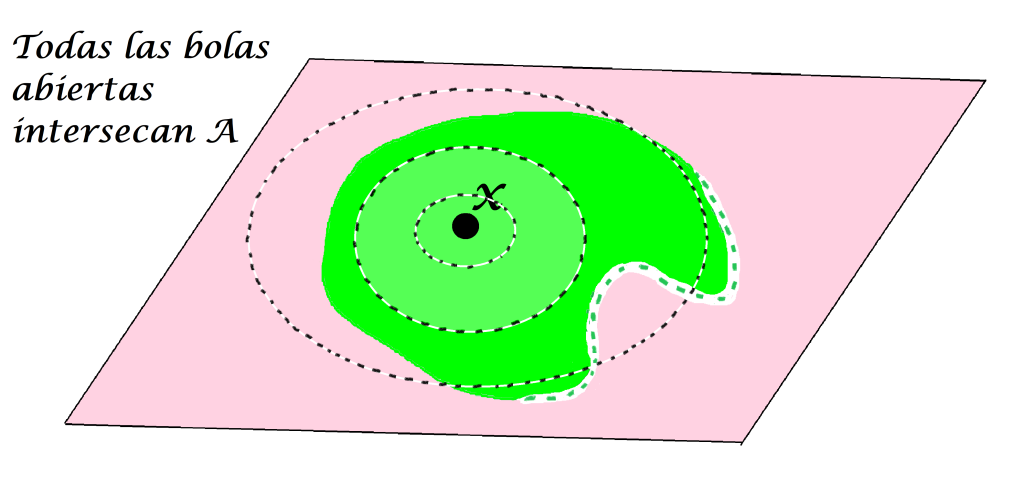
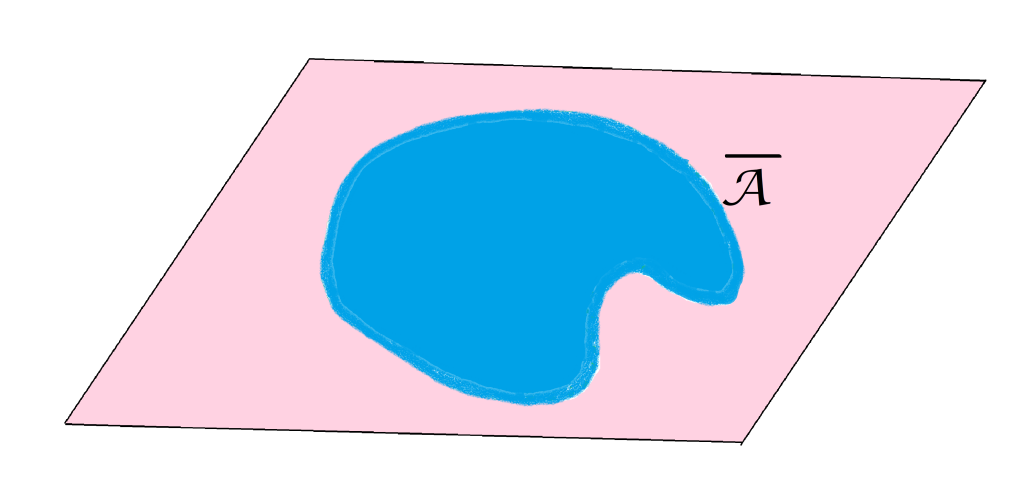
Definición. Cerradura o adherencia de un conjunto. El conjunto formado por todos los puntos de contacto es denominado la cerradura de $A$ en $(X,d)$, y se denota como:
$$ \overline {A} := \{x \in X| x \text{ es punto de contacto de A}\}$$
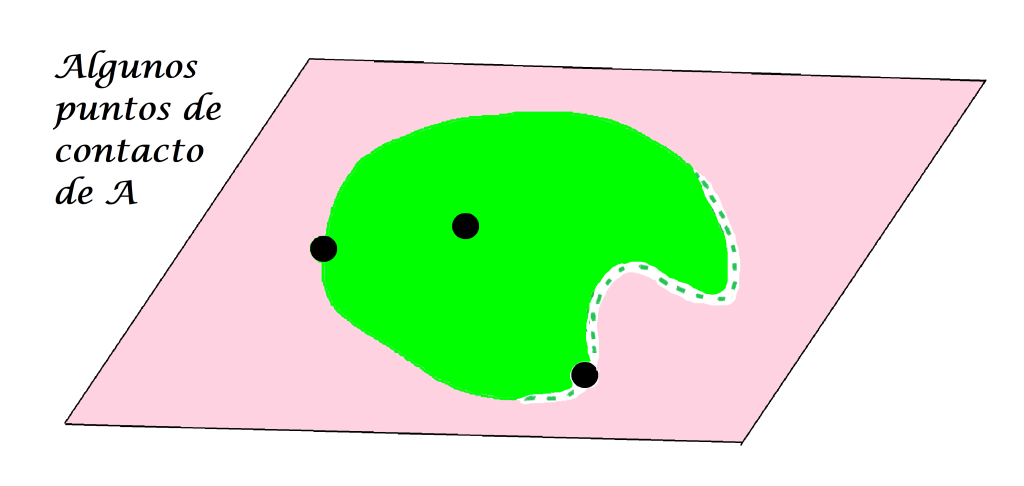
Todos los puntos de contacto de $A$.
Definición. Conjunto cerrado. Diremos que un conjunto $A \subset X$ es un conjunto cerrado en $(X,d)$ si $A=\overline{A}$.
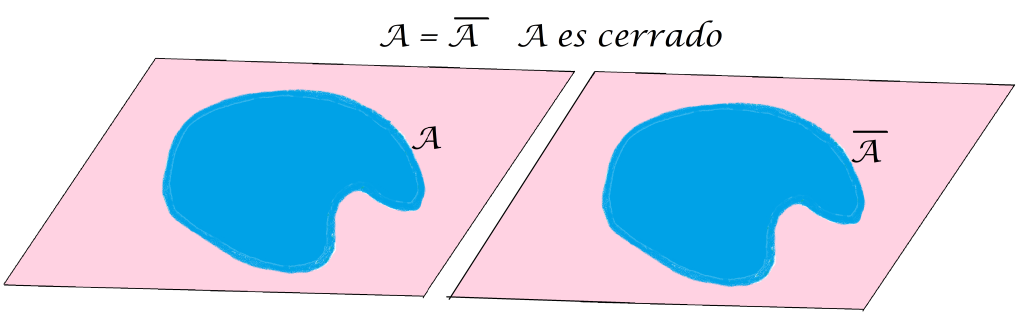
Si pruebas que para todo $A \subset X$ se satisface que $A \subset \overline{A}$ notarás que un conjunto $A$ es cerrado cuando todos sus puntos de contacto están en $A$, es decir, cuando $\overline{A} \subset A$. En el ejemplo que estamos manejando, $A$ no es cerrado, pues tiene puntos de contacto que no están en $A$:
Pero si $A$ fuera considerado inicialmente de esta forma, sí coincide con su cerradura y por tanto, es cerrado:
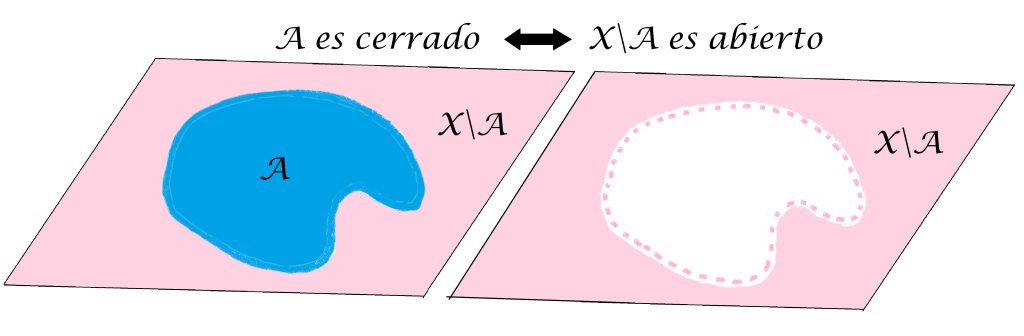
Al final de esta sección se te propondrá como ejercicio demostrar que $A \subset X$ es un conjunto cerrado en $(X,d)$ si y solo sí su complemento $X \setminus A$ es un conjunto abierto en $(X,d)$.
Definición. Bola cerrada. Sea $(X,d)$ un espacio métrico. Considera un punto $x \in X$ y $\varepsilon \in \mathbb {R}, \, \varepsilon>0$. La bola cerrada con centro en $x$ y radio $\varepsilon$ se define como el conjunto de puntos en $X$ tales que el valor de su distancia al punto $x$ es menor o igual que $\varepsilon$. Se denota como:
$$\overline{B}(x,\varepsilon) := \{y \in X | d(x,y) \leq \varepsilon \}$$
Nota: A diferencia de la bola abierta, la bola cerrada sí incluye a los puntos cuya distancia al centro es exactamente $\varepsilon$.
Antes de poner un círculo «cerrado» como representación de una bola cerrada, enunciemos la siguiente:
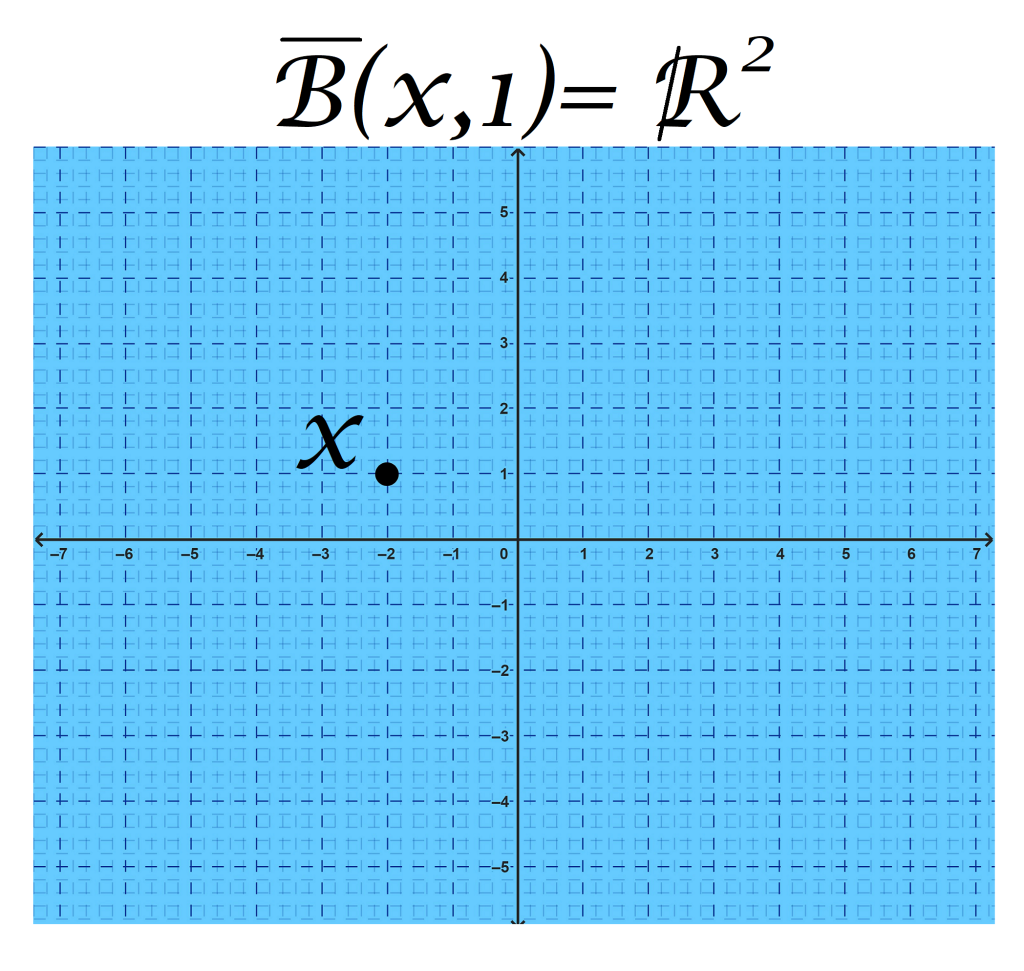
Proposición. La cerradura de una bola abierta $B(x,\varepsilon)$ (denotado como $\overline{B(x,\varepsilon)}$) no coincide, necesariamente con la bola cerrada $\overline{B}(x,\varepsilon)$. Veamos un contraejemplo con la métrica discreta en $\mathbb{R}^2$ y con $\varepsilon=1$.
Dado un punto $x$ en $\mathbb{R}^2$, según la definición, la bola cerrada de radio $1$ con centro en $x$ es el conjunto:
\begin{align*}
\overline{B}(x,1) :&= \{y \in \mathbb{R}^2 | d(x,y) \leq 1\}\\
&= \mathbb{R}^2
\end{align*}
Pues la distancia entre dos puntos en la métrica discreta solo puede ser $0$ o $1$.
Pero si consideramos que para todos los puntos $y$ de $\mathbb{R}^2$ la bola abierta $B(y,1)= \{y\}$, (pues la distancia entre $y$ y el resto de los puntos en $\mathbb{R}^2$ no es menor que $1$), veremos que todos los puntos en $\mathbb{R}^2$ que son distintos de $x$ tienen una bola abierta que no interseca a $B(x,1)$, por lo tanto no hay ningún punto de $\mathbb{R}^2$ diferente de $x$ que esté en la cerradura de $B(x,1)= \{x\}$. En conclusión $\overline{B(x,1)}=\{x\}$.
Proposición. En espacios normados la cerradura de una bola abierta sí es la bola cerrada. Es decir $\overline{B(x,\varepsilon)} = \overline{B}(x,\varepsilon)$. La demostración se propone como ejercicio.
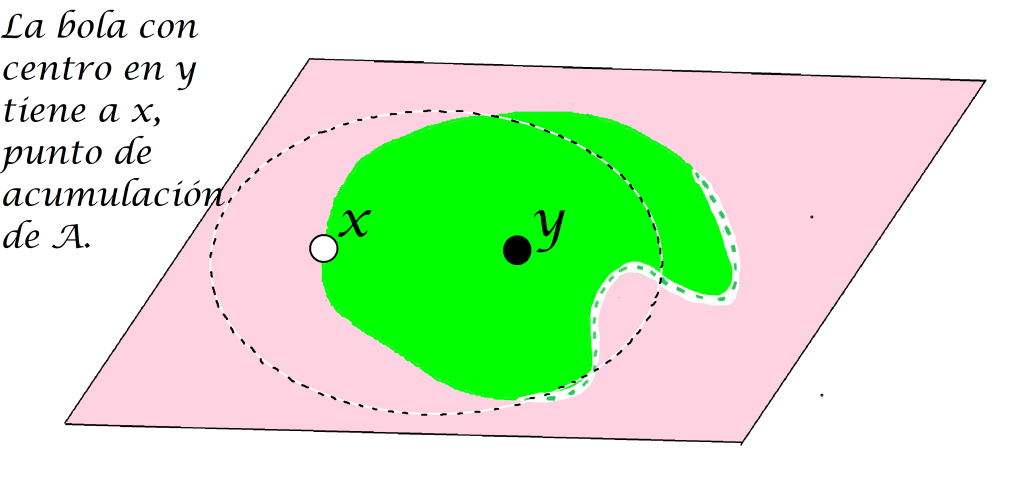
Definición. Punto de acumulación. Sea $A$ un subconjunto de un espacio métrico $(X,d)$ y sea $x \in X$. Decimos que $x$ es punto de acumulación de $A$ en $(X,d)$ si para todo $ \varepsilon >0$ se cumple que $(B(x,\varepsilon) \setminus \{ x \}) \cap A \neq \emptyset$. Nota que a diferencia del punto de contacto, el punto de acumulación se descarta de la intersección entre las bolas abiertas y $A$.
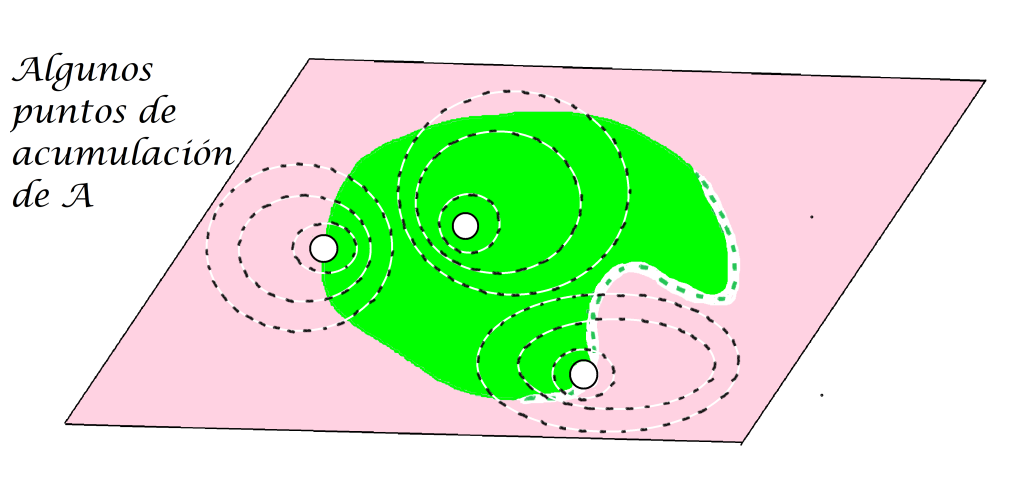
¿Es un punto de contacto también un punto de acumulación en cualquier métrica?
Proposición. Toda bola abierta que tiene un punto de acumulación de $A$, tiene también una cantidad infinita de puntos en $A.$
Demostración:
Supón que $x \in X$ es un punto de acumulación de $A$ y que $x \in B(y,\varepsilon), y \in X, \varepsilon>0$.
Supón también que, contrario a lo que se quiere demostrar, esta bola abierta tiene una cantidad finita de puntos en $A$, digamos $\{x_1,x_2,…,x_n\}$ distintos de $x$.
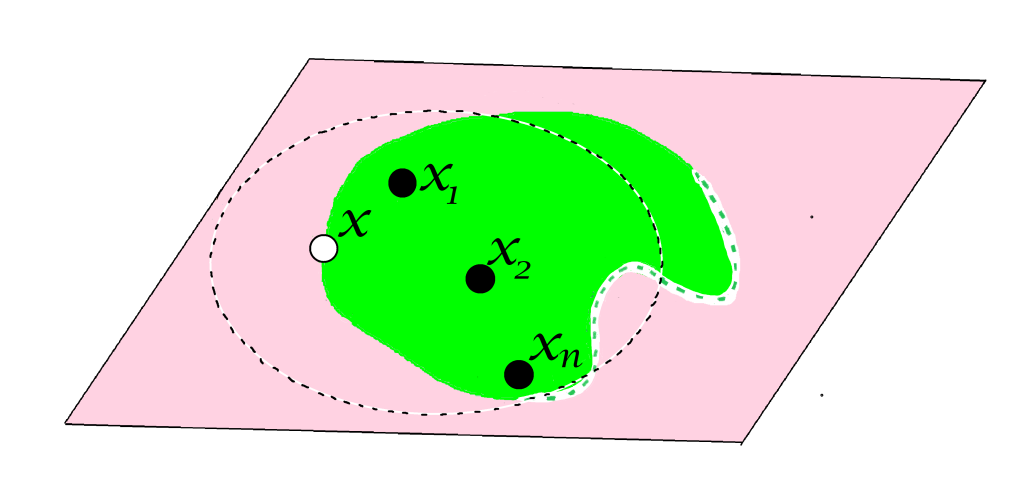
Considera $\varepsilon_{i}:=d(x,x_i), \, i=1,2,…,n \,$ la distancia entre cada uno de ellos a $x$. Sea $\varepsilon_0>0$ tal que $B(x,\varepsilon_0) \subset B(y,\varepsilon).$ Esta $\varepsilon_0$ existe porque $x$ es elemento de $B(y,\varepsilon) \, $ y toda bola abierta es un conjunto abierto en el espacio métrico (se dejará como ejercicio al final de esta sección).
Sea $\varepsilon_{m}= min\{\varepsilon_{i}|i=0,…,n\}$. Entonces el conjunto $B(x,\varepsilon_{m})\setminus \{x\}$ deja fuera todos los puntos de $A$, pues para todo $ \, x_i, i=1,…,n$ pertenecientes a $A \cap B(y,\varepsilon), \varepsilon_{m} \leq d(x,x_i)$, por lo tanto existe una bola abierta que, al quitarle el punto $x$ no interseca a $A$.
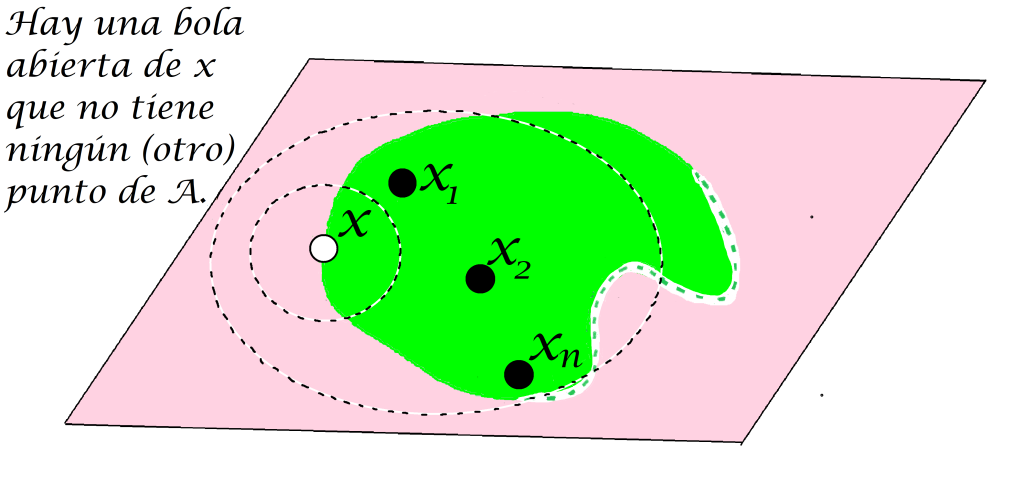
Entonces $x$ no es un punto de acumulación de $A$, lo cual es una contradición a la hipótesis. Por lo tanto una bola abierta que tenga un punto de acumulación de $A$, tiene también una cantidad infinita de puntos en $A$.
Nota: Se puede concluir también que un conjunto finito no tiene puntos de acumulación.
Definición. Punto frontera de un conjunto. Sea $A$ un subconjunto del espacio métrico $(X,d)$ y sea $x \in X$. Decimos que $x$ es punto frontera de $A$ en $(X,d)$ si para toda $\varepsilon > 0$ se cumple que $B(x,\varepsilon) \cap A \neq \emptyset$ y también $B(x,\varepsilon) \cap (X/A) \neq \emptyset$ .
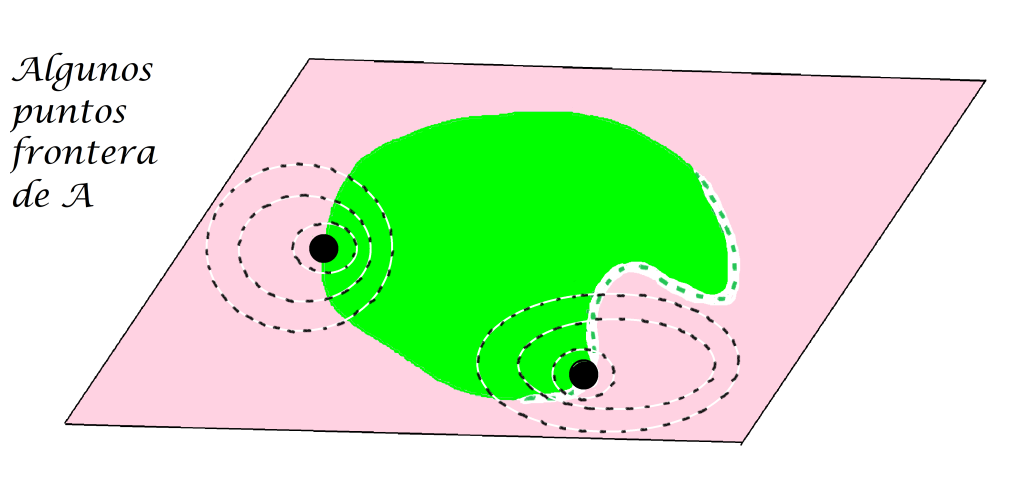
Definición. Conjunto frontera de un conjunto. El conjunto formado por todos los puntos frontera es denominado la frontera de $A$ en $(X,d)$, y se denota como:
$$\partial A := \{x \in X| x \text{ es punto frontera de A}\}$$
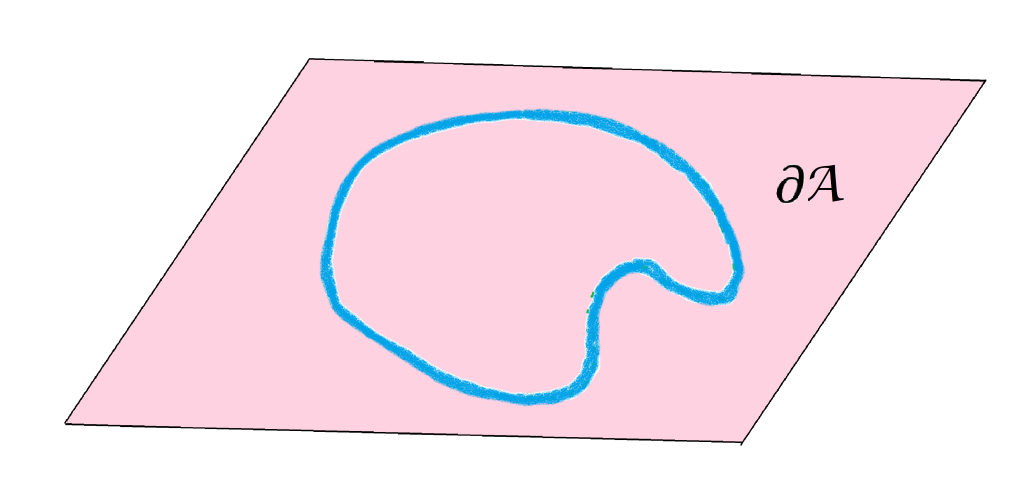
Proposición. Prueba que $\partial A := \overline{A} \setminus Int(A)$. La demostración se propone como ejercicio.
La Topología es un área de las Matemáticas que generaliza estos conceptos del espacio métrico. Estudia familias de subconjuntos de un conjunto $X$ donde los elementos, (que son subconjuntos de $X),$ se denominan abiertos en $X.$ Si esta familia $\tau \subset \mathcal{P}(X) \,$ de abiertos satisface que tiene al conjunto $X$ y al conjunto $\emptyset$ como elementos, que la unión arbitraria de abiertos es también un abierto y que la intersección de dos conjuntos abiertos es un conjunto abierto, decimos que $\tau$ es una topología, o un espacio topológico en $X.$ (Para saber más ver Antonyan, S., Curso de Topología. Facultad de Ciencias, UNAM). Para finalizar con esta sección, veamos por qué un espacio métrico es un espacio topológico:
Proposición. Sea $(X,d)$ un espacio métrico. Entonces cumple con los siguientes axiomas:
- 1. Los conjuntos $X$ y $\emptyset$ son abiertos en $(X,d)$.
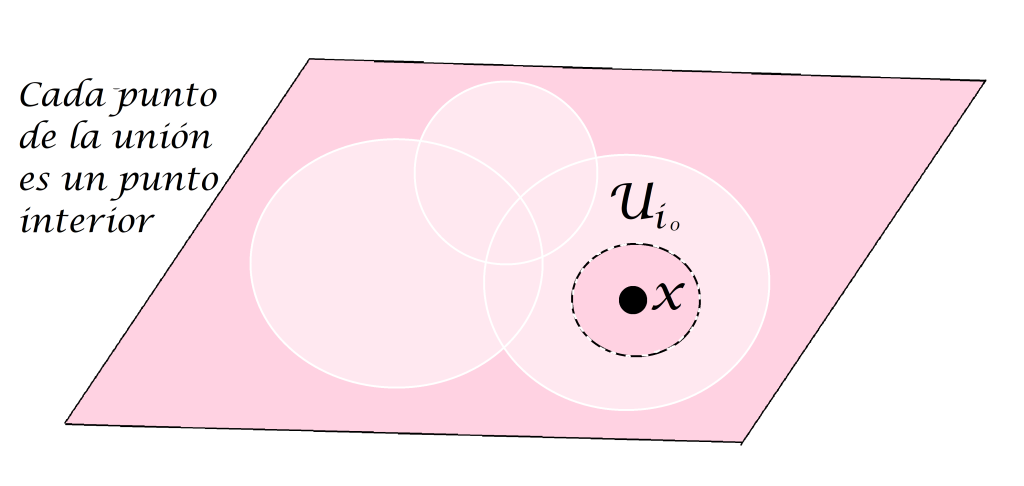
- 2. Si $\{U_i\}:i \in \mathcal{I}$ es una colección de conjuntos abiertos de $X$ entonces la unión $\cup_{i\in \mathcal{I}} \, U_i$ es un conjunto abierto.
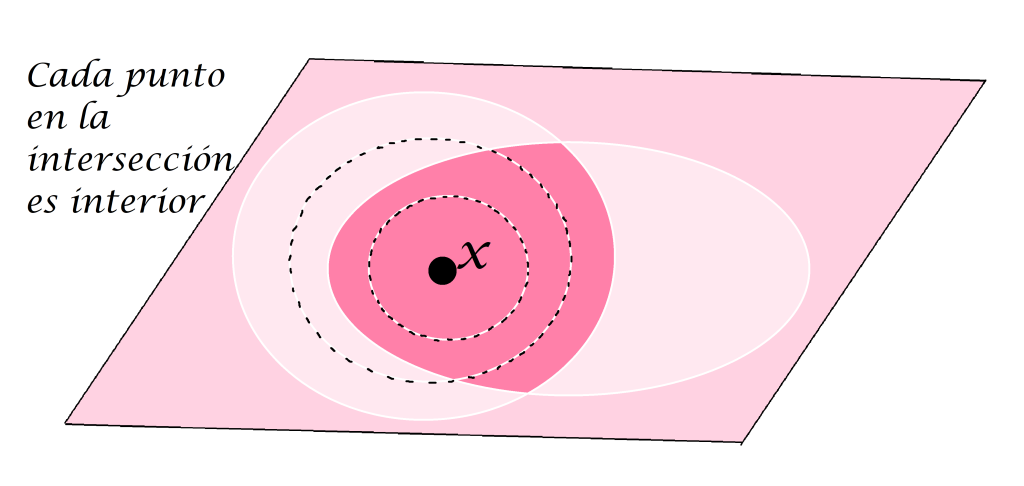
- 3. Si $U$ y $V$ son subconjuntos abiertos de $X$ entonces la intersección $U \cap V$ es un conjunto abierto en $X$.
Demostración:
Para demostrar que $X$ es abierto, demostraremos que cada punto en $X$ es un punto interior de $X$. Sea $x \in X$ y $\varepsilon>0$, por definición $B(x,\varepsilon)= \{y \in X|d(x,y)<\varepsilon \} \subset X. \,$ Por lo tanto para todo $\, x\in X, \, x \in Int(X)$. Se concluye que $X$ es abierto. La propiedad para el conjunto $\emptyset$ se cumple por vacuidad.
Sea $x \in \cup_{i\in \mathcal{I}} \, U_i \,$ entonces $x \in U_{i_0}$ para algún $i_0 \in \mathcal{I}$. Como particularmente $U_{i_0}$ es un conjunto abierto, entonces existe $\varepsilon>0$ tal que$ B(x,\varepsilon) \subset U_{i_0} \subset \cup_{i\in \mathcal{I}} \, U_i$. Por lo tanto para todo $ \, x\in \cup_{i\in \mathcal{I}} \, U_i$ se cumple que $x \in Int(\cup_{i\in \mathcal{I}} \, U_i)$, en consecuencia $\cup_{i\in \mathcal{I}} \, U_i$ es un conjunto abierto en $X$.
Si $x \in U \cap V$ para $U,V$ abiertos en $X$, entonces $x \in U$ y $x \in V$ de modo que existen $\varepsilon_1 >0$ y $\varepsilon_2 >0$ tales que $B(x,\varepsilon_1) \subset U$ y $B(x,\varepsilon_2) \subset V$. Sea $\varepsilon= min \{\varepsilon_1,\varepsilon_2\}$ entonces $B(x,\varepsilon) \subset B(x,\varepsilon_1) \subset U$ y $B(x,\varepsilon) \subset B(x,\varepsilon_2) \subset V$. Así, $B(x,\varepsilon) \subset U \cap V$, probando así que para todo $\, x \in U \cap V, x \in Int(U \cap V)$. Por lo tanto $U \cap V$ es un conjunto abierto en $X.$
Más adelante…
Pondremos en práctica las nociones aquí aprendidas para analizar espacios métricos de funciones. Una vez conocido mejor ese espacio, continuaremos con la generalización de definiciones vistas en los cursos de cálculo y hablaremos de convergencia de sucesiones, límite y continuidad en espacios métricos.
Tarea moral
Sea $X$ un espacio métrico y $A \subset X$. Demuestra que se cumplen las siguientes afirmaciones:
- Una bola abierta en $X$ es un conjunto abierto.
- El conjunto $Int(A)$ es abierto.
- Para todo $A \subset X$, $Int(A) \subset A$.
- Una bola cerrada en $X$ es un conjunto cerrado.
- El conjunto $\overline{A}$ es cerrado.
- $A$ es un conjunto cerrado en $(X,d)$ si y solo sí su complemento $X \setminus A$ es un conjunto abierto.
- La frontera de $A$ es un conjunto cerrado.
- Si $A$ es finito, entonces es cerrado.
- En espacios normados la cerradura de una bola abierta sí es la bola cerrada. Es decir $\overline{B(x,r)} = \overline{B}(x,r)$.
- ¿Es siempre la frontera de una bola abierta $B(x,d)$ el mismo conjunto de puntos $y \in X$ donde se cumple la igualdad $d(x,y)=\varepsilon? \,$ Demuestra que en espacios normados sí ocurre.
- $\partial A = \overline{A} \setminus Int(A)$.
Bibliografía
- Apostol, T., Análisis Matemático (2a ed.). México: Editorial Reverté, 1996. Págs: 60-66 y 74-77.
- Bartle, R.G., The Elements of Real Analysis. New York: J. Wiley, 1964.Págs: 69-74.
- Clapp, M., Análisis Matemático. Ciudad de México: Editorial Papirhos, IM-UNAM, 2013. Págs: 37-43.
- Jost, J., Postmodern Analysis (3rd ed.). New York: Springer-Verlag, 2005. Págs: 84-87.
- Kolmogorov, A.N., Fomin, S.V., Elementos de la Teoría de Funciones y del Análisis Funcional. (2a ed.). Moscú: Editorial MIR, 1975. Págs: 60-62 y 64-66.
- Rudin, W., Principles of Mathematical Analysis (3rd ed.). New York: McGraw–Hill, 1953. Págs: 32-35.

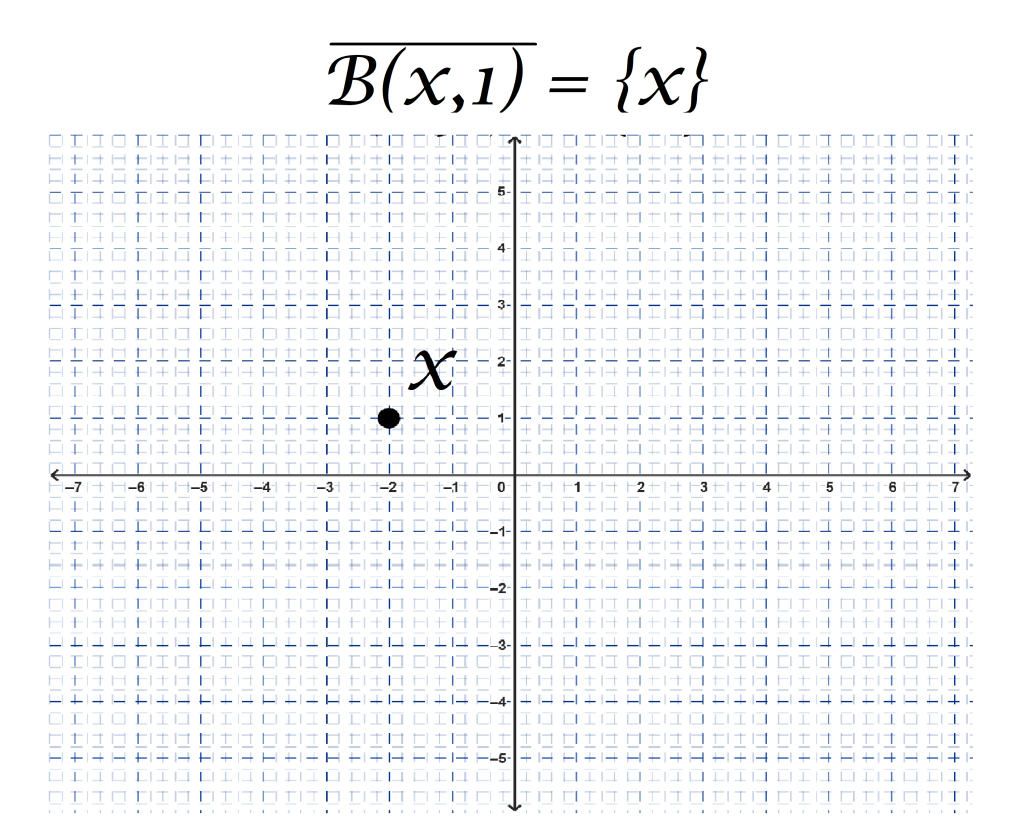
La felicito Lizbeth, muy bonito tu aporte en este block
¡Gracias por sus palabras! Seguiremos trabajando.
Muchas gracias por el contenido, realmente no entendía el tema pero ahora me quedo claro 😀
¡Gracias por tu retroalimentación! Es agradable saber que te ayuden estas notas.