Introducción:
Es momento de interactuar entre dos espacios métricos, $(X,d_X)$ y $(Y,d_Y)$, cada uno con su respectivo conjunto de puntos y métrica definida en ellos. Podemos relacionar puntos del espacio métrico $X$ con puntos en el espacio métrico $Y$. Será natural preguntarse qué ocurre con las distancias en el nuevo espacio métrico, en comparación con el de origen. Considera la siguiente:
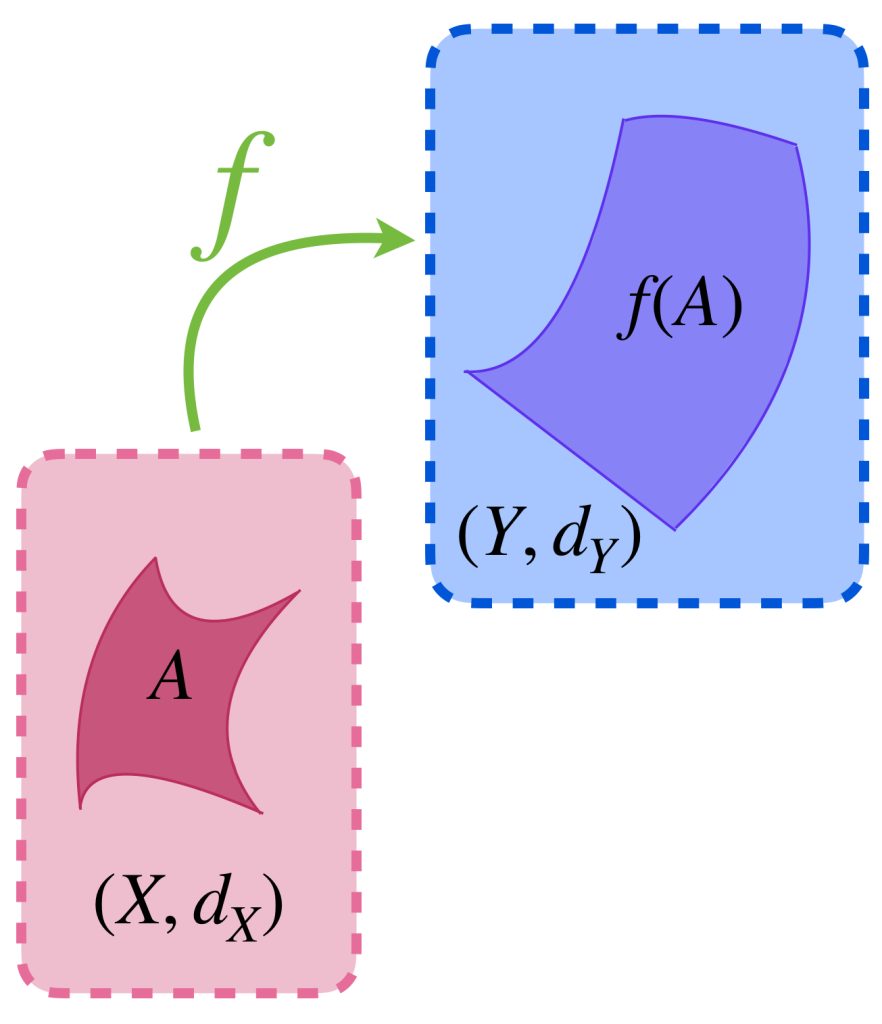
Definición de imagen de un conjunto. Sean $(X,d_X)$ y $(Y,d_Y)$ espacios métricos. Si $A \subset X$ y $f: X \to Y$, es una función, entonces $f \,$ define un conjunto en $Y$ dado por $f(A):=\{f(x)|x\in A\}$, que llamaremos la imagen de $A$ bajo $f \,$ y es la colección de elementos que se le asignan a cada elemento de $A$.
Ahora preguntamos: ¿bajo qué circunstancias una función envía puntos de $A \subset X$ a puntos en $Y$ que se aproximan a algún punto $L \in Y$?
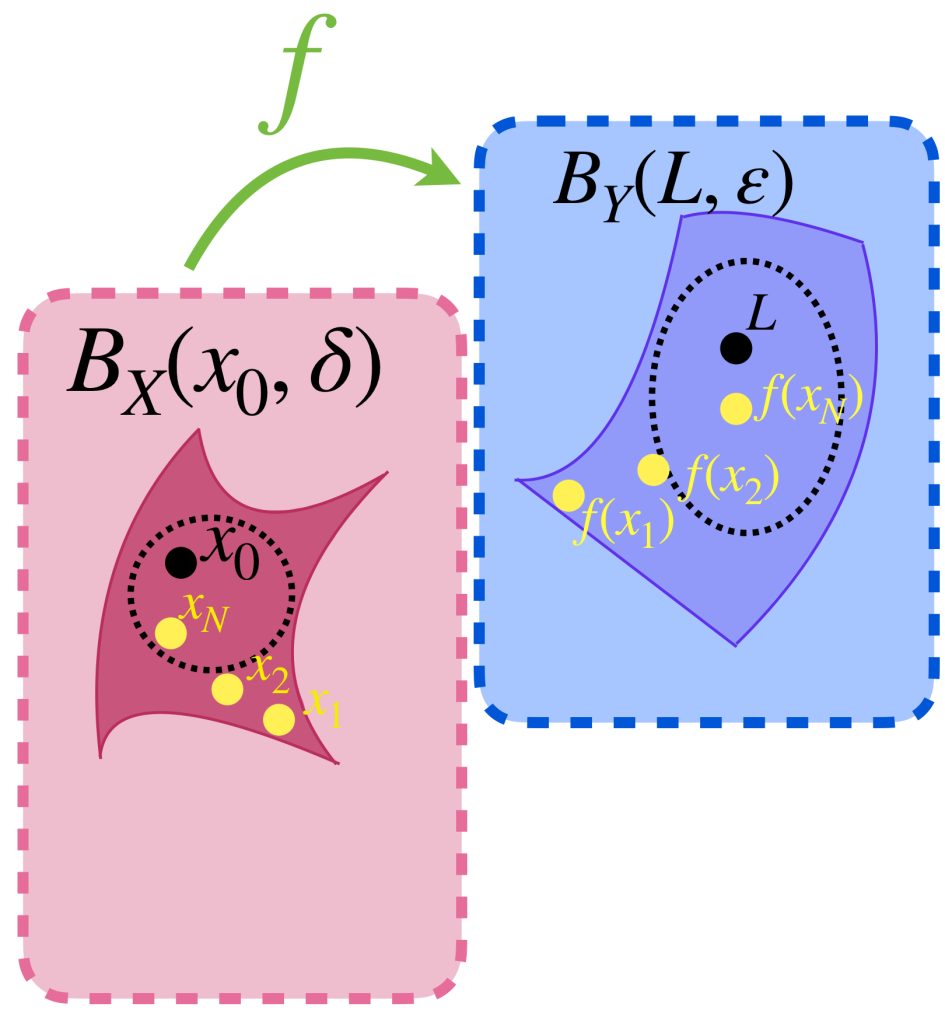
Si $x_0$ es un punto de acumulación en $A$, por definición, todas sus bolas abiertas tienen elementos en $A$ distintos de $x_0$. Podemos así, identificar puntos cercanos a $x_0$, según la distancia $d_X$, que bajo la función $f$ sean enviados a puntos en $Y$ que estén cerca de un punto $L$, según la distancia $d_Y$.
Como los puntos cerca de $L$ en $(Y,d_Y)$ son los que están en la bola de radio $\varepsilon$ con centro en $L,$ se busca conseguir que los puntos cerca de $x_0$ caigan justamente en $B_Y(L,\varepsilon)$. (El subíndice $Y$ en $B_Y$ nos recuerda en qué espacio métrico es considerada la bola abierta. Recuerda que pueden ser diferentes, según la métrica a la que se refiera).
De manera formal tenemos la siguiente:
Definición límite de una función: Sea $f: X \to Y$ una función entre espacios métricos y $x_0$ un punto de acumulación de $A$. Decimos que el límite de $f$, cuando $x$ tiende al punto $x_0$ es $L \in Y$, si ocurre que para todo $\varepsilon >0$ existe $\delta > 0$ tal que para todo $x\neq x_0, \text{ si } d(x,x_0)< \delta$ entonces $d(f(x),L)<\varepsilon$. Se denota como:
$$\underset{x \to x_0}{lim} \,f(x) \,=L$$
Se dice entonces que $f(x) \to L$ cuando $x \to x_0$.
Esta definición se puede expresar en términos de bolas abiertas como sigue: $\, \underset{x \to x_0}{lim} \,f(x) \,=L \,$ si para todo $\varepsilon >0$ existe $\delta > 0$ tal que $f(B_X(x_0,\delta) \setminus \{x_0\}) \subset B_Y(L,\varepsilon)$.
Veamos un resultado que nos permite concluir límites a partir de sucesiones.
Proposición: Considera $A \subset X$ y $x_0 \in A$ un punto de acumulación en $A$. Entonces $$\underset{x \to x_0}{lim} \, f(x) \,=L$$ si y solo si para toda sucesión $(x_n)_{n \in \mathbb{N}}$ en $A \setminus \{x_0\}$ tal que $x_n \to x_0$ ocurre que $$\underset{n \to \infty}{lim} \, f(x_n) \,=L$$.
Demostración:
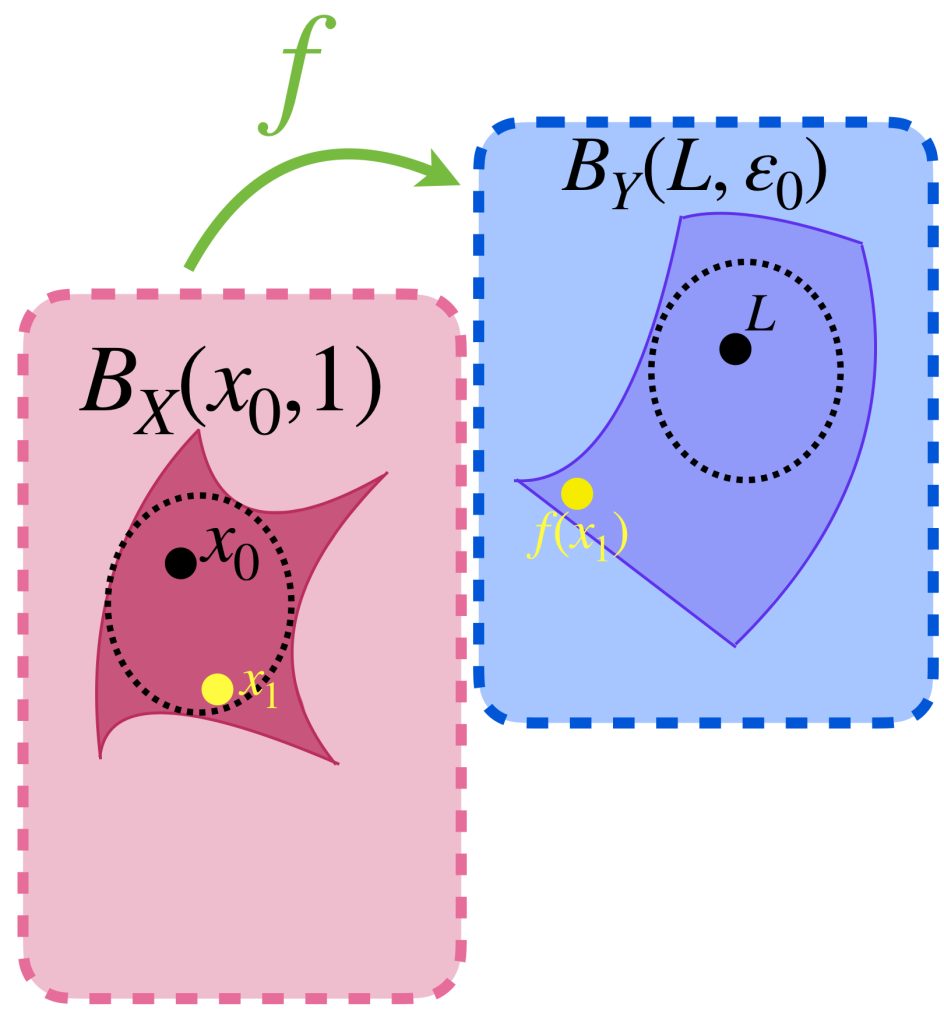
Sea $(x_n)_{n \in \mathbb{N}}$ una sucesión en $A \setminus \{x_0\}$ que converge a $x_0$ y sea $\varepsilon >0$. Como $\underset{x \to x_0}{lim} \, f(x) \,=L$ entonces existe $\delta>0$ tal que para todo $x\neq x_0, \text{ si } d(x,x_0)< \delta \,$ entonces $\, d(f(x),L)<\varepsilon$.
Como $(x_n) \to x_0$, entonces existe $N \in \mathbb{N}$ tal que $\forall \, n\geq N, \, d(x_n,x_0)< \delta$, así $\forall \, n \geq N, \, d(f(x_n),L) < \varepsilon$ por lo tanto $f(x_n) \to L\, $ en $\, Y$.
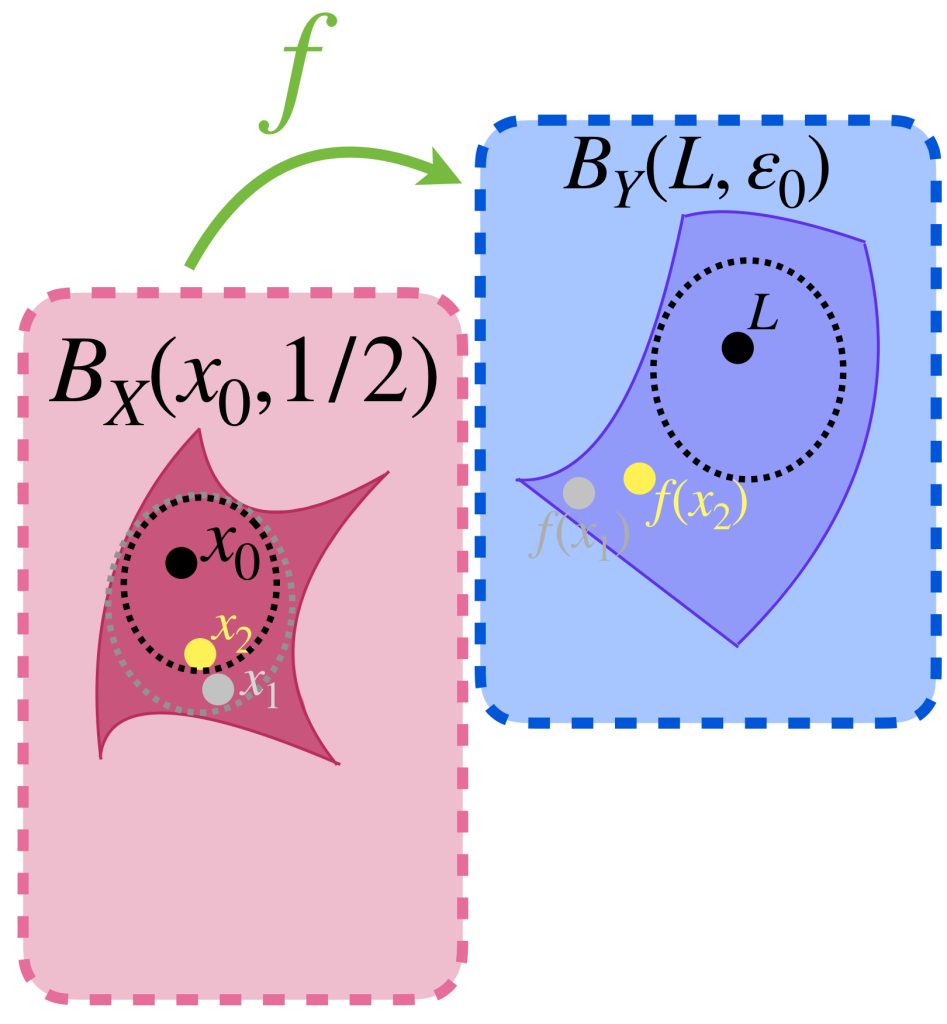
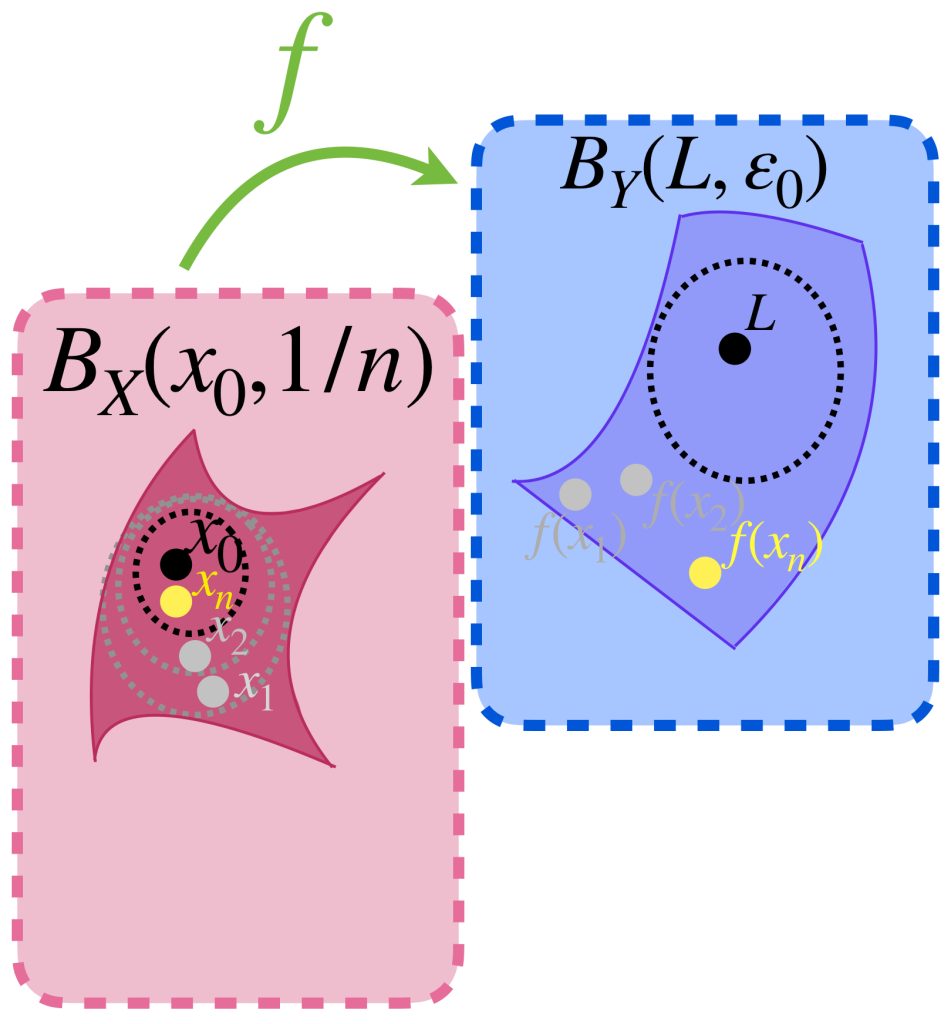
Ahora supón que el recíproco no es cierto. Entonces existe $\varepsilon_0 >0$ tal que $\forall \, \delta>0$ existe $x_0 \neq x_0 \,$ con $\, d_X(x_0,x_0)<\delta$ pero $\, d_Y(f(x_0),L)> \varepsilon$.
De modo que para cada bola abierta con centro en $x_0$ y radio $\frac{1}{n}$ con $n \in \mathbb{N}$ podemos elegir un punto $x_n \in (B_X(x_0,\frac{1}{n}) \setminus \{x_0\})$ pero $\, d_Y(f(x_n),L)> \varepsilon_0$.
La sucesión $x_n \to x_0$ pero la sucesión $(f(x_n))_{n \in \mathbb{N}} \,$ al quedarse siempre fuera de la bola abierta $B_Y(L,\varepsilon_0)$ no converge a $L$, lo cual es una contradicción.
Por lo tanto $\, \underset{x \to x_0}{lim} \, f(x) \,=L$.
Las siguientes proposiciones son propiedades de límites de funciones en los espacios métricos mencionados:
Proposición: Sean $f:A \to \mathbb{C}$ y $g:A \to \mathbb{C}$. Si $x_0$ es un punto de acumulación en $A$ y $\underset{x \to x_0}{lim}\, f(x) \,=L_1 \,$ y $\, \underset{x \to x_0}{lim}\, g(x) \,=L_2$, se tiene que:
a) $\underset{x \to x_0}{lim} \, f(x) \pm g(x) \,=L_1 \pm L_2$
b) $\underset{x \to x_0}{lim} \, f(x)g(x) \,=L_1 L_2$
c) $\underset{x \to x_0}{lim} \, f(x) / g(x) \,=L_1 / L_2$ cuando $L_2 \neq 0$
La demostración se deja como ejercicio.
Proposición: Sean $f,g: A \subset X \to \mathbb{R}^n\, $ Si se definen
$(f+g)(x)=f(x)+g(x)$ y $(f \cdot g)(x)=f(x) \cdot g(x)$ entonces si $x_0$ es un punto de acumulación en $A$ y $\underset{x \to x_0}{lim}\, f(x) \,=L_1 \,$ y $\, \underset{x \to x_0}{lim} \,g(x) \,=L_2$, se tiene que:
a) $\underset{x \to x_0}{lim} \, f(x) \pm g(x) \,=L_1 \pm L_2$.
b) $\underset{x \to x_0}{lim} \, f(x) \cdot g(x) \,=L_1 \cdot L_2$.
c) $\underset{x \to x_0}{lim} \, \lambda f(x) \,= \lambda L_1 \,$con $\,\lambda \in \mathbb{R}$.
La demostración se deja como ejercicio.
Más adelante…
Veremos el caso para cuando la función sí está definida en $x_0 \in A \subset X$ y más aún, la función tiene como límite al punto $f(x_0)$. Hablaremos así de funciones continuas en un punto $x_0$ y observaremos el efecto que estas funciones producen en subconjuntos abiertos y cerrados de un espacio métrico.
Tarea moral
- Demuestra las dos proposiciones anteriores.
Enlaces
- Análisis Matemático.
- Enlace a entrada anterior.
- Enlace a entrada siguiente.