Introducción
Ya se ha visto que en una hilera armónica se tienen cuatro puntos colineales $A,B,C,D$, donde el segmento $AB$ está dividido por $C$ y $D$ en razones cuya razón es:
$\hspace{15em} \frac{AC}{CB} / \frac{AD}{DB} = -1.$
En este caso $A$ y $B$ están separados armónicamente por $C$ y $D$, pero que pasaría si estos cuatro puntos estuvieran en posiciones cualesquiera en la recta que se encuentran, es aquí donde entra la definición de razón cruzada.
Razón cruzada para hilera y haces
Definición. (Razón Cruzada) Dados cuatro puntos colineales distintos $A,B,C,D$ en una recta, diremos que la razón cruzada es:
$\frac{AC}{CB} / \frac{AD}{DB} = \{ ABCD \} = k$ con $k \neq -1.$
Lo denotaremos $\{ ABCD \} $.
También se le conoce como razón anarmónica y razón doble.
Observación. Si los cuatro puntos son armónicos, entonces $\{ ABCD \} = -1 $, de igual forma inversamente.
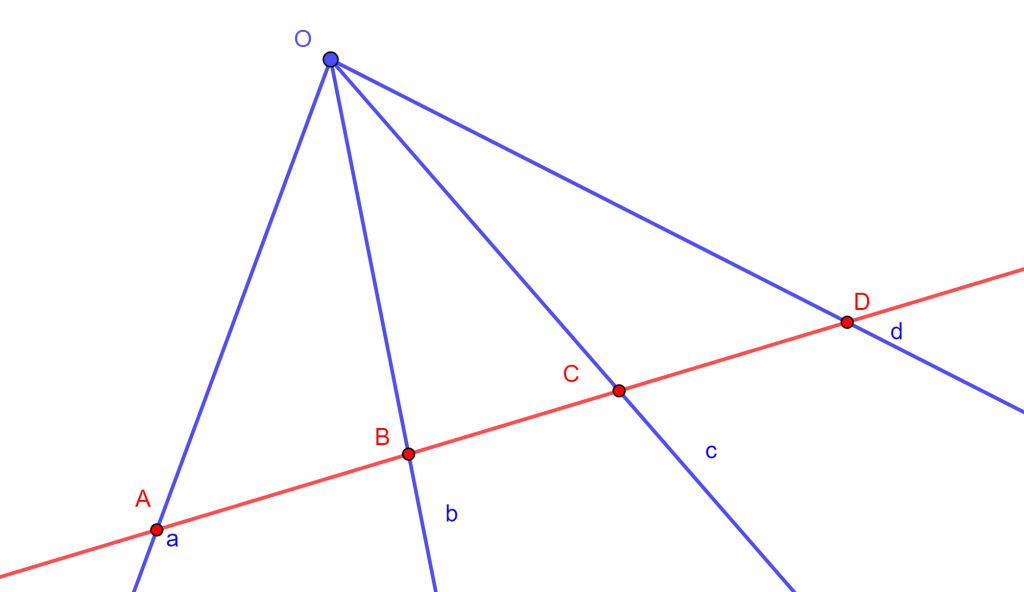
Definición. (Razón Cruzada con líneas concurrentes) Sean cuatro rectas concurrentes $OA$, $OB$, $OC$ y $OD$ en un punto $O$, que no se forme un haz armónico, entonces la razón cruzada es:
$\frac{sen (AOC)}{sen (COB)} / \frac{sen (AOD)}{sen (DOB)} $,
se denotará como $O \{ ABCD \} $. De igual forma, la razón cruzada de cuatro líneas concurrentes $a,b,c,d$ se denotará $\{ a,b,c,d \} $.
Observación. Dados cuatro puntos colineales $A,B,C, D$ se tienen estos casos:
1) $\{ ABCC \} =1$ esto, ya que $\{ ABCC \} =\frac{AC}{CB} / \frac{AC}{CB} = \frac{AC * CB}{CB * AC} =1$.
2) $\{ ABCB \} =0$ esto ya que $\{ ABCB \} =\frac{AC}{CB} / \frac{AB}{BB} = \frac{AC * BB}{CB * AB} =0$.
3) $\{ ABCA \} =\infty $ esto ya que $\{ ABCA \} =\frac{AC}{CB} / \frac{AA}{AB} = \frac{AC * AB}{CB * AA} =\infty $.
Por lo cual se puede demostrar que si la razón cruzada de cuatro puntos tiene uno de los valores $1,0, \infty $ entonces dos de los puntos coinciden.
Teorema. (Razón Cruzada) Si se tienen cuatro puntos distintos $A,B,C,D$ en una recta y $O$ un punto (no está en la recta) entonces:
$\{ ABCD \} =O \{ ABCD \} .$
Demostración. Para demostrar el teorema se usará lo siguiente, si dos puntos finitos $A$ y $B$ distintos en una recta, sea $P$ otro punto de la misma recta y $C$ un punto que no está en la recta, entonces
$\frac{AP}{PB}=\frac{CA*sen (ACP)}{CB*sen (PCB)}$
Entonces usando lo anterior:
$\frac{AC}{CB}=\frac{OA*sen (AOC)}{OB*sen (COB)}$ y $\frac{AD}{DB}=\frac{OA*sen( AOD)}{OB*sen (DOB)}$
$\{ ABCD \} = \frac{AC}{CB} / \frac{AD}{DB}=\frac{OA*sen(AOC)}{OB*sen(COB)} / \frac{OA*sen(AOD)}{OB*sen(DOB)}=\frac{sen(AOC)}{sen(COB)} / \frac{sen(AOD)}{sen( DOB)}=O \{ ABCD \}.$
$\square$
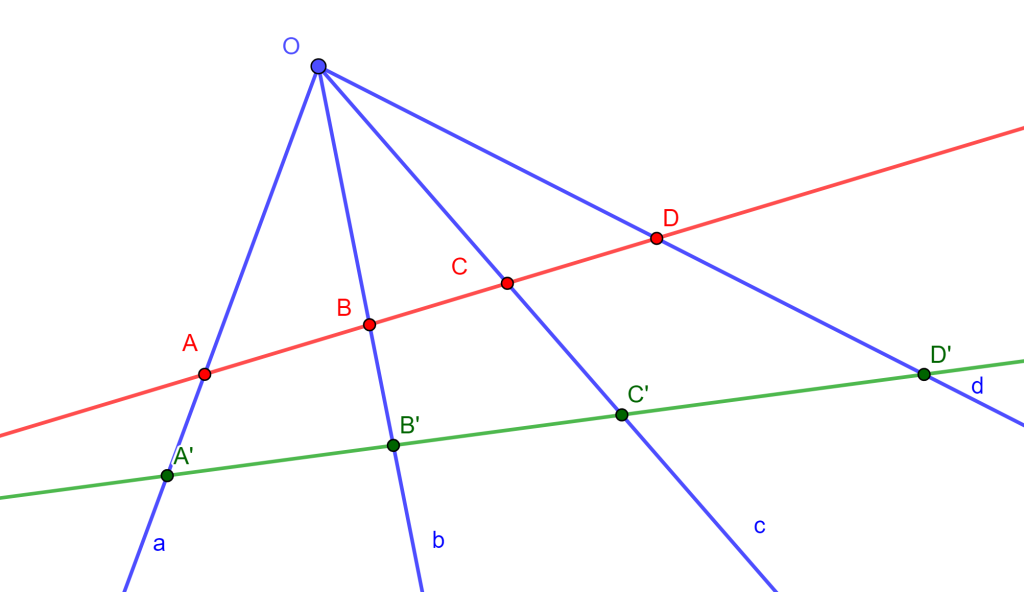
Corolario. Sean dos rectas transversales a cuatro líneas de un haz, de las cuales ninguna pasa por el vértice, cortan a estas líneas en $A,B,C,D$ y $A’,B’,C’,D’$ respectivamente, entonces $\{ ABCD \} = \{ A’B’C’D’ \} $.
Demostración. $\{ ABCD \} = O\{ ABCD \} = O\{ A’B’C’D’ \} =\{ A’B’C’D’ \}.$
$\square$
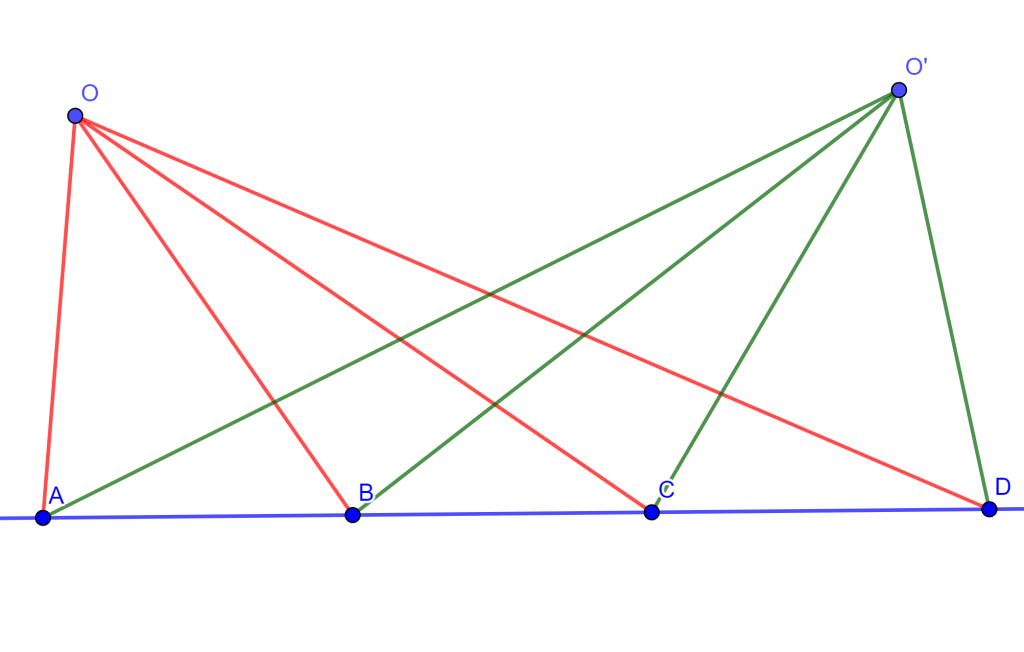
Corolario. Sean dos haces con vertices en $O$ y $O’$ son subtendidos por la misma hilera de puntos $A,B,C,D$ entonces $O\{ ABCD \} = O’\{ ABCD \}$.
Demostración. $O\{ ABCD \} = \{ ABCD \}=O’\{ ABCD \}.$
$\square$
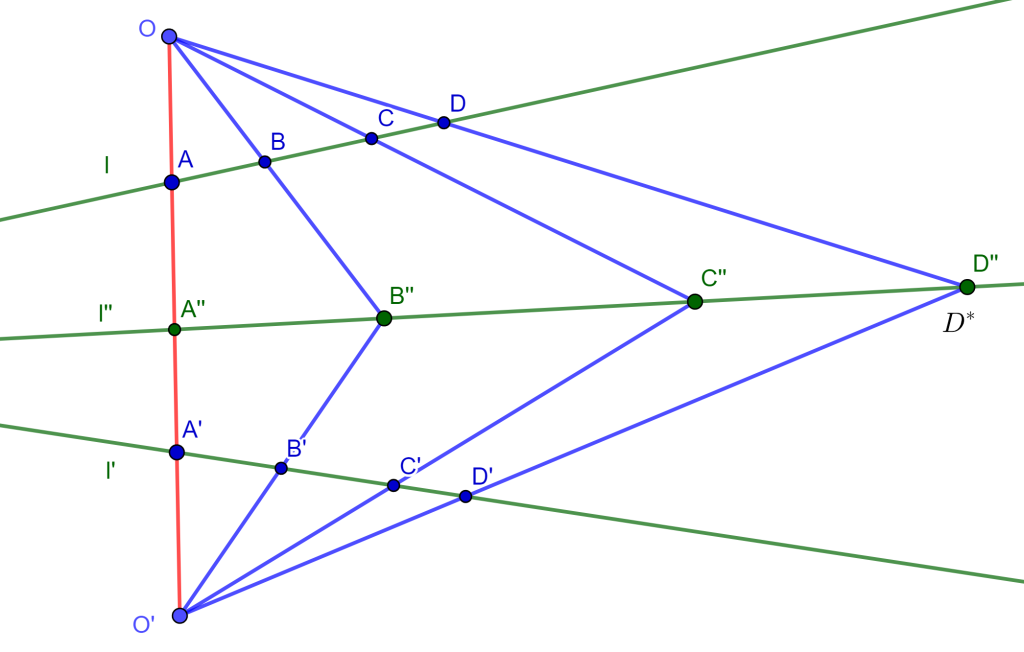
Corolario. Sean $l$ y $l’$ dos rectas en posición cualquiera y sean $A,B,C,D \in l$ y $A’,B’,C’,D’ \in l’$. Si $\{ ABCD \} = \{ A’B’C’D’ \} $ y $O$ y $O’$ son colineales con $A$ y $A’$, entonces las intersecciones $OB$ y $O’B’$, $OC$ y $O’C’$, $OD$ y $O’D’$ son colineales.
Demostración. Sea $l’$$’$ la recta que contiene a $B’$$’$ y $C’$$’$, y sean $A’$$’=l’$$’ \cap OO’$, $D’$$’=OD \cap O’D’$ y sea $D^*=l’$$’ \cap O’D’$.
Tenemos que $\{ ABCD \} = \{ A’B’C’D’ \} $ entonces $\{ A’B’C’D’ \} = \{ A’$$’B’$$’C’$$’D^* \} $.
$\Rightarrow $ $\{ ABCD \} = \{ A’$$’B’$$’C’$$’D^* \} $
$\Rightarrow $ $O\{ ABCD \} = \{ A’$$’B’$$’C’$$’D^* \} $
$\Rightarrow $ $D’$$’=D^*.$
$\square$
Más adelante…
Se seguirá abordando unas propiedades de la razón cruzada y además se construirá un cuarto elemento dada una razón.
Entradas relacionadas
- Ir a Geometría Moderna II
- Entrada anterior del curso: Ejercicios Unidad 3
- Siguiente entrada del curso: Construcción del cuarto elemento dada la razón