$ \textit{ MATERIAL EN REVISIÓN}$
Introducción
Probablemente estés familiarizado con las funciones continuas de los cursos de cálculo. Esta noción se retoma para funciones entre espacios métricos. Diremos que una función entre espacios métricos $X$ y $Y,$ $f:X \to Y$ es continua en un punto $x_0$ de $X$ si para puntos que están «junto a» $x_0$ en $X$, los puntos correspondientes bajo la función $f$ también están junto a $f(x_0).$ Este tipo de funciones nos permite identificar propiedades entre los espacios métricos que relaciona. En esta entrada comenzaremos a explorar algunos resultados. Comencemos con la definición:
Definición. Función continua. Sean $(X,d_X)$ y $(Y,d_Y)$ dos espacios métricos. Diremos que una función $\phi: X \to Y$ es continua en el punto $x_0 \in X$ si para todo $\varepsilon >0$ existe $\delta > 0$ tal que para todo $x \in X$ si $d_X(x,x_0) < \delta$ entonces $d_Y(\phi(x), \phi(x_0))<\varepsilon$. Si $\phi:X \to Y$ es continua en cada punto de $A \subset X$, diremos que $\phi$ es continua en $A$.
Si comparas esta definición con la de la entrada anterior, Límite de una función, estarás de acuerdo en que una funcíon $\phi: X \to Y$ es continua en $x_0 \in X$ si
$$\underset{x \to x_0}{lim} \,\phi (x) \,=\phi(x_0)$$
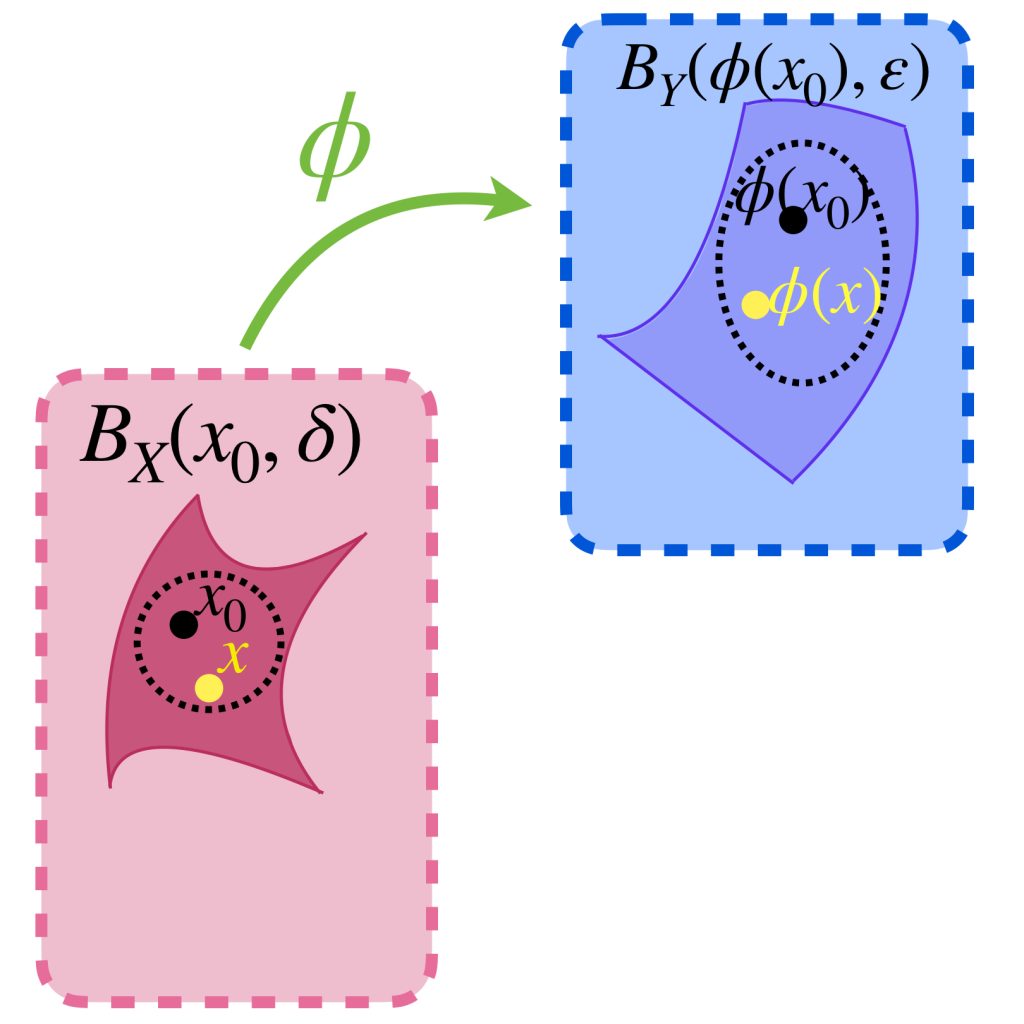
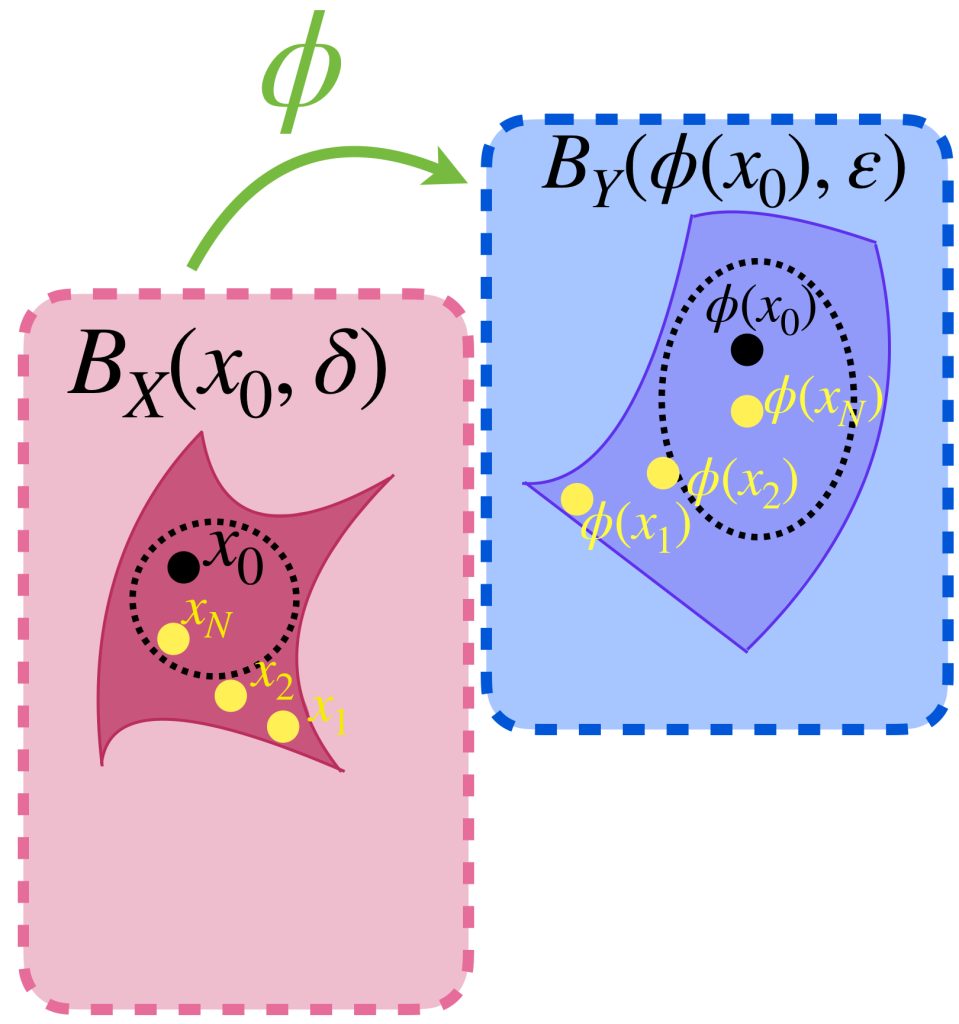
Esta definición se puede expresar en términos de bolas abiertas como sigue: La función $\phi: X \to Y$ es continua en $x_0 \in X$ si para todo $\varepsilon >0$ existe $\delta > 0$ tal que $\phi(B_X(x_0,\delta)) \subset B_Y(\phi(x_0),\varepsilon)$. Observa que en la definición de continuidad, a diferencia de la de límite, no se excluye al punto de continuidad $x_0$.
Ejemplos
La función constante
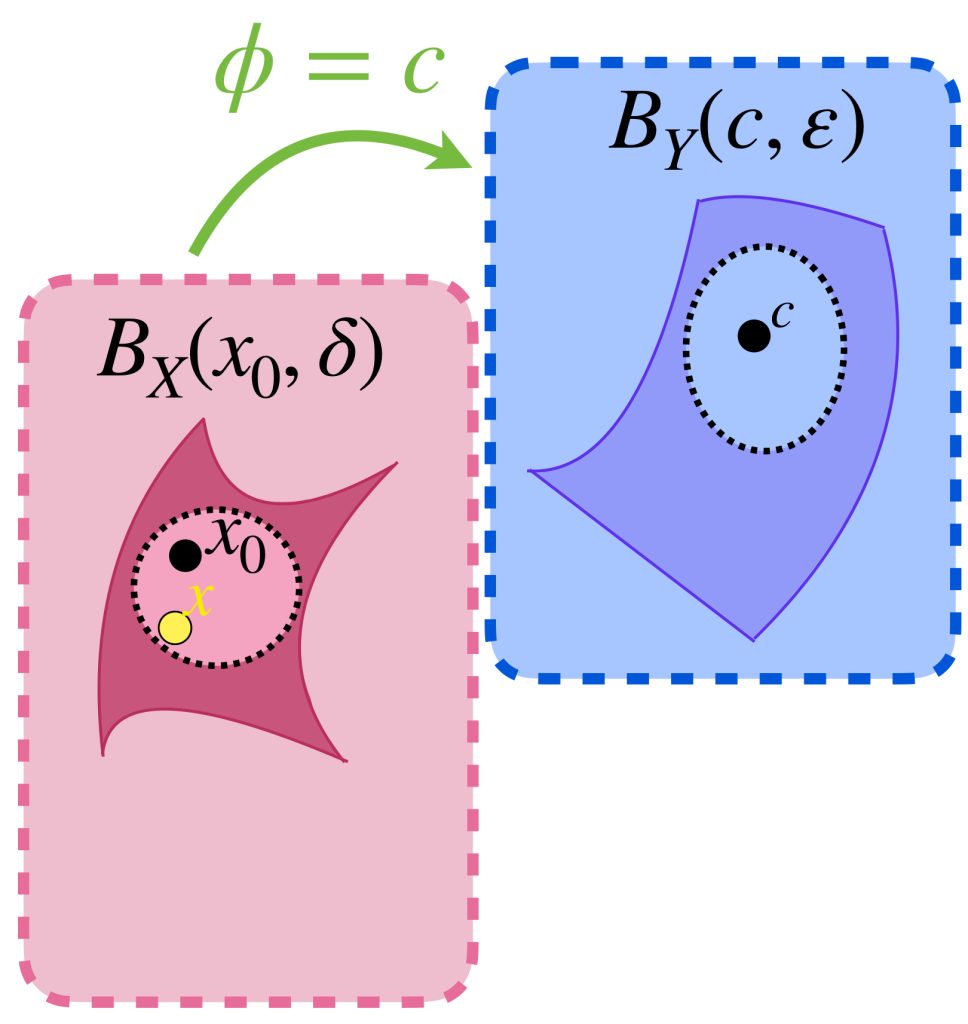
Para cualesquiera dos espacios métricos $(X,d_X)$ y $(Y,d_Y)$ la función constante $\phi :X \to Y$ tal que para todo $x \in X, \, \phi (x) = c$ para algún $c \in Y$, es continua en cualquier punto de $X.$
Demostración:
Sea $\varepsilon >0$ y $\delta =1$ (cualquier valor para delta funciona). Sea $x_0 \in X$. Entonces si $d_X(x_0,x)<1$ se cumple que $d_Y (\phi(x_0),\phi(x))=d_Y (c,c)=0< \varepsilon.$ Por lo tanto, $f$ es continua en $X.$
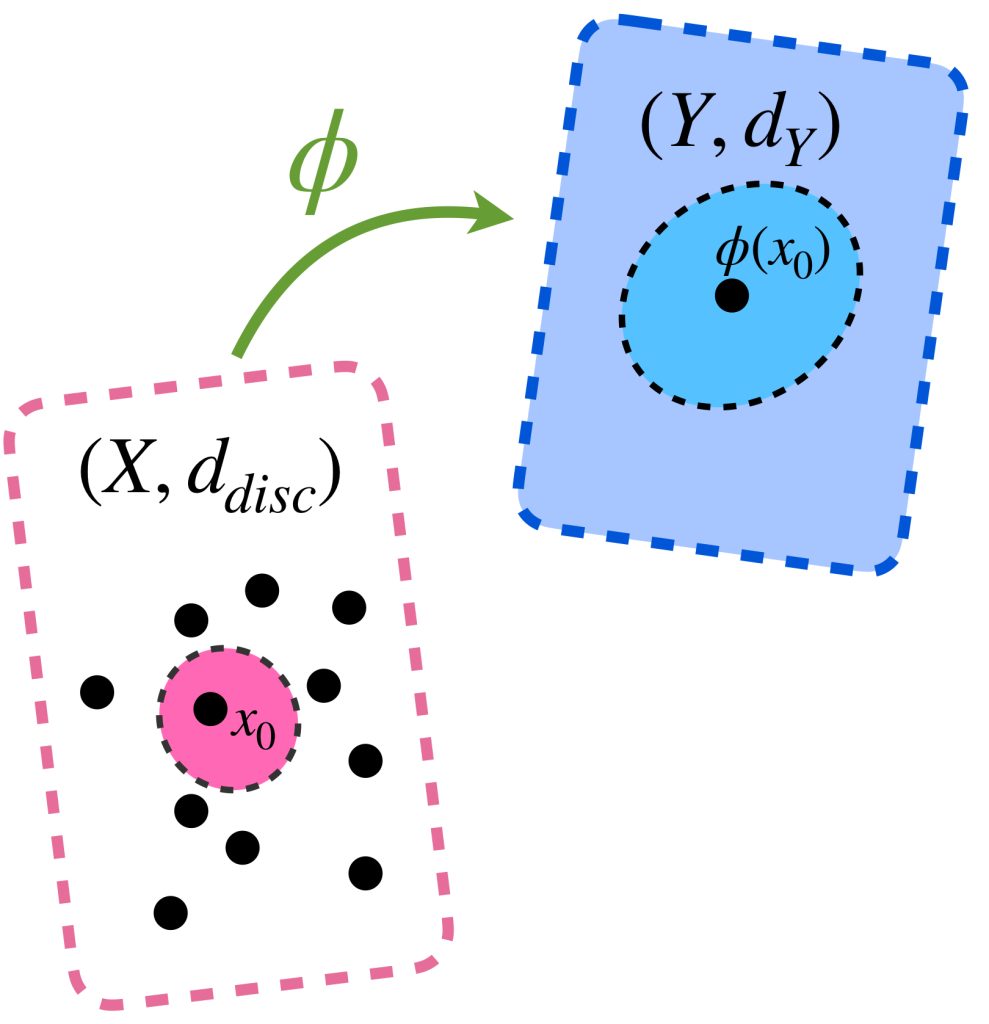
Cualquier función que tenga como dominio al espacio discreto es continua.
Demostración:
Sea $(X,d_{disc})$ el espacio discreto, $(Y,d_Y)$ espacio métrico y $\phi :X \to Y$. Sea $\varepsilon > 0$ y sea $x_0 \in X$. Entonces, si $\delta = 1$ (cualquier delta mayor que cero pero menor igual que $1$ funciona) tenemos:
$d_{disc}(x_0,x)< \delta$ entonces $x_0 = x\, $ así $\, d_Y(\phi (x_0),\phi(x))=d_Y(\phi(x_0),\phi(x_0))=0< \varepsilon.$ Por lo tanto, $\phi$ es continua en el espacio discreto $X$.
La siguiente proposición expresa la continuidad en términos de sucesiones.
Proposición. La función $\phi: X \to Y$ es continua en $x_0 \in X$ si y solo si para toda sucesión $(x_n)_{n \in \mathbb{N}} \,$ que converge en $X$ se cumple que:
$$\underset{n \to \infty}{lim} \, \phi(x_n) \, =\,\phi(\underset{n \to \infty}{lim} \, x_n).$$ La demostración se deja como ejercicio. Te sugerimos comparar esta proposición con la que concluye el límite de una función a partir de sucesiones vista en Límite de una función.
Las siguientes son propiedades de las funciones continuas:
Proposición. Sean $\phi, \psi: A \subset X \to \mathbb{C}$ funciones continuas en $x_0 \in X$, entonces:
a) $\phi(x) \pm \psi(x)$ es continua en $x_0$.
b) $\phi(x) \psi(x)$ es continua en $x_0$.
c) $\phi(x) / \psi(x)$ es continua en $x_0$ cuando $\psi(x_0) \neq 0$
La demostración se deja como ejercicio.
Proposición. Sean $\phi,\psi : A \subset X \to \mathbb{R}^n$ dos funciones continuas en $x_0 \in X$, entonces:
a)$(\phi \pm \psi)(x)$ es continua en $x_0$.
b)$(\phi \cdot \psi)(x)$ es continua en $x_0$.
c) $\lambda \phi (x)$ con $\lambda \in \mathbb{R}$ es continua en $x_0$.
La demostración se deja como ejercicio.
Antes de continuar, veamos con detenimiento la siguiente:
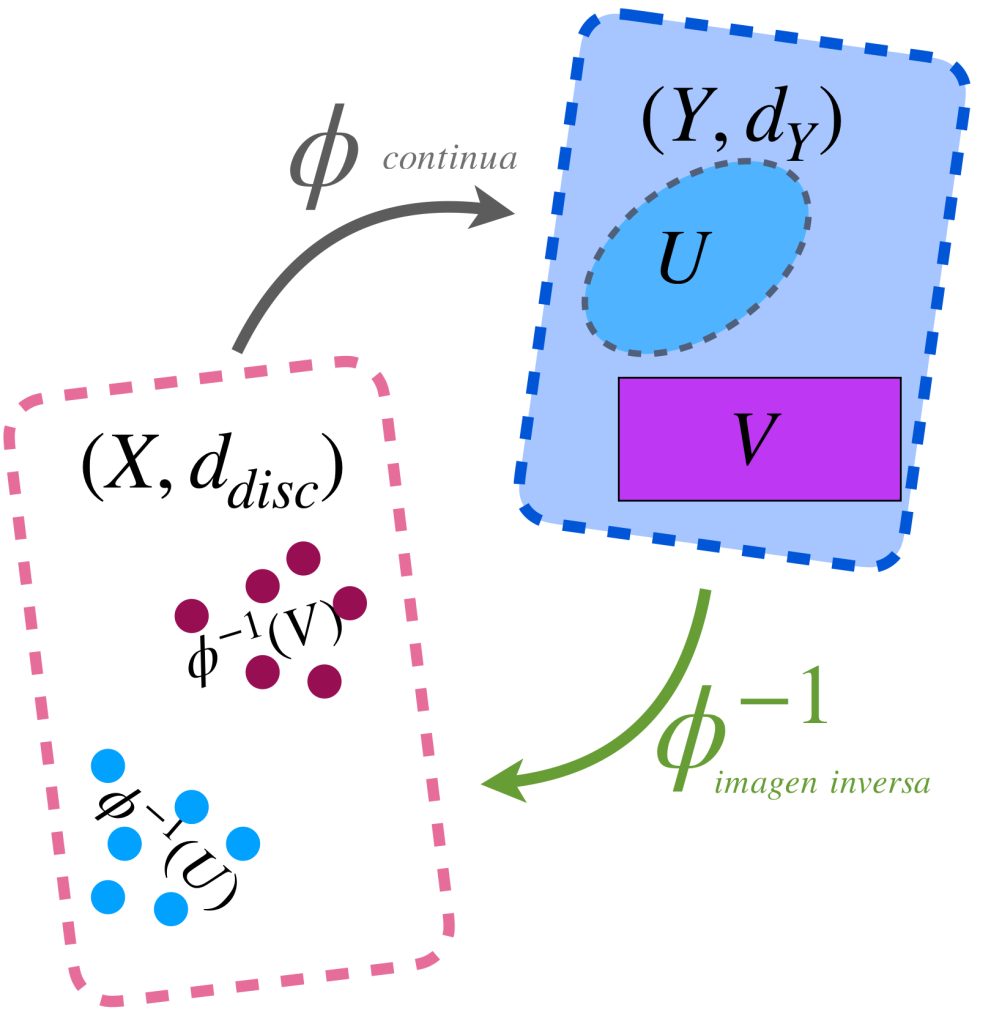
Definición. Imagen inversa. Sean $X$ y $Y$ dos conjuntos y $f:X \to Y$ una función entre ellos. Si $\, U \subset Y,$ diremos que la imagen inversa del subconjunto $U$, es el conjunto de todos los elementos de $X$ que bajo la función $f$ están en $U$. Se denota como $f^{-1}(U).$ Formalmente tenemos:
$$f^{-1}(U)=: \{x \in X : f(x) \in U\}$$
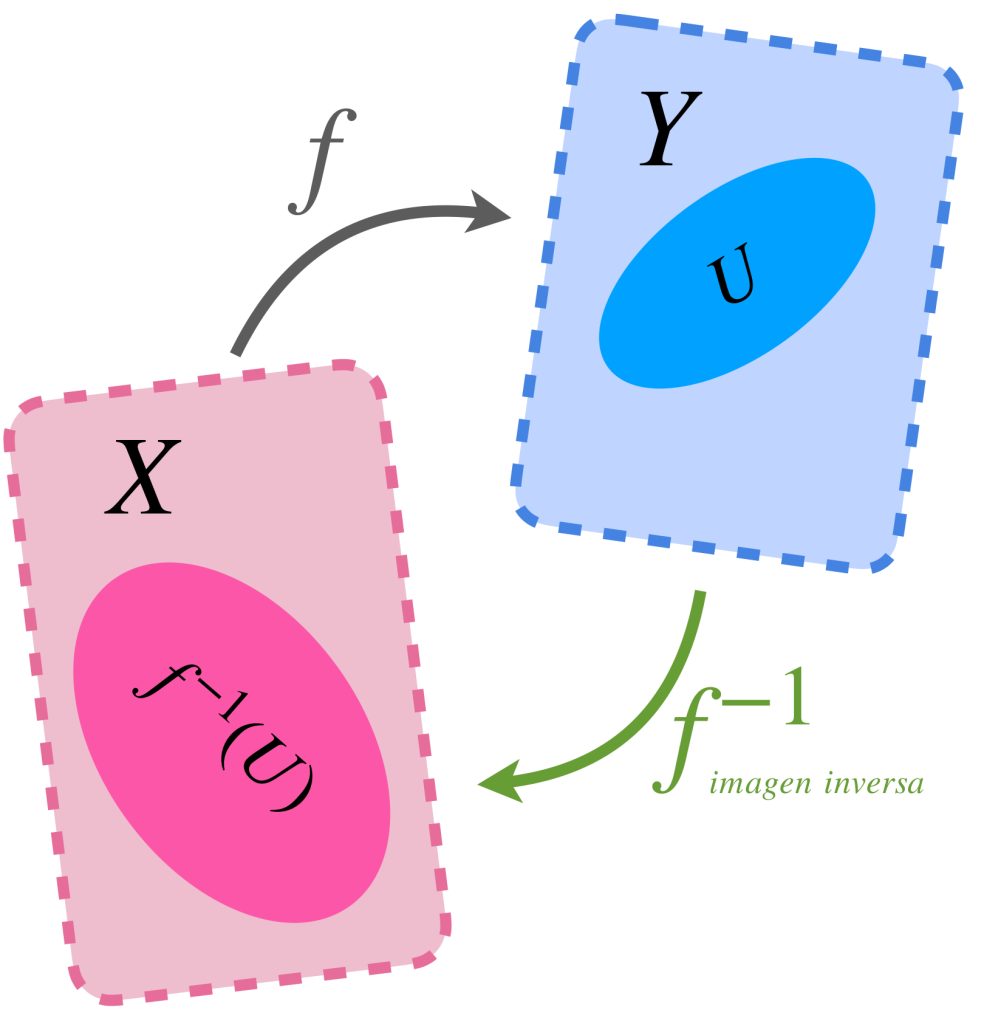
Nota: Ten cuidado de no confundir el concepto de imagen inversa $f^{-1}(U)$ (que es una forma de definir conjuntos en $X$ a partir de un conjunto en $Y$) con el concepto de la función inversa de $f$ que, aunque también se denota como $f^{-1},$ hace referencia a una función que se evalúa en puntos de $Y$ y solo existe cuando $f$ es biyectiva.
Ahora consideremos un conjunto $U_1 \subset X.$ La función $f$ define en $Y$ el conjunto $f(U_1)$. Si renombramos a este conjunto como $\, U_2 \,$ y buscamos identificar ahora la imagen inversa de este nuevo conjunto, ¿regresaremos al mismo conjunto $\, U_1$ del cual partimos? Observa que, dependiendo la naturaleza de la función, es posible que la imagen inversa nos arroje un conjunto más grande que el $\, U_1 \,$ inicial, sin embargo $\, U_1 \,$ estará contenido.
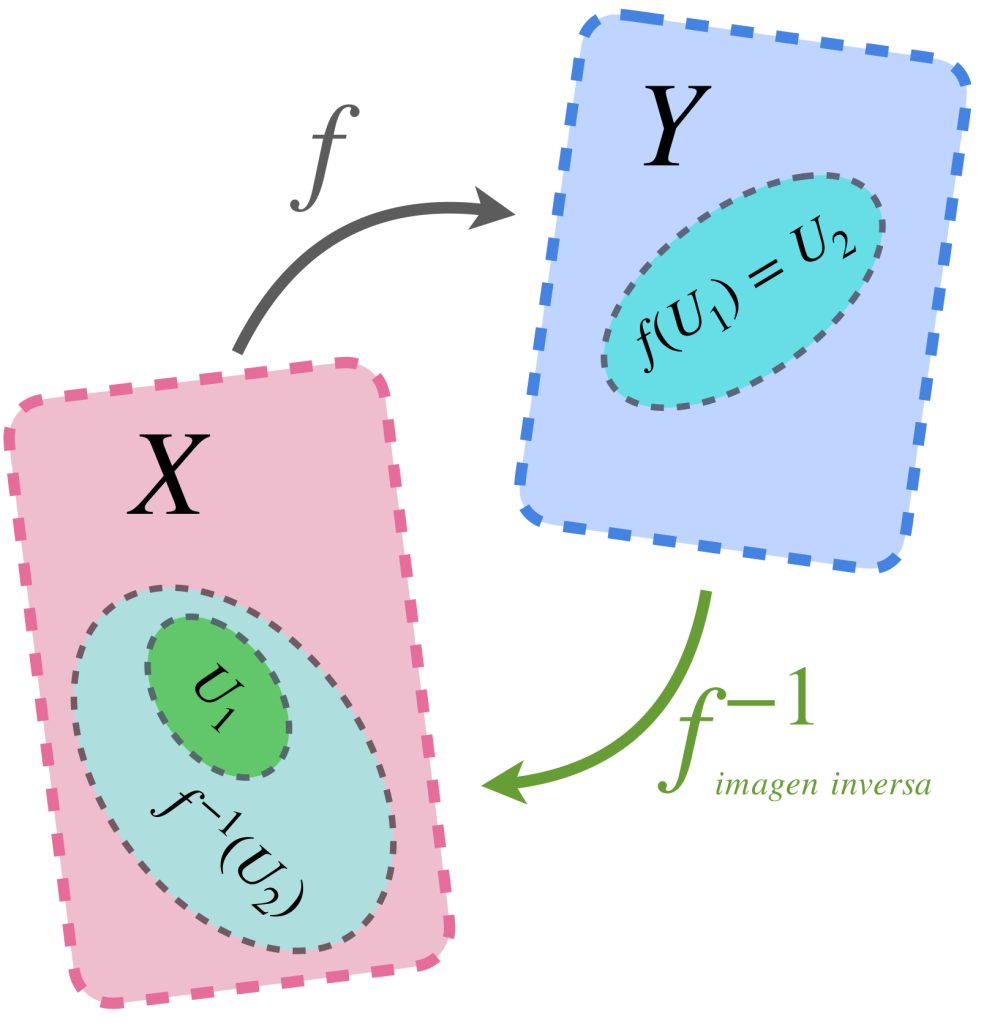
Esto ocurre porque es posible que haya puntos en $\, U_2 \,$ que son igualmente asignados por la función $f$ para puntos fuera de $\, U_1 \,$.
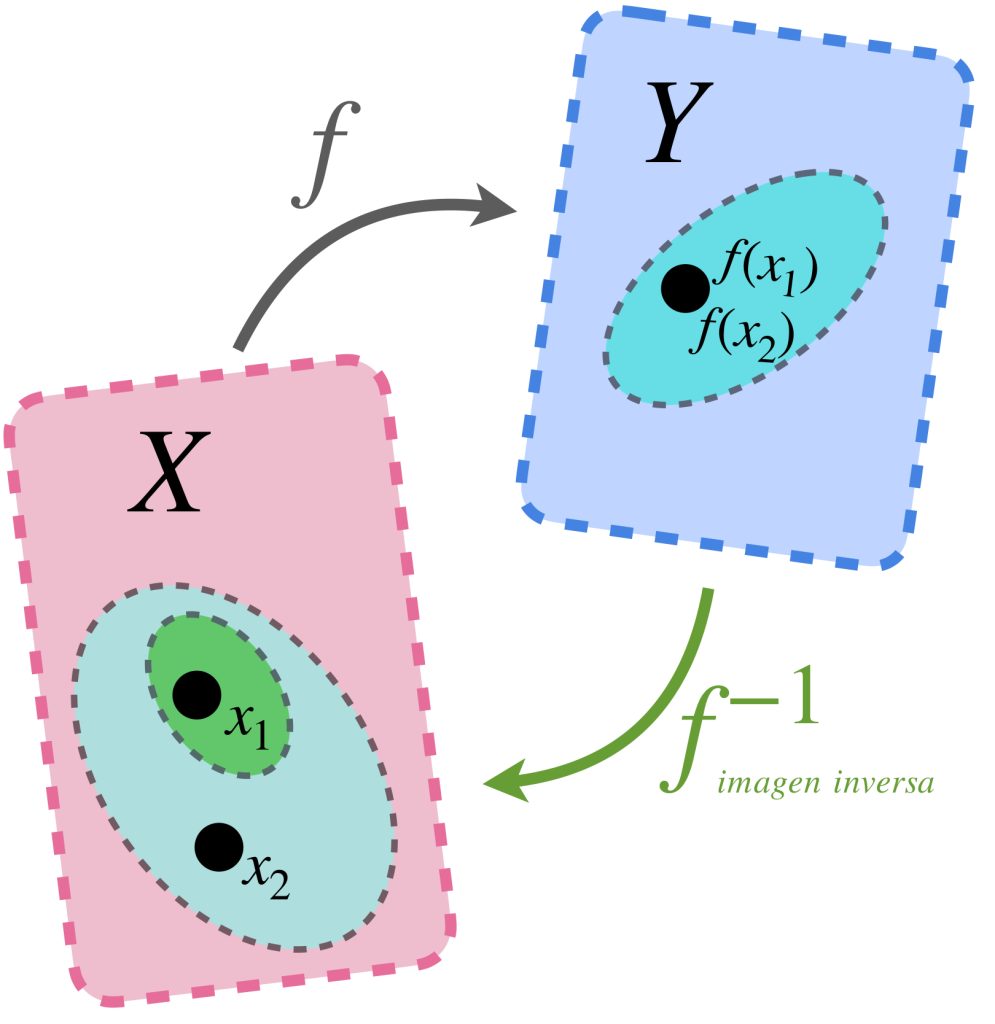
¿Bajo qué condiciones no pasaría esto?
Para finalizar esta sección, veamos las siguientes propiedades de las funciones continuas:
Proposición. Sean $X$ y $Y$ espacios métricos y $\phi:X \to Y$ una función. Las siguientes afirmaciones son equivalentes:
a) $\phi: X \to Y$ es continua.
b) Para todo subconjunto abierto $U \subset Y$, $\phi^{-1}(U)$ es un conjunto abierto en $X.$
c) Para todo subconjunto cerrado $V \subset Y$, $\phi^{-1}(V)$ es un conjunto cerrado en $X.$
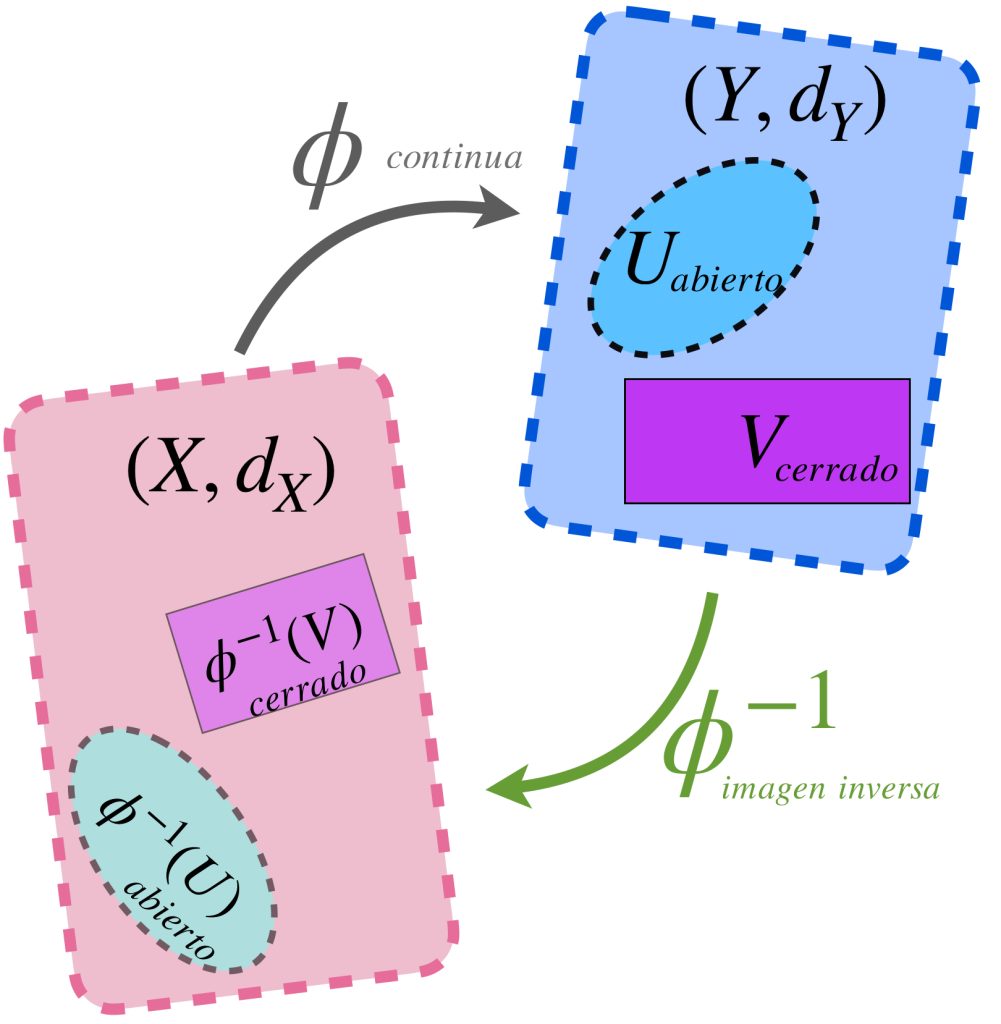
Demostración:
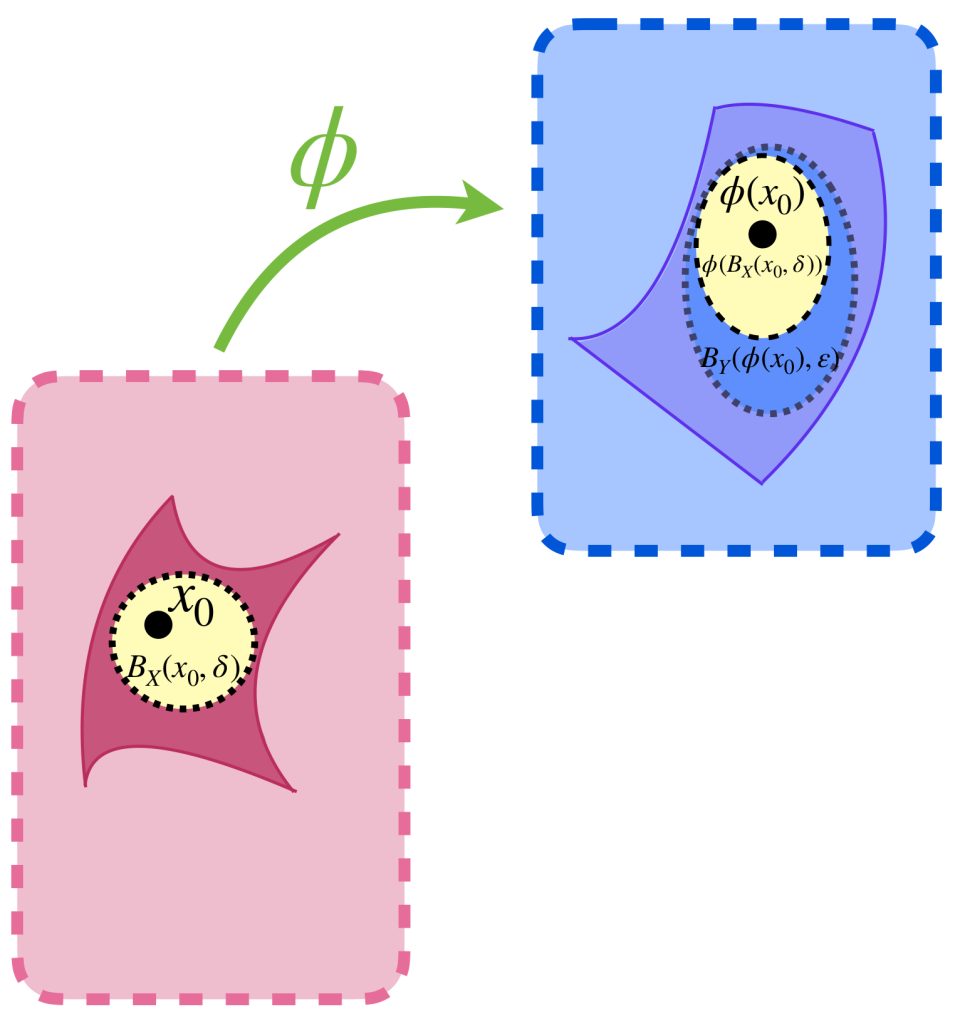
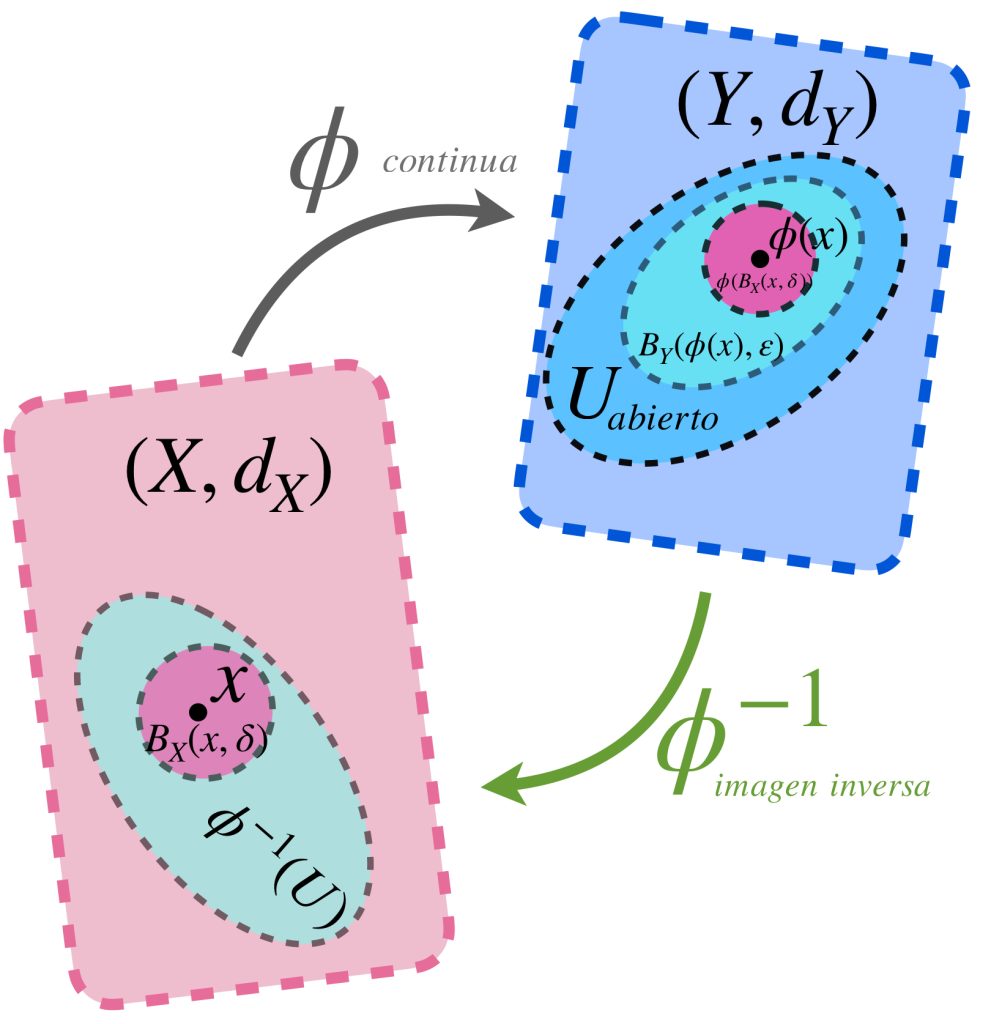
Para probar a) $\Rightarrow$ b) considera $U \subset Y$ abierto y $\, x \in \phi^{-1}(U).$ Entonces existe $\varepsilon >0$ tal que $B_Y(\phi(x), \varepsilon) \subset U$, pues $U$ es abierto. Como $\phi$ es continua en $x$, entonces existe $\, \delta >0$ tal que $\phi (B_X(x, \delta)) \subset B_Y(\phi(x), \varepsilon) \subset U.$ Por lo tanto $B_X(x, \delta)) \subset \phi^{-1}(U) \,$ lo que demuestra que $\phi^{-1}(U)$ es un conjunto abierto en $X.$
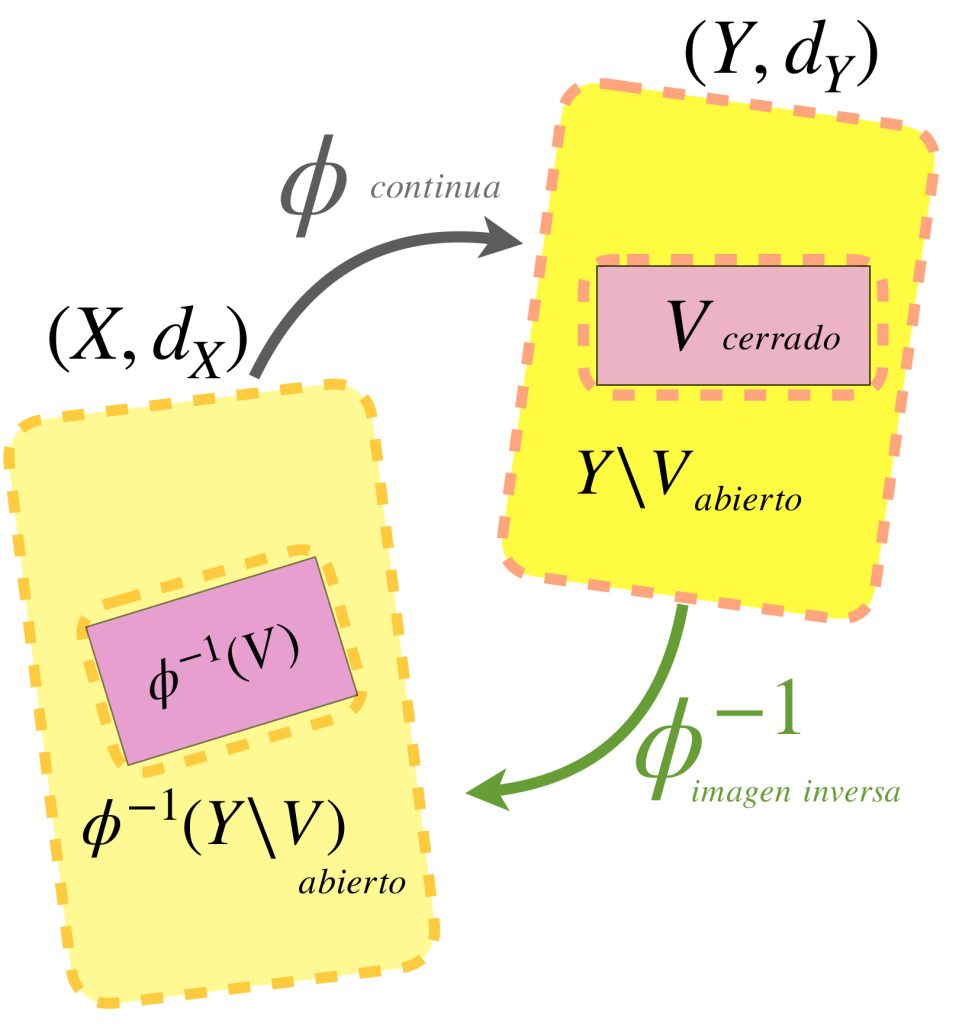
Para probar b) $\Rightarrow$ c) considera $V \subset Y$ cerrado. Entonces $Y \setminus V$ es abierto en $Y$. Así $\phi ^{-1}(Y \setminus V)$ es abierto en $X$ de modo que $X \setminus \phi ^{-1}(Y \setminus V)$ es cerrado en $X$.
Nota que $\phi^{-1}(V)=X \setminus \phi ^{-1}(Y \setminus V)$ pues $x \in \phi^{-1}(V) \,$ $\Leftrightarrow$ $\phi(x) \in V$ $\Leftrightarrow$ $\phi(x) \notin (Y \setminus V)$ $\Leftrightarrow$ $x \notin \phi ^{-1}(Y \setminus V)$ $\Leftrightarrow$ $x \in X \setminus \phi ^{-1}(Y \setminus V)$. Por lo tanto $\phi^{-1}(V)$ es cerrado en $X.$
Para probar c) $\Rightarrow$ a) considera $x \in X$. Sea $\varepsilon>0$ entonces la bola $B_Y(\phi(x),\varepsilon)$ es abierto por lo tanto su complemento $Y \setminus B_Y(\phi(x),\varepsilon)$ es cerrado. Por hipótesis, la imagen inversa dada por $\phi^{-1}(B_Y(\phi(x),\varepsilon))$ es un conjunto cerrado en $X$. En consecuencia el complemento de $\phi^{-1}(B_Y(\phi(x),\varepsilon))$ es un conjunto abierto en $X$ que tiene a $x$ como elemento. Llamemos $U$ a este conjunto.
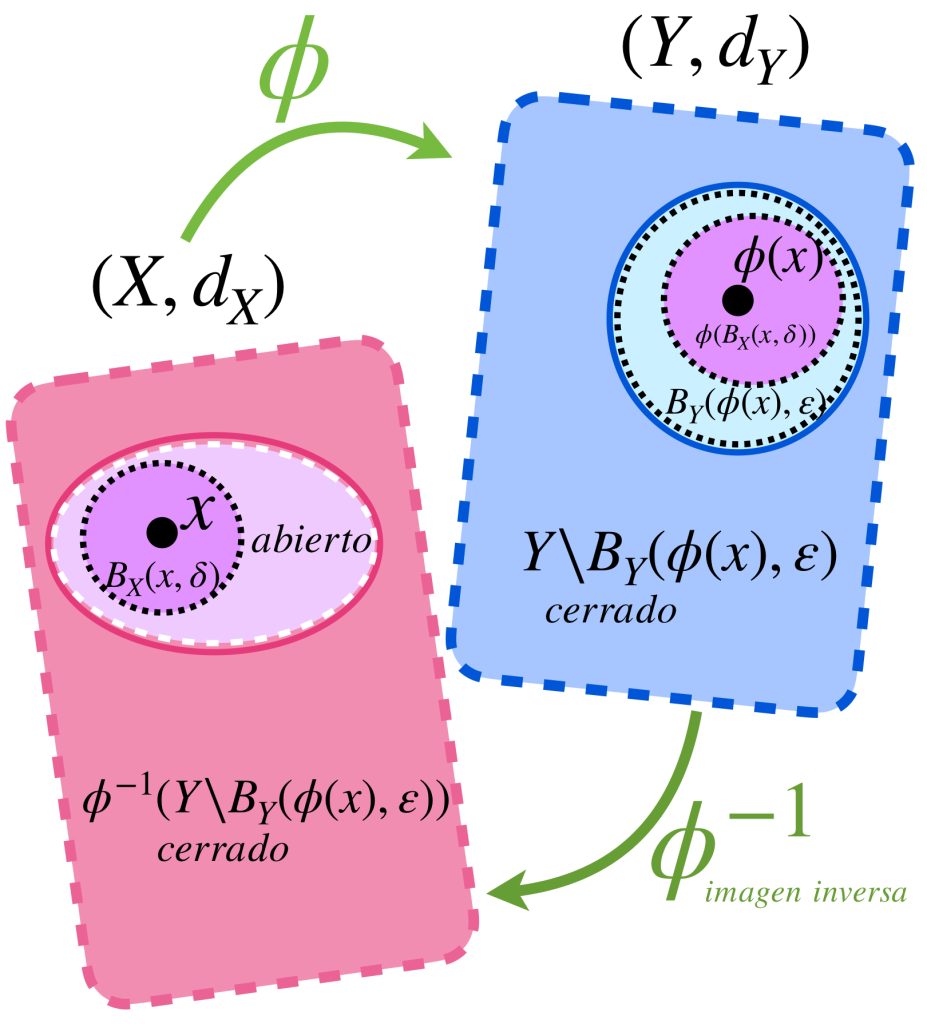
Como $U$ es abierto, existe $\delta>0$ tal que $B_X(x,\delta) \subset U$. Por lo tanto la imagen $f(B_X(x,\delta)) \subset B_Y(\phi(x),\varepsilon)$ lo que prueba que la función $\phi$ es continua en $x$. Como $x$ fue arbitrario, se concluye que $\phi$ es continua en el espacio $X$.
Más adelante…
Veremos cómo la existencia de funciones continuas entre dos espacios muestra propiedades que se conservan en ambos. Ya no hablaremos solo de la cercanía a los puntos, sino que haremos esa distancia más específica y comparable a la registrada en el espacio del dominio. Conoceremos así a los espacios isomorfos y homeomorfos.
Tarea moral
- Demuestra que la función $\phi: X \to Y$ es continua en $x_0 \in X$ si y solo si para toda sucesión $(x_n)_{n \in \mathbb{N}}$ que converge en $X$ se cumple que:
$$\underset{n \to \infty}{lim} \, f(x_n) \, =\,f(\underset{n \to \infty}{lim} \, x_n)$$. - Demuestra que si $\phi, \psi: A \subset X \to \mathbb{C}$ son funciones continuas en $x_0 \in X$, entonces:
a) $\phi(x) \pm \psi(x)$ es continua en $x_0$.
b) $\phi(x) \psi(x)$ es continua en $x_0$.
c) $\phi(x) / \psi(x)$ es continua en $x_0$ cuando $\psi(x_0) \neq 0$ - Demuestra que si $\phi,\psi : A \subset X \to \mathbb{R}^n$ son dos funciones continuas en $x_0 \in X$, entonces:
a)$(\phi \pm \psi)(x)$ es continua en $x_0$.
b)$(\phi \cdot \psi)(x)$ es continua en $x_0$.
c) $\lambda \phi (x)$ con $\lambda \in \mathbb{R}$ es continua en $x_0$. - Usa la última proposición de esta sección para probar que cualquier función que tenga como dominio al espacio discreto es continua.
- ¿Es posible concluir que cualquier función que tenga como contradominio al espacio discreto es continua?