Introducción
En la entrada anterior vimos que no es suficiente que una sucesión sea de Cauchy para asegurar que sea convergente. Hay espacios donde sí lo es y serán llamados «completos». Contar con este recurso nos permite solo tener que justificar que una sucesión satisface la condición de Cauchy cuando esto resulte ser más sencillo que demostrar su convergencia en un punto. Comencemos con la definición:
Definición espacio métrico completo y espacio de Banach: Sea $(X,d)$ un espacio métrico. Decimos que $X$ es un espacio métrico completo si toda sucesión de Cauchy $(x_n)_{n \in \mathbb{N}}$ es convergente en $X$.
A un espacio normado que es completo con la métrica inducida por su norma le llamaremos espacio de Banach.
Ejemplos:
- El espacio métrico euclideano $\mathbb{R}^n$ es completo. La demostración la vimos en la sección anterior. (Sucesiones de Cauchy).
- Sea $X$ un conjunto no vacío con la métrica discreta. Entonces $X$ es completo. La demostración se propondrá como ejercicio.
- $\mathbb{R}^n$ con la métrica $d_\infty(x,y)=máx \{ |x_1-y_1|,…,|x_n-y_n| \}$ donde $x=(x_1,…,x_n)$ y $y=(y_1,…,y_n)$ es completo.
Demostración:
Sea $(x_n)_{n \in \mathbb{N}}$ una sucesión de Cauchy en $\mathbb{R}^n$. En la sección anterior vimos que $(x_n)$ converge en la métrica euclidiana $d_2$. Sea $x$ el punto de convergencia. En la entrada Más conceptos de continuidad vimos que $d_\infty$ y $d_2$ son métricas equivalentes, entonces para todo $\varepsilon >0$ existe $N \in \mathbb{N}$ y $c>0$ tales que para todo $n \geq N$:
$d_\infty(x_n,x)\leq c\,d_{2}(x_n,x) \leq c \frac{\varepsilon}{c}=\varepsilon$
Por lo tanto $x_n \to x$ en $(\mathbb{R}^n, d_\infty),$ lo cual demuestra que es un espacio métrico completo.
En general, la completitud no es una propiedad invariante bajo homeomorfismos. Esto es, un espacio completo puede ser homeomorfo a otro que no lo sea.
Ejemplo: El espacio euclidiano $\mathbb{R}$ es homeomorfo al subespacio $(-1,1).$
En efecto:
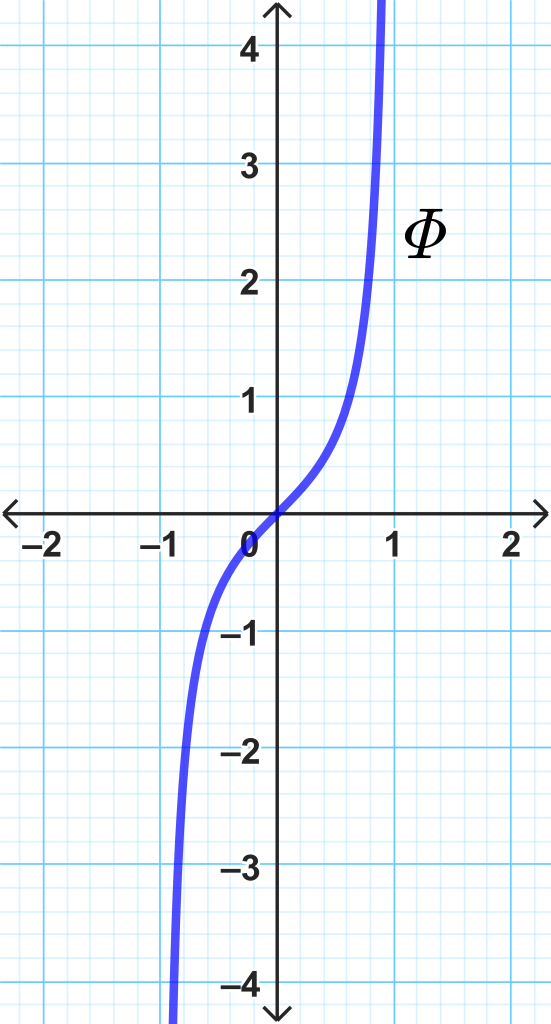
$$ \phi: (-1,1) \longrightarrow \mathbb R, \qquad \phi(x) = \frac{x}{1-x^2} $$
Es un homeomorfismo entre ambos espacios. No obstante la sucesión $(1- \frac{1}{n})_{n \in \mathbb{N}} \,$ tiene sus elementos en $(-1,1)$ y es de Cauchy pero no converge en el subespacio. Por lo tanto $(-1,1)$ no es completo pese a que $\mathbb{R}$ sí lo es.
Por otro lado, la completitud sí se conserva bajo equivalencias. (Concepto visto en Más conceptos de continuidad):
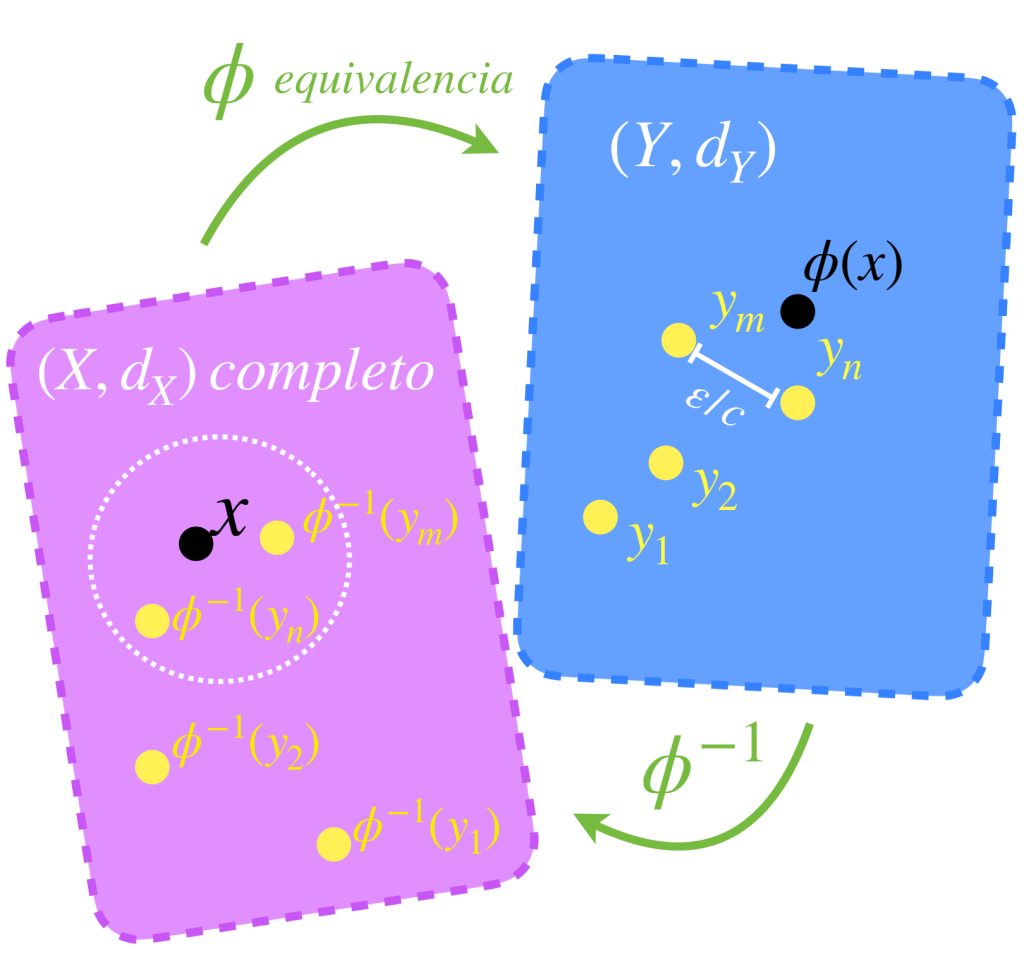
Proposición: Sean $(X,d_X)$ y $(Y,d_Y)$ espacios métricos con $\phi: X \to Y$ una equivalencia entre ellos. Entonces $X$ es completo si y solo si $Y$ lo es.
Demostración:
Supongamos que $X$ es completo. Buscamos demostrar que $Y$ también lo es. Sea $(y_n)_{n \in \mathbb{N}}$ una sucesión de Cauchy en $Y$. Como $\phi$ es equivalencia entonces $\phi^{-1}$ es lipschitz continua. Considera la sucesión $\phi^{-1}(y_n)_{n \in \mathbb{N}}$ en $X$. Dadas las hipótesis, para toda $\varepsilon >0$ existe $N \in \mathbb{N}$ y $c>0$ tales que si $n,m \geq N$ entonces:
$d_X(\phi^{-1}(y_n),\phi^{-1}(y_m))\leq c\, d_Y(y_n,y_m) \leq c \, \frac{\varepsilon}{c} = \varepsilon$ lo cual prueba que la sucesión $\phi^{-1}(y_n)_{n \in \mathbb{N}}$ es de Cauchy en $X$, espacio que es completo, en consecuencia $\phi^{-1}(y_n) \to x$ en $X$ para algún $x \in X.$
Finalizamos aplicando $\phi$ a la última sucesión. En la entrada de Funciones continuas en espacios métricos vimos que podemos concluir que $\phi(\phi^{-1}(y_n)) \to \phi(x)$ en $Y$. Por lo tanto $(y_n)$ es una sucesión convergente lo cual demuestra que $Y$ es un espacio métrico completo.
El regreso es análogo y se propondrá como ejercicio al final de esta sección.
Proposición: Todo espacio normado de dimensión finita es de Banach.
Demostración:
Sea $V$ un espacio con norma asociada $\norm{\cdot}_V$ con dimensión finita $n$. En la entrada anterior probamos que el espacio euclideano $\mathbb{R}^n$ es de Banach. En la entrada Más conceptos de continuidad probamos que la norma $\norm{\cdot}_2$ es equivalente a $\norm{\cdot}_1$. De acuerdo a la proposición anterior, bastará con encontrar una equivalencia entre $(\mathbb{R}^n,\norm{\cdot}_1)$ y $(V, \norm{\cdot}_V)$.
Sea $\{e_1,…,e_n\}$ la base canónica de $\mathbb{R}^n,$ $\{v_1,…,v_n\},$ una base ordenada de $V$ y $\mathcal{L}: \mathbb{R}^n \to V$ tal que para cada $i=1,…,n, \, \mathcal{L}(e_i)=v_i.$ Es sencillo demostrar que $\mathcal{L}$ es una transformación lineal y que es también una función biyectiva. Esta afirmación se propondrá como ejercicio.
Sean $a,b \in \mathbb{R}^n$ tales que $a=\sum_{i=1}^{n}a_i e_i$ y $b=\sum_{i=1}^{n}b_i e_i$ con $a_i,b_i \in \mathbb{R}, 1\leq i\leq n.$ Sea $c=\underset{1 \leq i \leq n}{máx} \, \{ \norm{v_i}_V\},$ entonces:
\begin{align*}
\norm{\mathcal{L}(\sum_{i=1}^{n}a_i e_i) -\mathcal{L}(\sum_{i=1}^{n}b_i e_i)}_V&=\norm{\sum_{i=1}^{n}a_i \mathcal{L}(e_i)-\sum_{i=1}^{n}b_i \mathcal{L}(e_i)}_V\\
&=\norm{\sum_{i=1}^{n}a_i v_i-\sum_{i=1}^{n}b_i v_i}_V\\
&=\norm{\sum_{i=1}^{n}(a_i-b_i) v_i}_V \\
&\leq \sum_{i=1}^{n}|a_i-b_i| \norm{v_i}_V \\
&\leq \underset{1 \leq i \leq n}{máx} \, \{ \norm{v_i}_V\}\sum_{i=1}^{n}|a_i-b_i|\\
&=c \sum_{i=1}^{n}|a_i-b_i| \\
&=c \norm{a-b}_1
\end{align*}
Entonces $\mathcal{L}$ es una función Lipschitz continua. La prueba de que la inversa es Lipschitz continua se deja como ejercicio. Esto demostraría que $V$ también es un espacio de Banach.
La completitud no siempre se hereda a los subespacios de un espacio métrico completo. La siguiente proposición nos muestra las condiciones requeridas para que esto ocurra:
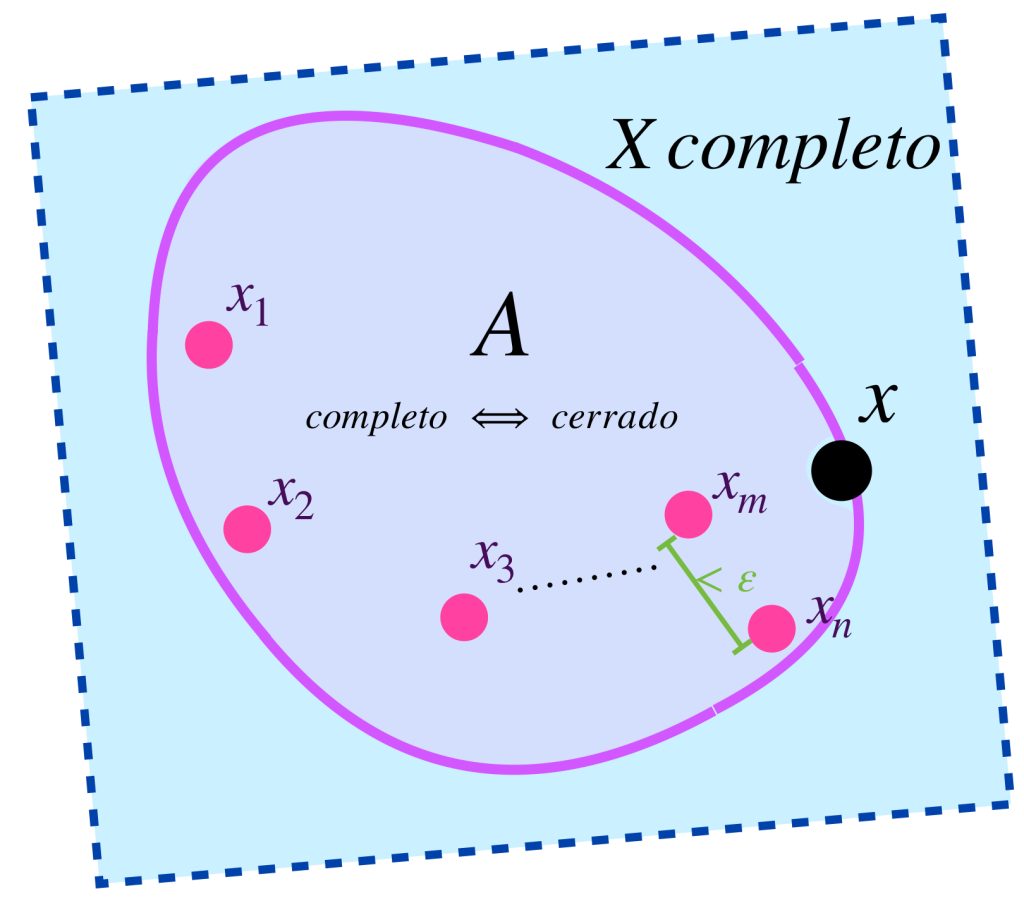
Proposición: Sea $(X,d)$ un espacio métrico completo y $A \subset X.$ Entonces el subespacio $(A,d)$ es completo si solo si $A$ es cerrado en $X.$
Demostración:
Supón que $(A,d)$ es completo. Buscamos demostrar que $\overline{A} \subset A.$ Sea $x \in \overline{A}.$ En la entrada de Convergencia concluimos que existe una sucesión $(x_n)_{n \in \mathbb{N}}$ de términos en $A$ tal que $x_n \to x.$ Como converge, se concluye que es de Cauchy. Como todos los términos están en $A$, que es completo, se concluye que es convergente en $A.$ Como el límite es único, concluimos que el punto de convergencia $x \in A.$ Por lo tanto $\overline{A} \subset A,$ probando así que $A$ es cerrado.
Ahora partamos de suponer que $A \subset X$ es cerrado. Sea $(x_n)_{n \in \mathbb{N}}$ una sucesión de Cauchy en $A.$ Como $X$ es completo, se sigue que $x_n \to x$ en $X$ para algún $x \in X.$ Por el mismo resultado de la entrada de Convergencia concluimos que $x \in A.$ por lo tanto $x_n \to x$ en $A$ lo cual demuestra que $A$ es completo.
Ya que sabemos que un espacio normado de dimensión finita es de Banach, es natural preguntarse qué ocurre con los de dimensión infinita. Como ejemplo tenemos al espacio de los polinomios $\mathcal{P}[0,1].$ Visto como subespacio del espacio de funciones continuas $C^0[0,1]$ es de dimensión infinita pero no es cerrado. La proposición anterior nos permite concluir que $\mathcal{P}[0,1]$ no es completo. La demostración del ejemplo se puede consultar en las notas de Luis O. Manuel. El documento se encuentra en este link.
Más adelante…
Buscaremos aplicar estos resultados en conjuntos anidados, unos dentro de otros. Partir de una sucesión de Cauchy nos permitirá asegurar la existencia de un punto de convergencia, cuando estemos en un espacio completo. Conoceremos condiciones en las que dicho punto existe y pertenece a la intersección de los conjuntos anidados.
Tarea moral
- Demuestra que si $X$ es un conjunto no vacío con la métrica discreta entonces $X$ es completo.
- Sean $(X,d_X)$ y $(Y,d_Y)$ espacios métricos con $\phi: X \to Y$ una equivalencia entre ellos. Prueba que si $Y$ es completo entonces $X$ lo es.
- Sea $V$ un espacio con norma asociada $\norm{\cdot}_V$ con dimensión finita $n$ y $\{v_1,…,v_n\},$ una base ordenada de $V.$ Sea $\{e_1,…,e_n\}$ la base canónica de $\mathbb{R}^n,$ y $\mathcal{L}: \mathbb{R}^n \to V$ tal que para cada $i=1,…,n, \, \mathcal{L}(e_i)=v_i.$ Demuestra que $\mathcal{L}$ es una transformación lineal y que es también una función biyectiva.
- Prueba que la función inversa de la función del ejercicio anterior es Lipschitz continua.
- Sea $(x_n)_{n \in \mathbb{N}}$ una sucesión creciente y acotada en $\mathbb{R}.$ Concluye que $(x_n)$ es convergente en $\mathbb{R}$ demostrando que es de Cauchy.