$ \textit{ MATERIAL EN REVISIÓN}$
Introducción
«Desde un punto de vista intuitivo, un espacio métrico es, simplemente, un conjunto en donde podemos hablar de la distancia entre sus elementos, lo que nos permitirá precisar la noción de «proximidad», una idea que está presente implícitamente en todos los conceptos fundamentales de la Topología y el Análisis.
Como estructura matemática abstracta, el concepto de espacio métrico fue introducido inicialmente por el matemático francés M.Fréchet en 1906. Probó que las ideas de Cantor de subconjuntos abiertos y cerrados podían extenderse de manera natural a los espacios métricos. Más tarde, el concepto fue desarrollado por F. Hausdorff en su Mengenlehre. En parte, su importancia radica en que constituye una interesante generalización de los espacios normados, cuya teoría fue básicamente desarrollada por Stephan Banach como cimiento del Análisis Funcional. El desarrollo posterior de las investigaciones sobre topología métrica ha puesto de manifiesto su extraordinario poder para unificar una amplia variedad de teorías hasta entonces dispersas y aparentemente independientes». (Díaz, 1998).

(1878-1973)
Fuente: Laurent Mazliak (LPSM).

(1845-1918)
Fuente: Maths Society Ventures.

(1868,1942)
Fuente: Carlos Prieto / UNAM

(1892,1945)
Fuente: Efemérides Matemáticas – UNAM
¿Qué es un espacio métrico?
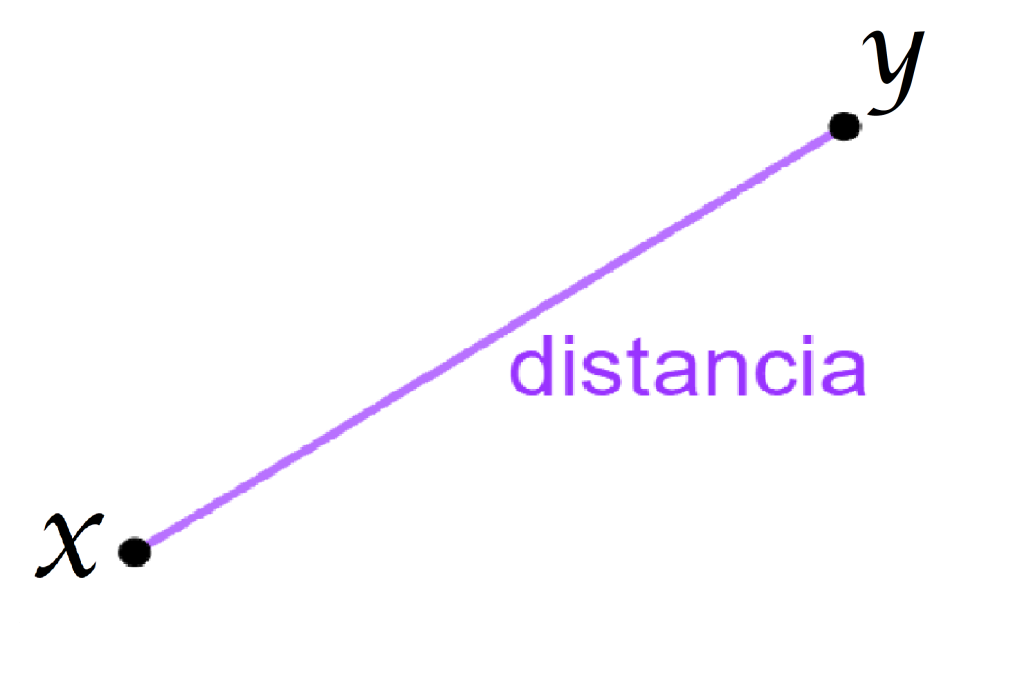
Pensemos en un conjunto de elementos que representamos como puntos. Supongamos que cada vez que tomamos dos puntos cualesquiera del conjunto podemos hablar de la distancia que hay entre ellos (como un valor numérico específico), entonces tenemos un espacio métrico cuando se cumplen ciertas condiciones.
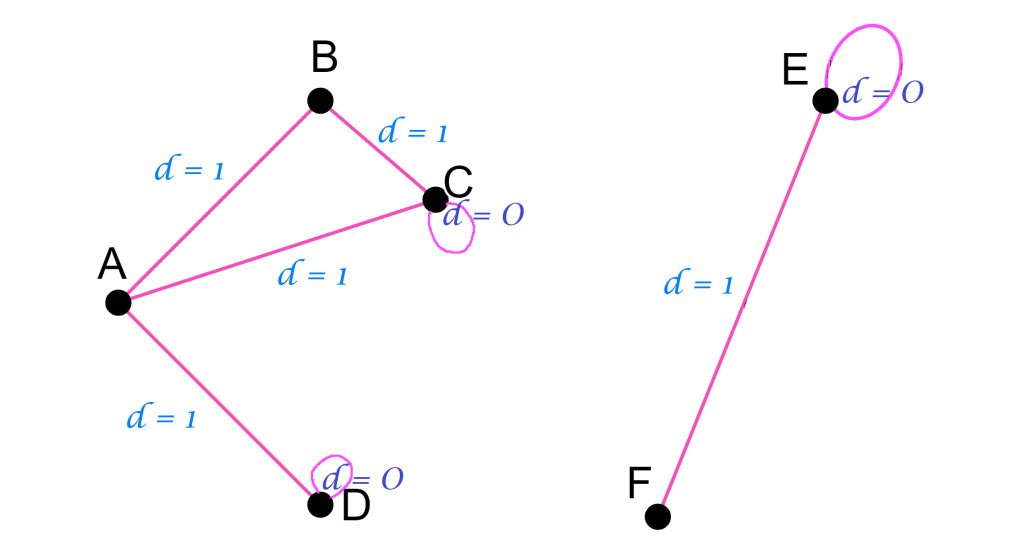
Como representación de la idea de distancia observa el siguiente esquema. Aunque en él se muestran solo algunas de las distancias entre dos puntos, esta debe estar definida entre cualquier par del conjunto. Nota que la distancia del punto $E$ a sí mismo es $0$. Así lo será también la distancia de cualquier otro punto a sí mismo.
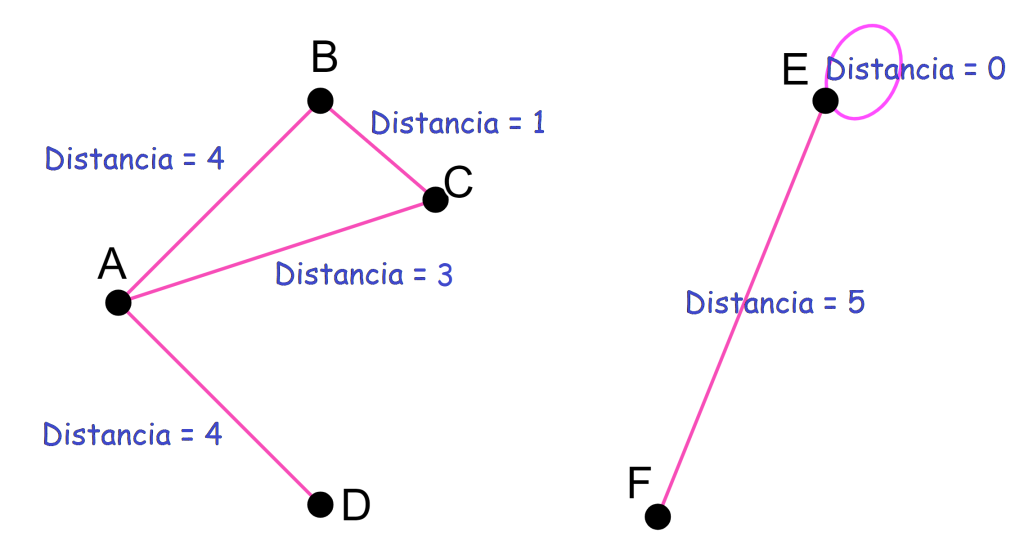
La distancia cumplirá lo siguiente:
- La distancia de un punto a sí mismo será $0$. La distancia entre puntos distintos será distinta de $0$.
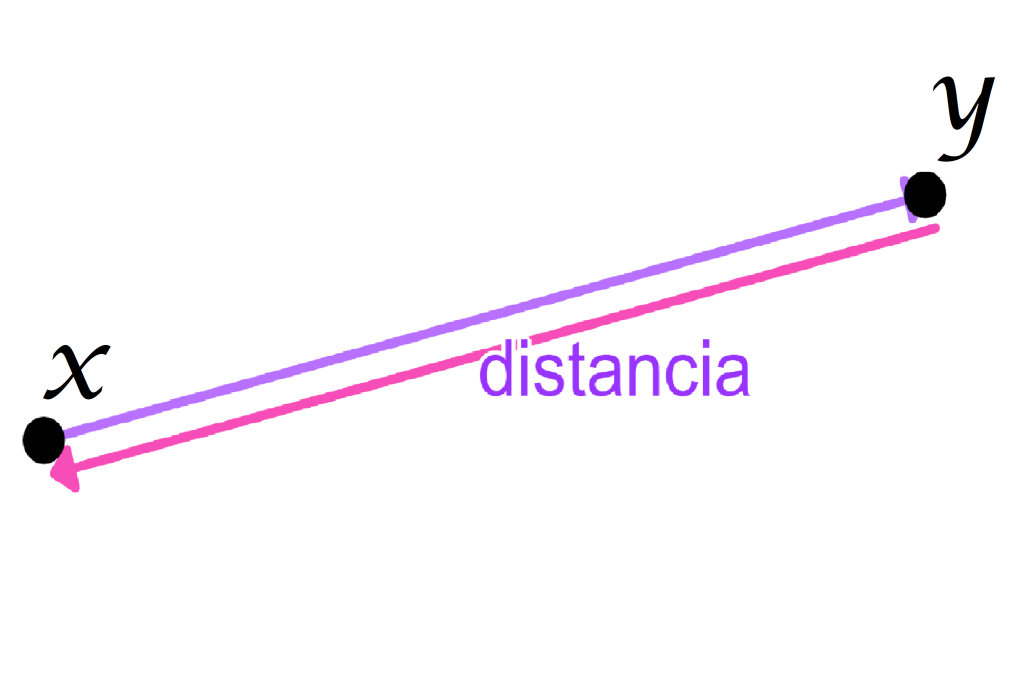
- En un espacio métrico la distancia entre dos puntos es simétrica. Esto significa que la distancia entre el punto $x$ y $y$ coincide con la distancia entre el punto $y$ y $x$.
Aunque esto parezca difícil de contradecir, ¿puedes mencionar un ejemplo en tu vida cotidiana en el que el camino que sigues para llegar a un lugar no coincida con el de regreso? Probablemente esto marcará diferencias en los metros recorridos y quizá también en el tiempo o el costo del traslado.
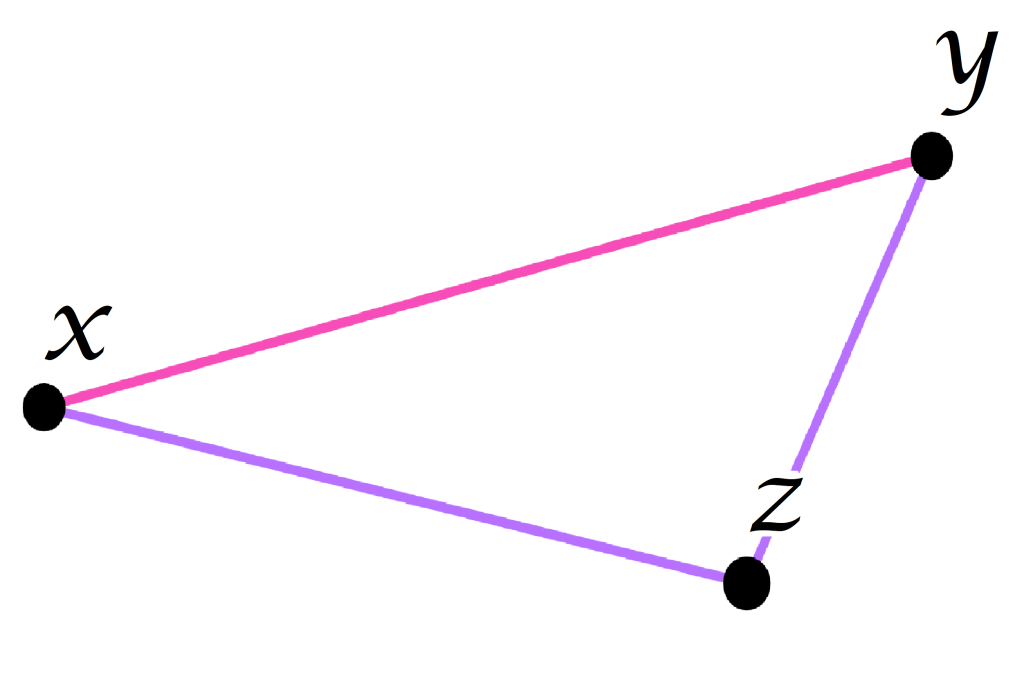
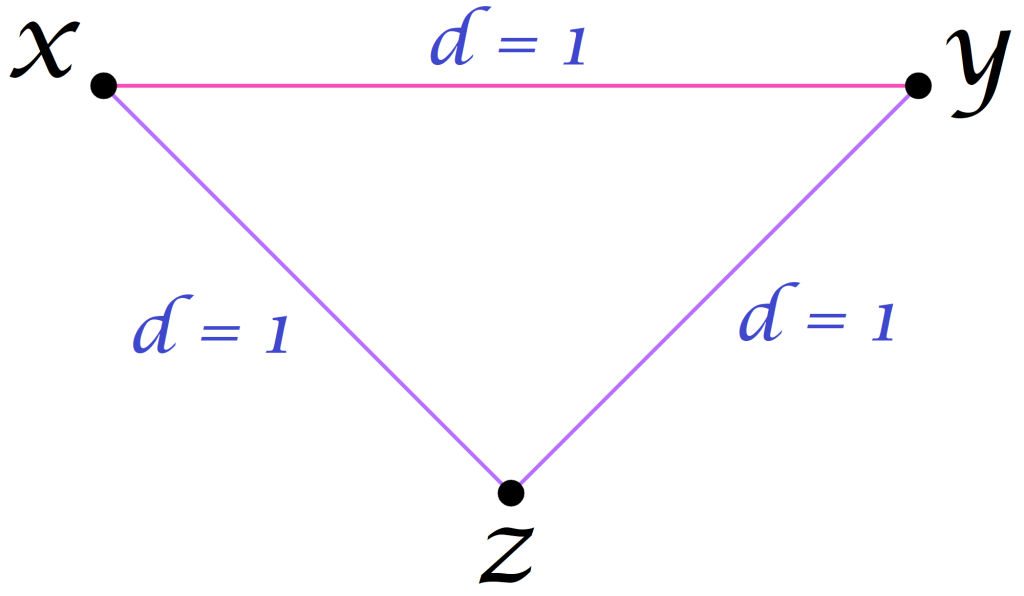
- Entre cualesquiera tres puntos se satisface la desigualdad del triángulo. Decimos que la suma de dos de las distancias entre los vértices de un triángulo es mayor o igual que la distancia restante.
De manera formal, tenemos lo siguiente:
Definición. Espacio métrico. Un espacio métrico $(X,d)$ es un par ordenado donde $X$ es un conjunto no vacío, (cuyos elementos llamaremos puntos) y $d$ es la métrica asociada a este.
Definición. Métrica. Llamaremos métrica o distancia en $X$ a una relación $d: X \times X \to \mathbb{R}$ que satisface los siguientes tres axiomas para cualesquiera $x$, $y$, $z$ $\in X$:
\[
\begin{align}
& d(x,y)=0 \quad\text{si y solo si}\quad x = y \\
& d(x,y) = d(y,x) \\
& d(x,y) \leq d(x,z) + d(z,y)
\end{align}
\]
Nota: La distancia nunca es negativa. De estos axiomas se deduce que si $x \neq y$ entonces $0<d(x,y)$ pues:
\begin{align*}
0 &= d(x,x)\\
&\leq d(x,y) + d(y,x)\\
&= d(x,y) + d(x,y)\\
&= 2d(x,y)
\end{align*}
Luego de multiplicar por $\dfrac{1}{2}$ ambos lados, se deduce que $0 \leq d(x,y)$. Como $x \neq y$ concluimos a partir del axioma $(1)$ que $0<d(x,y)$.
Naturalmente estaremos pensando en la forma en que usualmente medimos las distancias a nuestro alrededor. ¿Sí satisfacen la definición de métrica estos métodos convencionales? ¿Habrá otras maneras de asignar distancias?
Ejemplos de espacios métricos
La métrica discreta
Sea $X$ un conjunto no vacío. Si para cualesquiera $x, y \in X$ definimos $d:X \times X \to \mathbb{R}$ como:
\[
d(x,y):= \left\{\begin{array}{lcc}
0 & si & x = y \\
\\ 1 & si & x \neq y
\end {array}
\right.
\]
Entonces $d$ es una métrica en $X. \, $ En este caso $(X,d)$ recibe el nombre de espacio discreto. Denotaremos este espacio como $(X,d_{disc}).$
Demostración: Sean $x, y, z \in X$. El axioma $(1)$ se cumple por definición.
Para demostrar el axioma $(2)$ veamos que si $x = y$ entonces $d(x,y) = 0 = d(y,x)$. Por otro lado, si $x \neq y$ entonces $d(x,y) = 1 = d(y,x)$. En cualquier caso $d(x,y) = d(y,x)$.
Para demostrar $(3)$ veamos que si $x=y$ entonces $d(x,y)=0$. Como las distancias siempre son mayores o iguales a cero se sigue que $d(x,y) \leq d(x,z)+d(z,y)$.
Por otro lado, si $x \neq y$ entonces $d(x,y) = 1$ y tenemos los siguientes casos:
Notemos que $d(x,z) = 1$ o $d(z,y) = 1$, pues de lo contrario tendríamos que $d(x,z) = 0$ y $d(z,y)=0$, lo cual implica que $x = z = y$. Por lo tanto $x = y$, lo cual es una contradicción. De lo anterior se concluye que $d(x,y)=1 \leq d(x,z) + d(z,y)$.
El conjunto de los números reales $\mathbb{R}$ con la métrica usual
Sean $x,y \in \mathbb{R}$. Entonces $d$ definida (y denotada) como
\[
d(x,y) := |x-y| := \left\{ \begin{array}{lcc}
x-y & si & x \geq y \\
\\ y-x & si & x < y
\end{array}
\right.
\]
es una métrica en $\mathbb{R}.$
Demostración:
$(1) \, $ Sean $x,y,z \in \mathbb{R}$ entonces $d(x,y)=0 \text{ si y solo si } |x-y|=0 \text{ si y solo si } x=y$.
$(2) \, $ $d(x,y)=|x-y|=|y-x|=d(y,x)$.
$(3) \, $ $d(x,y)=|x-y|=|x-z+z-y|\leq|x-z|+|z-y|=d(x,z)+d(z,y)$.
El conjunto $\mathbb R^n$ con la métrica usual
Sean $x,y,z \in \mathbb R^n$, con $x=(x_{1},…,x_{n})$, $y=(y_{1},…,y_{n})$ y $z=(z_{1},…,z_{n}),$ definimos
$$d(x,y) := \sqrt{(x_{1}-y_{1})^2+…+(x_{n}-y_{n})^2},$$
entonces $d$ es una métrica en $\mathbb{R}^n.$
Demostración:
$(1)$
\begin{align*}
d(x,y) = 0
&\iff \sqrt{(x_{1}-y_{1})^2+…+(x_{n}-y_{n})^2} = 0 \\
&\iff \forall i=1,…,n, (x_{i}-y_{i})^2 = 0 \\
&\iff\forall i=1,…,n, x_{i}=y_{i} \\
&\iff x=y
\end{align*}
$(2)$
Para cada $\, i=1,…,n, (x_{i}-y_{i})^2= (y_{i}-x_{i})^2$ entonces:
\begin{align*}
\sqrt{(x_{1}-y_{1})^2+…+(x_{n}-y_{n})^2}&=\sqrt{(y_{1}-x_{1})^2+…+(y_{n}-x_{n})^2}\\
\text{ Por lo tanto } \quad d(x,y)&=d(y,x)
\end{align*}
$(3)$
\begin{align*}
d(x,y) &= \sqrt{(x_{1}-y_{1})^2+…+(x_{n}-y_{n})^2}\\
&= \sqrt{(x_{1}-z_{1}+z_{1}-y_{1})^2+…+(x_{n}-z_{n}+z_{n}-y_{n})^2}\\
&\leq \sqrt{(x_{1}-z_{1})^2+…+(x_{n}-z_{n})^2} + \sqrt{(z_{1}-y_{1})^2+…+(z_{n}-y_{n})^2}\\
&=d(x,z)+d(z,y)
\end{align*}
Este espacio métrico es llamado el «espacio aritmético euclídeo de $n$ dimensiones $\mathbb R^n$»
El conjunto $C^0[a,b]:=\{f:[a,b] \to \mathbb R: \quad\text{f es función continua}\}$
Para recordar la definición de función continua en $\mathbb{R}$ puedes consultar el siguiente enlace: Cálculo Diferencial e Integral I: Definición de continuidad y sus propiedades.
Considera $f,g \in C^0 [a,b]$. Para cada $t \in [a,b]$ identifiquemos la medida del segmento que une a los puntos$ (t,f(t))$ y $(t,g(t))$. El segmento más grande representará la distancia entre ambas funciones.
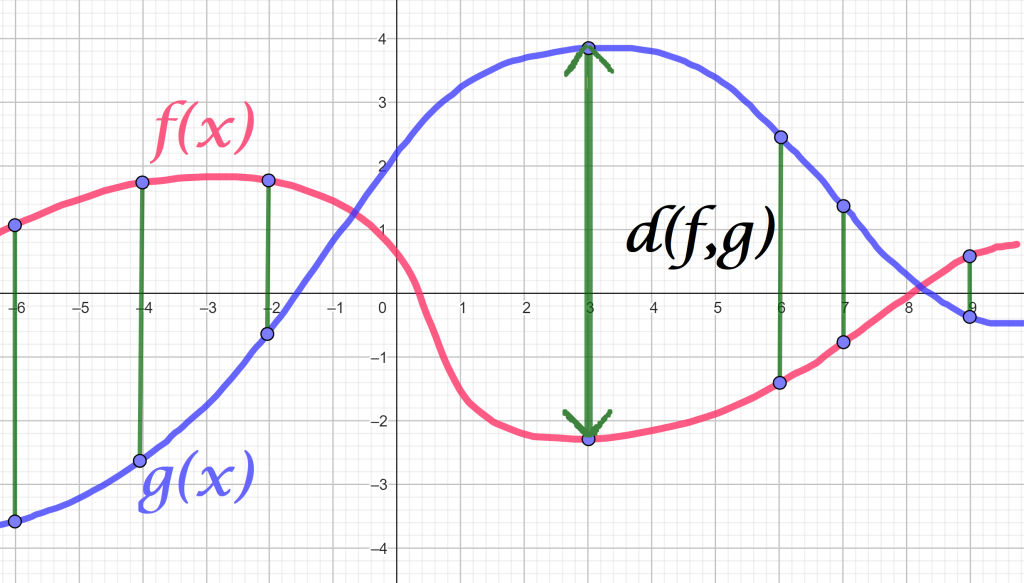
Definimos:
$$d(f,g) := \underset{a \leq t \leq b}{max}\, |f(t)-g(t)|$$
Recordemos que este máximo existe, pues al ser $f$ y $g$ funciones continuas, también lo es la función $|f-g|, \,$ (propiedad que se ve en Cálculo Diferencial e Integral I: Definición de continuidad y sus propiedades.) De acuerdo con el teorema del máximo-mínimo, (que puedes consultar en Cálculo Diferencial e Integral I: Funciones acotadas y teorema del máximo-mínimo), existe un punto en $[a,b]$ donde la función $|f-g|, \,$ alcanza su máximo. En consecuencia $d$ es una métrica en el espacio de funciones $ C^0 [a,b].$
Demostración: Sean $f, g \in C^0 [a,b]$
$(1)$ \begin{align*} d(f,g) = 0 &\iff 0 = \underset{a \leq t \leq b}{max}\, |f(t)-g(t)|\\
&\iff \forall t \in [a,b], |f(t)-g(t)| =0\\
&\iff \forall t \in [a,b], f(t) = g(t)\\
&\iff f=g
\end{align*}
$(2)$
Como $\forall t \in [a,b], f(t)$ y $g(t) \in \mathbb{R} $, entonces $|f(t)-g(t)| = |g(t)-f(t)|$. Así:
\begin{align*}
d(f,g) &= \underset{a \leq t \leq b}{max}\, |f(t)-g(t)|\\
&= \underset{a \leq t \leq b}{max}\, |g(t)-f(t)|\\
&= d(g,f)\\
\text{Por lo tanto }\quad d(f,g) &= d(g,f).
\end{align*}
$(3)$
Dado que existe $t_1 \in [a,b]$ tal que
$\underset{a \leq t \leq b}{max}\,|f(t)-g(t)| = |f(t_{1}) – g(t_{1})|$
Como
\begin{align*}|f(t_{1}) – g(t_{1})| &= |f(t_{1})-h(t_{1})+h(t_{1})-g(t_{1})|\\
&\leq |f(t_{1}) – h(t_{1})| + |h(t_{1} – g(t_{1}))|\\
& \leq \underset{a \leq t \leq b}{max}\, |f(t)-h(t)| + \underset{a \leq t \leq b}{max}\, |h(t)-g(t)|
\end{align*}
concluimos $d(f,g) \leq d(f,h) + d(h,g)$.
El conjunto $\mathcal{B}(A,\mathbb{R}):= \{ f:A \to \mathbb{R}: f\text{ es acotada}\}$
Antes de definir una métrica en el espacio anunciado, recordemos un concepto que probablemente conoces:
Definición. Función acotada. Sea $A$ un conjunto no vacío. Decimos que una función $f:A \to \mathbb{R}$ es acotada si existe $M \in \mathbb{R}$ y $x_0 \in \mathbb{R}$ tales que para cada $ \, a \in A$ ocurre que $|x_0-f(a)| \leq M$.
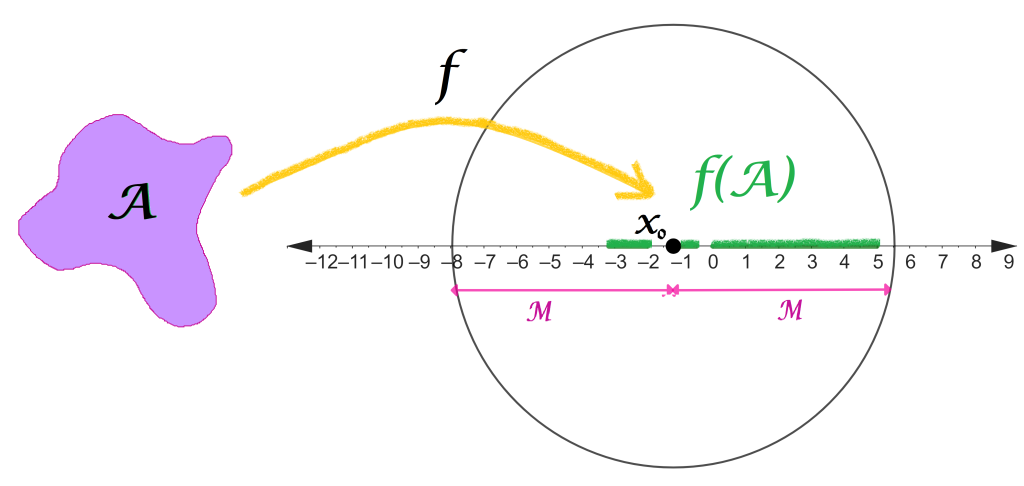
Nuestra distancia será entre funciones que satisfacen la siguiente:
Definición. Espacio de funciones acotadas. El conjunto $$\mathcal{B}(A,\mathbb{R}):= \{ f:A \to \mathbb{R}: f\text{ es acotada}\}$$ es un espacio métrico pues si dos funciones $f,g \in \mathcal{B}(A, \mathbb{R})$ entonces la función $f-g \,$ también es acotada, por lo tanto existe el $\underset{z\in A}{sup}\,|f(z)-g(z)|$. Esto permite definir la distancia entre ellas como $$d_\infty (f,g):= \underset{z\in A}{sup}\,|f(z)-g(z)|$$ y recibe el nombre de métrica uniforme.
La siguiente imagen representa la distancia entre dos funciones acotadas $f$ y $g.$ Como ejemplo, la función $f$ es la función de Dirichlet, que vale $1$ si se evalúa en los racionales ($\mathbb{Q}$) y vale $0$ en caso contrario.
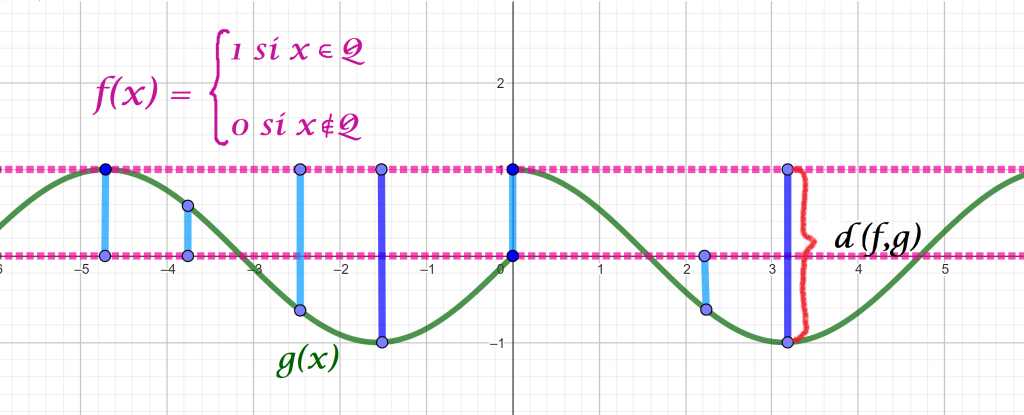
Veamos que $d_\infty$ en efecto, es métrica.
Demostración: Sean $f,g,h \in \mathcal{B}(A,\mathbb{R})$ entonces:
$(1)$ \begin{align*}
d_\infty(f,g)&=0 \\
\Leftrightarrow \underset{z\in A}{sup}\,|(f(z)-g(z)|&=0 \\
\Leftrightarrow \forall \, z \in A, |f(z)-g(z)|&=0 \\
\Leftrightarrow \forall \, z \in A, f(z)&=g(z) \\
\Leftrightarrow f&=g. \\
\text{Por lo tanto: } d_\infty (f,g)=0 &\Leftrightarrow f=g
\end{align*}
$(2)$ \begin{align*}
d_\infty (f,g)&=\underset{z\in A}{sup}\,|f(z)-g(z)|\\
&=\underset{z\in A}{sup}\,|g(z)-f(z)| \\
&=d_\infty(g,f).\\
\text{Por lo tanto: } d_\infty(f,g)&=d_\infty(g,f)
\end{align*}
$(3)$ \begin{align*}
d_\infty(f,g)&=\underset{z\in A}{sup}\,|f(z)-g(z)|\\
&\leq \underset{z\in A}{sup}\,\{|f(z)-h(z)|+|h(z)-g(z)|\}\\
&\leq \underset{z\in A}{sup}\,|f(z)-h(z)| + \underset{z\in A}{sup}\,|h(z)-g(z)|\\
&\leq d_\infty(f,h)+d_\infty(h,g)\\
\text{Por lo tanto: }d_\infty(f,g)&\leq d_\infty(f,h)+d_\infty(h,g)
\end{align*}
Más adelante…
Ya aprendimos qué es un espacio métrico y comprobamos que las distancias vistas en otros cursos satisfacen la definición. En la siguiente entrada conoceremos algunos ejemplos más con la finalidad de hacer consciente que hay otras maneras de medir la separación entre dos objetos.
Tarea moral
¡Es tu turno de practicar!
- Sean $x,y \in \mathbb R^2$ con $x=(x_{1},x_{2})$ y $y=(y_{1},y_{2}).$ Demuestra que $d(x,y) := \sqrt{(x_{1}-y_{1})^2 + 4(x_{2}-y_{2})^2}$ es métrica para $\mathbb{R}^2.$
- Sean $x,y \in \mathbb R^n$ con $x=(x_{1},…,x_{n})$ y $y=(y_{1},…,y_{n}).$ Demuestra que $d(x,y) := |x_{1}-y_{1}|+…+|x_{n}-y_{n}|$ es métrica para $\mathbb{R}^n.$
- Sean $x,y \in \mathbb R^n$ con $x=(x_{1},…,x_{n})$ y $y=(y_{1},…,y_{n}).$ Demuestra que $d(x,y) := max \{|x_{1}-y_{1}|,…,|x_{n}-y_{n}|\}$ es métrica para $\mathbb{R}^n.$
Bibliografía
- Apostol, T., Análisis Matemático (2a ed.). México: Editorial Reverté, 1996. Págs 73,74.
- Clapp, M., Análisis Matemático. Ciudad de México: Editorial Papirhos, IM-UNAM, 2013. Págs 7-9.
- Díaz, J. M., Introducción a la topología de los espacios métricos. Cádiz: Universidad de Cádiz, Servicio de Publicaciones, 1998. Pág. i.
- Kolmogorov, A.N., Fomin, S.V., Elementos de la Teoría de Funciones y del Análisis Funcional. (2a ed.). Moscú: Editorial MIR, 1975. Pág 51-53.
Enlaces
- Análisis Matemático.
- Enlace a entrada anterior.
- Enlace a entrada siguiente.

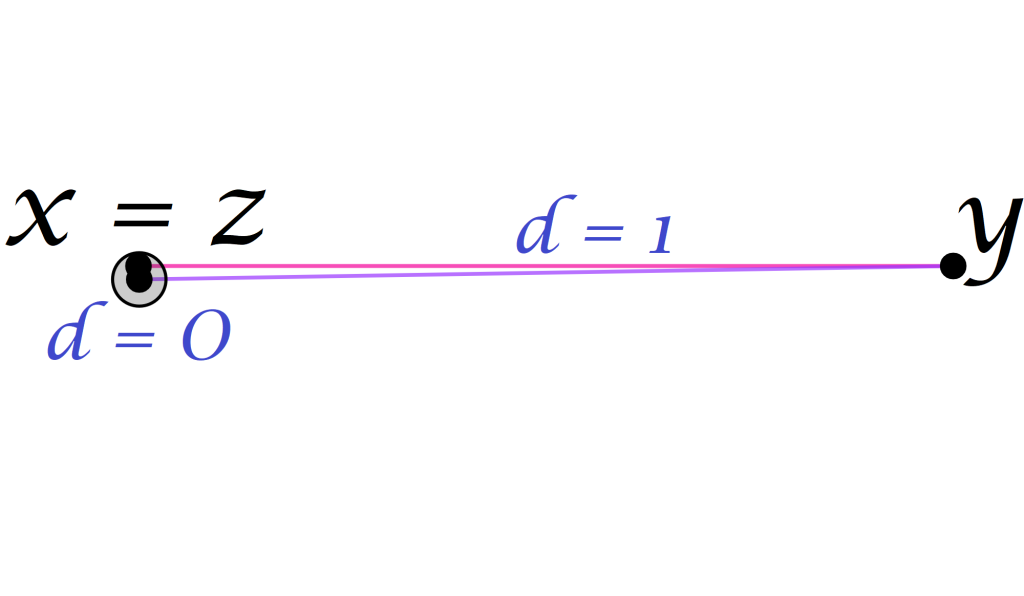
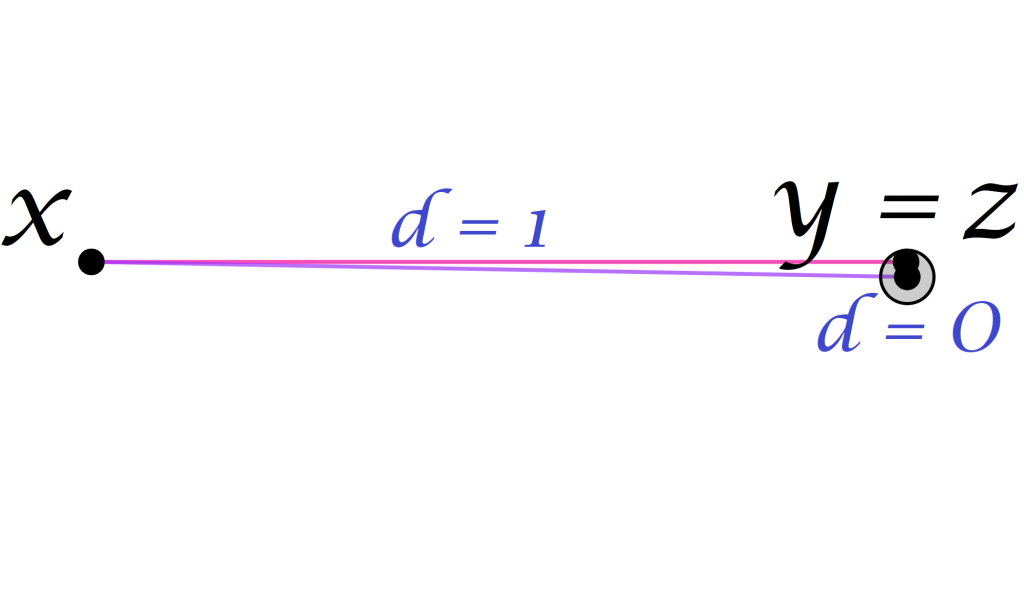
En la tarea moral inciso 3) falta ponerle los corchetes a la métrica para indicar de qué conjunto será el máximo
Gracias por la observación.
awesome