Las matemáticas es una ciencia que dibuja conclusiones necesarias.
– Benjamin Peirce

Introducción

En la entrada anterior estudiamos los sistemas lineales en los que los valores propios de la matriz $\mathbf{A}$ eran reales y distintos, en esta entrada estudiaremos sistemas lineales en los que los valores propios son complejos.

Antes de comenzar con el desarrollo cualitativo es conveniente recordar algunos resultados importantes de estos sistemas.

Sistemas lineales con valores propios complejos

El sistema que estamos analizando es

$$\begin{array}{rl}{x}^{\prime }& =ax+by\\ \text{(1)}& y^{\prime }& =cx+dy\end{array}$$

Definimos,

$${\mathbf{Y}}^{\prime }=\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right),\mathbf{Y}=\left(\begin{array}{c}x\\ y\end{array}\right)y\mathbf{A}=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$$

De manera que el sistema ($\text{1}$) se pueda escribir como

$$\begin{array}{}\text{(2)}& {\mathbf{Y}}^{\prime }=\mathbf{AY}\end{array}$$

Sea

$$\begin{array}{}\text{(3)}& \lambda =\alpha +i\beta \end{array}$$

un valor propio de la matriz $\mathbf{A}$, con $\alpha$ y $\beta$ reales. Y sea

$$\begin{array}{}\text{(4)}& \mathbf{K}=\mathbf{U}+i\mathbf{V}\end{array}$$

un vector propio de $\mathbf{A}$ asociado a $\lambda$. Entonces la solución del sistema ($\text{1}$) se puede escribir como

$$\begin{array}{}\text{(5)}& \mathbf{Y}(t)=(\mathbf{U}+i\mathbf{V})e^{(\alpha +i\beta )t}\end{array}$$

En la unidad anterior vimos que si definimos los vectores

$${\mathbf{W}}_1=Re\{\mathbf{Y}\}y{\mathbf{W}}_2=Im\{\mathbf{Y}\}$$

donde ${\mathbf{W}}_1$ y ${\mathbf{W}}_2$ están dados como

$$\begin{array}{}\text{(6)}& {\mathbf{W}}_1(t)=e^{\alpha t}[\mathbf{U}\cos (\beta t)-\mathbf{V}\sin (\beta t)]\end{array}$$

y

$$\begin{array}{}\text{(7)}& {\mathbf{W}}_2(t)=e^{\alpha t}[\mathbf{U}\sin (\beta t)+\mathbf{V}\cos (\beta t)]\end{array}$$

entonces la solución general real del sistema ($\text{1}$) es

$$\begin{array}{}\text{(8)}& \mathbf{Y}(t)=c_1{\mathbf{W}}_1(t)+c_2{\mathbf{W}}_2(t)\end{array}$$

Por lo tanto, las soluciones linealmente independientes son

$$\begin{array}{}\text{(9)}& {\mathbf{Y}}_1(t)=c_1{e}^{\alpha t}[\mathbf{U}\cos (\beta t)-\mathbf{V}\sin (\beta t)]\end{array}$$

y

$$\begin{array}{}\text{(10)}& {\mathbf{Y}}_2(t)=c_2{e}^{\alpha t}[\mathbf{U}\sin (\beta t)+\mathbf{V}\cos (\beta t)]\end{array}$$

La expresión $k_1\cos (\beta t)+k_2\sin (\beta t)$, donde $k_1$ y $k_2$ son constantes, se puede expresar en la forma $R\cos (\beta t-\delta )$ para una elección adecuada de constantes $R$ y $\delta$. De tarea moral demuestra que la solución ($\text{8}$) se puede expresar de la siguiente forma.

$$\begin{array}{}\text{(11)}& \mathbf{Y}(t)=e^{\alpha t}\left(\begin{array}{c}{R}_1\cos (\beta t-{\delta }_1)\\ R_2\cos (\beta t-{\delta }_2)\end{array}\right)\end{array}$$

para alguna elección de constantes $R_1\ge 0$, $R_2\ge 0$, ${\delta }_1$ y ${\delta }_2$.

Con esto en mente pasemos a estudiar cada caso en el que los valores propios son complejos.

Valores propios complejos con parte real nula

Caso 1: ${\lambda }_1=\alpha +i\beta$ y ${\lambda }_2=\alpha -i\beta$, con $\alpha =0$.

En este caso se dice que los valores propios son imaginarios puros ya que no tienen parte real. De la solución ($\text{11}$) vemos que si $\alpha =0$, entonces la expresión se reduce a

$$\begin{array}{}\text{(12)}& \mathbf{Y}(t)=\left(\begin{array}{c}{R}_1\cos (\beta t-{\delta }_1)\\ R_2\cos (\beta t-{\delta }_2)\end{array}\right)\end{array}$$

Las soluciones $x(t)$ y $y(t)$ son

$$\begin{array}{}\text{(13)}& x(t)=R_1\cos (\beta t-{\delta }_1)yy(t)=R_2\cos (\beta t-{\delta }_2)\end{array}$$

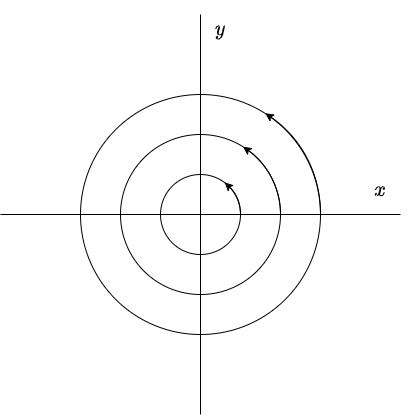
Estas funciones son periódicas en el tiempo, con periodo $2\pi /\beta$. Como $|\cos (\beta t-{\delta }_1)|\le 1$ y $|\cos (\beta t-{\delta }_2)|\le 1$, entonces la función $x(t)$ varia entre $-R_1$ y $+R_1$, mientras que $y(t)$ varia entre $-R_2$ y $+R_2$. Por tanto, la trayectoria de cualquier solución $\mathbf{Y}(t)$ de ($\text{1}$) es una curva cerrada que rodea al origen $x=y=0$, es por ello que se dice que el punto de equilibrio $Y_0=(0,0)$ es un centro y es estable.

A continuación se muestra el plano fase.

La dirección de las trayectorias se determina a partir del sistema ($\text{1}$). Buscamos el signo de $y^{\prime }$ cuando $y=0$. Si $y^{\prime }$ es mayor que cero para $y=0$ y $x>0$, entonces todas las trayectorias se mueven en sentido contrario a las manecillas del reloj. Si $y^{\prime }$ es menor que cero para $y=0$ y $x>0$, entonces todas las trayectorias se mueven en el sentido de las manecillas del reloj.

Ahora estudiemos los casos en los que los valores propios tienen parte real no nula.

Valores propios complejos con parte real negativa

Caso 2: ${\lambda }_1=\alpha +i\beta$ y ${\lambda }_2=\alpha -i\beta$, con $\alpha <0$.

En este caso las soluciones son

$$\mathbf{Y}(t)=e^{\alpha t}\left(\begin{array}{c}{R}_1\cos (\beta t-{\delta }_1)\\ R_2\cos (\beta t-{\delta }_2)\end{array}\right)$$

o bien,

$$\begin{array}{}\text{(14)}& x(t)=e^{\alpha t}{R}_1\cos (\beta t-{\delta }_1)yy(t)=e^{\alpha t}{R}_2\cos (\beta t-{\delta }_2)\end{array}$$

Si $t=0$, se obtiene que

$$\begin{array}{}\text{(15)}& \mathbf{Y}(0)=\left(\begin{array}{c}{R}_1\cos (-{\delta }_1)\\ R_2\cos (-{\delta }_2)\end{array}\right)\end{array}$$

Sabemos que el periodo es $2\pi /\beta$, notemos que si $t=2\pi /\beta$, entonces

$$\mathbf{Y}(2\pi /\beta )=e^{2\pi \alpha /\beta }\left(\begin{array}{c}{R}_1\cos (2\pi -{\delta }_1)\\ R_2\cos (2\pi -{\delta }_2)\end{array}\right)=e^{2\pi \alpha /\beta }\left(\begin{array}{c}{R}_1\cos (-{\delta }_1)\\ R_2\cos (-{\delta }_2)\end{array}\right)$$

esto es,

$$\begin{array}{}\text{(16)}& \mathbf{Y}(2\pi /\beta )=e^{2\pi \alpha /\beta }\mathbf{Y}(0)\end{array}$$

Como

$$\mathbf{Y}(2\pi /\beta )<\mathbf{Y}(0)$$

es decir,

$$x(2\pi /\beta )<x(0)yy(2\pi /\beta )<y(0)$$

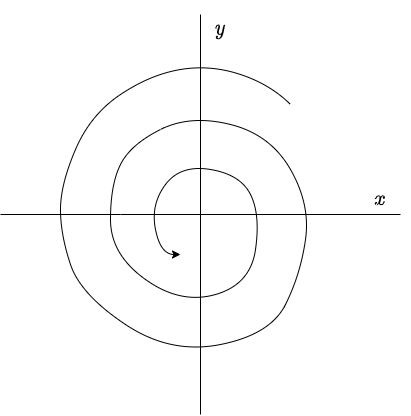
entonces $\mathbf{Y}(2\pi /\beta )$ está más cerca del origen que $\mathbf{Y}(0)$. Esto significa que, para $\alpha <0$, el efecto del factor $e^{\alpha t}$ sobre la solución ($\text{11}$) es el de cambiar las curvas cerradas del caso anterior en espirales que se aproximan hacia el origen.

El plano fase se muestra a continuación.

De forma similar al caso anterior, la dirección de las trayectorias se determina a partir del sistema ($\text{1}$). En este caso se dice que el punto de equilibrio $Y_0=(0,0)$ de ($\text{1}$) es un foco estable, o también se conoce como espiral atractor. La estabilidad de este punto de equilibrio es asintóticamente estable.

Para concluir veamos que ocurre si $\alpha$ es positiva.

Valores propios complejos con parte real positiva

Caso 3: ${\lambda }_1=\alpha +i\beta$ y ${\lambda }_2=\alpha -i\beta$, con $\alpha >0$.

En este caso nuevamente las soluciones son

$$\mathbf{Y}(t)=e^{\alpha t}\left(\begin{array}{c}{R}_1\cos (\beta t-{\delta }_1)\\ R_2\cos (\beta t-{\delta }_2)\end{array}\right)$$

o bien,

$$x(t)=e^{\alpha t}{R}_1\cos (\beta t-{\delta }_1)yy(t)=e^{\alpha t}{R}_2\cos (\beta t-{\delta }_2)$$

Sin embargo, debido a que $\alpha >0$, se puede probar que

$$\mathbf{Y}(2\pi /\beta )>\mathbf{Y}(0)$$

es decir,

$$x(2\pi /\beta )>x(0)yy(2\pi /\beta )>y(0)$$

lo que significa que ahora $\mathbf{Y}(0)$ está más cerca del origen que $\mathbf{Y}(2\pi /\beta )$.

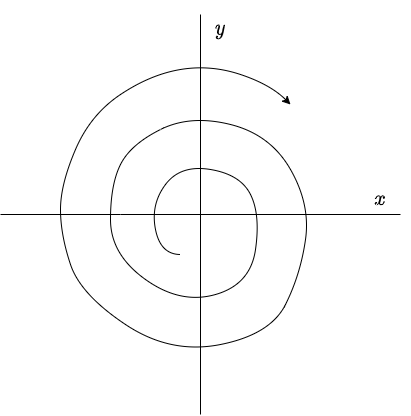
Por lo tanto, en este caso todas las soluciones de ($\text{1}$) describen espirales que se alejan del origen conforme $t\to \mathrm{\infty }$, y se dice que el punto de equilibrio $Y_0=(0,0)$ de ($\text{1}$) es un foco inestable o espiral repulsor. Es claro que el punto de equilibrio es inestable.

El plano fase se muestra a continuación.

Hemos revisado los casos posibles. Para concluir con la entrada realicemos un ejemplo por cada caso.

Caso 1: ${\lambda }_1=\alpha +i\beta$ y ${\lambda }_2=\alpha -i\beta$, con $\alpha =0$.

Ejemplo: Resolver el siguiente sistema lineal y hacer un análisis cualitativo de las soluciones.

$${\mathbf{Y}}^{\prime }=\left(\begin{array}{cc}2& 1\\ -5& -2\end{array}\right)\mathbf{Y}$$

Solución: Determinemos los valores propios.

$$\left|\begin{array}{cc}2-\lambda & 1\\ -5& -2-\lambda \end{array}\right|=(2-\lambda )(-2-\lambda )+5={\lambda }^2+1=0$$

Las raíces son ${\lambda }_1=i$ y ${\lambda }_2=-i$, notamos que $\alpha =0$ y $\beta =1$, determinemos los vectores propios resolviendo la ecuación

$$(\mathbf{A}-i\mathbf{I})\mathbf{K}=\mathbf{0}$$

o bien,

$$\left(\begin{array}{cc}2-i& 1\\ -5& -2-i\end{array}\right)\left(\begin{array}{c}{k}_1\\ k_2\end{array}\right)=\left(\begin{array}{c}0\\ 0\end{array}\right)$$

Las ecuaciones que se obtienen son

$$\begin{array}{rl}(2-i)k_1+k_2& =0\\ -5k_1-(2+i)k_2& =0\end{array}$$

Vemos que

$$k_1=-\left({\displaystyle \frac{2+i}{5}}\right)k_2$$

Sea $k_2=-5$, tal que $k_1=2+i$, así el primer vector propio es

$${\mathbf{K}}_1=\left(\begin{array}{c}2+i\\ -5\end{array}\right)=\left(\begin{array}{c}2\\ -5\end{array}\right)+i\left(\begin{array}{c}1\\ 0\end{array}\right)$$

Sabemos que ${\mathbf{K}}_2={\overline{\mathbf{K}}}_1$, entonces el segundo vector propio asociado al valor propio ${\lambda }_2=-i$ es

$${\mathbf{K}}_2=\left(\begin{array}{c}2-i\\ -5\end{array}\right)=\left(\begin{array}{c}2\\ -5\end{array}\right)-i\left(\begin{array}{c}1\\ 0\end{array}\right)$$

La primera solución linealmente independiente es

$${\mathbf{Y}}_1(t)=e^{it}\left(\begin{array}{c}2+i\\ -5\end{array}\right)$$

Notemos lo siguiente.

$$\begin{array}{rl}{e}^{it}\left(\begin{array}{c}2+i\\ -5\end{array}\right)& =[\cos (t)+i\sin (t)][\left(\begin{array}{c}2\\ -5\end{array}\right)+i\left(\begin{array}{c}1\\ 0\end{array}\right)]\\ & =\cos (t)\left(\begin{array}{c}2\\ -5\end{array}\right)-\sin (t)\left(\begin{array}{c}1\\ 0\end{array}\right)+i\cos (t)\left(\begin{array}{c}1\\ 0\end{array}\right)+i\sin (t)\left(\begin{array}{c}2\\ -5\end{array}\right)\end{array}$$

De donde definimos

$${\mathbf{W}}_1=\cos (t)\left(\begin{array}{c}2\\ -5\end{array}\right)-\sin (t)\left(\begin{array}{c}1\\ 0\end{array}\right)$$

y

$${\mathbf{W}}_2=\sin (t)\left(\begin{array}{c}2\\ -5\end{array}\right)+\cos (t)\left(\begin{array}{c}1\\ 0\end{array}\right)$$

Por lo tanto, la solución general real es

$$\mathbf{Y}(t)=c_1[\cos (t)\left(\begin{array}{c}2\\ -5\end{array}\right)-\sin (t)\left(\begin{array}{c}1\\ 0\end{array}\right)]+c_2[\sin (t)\left(\begin{array}{c}2\\ -5\end{array}\right)+\cos (t)\left(\begin{array}{c}1\\ 0\end{array}\right)]$$

En términos de las funciones $x(t)$ y $y(t)$ se tienen las soluciones

$$\begin{array}{rl}x(t)& =[2c_1+c_2]\cos (t)+[-c_1+2c_2]\sin (t)\\ y(t)& =-5c_1\cos (t)-5c_2\sin (t)\end{array}$$

Las soluciones son de la forma

$$\begin{array}{rl}x(t)& =k_1\cos (t)+k_2\sin (t)\\ y(t)& =k_3\cos (t)+k_4\sin (t)\end{array}$$

También es posible determinar las constantes $R_1$, $R_2$, ${\delta }_1$ y ${\delta }_2$ en términos de las constantes $c_1$ y $c_2$, tal que la solución se pueda escribir como

$$\begin{array}{rl}x(t)& =R_1\cos (t-{\delta }_1)\\ y(t)& =R_2\cos (t-{\delta }_2)\end{array}$$

En este caso como $\beta =1$, entonces el periodo es $T=2\pi$. La función paramétrica que define las trayectorias está dada por

$$f(t)=(k_1\cos (t)+k_2\sin (t),k_3\cos (t)+k_4\sin (t))$$

Es claro que las trayectorias son curvas cerradas con periodo $2\pi$.

Para determinar la dirección de las trayectorias consideremos la ecuación $y^{\prime }$ del sistema, dicha ecuación es

$$y^{\prime }=-5x-2y$$

Si $y=0$ se tiene la ecuación $y^{\prime }=-5x$, vemos que si $x>0$, entonces $y^{\prime }<0$, por lo tanto las trayectorias se mueven en el sentido de las manecillas del reloj.

El plano fase indicando algunas trayectorias se muestra a continuación.

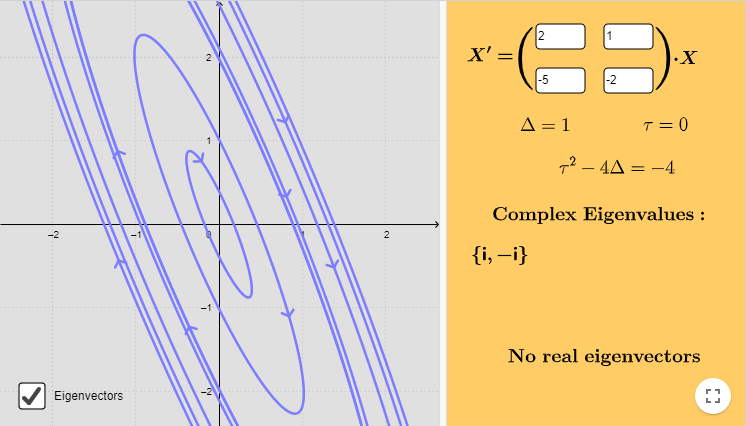
El campo vectorial está definido por la función

$$F(x,y)=(2x+y,-5x-2y)$$

A continuación se muestra dicho campo vectorial y algunas trayectorias.

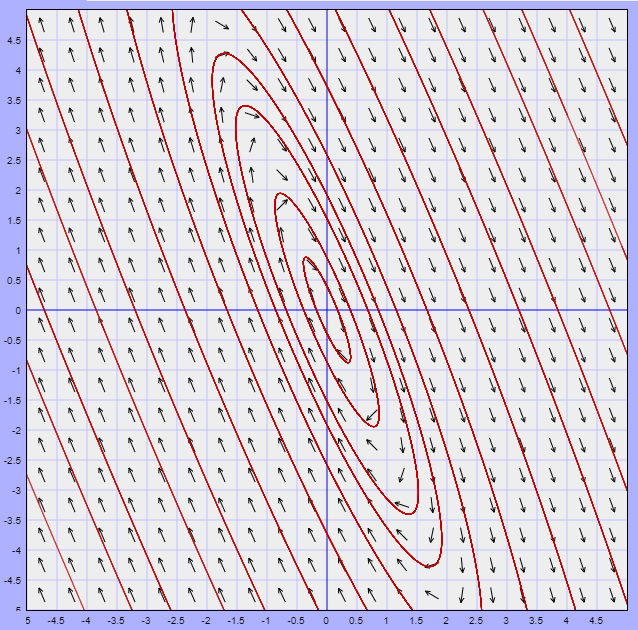
Efectivamente, el punto de equilibrio $Y_0=(0,0)$ es un centro.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Veamos como se pierde esta regularidad si $\alpha \ne 0$.

Caso 2: ${\lambda }_1=\alpha +i\beta$ y ${\lambda }_2=\alpha -i\beta$, con $\alpha <0$.

Ejemplo: Resolver el siguiente sistema lineal y hacer un análisis cualitativo de las soluciones.

$${\mathbf{Y}}^{\prime }=\left(\begin{array}{cc}-1& -4\\ 1& -1\end{array}\right)\mathbf{Y}$$

Solución: Determinemos los valores propios.

$$\left|\begin{array}{cc}-1-\lambda & -4\\ 1& -1-\lambda \end{array}\right|=(-1-\lambda {)}^2+4={\lambda }^2+2\lambda +5=0$$

Las raíces son ${\lambda }_1=-1+2i$ y ${\lambda }_2=-1-2i$ (con $\alpha =-1$ y $\beta =2$). Resolvamos la siguiente ecuación para obtener los vectores propios.

$$(\mathbf{A}-(-1+2i)\mathbf{I})\mathbf{K}=\mathbf{0}$$

o bien,

$$\left(\begin{array}{cc}-2i& -4\\ 1& -2i\end{array}\right)\left(\begin{array}{c}{k}_1\\ k_2\end{array}\right)=\left(\begin{array}{c}0\\ 0\end{array}\right)$$

Se obtiene que $k_1=2i{k}_2$. Sea $k_2=1$, entonces $k_1=2i$, así el primer vector propios es

$${\mathbf{K}}_1=\left(\begin{array}{c}2i\\ 1\end{array}\right)=\left(\begin{array}{c}0\\ 1\end{array}\right)+i\left(\begin{array}{c}2\\ 0\end{array}\right)$$

Considerando que ${\mathbf{K}}_2={\overline{\mathbf{K}}}_1$ , entonces el segundo vector propio, asociado a ${\lambda }_2=-1-2i$ es

$${\mathbf{K}}_2=\left(\begin{array}{c}-2i\\ 1\end{array}\right)=\left(\begin{array}{c}0\\ 1\end{array}\right)-i\left(\begin{array}{c}2\\ 0\end{array}\right)$$

Sabemos que la primer solución es

$${\mathbf{Y}}_1(t)=e^{(-1+2i)t}\left(\begin{array}{c}2i\\ 1\end{array}\right)$$

Notemos lo siguiente.

$$\begin{array}{rl}{e}^{(-1+2i)t}\left(\begin{array}{c}2i\\ 1\end{array}\right)& =e^{-t}[\cos (2t)+i\sin (2t)][\left(\begin{array}{c}0\\ 1\end{array}\right)+i\left(\begin{array}{c}2\\ 0\end{array}\right)]\\ & =e^{-t}[\cos (2t)\left(\begin{array}{c}0\\ 1\end{array}\right)-\sin (2t)\left(\begin{array}{c}2\\ 0\end{array}\right)+i\cos (2t)\left(\begin{array}{c}2\\ 0\end{array}\right)+i\sin (2t)\left(\begin{array}{c}0\\ 1\end{array}\right)]\end{array}$$

De donde definimos

$${\mathbf{W}}_1(t)=e^{-t}[\cos (2t)\left(\begin{array}{c}0\\ 1\end{array}\right)-\sin (t)\left(\begin{array}{c}2\\ 0\end{array}\right)]$$

y

$${\mathbf{W}}_2(t)=e^{-t}[\cos (t)\left(\begin{array}{c}2\\ 0\end{array}\right)+\sin (2t)\left(\begin{array}{c}0\\ 1\end{array}\right)]$$

Por lo tanto, la solución general real es

$$\mathbf{Y}(t)=c_1{e}^{-t}[\cos (2t)\left(\begin{array}{c}0\\ 1\end{array}\right)-\sin (t)\left(\begin{array}{c}2\\ 0\end{array}\right)]+c_2{e}^{-t}[\cos (t)\left(\begin{array}{c}2\\ 0\end{array}\right)+\sin (2t)\left(\begin{array}{c}0\\ 1\end{array}\right)]$$

Las funciones $x(t)$ y $y(t)$ son

$$\begin{array}{rl}x(t)& =-2c_1{e}^{-t}\sin (2t)+2c_2{e}^{-t}\cos (2t)\\ y(t)& =c_1{e}^{-t}\cos (2t)+c_2{e}^{-t}\sin (2t)\end{array}$$

Estas funciones también se pueden escribir como

$$\begin{array}{rl}x(t)& =e^{-t}{R}_1\cos (2t-{\delta }_1)\\ y(t)& =e^{-t}{R}_2\cos (2t-{\delta }_2)\end{array}$$

De tarea moral determina las constantes $R_1$, $R_2$, ${\delta }_1$ y ${\delta }_2$ en términos de las constantes $c_1$ y $c_2$.

Podemos notar que las soluciones ya no son trayectorias cerradas debido al término $e^{-t}$. En este caso el periodo es $t=2\pi /2=\pi$. Notemos que

$$\begin{array}{rl}x(0)& =2c_2=R_1\cos (-{\delta }_1)\\ y(0)& =c_1=R_2\cos (-{\delta }_2)\end{array}$$

Mientras que

$$\begin{array}{rl}x(\pi )& =2e^{-\pi }{c}_2=R_1{e}^{-\pi }\cos (-{\delta }_1)\\ y(\pi )& =e^{-\pi }{c}_1=R_2{e}^{-\pi }\cos (-{\delta }_2)\end{array}$$

Como $e^{-\pi }<1$, entonces

$$x(\pi )<x(0)yy(\pi )<y(0)$$

Por lo tanto las trayectorias corresponden a espirales que se aproximan hacia el origen.

La función paramétrica que define las trayectorias es

$$f(t)=(-2c_1{e}^{-t}\sin (2t)+2c_2{e}^{-t}\cos (2t),c_1{e}^{-t}\cos (2t)+c_2{e}^{-t}\sin (2t))$$

Para determinar la dirección en que giran las trayectorias consideremos la ecuación $y^{\prime }$ del sistema, dicha ecuación es

$$y^{\prime }=x-y$$

Si $y=0$, entonces $y^{\prime }=x$ y si $x>0$, entonces $y^{\prime }>0$, por lo tanto las trayectorias se mueven en el sentido opuesto a las manecillas del reloj.

El plano fase con algunas trayectorias se muestra a continuación.

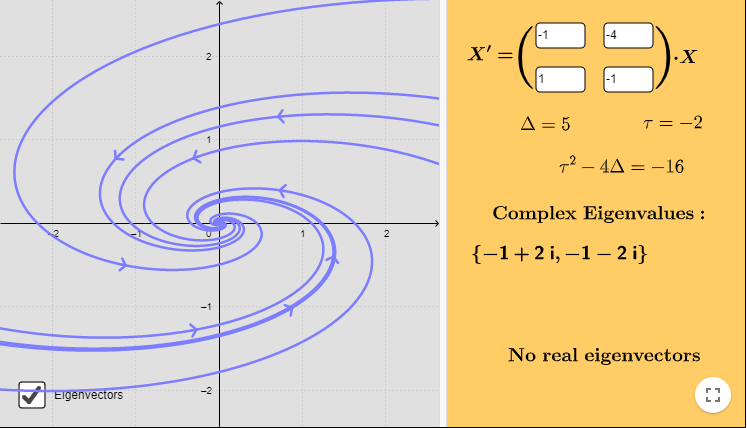
El campo vectorial asociado está definido por la función

$$F(x,y)=(-x-4y,x-y)$$

Dicho campo y algunas trayectorias se muestran en la siguiente figura.

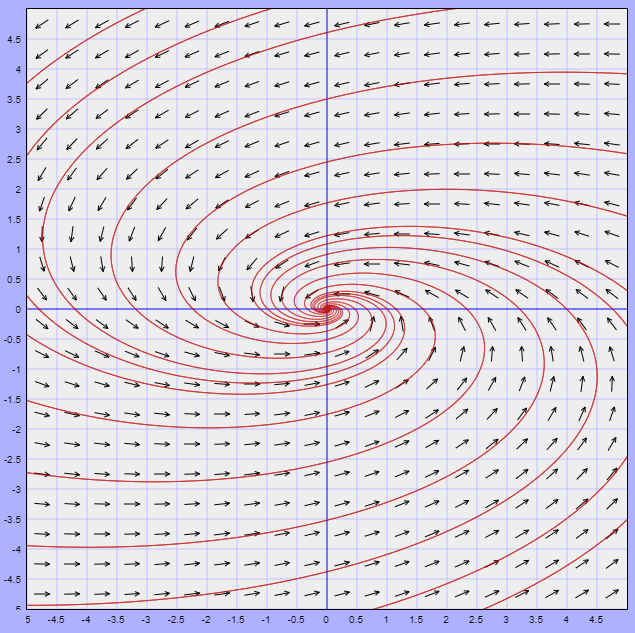
El punto de equilibrio $Y_0=(0,0)$ es un foco estable.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Concluyamos con un último ejemplo.

Caso 3: ${\lambda }_1=\alpha +i\beta$ y ${\lambda }_2=\alpha -i\beta$, con $\alpha >0$.

Ejemplo: Resolver el siguiente sistema lineal y hacer un análisis cualitativo de las soluciones.

$${\mathbf{Y}}^{\prime }=\left(\begin{array}{cc}3& -2\\ 4& -1\end{array}\right)\mathbf{Y}$$

Solución: Determinemos los valores propios.

$$\left|\begin{array}{cc}3-\lambda & -2\\ 4& -1-\lambda \end{array}\right|=(3-\lambda )(-1-\lambda )+8={\lambda }^2-2\lambda +5=0$$

Los valores propios son ${\lambda }_1=1+2i$ y ${\lambda }_2=1-2i$ (con $\alpha =1$ y $\beta =2$ ). Determinemos los vectores propios con la ecuación

$$(\mathbf{A}-(1+2i)\mathbf{I})\mathbf{K}=\mathbf{0}$$

o bien,

$$\left(\begin{array}{cc}2-2i& -2\\ 4& -2-2i\end{array}\right)\left(\begin{array}{c}{k}_1\\ k_2\end{array}\right)=\left(\begin{array}{c}0\\ 0\end{array}\right)$$

De este sistema se obtiene que

$$k_1=\left({\displaystyle \frac{1+i}{2}}\right)k_2$$

Sea $k_2=1$, entonces $k_1={\displaystyle \frac{1+i}{2}}$, así el primer vector propio es

$${\mathbf{K}}_1=\left(\begin{array}{c}{\displaystyle \frac{1+i}{2}}\\ 1\end{array}\right)=\left(\begin{array}{c}0\\ 1\end{array}\right)+i\left(\begin{array}{c}{\displaystyle \frac{1}{2}}\\ 0\end{array}\right)$$

y sabemos enseguida que

$${\mathbf{K}}_2=\left(\begin{array}{c}{\displaystyle \frac{1-i}{2}}\\ 1\end{array}\right)=\left(\begin{array}{c}0\\ 1\end{array}\right)-i\left(\begin{array}{c}{\displaystyle \frac{1}{2}}\\ 0\end{array}\right)$$

La primer solución linealmente independiente es

$$Y_1(t)=e^{(1+2i)t}\left(\begin{array}{c}{\displaystyle \frac{1+i}{2}}\\ 1\end{array}\right)$$

Vemos que

$$\begin{array}{rl}{e}^{(1+2i)t}\left(\begin{array}{c}{\displaystyle \frac{1+i}{2}}\\ 1\end{array}\right)& =e^t[\cos (2t)+i\sin (2t)][\left(\begin{array}{c}{\displaystyle \frac{1}{2}}\\ 1\end{array}\right)+i\left(\begin{array}{c}{\displaystyle \frac{1}{2}}\\ 0\end{array}\right)]\\ & =e^t[\cos (2t)\left(\begin{array}{c}{\displaystyle \frac{1}{2}}\\ 1\end{array}\right)-\sin (2t)\left(\begin{array}{c}{\displaystyle \frac{1}{2}}\\ 0\end{array}\right)+i\cos (2t)\left(\begin{array}{c}{\displaystyle \frac{1}{2}}\\ 0\end{array}\right)+i\sin (2t)\left(\begin{array}{c}{\displaystyle \frac{1}{2}}\\ 1\end{array}\right)]\end{array}$$

de donde,

$${\mathbf{W}}_1(t)=e^t[\cos (2t)\left(\begin{array}{c}{\displaystyle \frac{1}{2}}\\ 1\end{array}\right)-\sin (2t)\left(\begin{array}{c}{\displaystyle \frac{1}{2}}\\ 0\end{array}\right)]$$

y

$${\mathbf{W}}_2(t)=e^t[\cos (2t)\left(\begin{array}{c}{\displaystyle \frac{1}{2}}\\ 0\end{array}\right)+\sin (2t)\left(\begin{array}{c}{\displaystyle \frac{1}{2}}\\ 1\end{array}\right)]$$

Por lo tanto, la solución general real del sistema es

$$\mathbf{Y}(t)=c_1{e}^t[\cos (2t)\left(\begin{array}{c}{\displaystyle \frac{1}{2}}\\ 1\end{array}\right)-\sin (2t)\left(\begin{array}{c}{\displaystyle \frac{1}{2}}\\ 0\end{array}\right)]+c_2{e}^t[\cos (2t)\left(\begin{array}{c}{\displaystyle \frac{1}{2}}\\ 0\end{array}\right)+\sin (2t)\left(\begin{array}{c}{\displaystyle \frac{1}{2}}\\ 1\end{array}\right)]$$

Las funciones $x(t)$ y $y(t)$ son

$$\begin{array}{rl}x(t)& =e^t\left({\displaystyle \frac{c_1+c_2}{2}}\right)\cos (2t)+e^t\left({\displaystyle \frac{c_2-c_1}{2}}\right)\sin (2t)\\ y(t)& =c_1{e}^t\cos (2t)+c_2{e}^t\sin (2t)\end{array}$$

El periodo de las soluciones es $T=2\pi /2=\pi$. Muestra, de manera similar a como lo hicimos en el ejemplo anterior, que

$$x(\pi )>x(0)yy(\pi )>y(0)$$

esto debido a que $e^{\pi }>1$. Por lo tanto, las trayectorias describen espirales que se alejan del origen.

La función paramétrica que define a las trayectorias es

$$f(t)=(k_1{e}^t\cos (2t)+k_2{e}^t\sin (2t),c_1{e}^t\cos (2t)+c_2{e}^t\sin (2t))$$

Con

$$k_1=\left({\displaystyle \frac{c_1+c_2}{2}}\right)y{k}_2=\left({\displaystyle \frac{c_2-c_1}{2}}\right)$$

Para determinar la dirección de las trayectorias consideremos la ecuación

$$y^{\prime }=4x-y$$

Si $y=0$ se obtiene que $y^{\prime }=4x$ y si $x>0$, entonces $y^{\prime }>0$, por lo tanto, las trayectorias se mueven en el sentido opuesto a las manecillas del reloj.

El plano fase se muestra a continuación.

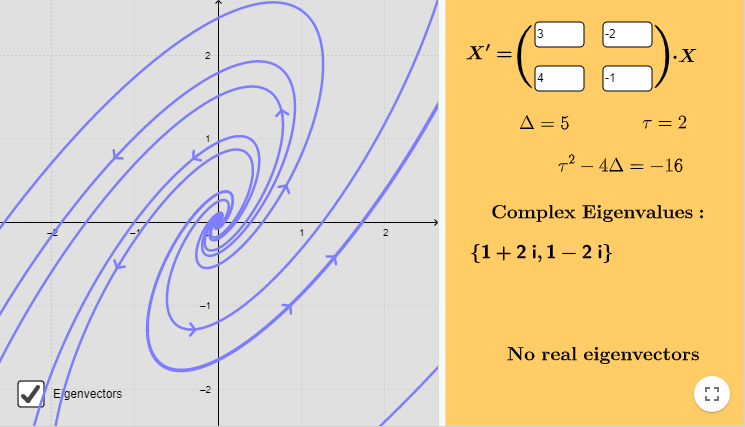
La función vectorial que define al campo vectorial es

$$F(x,y)=(3x-2y,4x-y)$$

El campo vectorial y algunas trayectorias se ilustran en la siguiente figura.

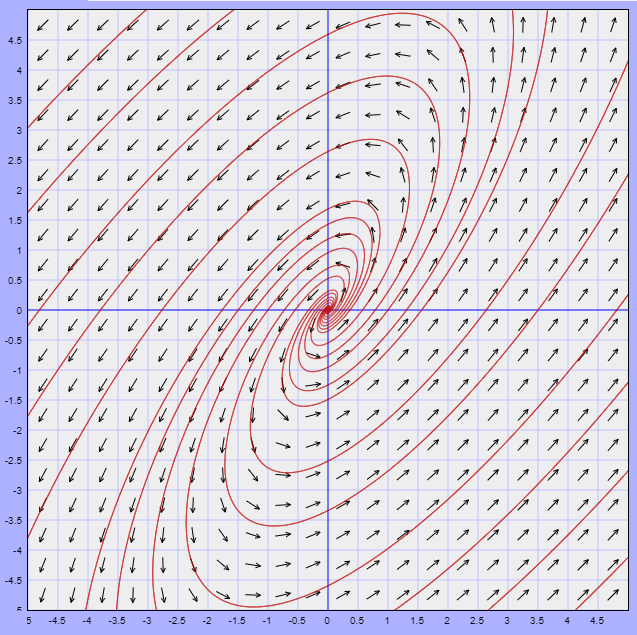
El punto de equilibrio $Y_0=(0,0)$ corresponde a un foco inestable.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Hemos concluido con esta entrada. Continuemos en la siguiente entrada con el análisis en el caso en el que los valores propios de la matriz $\mathbf{A}$ son iguales.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

1. Resolver los siguientes sistemas lineales y hacer un análisis cualitativo de las soluciones.

• ${\mathbf{Y}}^{\prime }=\left(\begin{array}{cc}0& 4\\ -9& 0\end{array}\right)\mathbf{Y}$

• ${\mathbf{Y}}^{\prime }=\left(\begin{array}{cc}6& -1\\ 5& 2\end{array}\right)\mathbf{Y}$

• ${\mathbf{Y}}^{\prime }=\left(\begin{array}{cc}1& -1\\ 5& -3\end{array}\right)\mathbf{Y}$

• ${\mathbf{Y}}^{\prime }=\left(\begin{array}{cc}2& -5\\ 4& -2\end{array}\right)\mathbf{Y}$

• ${\mathbf{Y}}^{\prime }=\left(\begin{array}{cc}4& 5\\ -2& 6\end{array}\right)\mathbf{Y}$

• ${\mathbf{Y}}^{\prime }=\left(\begin{array}{cc}1& -8\\ 1& -3\end{array}\right)\mathbf{Y}$

Más adelante…

Continuando con nuestro estudio cualitativo de los sistemas lineales homogéneos con dos ecuaciones diferenciales, en la siguiente entrada veremos que ocurre en el plano fase cuando los valores propios de la matriz $\mathbf{A}$ son repetidos.

Entradas relacionadas

• Página principal del curso: Ecuaciones Diferenciales I
• Entrada anterior del curso: Teoría cualitativa de los sistemas lineales homogéneos – Valores propios reales y distintos
• Siguiente entrada del curso: Teoría cualitativa de los sistemas lineales homogéneos – Valores propios repetidos

• Video relacionado al tema: Plano fase para sistemas lineales con valores propios complejos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»