Introducción

Probablemente recuerdes de otros cursos términos que son de la forma $\sum_{k=1}^{\infty}\, a_k.$ Hacen alusión a una suma de infinitos términos. Deseamos que sea posible obtener un resultado de esta operación, pero no siempre existe. Para el caso en que los términos $a_k$ son números reales, puedes consultar las entradas Cálculo Diferencial e Integral II: Definición de series y series infinitas
Cálculo Diferencial e Integral II: Criterio de la divergencia y de acotación
Cálculo Diferencial e Integral II: Criterio de comparación y comparación del limite.

En esta sección trabajaremos con series en un espacio vectorial normado. Ya que estas se construyen a partir de sucesiones, podemos esperar que varios resultados de convergencia, vistos hasta el momento, encontrarán su versión en las sumas infinitas.

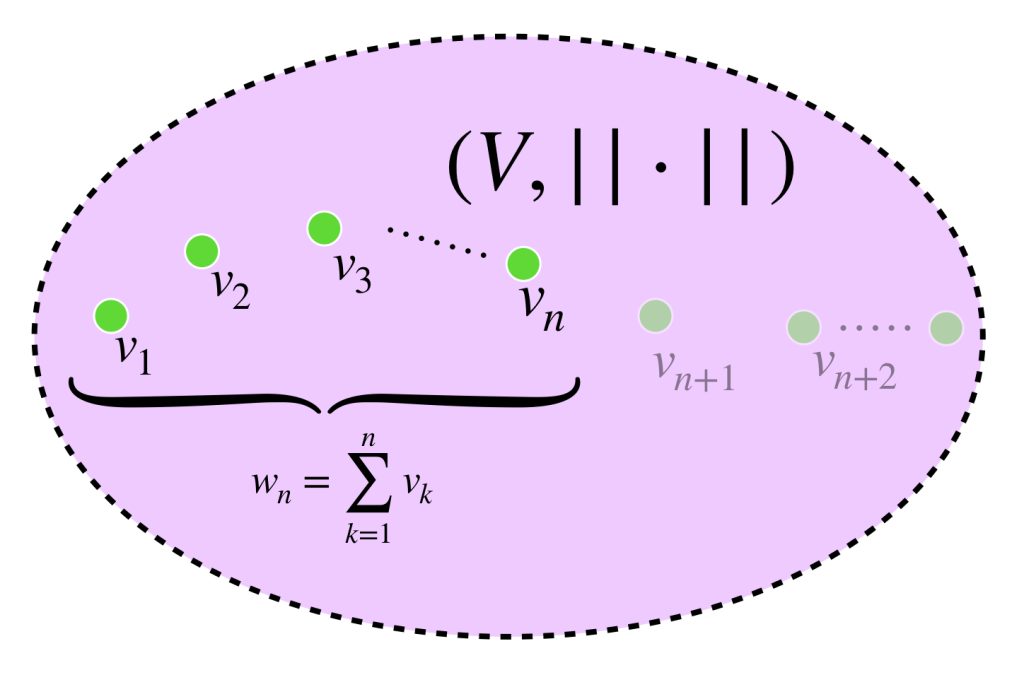
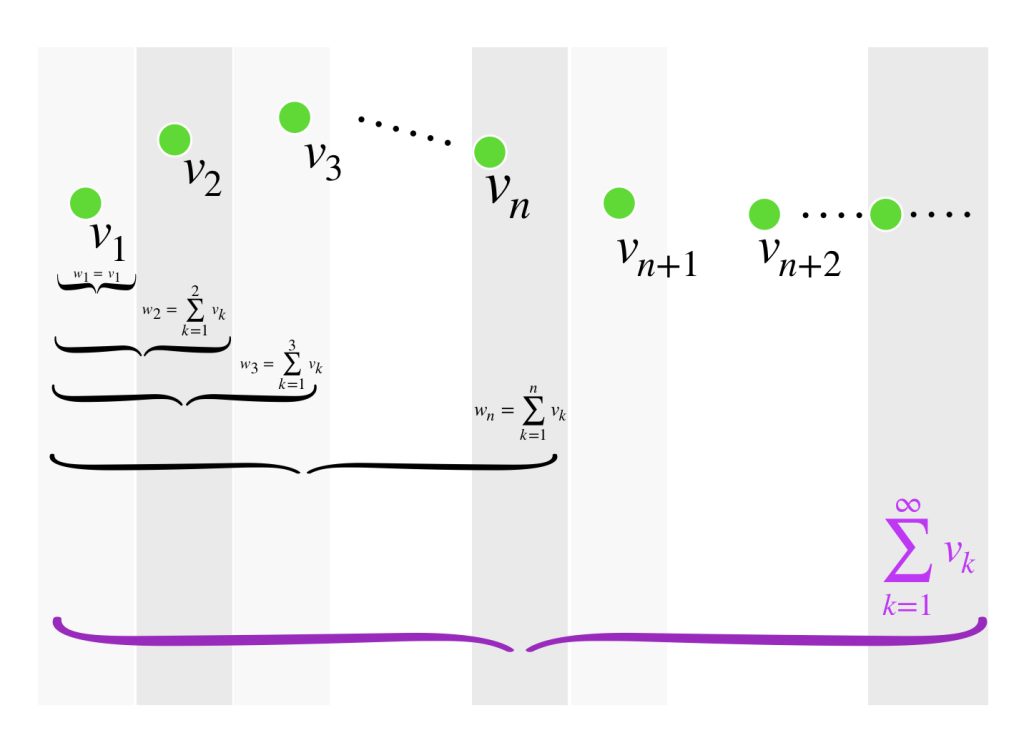
Definición. Suma parcial. Sea $V=(V, \norm{\cdot})$ un espacio vectorial normado y sea $(v_n)_{n \in \mathbb{N}} \,$ una sucesión en $V.$ Consideremos la suma de los primeros $n$ términos con $n \in \mathbb{N}.$ Se llama suma parcial y está dada por:

$$w_n:= \sum_{k=1}^{n} \, v_k.$$

Podemos pensar que conforme incrementa el valor de $n$ más términos de la sucesión son considerados en la suma. Se forma entonces una sucesión con los resultados $w_n. $ Así, $\, (w_n)_{n \in \mathbb{N}} \,$ es la sucesión de sumas parciales. ¿Será convergente?

Definición. Serie convergente. Sea $(v_n)_{n \in \mathbb{N}}$ una sucesión en $V=(V, \norm{\cdot}).$ Si la sucesión de sumas parciales $(w_n)_{n \in \mathbb{N}} \,$ converge en $V,$ decimos que la serie denotada como

$$\sum_{k=1}^{\infty} \, v_k$$

converge en $V$ y equivale al límite de las sumas parciales, es decir.

$$ \underset{n \to \infty}{lim} \, w_n \, = \, \sum_{k =1}^{\infty} \, v_k.$$

Dejaremos como ejercicio demostrar que si una serie converge, entonces su límite es único.

Se satisface la siguiente:

Proposición. Si la serie $\sum_{k=1}^{\infty} \, v_k$ converge en $V,$ entonces $(v_n)_{n \in \mathbb{N}} \,$ converge a $0$ en $V.$ Se sigue también que esta sucesión es acotada.

Demostración:
Sea $\varepsilon >0.$ Ya que $\sum_{k=1}^{\infty} \, v_k$ converge en $V,$ por definición, $(w_n)_{n \in \mathbb{N}}$ converge en $V$ y por tanto es de Cauchy, así existe $N \in \mathbb{N}$ tal que para cualesquiera $n,m \geq N,$

$$\norm{w_n-w_m} < \varepsilon$$

en particular, para cada $n \geq N$ se cumple

\begin{align*}
&&\norm{w_{n+1}-w_n} &< \varepsilon\\
&\iff& \norm{\sum_{k=1}^{n+1} v_k \, – \sum_{k=1}^{n} v_k} &< \varepsilon\\
&\iff& \norm{v_{n+1}} &< \varepsilon
\end{align*}

Por lo tanto $v_n \to 0$ en $V,$ y por lo visto en Convergencia, concluimos que $(v_n)_{n \in \mathbb{N}} \,$ es acotada.

Cuando el espacio normado $V$ es completo se tiene un resultado que muestra condiciones necesarias y suficientes para que una serie sea convergente:

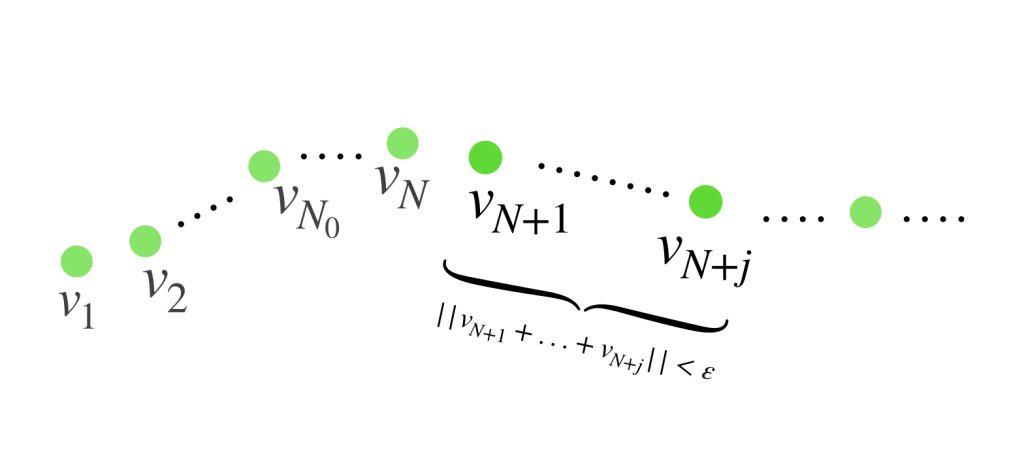
Proposición. Criterio de Cauchy para series. Sea $V$ un espacio de Banach y sea $(v_n)_{n \in \mathbb{N}} \,$ una sucesión en $V.$ La serie $\sum_{k=1}^{\infty} \, v_k$ converge en $V$ si y solo si para cada $\varepsilon >0$ existe $N_0 \in \mathbb{N}$ tal que
$$\norm{v_{N+1}+…+v_{N+j}}< \varepsilon$$
para cualquier $N \geq N_0$ y cualquier $j \geq 1.$

Demostración:
Sea $\varepsilon > 0.$ La serie $\sum_{k=1}^{\infty} \, v_k$ converge en $V$ si y solo si $(w_n)_{n \in \mathbb{N}}$ converge en $V$. Como $V$ es de Banach esto ocurre si y solo si $(w_n)_{n \in \mathbb{N}}$ es de Cauchy, es decir, si y solo si existe $N_0 \in \mathbb{N}$ tal que para cualesquiera $n,m \geq N_0,$
$$\norm{w_n -w_m} < \varepsilon$$
si y solo si para cualquier $N \geq N_0$ y cualquier $j \geq 1$, como $N+j > N \geq N_0$ se sigue que
\begin{align*}
&&\norm{w_{N+j} -w_{N}} < \varepsilon\\
&\Rightarrow &\norm{\sum_{k=1}^{N+j} v_k \, – \sum_{k=1}^{N} v_k} < \varepsilon\\
&\Rightarrow &\norm{v_{N+1}+…+v_{N+j}} < \varepsilon
\end{align*}

que es lo que queríamos demostrar.

Hay otra forma de asegurar la convergencia de una serie a partir de la convergencia de la serie formada por la norma de sus términos. Es decir:

Teorema. Criterio de Weierstrass. Sea $V$ un espacio de Banach y sea $(v_n)_{n \in \mathbb{N}} \,$ una sucesión en $V.$ Si la serie de números reales $\sum_{k=1}^{\infty} \, \norm{v_k}$ converge decimos que es absolutamente convergente. En este caso se cumple que la serie $\sum_{k=1}^{\infty} \, v_k$ converge en $V$ y además:
$$\norm{\sum_{k=1}^{\infty} \, v_k} \leq \sum_{k=1}^{\infty} \, \norm{v_k}.$$

Demostración:
Dado que $\sum_{k=1}^{\infty} \, \norm{v_k}$ converge en $\mathbb{R}$ que es de Banach, se sigue por la proposición anterior, que existe $N_0 \in \mathbb{N}$ tal que para cualquier $N \geq N_0$ y cualquier $j \geq 1$ se cumple
\begin{align*}
&&&|\, \norm{v_{N+1}}+…+\norm{v_{N+j}} \,|&< \varepsilon\\
&\Rightarrow &&\norm{v_{N+1}}+…+\norm{v_{N+j}}&< \varepsilon\\
&\Rightarrow &\norm{v_{N+1}+…+v_{N+j}}\leq &\norm{v_{N+1}}+…+\norm{v_{N+j}} &< \varepsilon.
\end{align*}

Nuevamente por la proposición anterior concluimos que la serie $\sum_{k=1}^{\infty} \, v_k$ converge en $V.$

Dado que para cada $n \in \mathbb{N}$ se cumple

\begin{align*}
&&\norm{\sum_{k=1}^{n}v_k} &\leq \sum_{k=1}^{n} \norm{v_k}\\
&\Rightarrow& \underset{n \to \infty}{lim} \, \norm{\sum_{k=1}^{n}v_k} &\leq \underset{n \to \infty}{lim} \, \sum_{k=1}^{n} \norm{v_k}\\
&\Rightarrow& \norm{\sum_{k=1}^{\infty} \, v_k} &\leq \sum_{k=1}^{\infty} \, \norm{v_k}.
\end{align*}

Con lo cual concluimos la demostración. Este teorema tiene su regreso en la siguiente:

Proposición. Sea $(V, \norm{\cdot})$ un espacio vectorial normado. Entonces $V$ es completo si y solo si toda serie en $V$ absolutamente convergente es convergente. La demostración del regreso se dejará como ejercicio.

Más adelante…

Ya que nos familiarizamos con la idea de las sumas infinitas, procederemos con unas que tendrán como términos funciones. Debido a que la suma de funciones es una función, de esta naturaleza será el límite.

Tarea moral

1. Demuestra que si una serie de un espacio vectorial normado es convergente, entonces su límite es único.
2. Sea $(V, \norm{\cdot})$ un espacio vectorial normado. Prueba que si toda serie en $V$ absolutamente convergente es convergente entonces $V$ es completo. A continuación una guía para la demostración:
   a) Sea $(v_n)_{n \in \mathbb{N}}$ una sucesión de Cauchy en $V.$ Construye una subsucesión $(v_{nk})$ de $(v_n)$ tal que $\norm{x_{n_{k+1}}-x_{nk}}< \frac{1}{2^k}.$
   b) Prueba que $sum_{k=1}^{\infty}(x_{n_{k+1}}-x_{nk})$ es convergente.
   c) Prueba que $(v_{nk})$ converge y concluye que $(v_n)$ es convergente.

Enlaces:

• Análisis Matemático.
• Enlace a entrada anterior.
• Enlace a entrada siguiente.