$ \textit{ MATERIAL EN REVISIÓN}$
Introducción:
En esta ocasión nos vamos a fijar en colecciones de conjuntos que están contenidos unos en otros. Vamos a suponer que es una cantidad numerable de conjuntos. El primer conjunto contiene al segundo, que a su vez contiene a un tercero y así, sucesivamente.
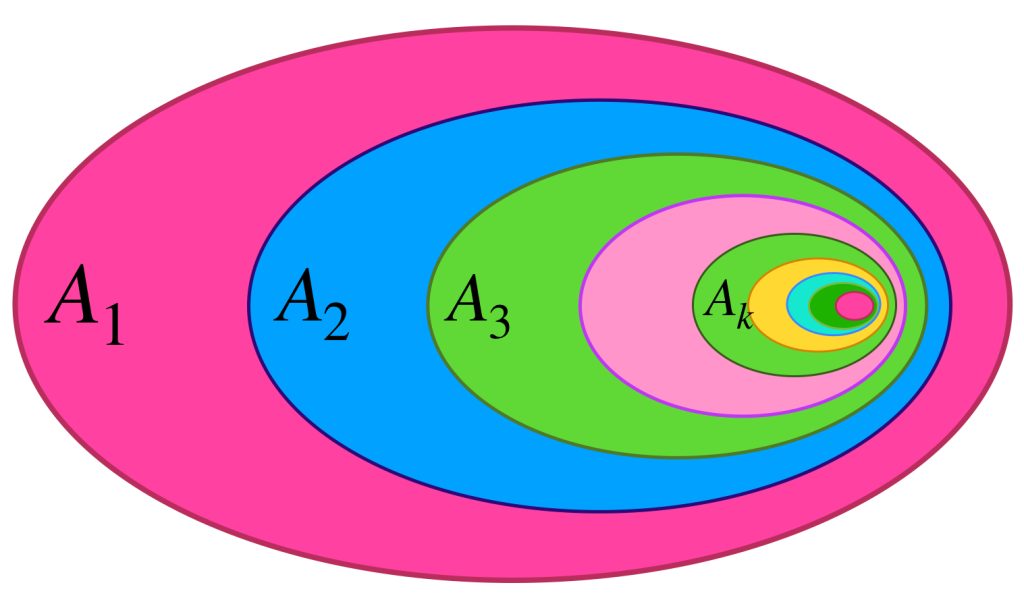
Ahora pensemos en la intersección de todos esos conjuntos. Intuitivamente podemos visualizar que se tratará de un conjunto muy pequeño, que estará contenido en todos los demás.
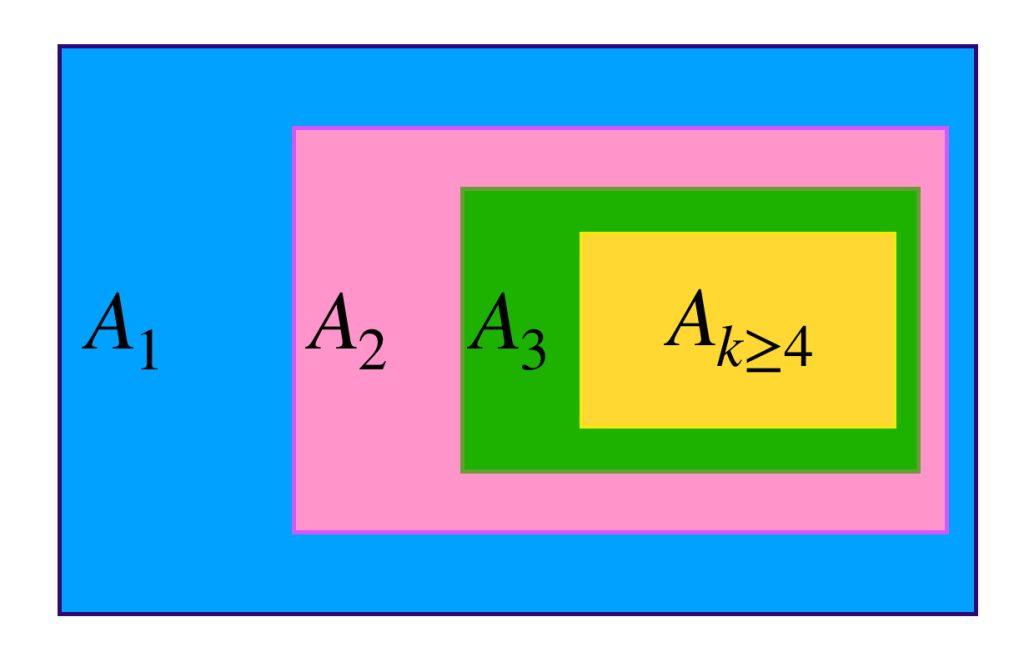
Aquí tenemos un ejemplo de una sucesión de conjuntos donde los últimos términos corresponden al mismo conjunto. La intersección de todos los conjuntos es, evidentemente, ese último conjunto
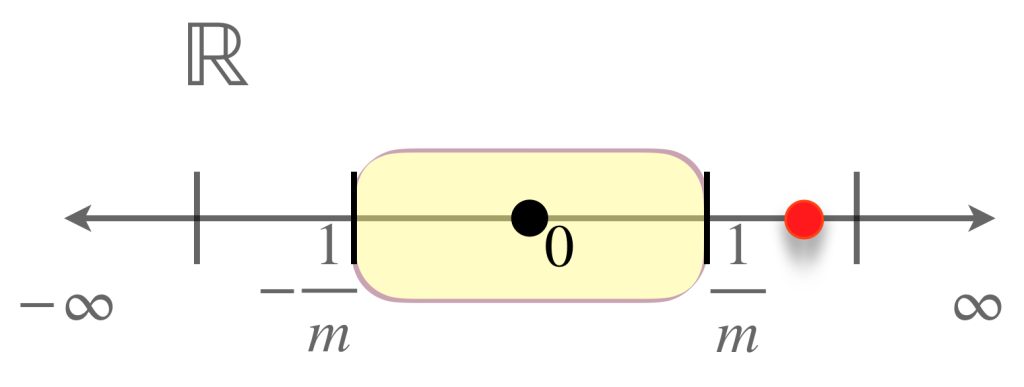
Observemos la sucesión de intervalos $[-\frac{1}{n},\frac{1}{n}]_{n \in \mathbb{N}}.$
Nota que todos tienen como elemento al cero. Además es el único elemento que pertenece a la intersección de todos los intervalos, pues si suponemos que hay otro más, dado que $\frac{1}{n} \to 0$ es posible encontrar un intervalo suficientemente pequeño, que deje fuera este elemento.
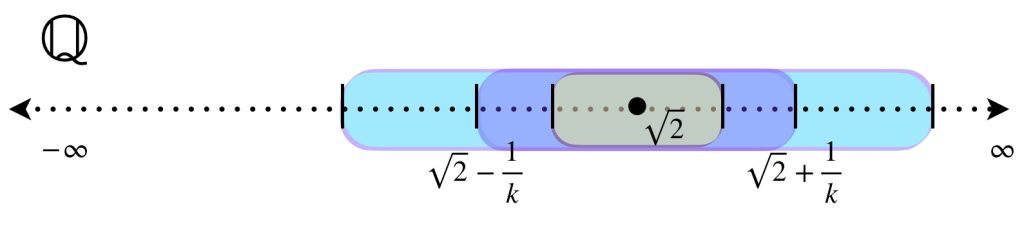
Ahora consideremos el subespacio $\mathbb{Q}$ con la métrica usual. En esta ocasión los intervalos serán $(\sqrt{2}-\frac{1}{n},\sqrt{2}+\frac{1}{n}), \, n \in \mathbb{N}.$ Queda como ejercicio al lector demostrar que la intersección de estos conjuntos es vacía en $\mathbb{Q}.$
Entonces, ¿bajo qué condiciones podremos asegurar que la intersección no es vacía pese a que los conjuntos se hagan «cada vez más pequeños» y estén contenidos unos en otros? Veamos la siguiente definición:
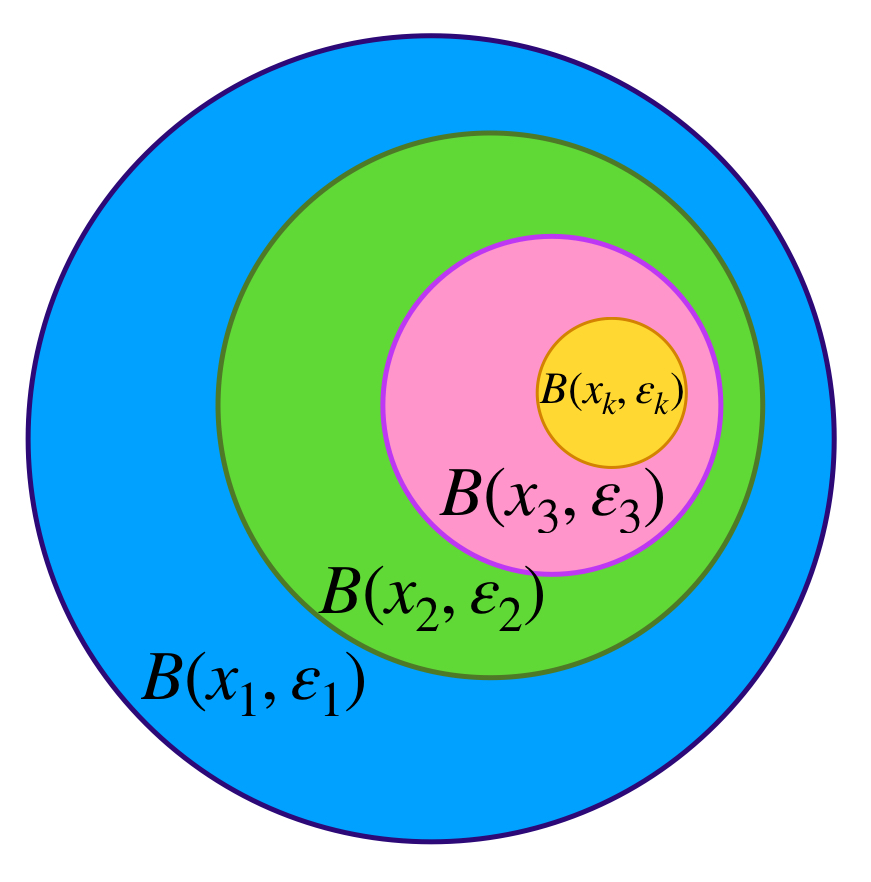
Definición. Bolas encajadas. Sea $(X,d)$ un espacio métrico y $(\overline{B}(x_n,\varepsilon_n))_{n \in \mathbb{N}} \,$ una sucesión de bolas cerradas en $X.$ Si para toda $ n \in \mathbb{N}$ se cumple que $\overline{B}(x_{n+1},\varepsilon_{n+1}) \subset \overline{B}(x_{n},\varepsilon_{n})$ diremos que la sucesión $(\overline{B}(x_n,\varepsilon_n))_{n \in \mathbb{N}} \,$ es de bolas encajadas.
Proposición. Principio de bolas encajadas. $(X,d)$ es un espacio métrico completo si y solo si para cualquier sucesión de bolas cerradas encajadas $(\overline{B}(x_n,\varepsilon_n))_{n \in \mathbb{N}} \,$ cuyos radios tienden a cero, es decir $\varepsilon_n \to 0,$ se cumple que la intersección de todas las bolas cerradas es no vacía. Además $\underset{n \in \mathbb{N}}{\cap} \, \overline{B}(x_n,\varepsilon_n) = \{x\}$ para algún $x \in X.$
Demostración:
Supongamos que $(X,d)$ es completo. Sea $(\overline{B}(x_n,\varepsilon_n))_{n \in \mathbb{N}} \,$ una sucesión de bolas encajadas cuyos radios tienden a cero. Vamos a probar primero que la sucesión de los centros de las bolas cerradas $(x_n)_{n \in \mathbb{N}} \,$ es de Cauchy. Sea $\varepsilon > 0,$ como $\varepsilon_n \to 0,$ existe $N \in \mathbb{N}$ tal que para toda $ \, n \geq N, \, \varepsilon_n < \frac{\varepsilon}{2}.$ Como la sucesión es de bolas encajadas, tenemos que para cada $ \, l,m \geq N, \, \overline{B}(x_l,\varepsilon_l) \subset \overline{B}(x_N,\varepsilon_N)$ y $\overline{B}(x_m,\varepsilon_m) \subset \overline{B}(x_N,\varepsilon_N)$ entonces $d(x_l,x_m) \leq d(x_l,x_N) + d(x_N,x_m) < \frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon.$ Por lo tanto $(x_n)$ es de Cauchy. Como $X$ es completo, se sigue que $x_n \to x$ para algún $x \in X.$
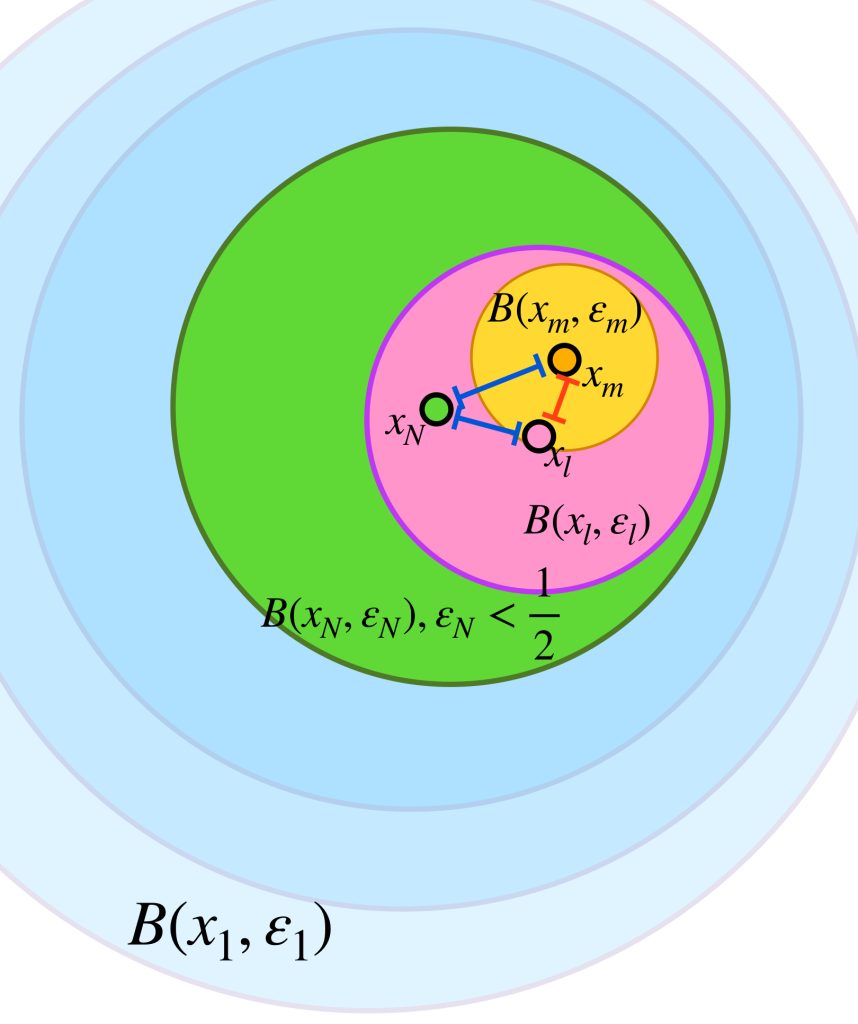
Vamos a demostrar que $x \in \underset{n \in \mathbb{N}}{\cap} \, \overline{B}(x_n,\varepsilon_n).$ Sea $n \in \mathbb{N}.$ Como las bolas son encajadas, tenemos que para toda $ k \geq n, \, \overline{B}(x_k,\varepsilon_k) \subset \overline{B}(x_n,\varepsilon_n)$ en consecuencia para toda $ k \geq n,$ el término de la sucesión $x_k$ es elemento de $\overline{B}(x_n,\varepsilon_n),$ que es un conjunto cerrado. Ya que la subsucesión formada por estos últimos términos converge en $x$ se sigue de lo que vimos en Convergencia que $x \in \overline{B}(x_n,\varepsilon_n).$ Como esto ocurre para cada $ n \in \mathbb{N},$ concluimos que $x \in \underset{n \in \mathbb{N}}{\cap} \, \overline{B}(x_n,\varepsilon_n).$
Además $x$ es el único punto en la intersección, pues si existe otro punto $x’ \in \underset{n \in \mathbb{N}}{\cap} \, \overline{B}(x_n,\varepsilon_n)$ existen también bolas cerradas suficientemente pequeñas que no contienen a ambos puntos. La demostración de este hecho se deja como ejercicio.
Para el regreso buscamos demostrar que $(X,d)$ es completo. Sea $(x_n)_{n \in \mathbb{N}} \,$ una sucesión de Cauchy.
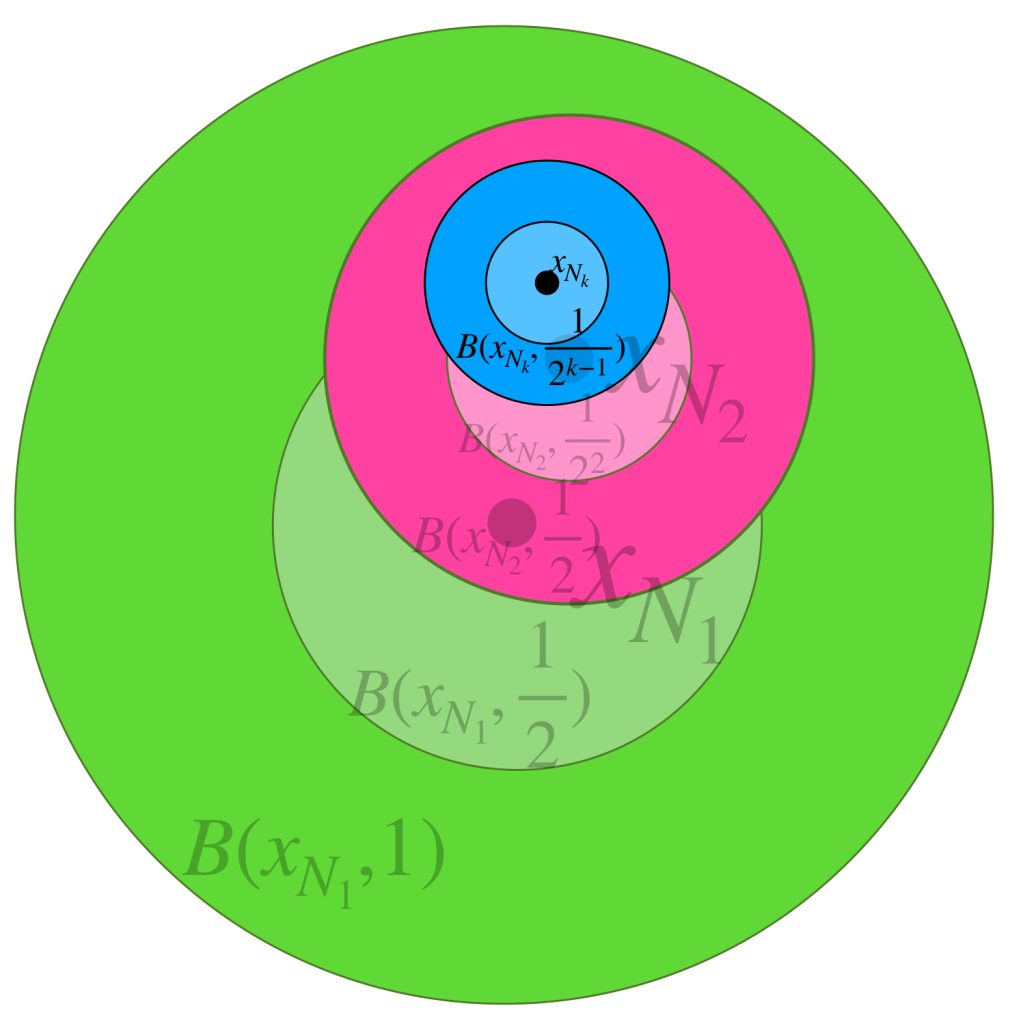
Vamos a construir una sucesión de bolas encajadas de la siguiente forma:
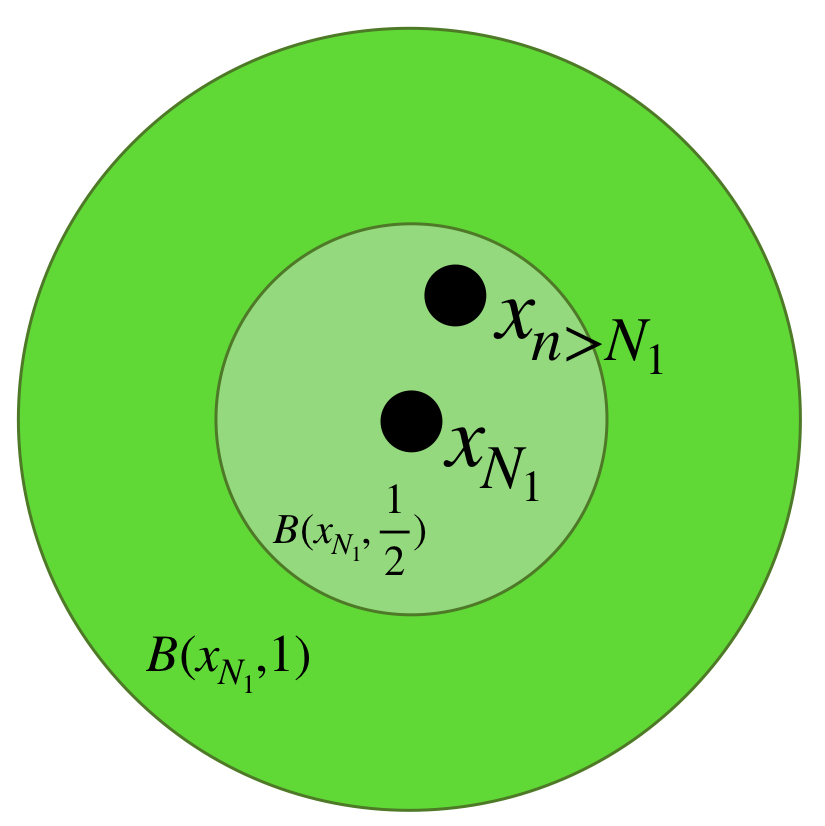
Ya que la sucesión $(x_n)$ es de Cauchy, podemos afirmar que existe $N_1 \in \mathbb{N}$ tal que para cada $ \, n,m \geq N_1, \, d(x_n,x_m) < \frac{1}{2}.$ Entonces para toda $ \, n \geq N_1, \, x_n \in \overline{B}(x_{N_1}, \frac{1}{2}) \subset \overline{B}(x_{N_1},1).$
Nuevamente, como $(x_n)$ es de Cauchy, existe $N_2 \in \mathbb{N}$ tal que para cada $ \, n,m \geq N_2, \, d(x_n,x_m) < \frac{1}{2^2}.$ Entonces para toda $ \, n \geq N_2, \, x_n \in \overline{B}(x_{N_2}, \frac{1}{2^2}) \subset \overline{B}(x_{N_2},\frac{1}{2}).$ Nota que esta bola está contenida en la anterior.
Continuando recursivamente, la bola $k$ de la sucesión en construcción estará dada por el centro $x_{N_k}$ donde $N_k$ es tal que para toda $ \, n,m \geq N_k, \, d(x_n,x_m) < \frac{1}{2^k}.$ Entonces para toda $ \, n \geq N_k, \, x_n \in \overline{B}(x_{N_k}, \frac{1}{2^k}) \subset \overline{B}(x_{N_k},\frac{1}{2^{k-1}}).$
Así, la sucesión $(\overline{B}(x_{N_n},\frac{1}{2^{n-1}}))_{n \in \mathbb{N}} \,$ es de bolas encajadas y sus radios tienden a cero. Por hipótesis sabemos que la intersección de estos conjuntos es $\{x\},$ para algún $x \in X.$ Es sencillo probar que la sucesión de centros $(x_{N_n})_{n \in \mathbb{N}} \,$ converge en $x$ (se dejará como ejercicio). Entonces tenemos una subsucesión de la sucesión de Cauchy $(x_n)$ que es convergente y, como vimos en entrada anterior, esto demuestra que $(x_n) \to x$ por lo que $X$ es completo.
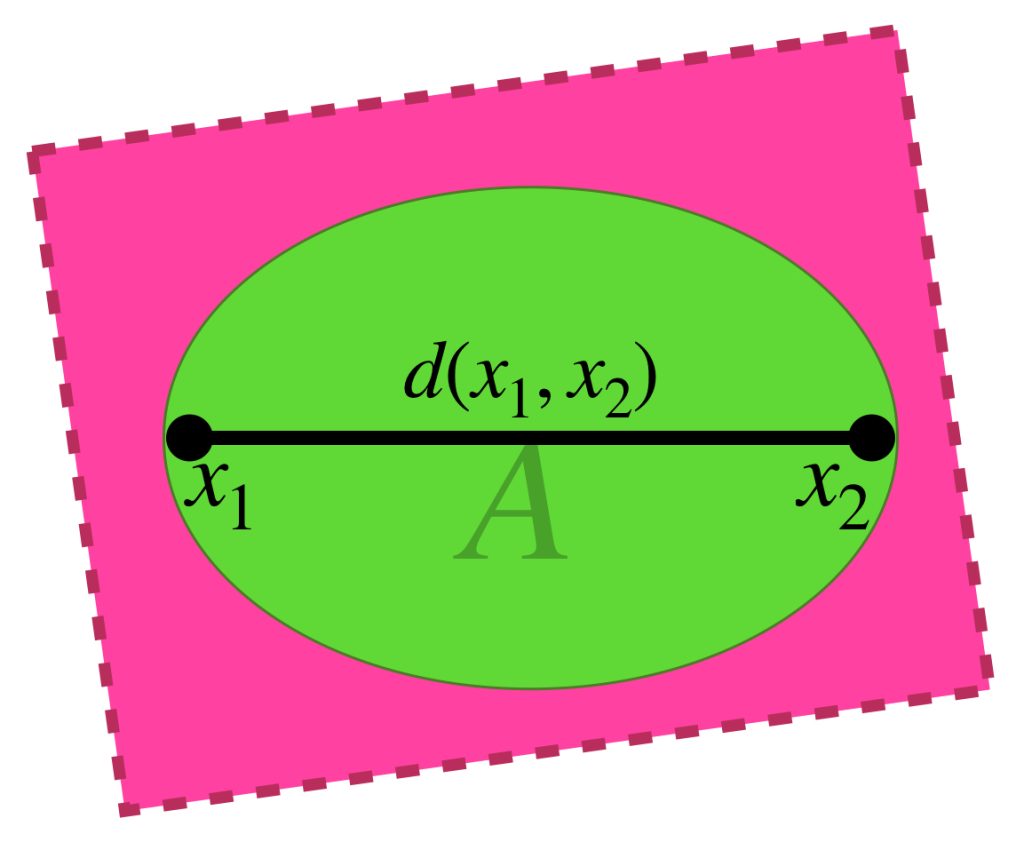
Notemos que para asegurar la contención de un conjunto en otro, necesitamos obtener información acerca de las distancias entre sus elementos. Esto motiva una definición para conjuntos más generales que una bola cerrada:
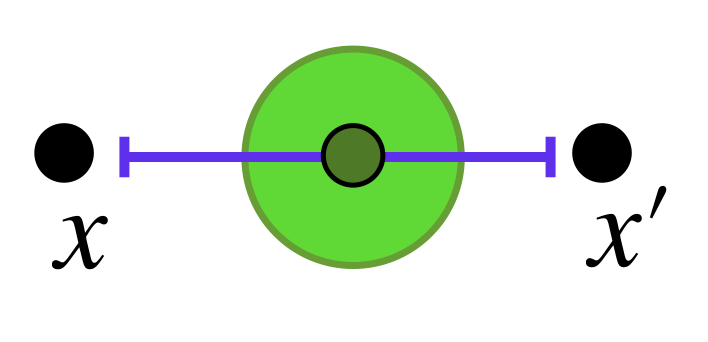
Definición. Diámetro de un conjunto. Sea $A \subset X.$ Entonces el diámetro de $A$ se define como:
$$diam(A) := sup\{d(x_1,x_2) \,| \, x_1,x_2 \in A \}.$$
Cuando el conjunto $\{d(x_1,x_2) \, | \, x_1,x_2 \in A \}$ no es acotado, diremos que el diámetro es $\infty.$
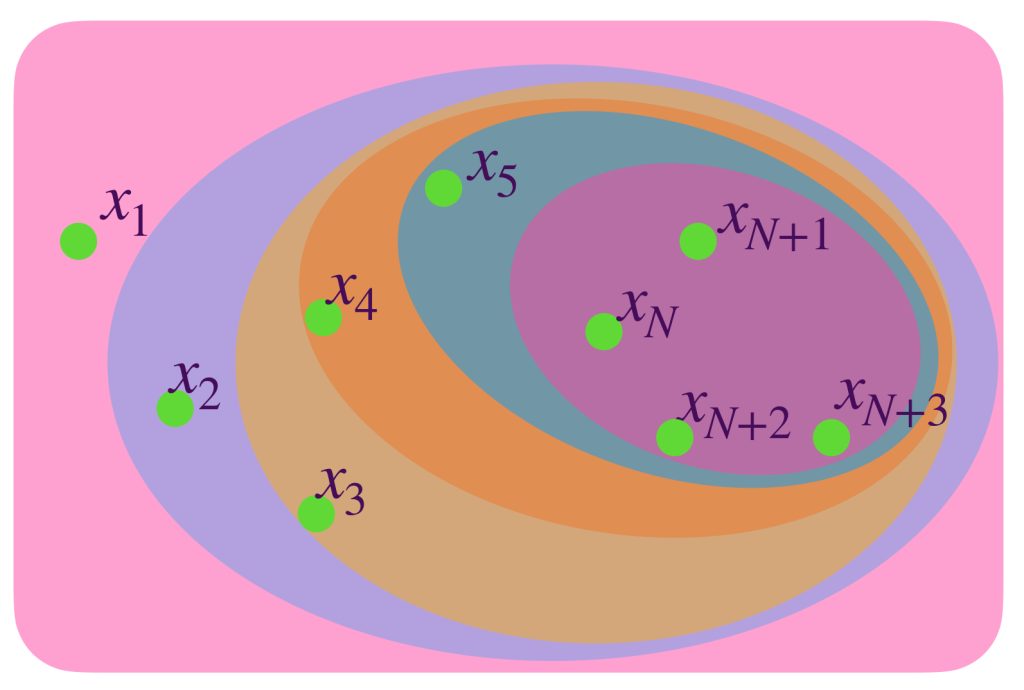
Proposición. Sea $(x_n)_{n \in \mathbb{N}} \,$ una sucesión en $(X,d)$ y para cada $N \in \mathbb{N}, \, X_N:=\{x_k \, | \, k\geq N\}$ el conjunto de los términos de la sucesión que van a partir de $x_N.$ Entonces $(x_n)$ es una sucesión de Cauchy si y solo si
$$\underset{N \to \infty}{lim}\, diam \, (X_N)=0$$
Demostración:
Supón que $(x_n)$ es una sucesión de Cauchy en $X$ y sea $\varepsilon>0.$ Entonces existe $K \in \mathbb{N}$ tal que para toda $ \, l,m \geq K, \, d(x_l,x_m)<\varepsilon.$ En consecuencia $diam\,(X_K) \leq \varepsilon.$ Como para todo $L \geq K, \, (X_L) \subset (X_K)$ se sigue que para todo $L \geq K, \, diam(X_L) \leq diam(X_K) \leq \varepsilon.$ Por lo tanto $\underset{N \to \infty}{lim}\, diam \, (X_N)=0$
Ahora supongamos que $\underset{N \to \infty}{lim}\, diam \, (X_N)=0.$ Buscamos demostrar que $(x_n)$ es de Cauchy. Sea $\varepsilon >0$, como los diámetros tienden a cero, existe $K \in \mathbb{N}$ tal que en particular $(X_K)$ satisface que $diam \, (X_K) < \varepsilon.$ Entonces para toda $ \, l,m \geq K, \, d(x_l,x_m) < \varepsilon$ lo cual demuestra que $(x_n)$ es de Cauchy.
Terminemos con la siguiente:
Proposición. Sean $(A_n)_{n \in \mathbb{N}}\,$ una sucesión de subconjuntos cerrados de un espacio métrico completo $(X,d)$ tales que para todo $n \in \mathbb{N}, \, A_{n+1} \subset A_{n}$ y además $\underset{n \to \infty}{lim} \, diam(A_n) \to 0.$ Entonces $\underset{n \in \mathbb{N}}{\cap}A_n=\{x\}$ para algún $x \in X.$
Demostración:
Para cada $n \in \mathbb{N}$ elegimos $x_n \in A_n.$ Entonces para cada $N \in \mathbb{N}$ el conjunto $X_N$ definido en la proposición anterior está contenido en $A_N$, pues los conjuntos están anidados. En consecuencia, $diam(X_N) \leq diam(A_n) \to 0.$ La proposición anterior nos permite concluir que $(x_n)$ es una sucesión de Cauchy. Como $X$ es completo, se sigue que $(x_n) \to x$ para algún $x \in X.$ Dejamos como ejercicio demostrar que $\underset{n \in \mathbb{N}}{\cap}A_n=\{x\}.$
¿Recuerdas la distancia de Hausdorff vista en La métrica de Hausdorff? Nota que si $A$ y $B$ son subconjuntos de $X$ entonces $d_H(A,B)\leq diam(A \cup B).$ En esa misma entrada vimos que conjuntos anidados convergen a la intersección de todos ellos, y que este conjunto está formado por los puntos de convergencia de sucesiones que tienen elementos en los conjuntos anidados. En entradas futuras veremos que los espacios compactos son cerrados. ¿Cómo justificarías las proposiciones vistas en esta entrada a partir de los resultados presentados en la métrica de Hausdorff?
Más adelante…
Veremos los conceptos de conjunto denso y conjunto nunca denso. Descubriremos un resultado que ha sido muy importante en el estudio de los espacios métricos completos: El teorema de Baire.
Tarea moral
- Sea $\mathbb{Q}$ el subespacio de $\mathbb{R}$ con la métrica usual. Demuestra que la intersección de los intervalos $[\sqrt{2}-\frac{1}{n},\sqrt{2}+\frac{1}{n}], \, n \in \mathbb{N}$ es vacía en $\mathbb{Q}.$
- Demuestra que si $x$ está en la intersección de bolas encajadas $\underset{n \in \mathbb{N}}{\cap} \, \overline{B}(x_n,\varepsilon_n)$ entonces es único.
- Demuestra que la sucesión de centros $(x_{N_n})_{n \in \mathbb{N}} \,$ de la proposición converge en $x.$
- Sea $A \subset X.$ Demuestra que $diam(A)=diam(\overline{A}).$
- Con respecto a la última proposición, demuestra que $\underset{n \in \mathbb{N}}{\cap}A_n=\{x\}.$
- Da un ejemplo de un espacio métrico completo y de una sucesión de bolas cerradas en este espacio, encajadas unas en otras que tenga intersección vacía.
Bibliografía
- Kolmogorov, A.N., Fomin, S.V., Elementos de la Teoría de Funciones y del Análisis Funcional. (2a ed.). Moscú: Editorial MIR, 1975. Págs: 74 y 75.