Introducción
De las clases en el bachillerato recordarás las siguientes definiciones, utilizando el triángulo rectángulo de la imagen siguiente:
\begin{align*}
sen\theta&=\frac{\text{cat op}}{\text{hip}}=\frac{b}{c} & csc\theta&=\frac{\text{hip}}{\text{cat op}}=\frac{c}{b}\\
cos\theta&=\frac{\text{cat ad}}{\text{hip}}=\frac{a}{c} & sec\theta&=\frac{\text{hip}}{\text{cat ad}}=\frac{c}{a}\\
tan\theta&=\frac{\text{cat op}}{\text{cat ad}}=\frac{b}{a} & cot\theta&=\frac{\text{cat ad}}{\text{cat op}}=\frac{a}{b}\\
\end{align*}
donde:
cat op = cateto opuesto ; cat ad = cateto adyacente e hip= hipotenusa.
También recordemos que tenemos la siguiente equivalencia:
$360°$ es equivalente a $2\pi$.
A lo largo de esta entrada veremos las principales características de este conjunto de funciones, sus gráficas y algunas identidades trigonométricas.
Identidades trigonométricas Pitagóricas
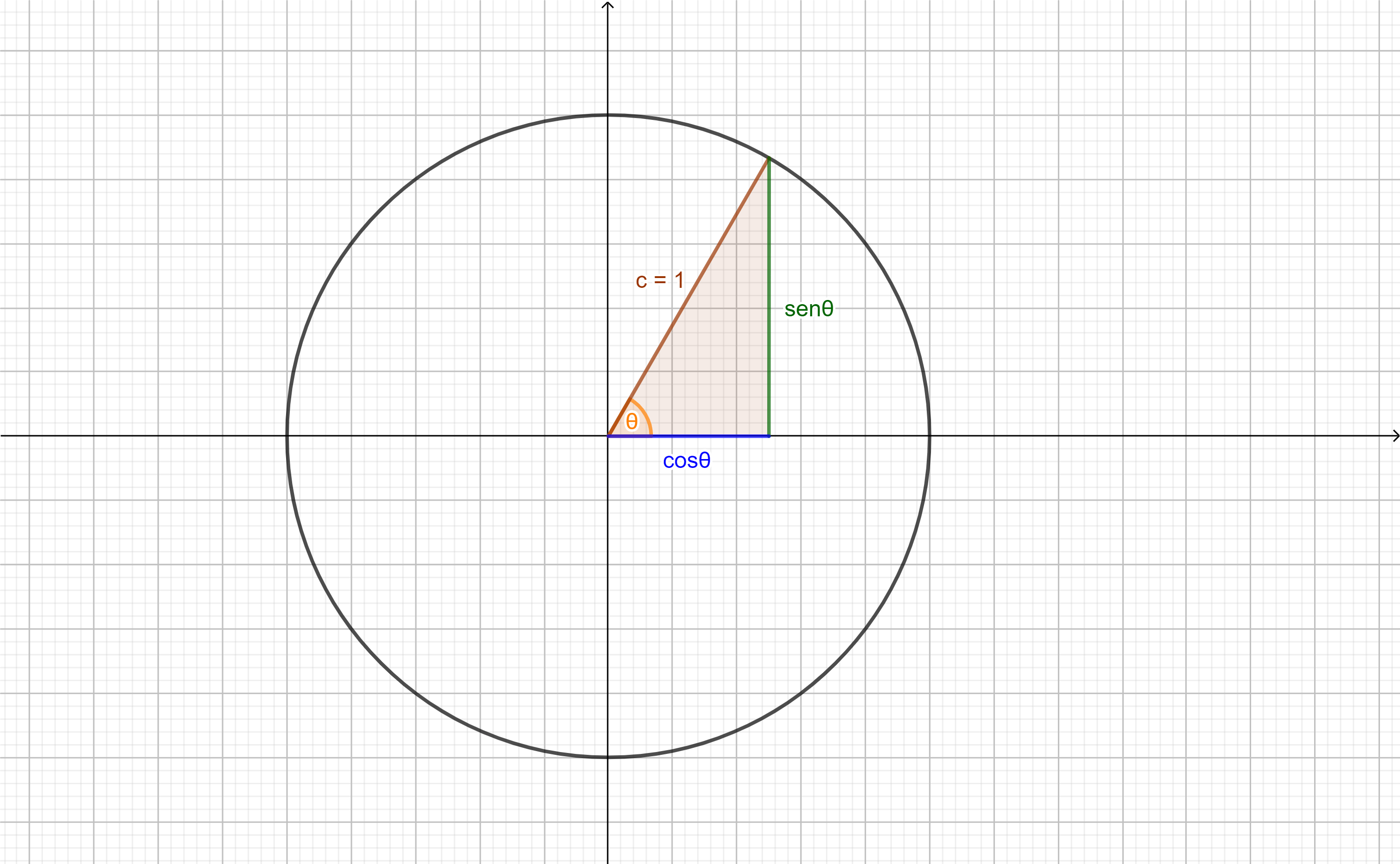
Si tomamos a la circunferencia unitaria y un triángulo rectángulo como en la imagen:
Observamos que al sustituir el valor hip $=1$ en las definiciones anteriores para el $sen\theta$ y el $cos\theta$ tenemos:
\begin{align*}
sen\theta&=\frac{\text{cat op}}{\text{1}} & cos\theta&=\frac{\text{cat ad}}{\text{1}}\\
&= \text{cat op} & &=\text{cat ad}\\
&= b & &=a\
\end{align*}
Dadas las igualdades obtenidas e hip$=1$ al sustituir para el resto de las funciones tenemos:
\begin{align*}
tan\theta &= \frac{sen\theta}{cos\theta} & cot\theta &=\frac{cos\theta}{sen\theta}\\
sec\theta &=\frac{1}{cos\theta} & csc\theta&=\frac{1}{sen\theta}
\end{align*}
Recordemos el conocido Teorema de Pitágoras que nos da una relación entre los catetos y la hipotenusa de un triángulo rectángulo:
$$a^{2}+b^{2}=c^{2}.$$
Si lo aplicamos al triángulo rectángulo obtenido en la imagen anterior donde:
\begin{align*}
a&= cos\theta & b&=sen\theta & c&=1
\end{align*}
entonces tenemos la siguiente igualdad:
\begin{equation}
cos^{2}\theta + sen^{2}\theta =1.
\end{equation}
Si dividimos $(1)$ entre $cos^{2}\theta$ obtenemos:
\begin{equation*}
\frac{cos^{2}\theta}{ cos^{2}\theta}+ \frac{sen^{2}\theta}{cos^{2}\theta} =\frac{1}{cos^{2}\theta}.
\end{equation*}
Que simplificando sería:
\begin{equation}
1+ tan^{2}\theta=sec^{2}\theta.
\end{equation}
Ahora bien si decidimos dividir $(1)$ entre $sen^{2}\theta$:
\begin{equation*}
\frac{cos^{2}\theta}{sen^{2}\theta} + \frac{sen^{2}\theta}{sen^{2}\theta} =\frac{1}{sen^{2}\theta}.
\end{equation*}
Que finalmente sería:
\begin{equation}
cot^{2}\theta +1= csc^{2}\theta.
\end{equation}
Las igualdades $(1)$, $(2)$ y $(3)$ son llamadas Identidades Pitagóricas:
\begin{align*}
cos^{2}\theta + sen^{2}\theta &=1,\\
1+ tan^{2}\theta &=sec^{2}\theta,\\
cot^{2}\theta +1&= csc^{2}\theta.\\
\end{align*}
Otras identidades trigonométricas
Otras identidades trigonométricas que son de utilidad son las de suma de ángulos:
\begin{align*}
cos( \alpha + \beta)&=cos(\alpha) cos(\beta) – sen(\alpha) sen(\beta),\\
sen(\alpha + \beta)&= cos(\alpha) sen(\beta) + cos(\beta) sen(\alpha).
\end{align*}
Para la resta de ángulos tendríamos un par similar:
\begin{align*}
cos( \alpha -\beta)&=cos(\alpha) cos(\beta) + sen(\alpha) sen(\beta),\\
sen(\alpha – \beta)&= cos(\alpha) sen(\beta) – cos(\beta) sen(\alpha).
\end{align*}
Ahora veremos cómo obtener las identidades para los ángulos dobles:
\begin{align*}
cos(2\alpha)&= cos(\alpha + \alpha)\\
&= cos(\alpha) cos(\alpha) – sen(\alpha) sen(\alpha)\\
&= cos^{2}\alpha – sen^{2}\alpha
\end{align*}
Por lo tanto tendríamos para el coseno de $2\alpha$:
\begin{equation}
cos(2\alpha)=cos^{2}\alpha – sen^{2}\alpha.
\end{equation}
Si procedemos análogamente para el seno de $2\alpha$:
\begin{align*}
sen(2\alpha)&= sen(\alpha + \alpha)\\
&= cos(\alpha) sen(\alpha) + cos(\alpha) sen(\alpha)\\
&= 2sen(\alpha) cos(\alpha)
\end{align*}
Así concluimos que:
\begin{equation}
sen(2\alpha)=2sen(\alpha) cos(\alpha).
\end{equation}
También tenemos un par de identidades que relacionadas con el $sen^{2}\theta$ y el $cos^{2}\theta$:
\begin{align*}
sen^{2}\theta &= \frac{1}{2}(1-cos(2\theta)), & cos^{2}\theta& =\frac{1}{2}(1+ cos(2\theta)).\\
\end{align*}
Se dejará como ejercicios en la Tarea moral obtener este par de igualdades.
Simetrías
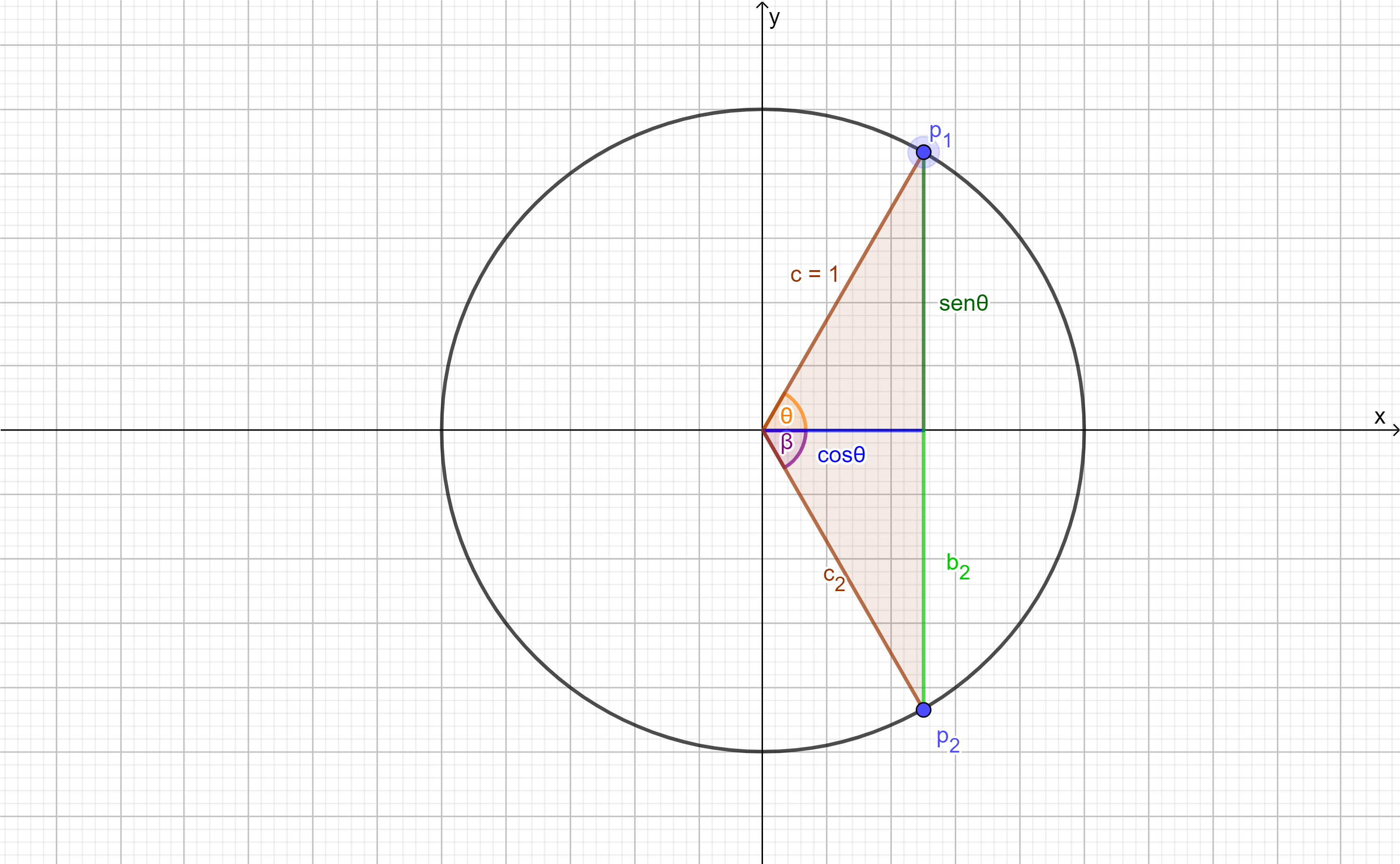
Retomando la imagen anterior, si ahora reflejamos al triángulo respecto al eje $x$, tenemos lo siguiente:
donde observamos los siguiente:
\begin{align*}
\beta &= – \theta & c_{2}&=1 & b_{2}=sen(-\theta)\\
\end{align*}
Así al considerar a los puntos $p_{1}$ y $p_{2}$ tenemos que estarían definidos de la siguiente manera:
\begin{align*}
p_{1}&=(cos(\theta), sen(\theta)) & p_{2}&=(cos(-\theta), sen(-\theta))\\
\end{align*}
Resaltamos para $p_{2}$ que:
$$p_{2}=(cos(-\theta), sen(-\theta))=(cos(\theta), -sen(\theta)).$$
de esta igualdad podemos determinar si las funciones seno y coseno son pares o impares, este ejercicio formará parte de la Tarea moral.
Función periódica
Definición (función periódica): Decimos que una función $f$ es periódica si existe $N \in \r$ tal que para todo $x \in D_{f}$ cumple que:
$$f(x)=f(x+ N)$$
y $|N|$ se llama periodo de $f$.
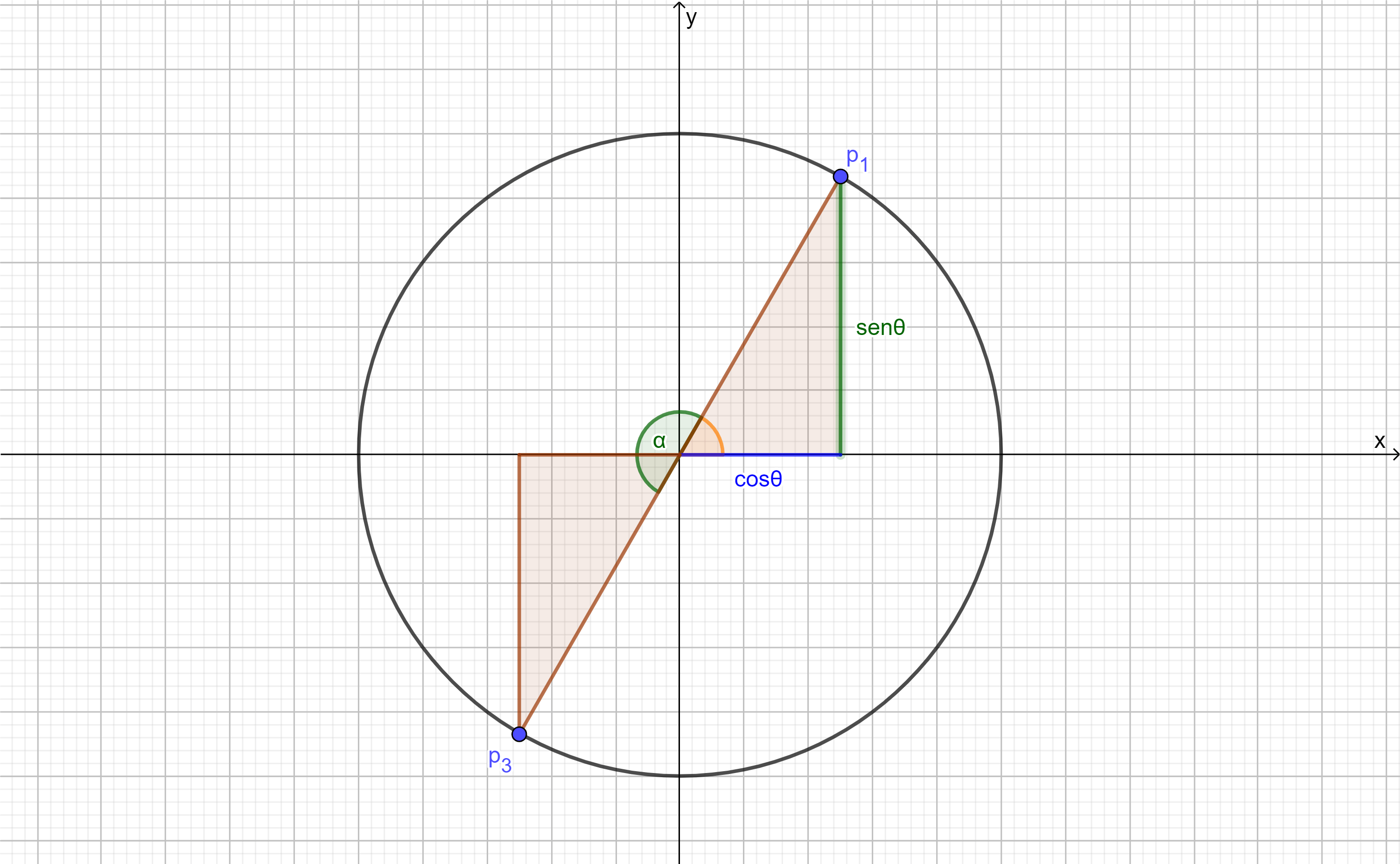
En la siguiente imagen observamos que $\alpha = \pi$ por lo que tendríamos que el nuevo triángulo agregado es en realidad el original rotado:
Así tendríamos la siguiente definición para los puntos $p_{1}$ y $p_{3}$:
\begin{align*}
p_{1}&=(cos(\theta), sen(\theta)) & p_{3}&=(cos(\theta + \pi), sen(\theta+ \pi))\\
\end{align*}
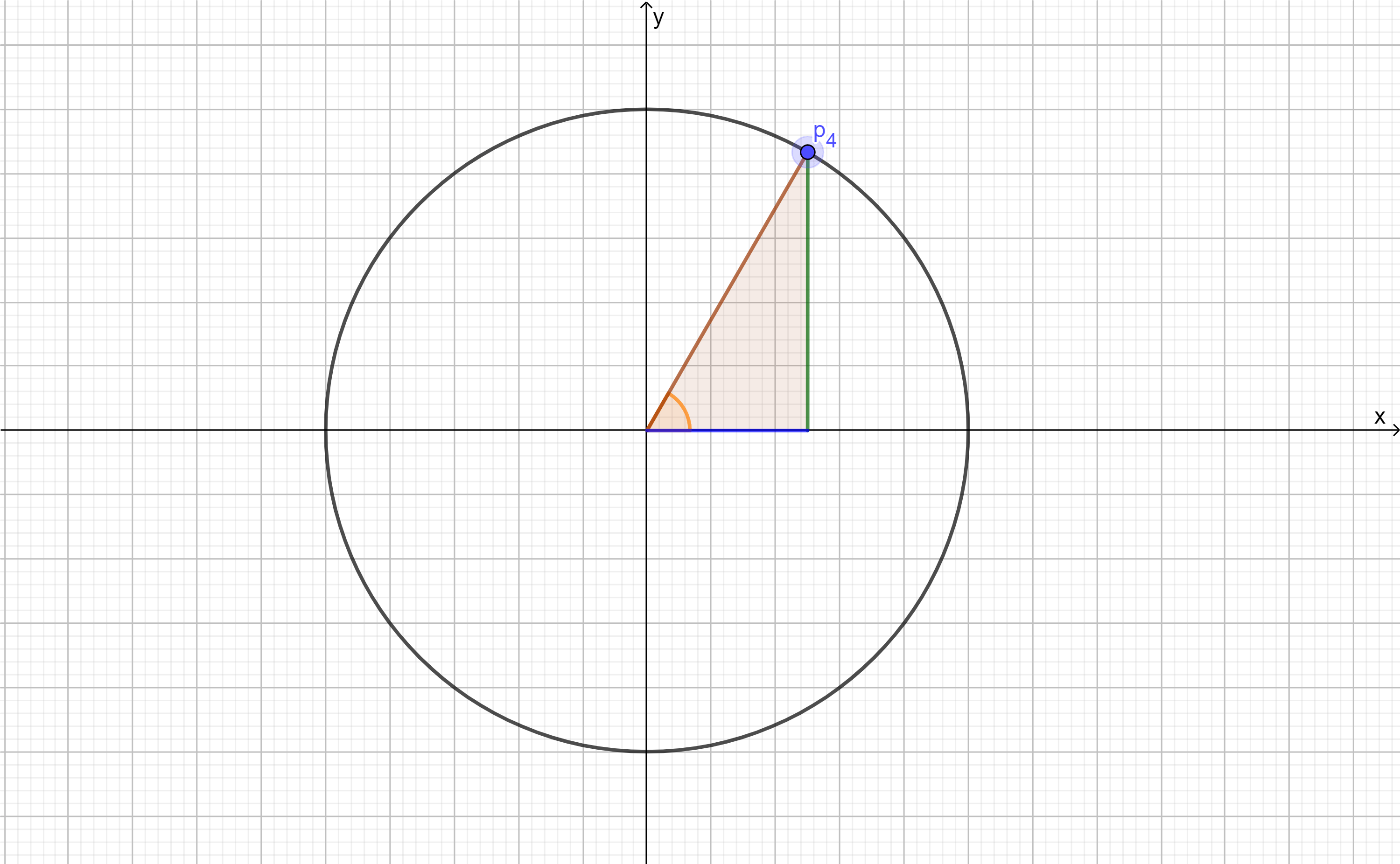
Si rotamos el triángulo ahora $\alpha = 2\pi$ tenemos que $p_{4}$ estaría definido como:
$$p_{4}=(cos(\theta + 2\pi), sen(\theta+ 2\pi)).$$
¡Y observamos que obtenemos el triángulo original! Consecuentemente tenemos las siguientes igualdades:
\begin{align*}
sen(\theta)&=sen(\theta+2\pi),\\
cos(\theta)&=cos(\theta+ 2\pi).
\end{align*}
Aplicando la definición decimos que las funciones seno y coseno son periódicas con periodo $N=2\pi$.
En las gráficas de las funciones observamos el comportamiento anterior, cada $2 \pi$ se comienzan a repetir los valores:
Observación: Vemos que para todo $x \in \r$ ocurre:
$$-1 \leq sen(x) \leq 1$$
$$-1 \leq cos(x) \leq 1$$
por lo que las funciones seno y coseno son acotadas.
Consideraremos los siguientes dominios donde cada una de las funciones cumple ser inyectiva :
\begin{align*}
sen: \left[-\frac{\pi}{2}, \frac{\pi}{2} \right] \rightarrow [-1,1]
\end{align*}
\begin{align*}
cos: [0, \pi] \rightarrow [-1,1]
\end{align*}
Más adelante
En la próxima entrada, continuaremos con las definiciones de las funciones tangente, cotangente, secante y cosecante. Por lo tanto, realizaremos un análisis similar al dado para las funciones seno y coseno.
Tarea moral
- Obtener las siguientes identidades trigonométricas:
- $$sen^{2}\theta = \frac{1}{2}(1-cos(2\theta)).$$
- $$cos^{2}\theta =\frac{1}{2}(1+ cos(2\theta)).$$
- $$tan(\alpha + \beta)=\frac{tan(\alpha) + tan(\beta)}{-tan(\alpha)tan(\beta)}.$$
Sugerencia.-Considera la igualdad:
$$tan\theta=\frac{sen\theta}{cos\theta}$$
- Determina si las siguientes funciones son pares, impares o ninguna de las opciones anteriores:
- $sen(\theta).$
- $cos(\theta).$
- Obtén la gráfica de las siguientes funciones:
- $f(x)=sen(x+\frac{\pi}{2}).$
- $f(x)=-2cos(x)+1.$
Entradas relacionadas
- Ir a: Cálculo Diferencial e Integral I
- Entrada anterior del curso: Cálculo Diferencial e Integral I: Funciones polinomiales y racionales. Análisis geométrico de funciones.
- Entrada siguiente del curso: Cálculo Diferencial e Integral I:Funciones trigonométricas (Segunda parte)
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»



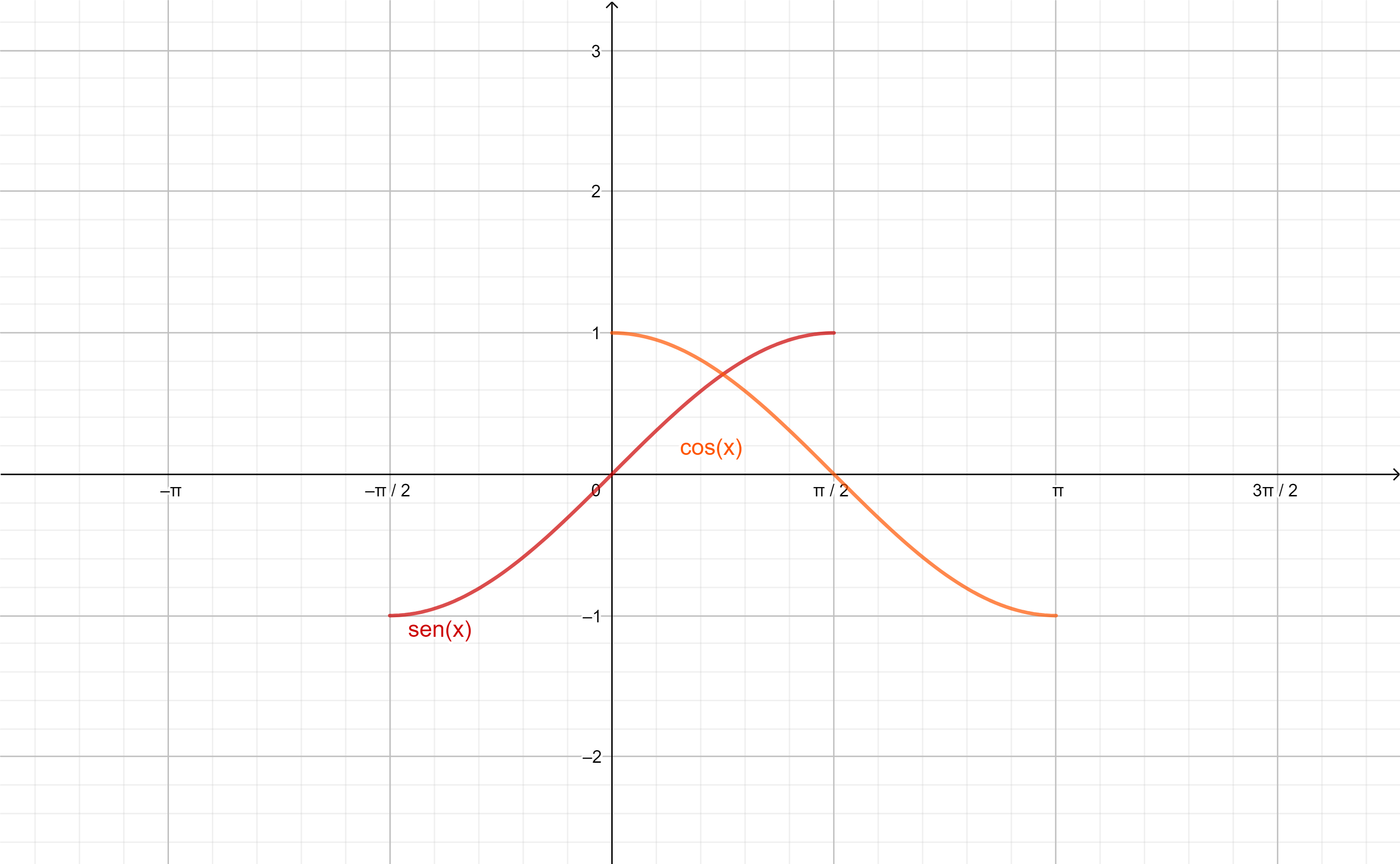
En la tarea moral en el denominador falta un «1» en la identidad de la tangente de la suma de ángulos.