Introducción

En esta entrada revisaremos el concepto de asíntota de una función; de manera intuitiva podemos pensar que mientras nos vamos «moviendo» a través de una curva, si ésta comienza a tener una distancia respecto a una recta cada vez más cercana a cero, entonces tal recta es una asíntota de la curva. En otras palabras, revisaremos aquellas curvas que a partir de determinado momento comienzan a tener un comportamiento muy similar al de una recta.

Un par de funciones conocidas

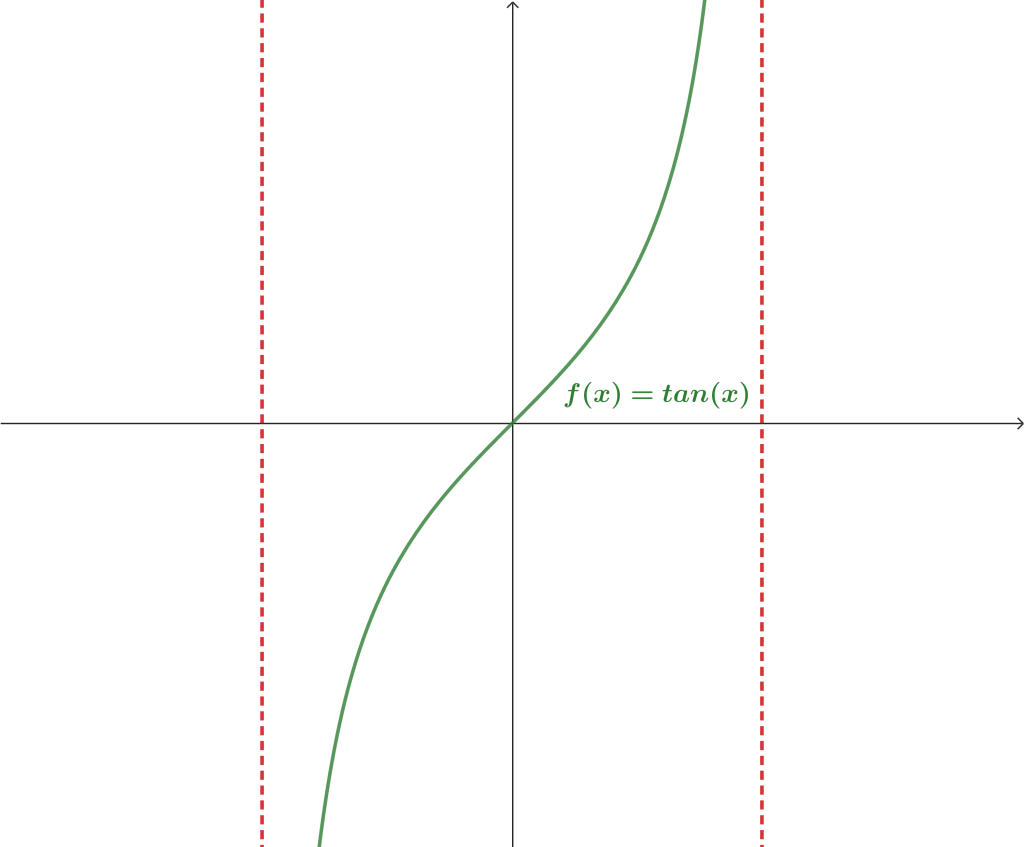
Daremos inicio a esta entrada retomando la función $f(x)=tan(x)$ estudiada en una entrada previa. Para nuestra revisión, consideraremos $f:(-\frac{\pi }{2},\frac{\pi }{2})\to \mathbb{R}$.

Recordemos que $f(x)=tan(x)=\frac{sen(x)}{cos(x)}$, notemos que la función tiene una particularidad cuando $x\to \frac{\pi }{2}$ y $x\to -\frac{\pi }{2}$, pues en estos puntos el denominador, $cos(x)$, se hace cero. Para investigar un poco más al respecto, veamos qué pasa en el límite.

$$\begin{array}{rl}\underset{x\to {\frac{\pi }{2}}^{-}}{lim}tan(x)=& \underset{x\to {\frac{\pi }{2}}^{-}}{lim}\frac{sen(x)}{cos(x)}\\ =& \mathrm{\infty }.\end{array}$$

Por otro lado,
$$\begin{array}{rl}\underset{x\to -{\frac{\pi }{2}}^{+}}{lim}tan(x)=& \underset{x\to -{\frac{\pi }{2}}^{+}}{lim}\frac{sen(x)}{cos(x)}\\ =& -\mathrm{\infty }.\end{array}$$

Con lo anterior, podemos notar que cuando nos acercamos por la izquierda a $\frac{\pi }{2}$, la función tiende a $\mathrm{\infty }$ y cuando nos acercamos por la derecha a $-\frac{\pi }{2}$ la función tiende a $-\mathrm{\infty }$, éstos son ejemplos de comportamiento asintótico y lo podemos visualizar con mayor facilidad en la siguiente gráfica:

Las rectas $l_1:x=-\frac{\pi }{2}$, $l_2:x=\frac{\pi }{2}$ (líneas punteadas en rojo) las llamaremos asíntotas de la función.

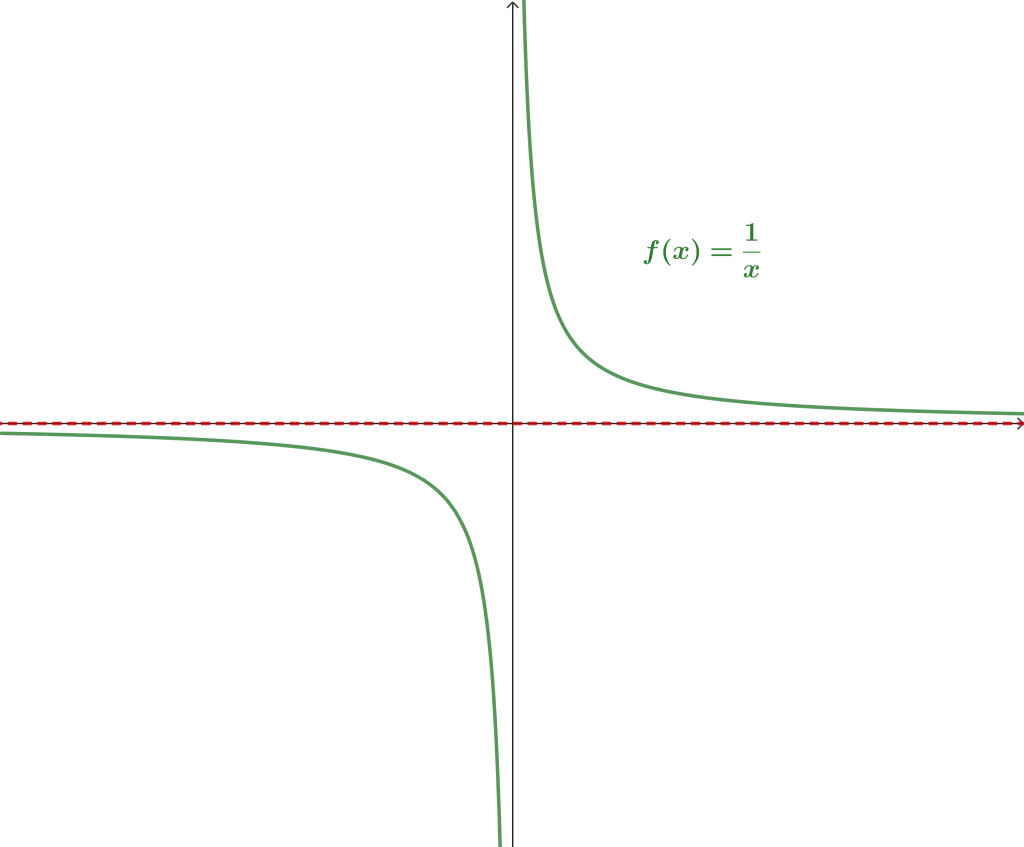
Revisemos un segundo ejemplo antes de dar las definiciones correspondientes. En una entrada anterior vimos que para la función $f(x)=\frac{1}{x}$, se tiene que $\underset{x\to \mathrm{\infty }}{lim}\frac{1}{x}=0$, análogamente se puede probar que $\underset{x\to -\mathrm{\infty }}{lim}\frac{1}{x}=0$. Tales límites nos indican que la función $f$ comienza a parecerse mucho a la recta $y=0$ cuando $x$ es muy grande o muy pequeño. En este sentido, dicha recta es una asíntota horizontal de $f$ tal y como lo podemos visualizar en la gráfica.

Tras haber visto la gráfica de la función es claro que también tiene un comportamiento similar al de una recta cuando $x\to 0$. Si bien el límite en tal punto no existe, ya conocemos sus límites laterales:

$$\underset{x\to 0^{+}}{lim}\frac{1}{x}=\mathrm{\infty },\underset{x\to 0^{-}}{lim}\frac{1}{x}=-\mathrm{\infty }.$$

Cuando sucede que el límite en un punto $x_0$ es $\mathrm{\infty }$ ó $-\mathrm{\infty }$, a la recta $x=x_0$ se le llama asíntota vertical. De esta manera, en nuestro ejemplo tenemos dos tipos de asíntotas: horizontal y vertical.

Existe un tercer tipo llamado asíntota oblicua que sucede cuando la función se aproxima a una recta del tipo $y=ax+b$ con $a\ne 0.$

Asíntota de una curva

A continuación presentamos la definición de los 3 tipos de asíntotas.

Definición (Asíntota vertical). Sea $x=x_0$ una recta $l$. Decimos que $l$ es asíntota vertical de la curva $f$ si se cumple al menos una de las siguientes condiciones:

1. $\underset{x\to x_0}{lim}f(x)=\pm \mathrm{\infty }.$
2. $\underset{x\to x_0^{-}}{lim}f(x)=\pm \mathrm{\infty }.$
3. $\underset{x\to x_0^{+}}{lim}f(x)=\pm \mathrm{\infty }.$

Notemos que las condiciones nos indican que una función tiene una asíntota vertical si mientras nos acercamos a determinado punto $x_0$ (ya sea por la izquierda, derecha o de ambas formas) la función crece o decrece de forma arbitraria. Este tipo de asíntotas suelen presentarse en las funciones racionales donde el denominador se hace cero.

Definición (Asíntota horizontal). Sea $y=b$ una recta $l$. Decimos que $l$ es una asíntota horizontal de la curva $f$ si se cumple al menos una de las siguientes condiciones:

1. $\underset{x\to \mathrm{\infty }}{lim}f(x)=L.$
2. $\underset{x\to -\mathrm{\infty }}{lim}f(x)=L.$

En este caso, la definición nos indica que existe una asíntota horizontal si la función comienza a acercarse a un número real conforme $x$ se hace arbitrariamente grande o pequeño.

Definición (Asíntota Oblicua). Sea $y=ax+b$ una recta $l$. Decimos que $l$ es una asíntota oblicua de la curva $f$ si se cumple alguna de las siguientes condiciones:

1. $\underset{x\to \mathrm{\infty }}{lim}[f(x)-(ax+b)]=0.$
2. $\underset{x\to -\mathrm{\infty }}{lim}[f(x)-(ax+b)]=0.$

La forma práctica de encontrar las asíntotas oblicuas de una curva $f$ es de la manera siguiente:

Si existen los límites $\underset{x\to \pm \mathrm{\infty }}{lim}\frac{f(x)}{x}=a$ y $\underset{x\to \pm \mathrm{\infty }}{lim}[f(x)-ax]=b.$

La recta $y=ax+b$ es una asíntota oblicua. Particularmente si $a=0$, esto se reduce al caso asíntota horizontal.

Ahora veremos algunos ejemplos donde encontraremos todas las asíntotas para cada función dada.

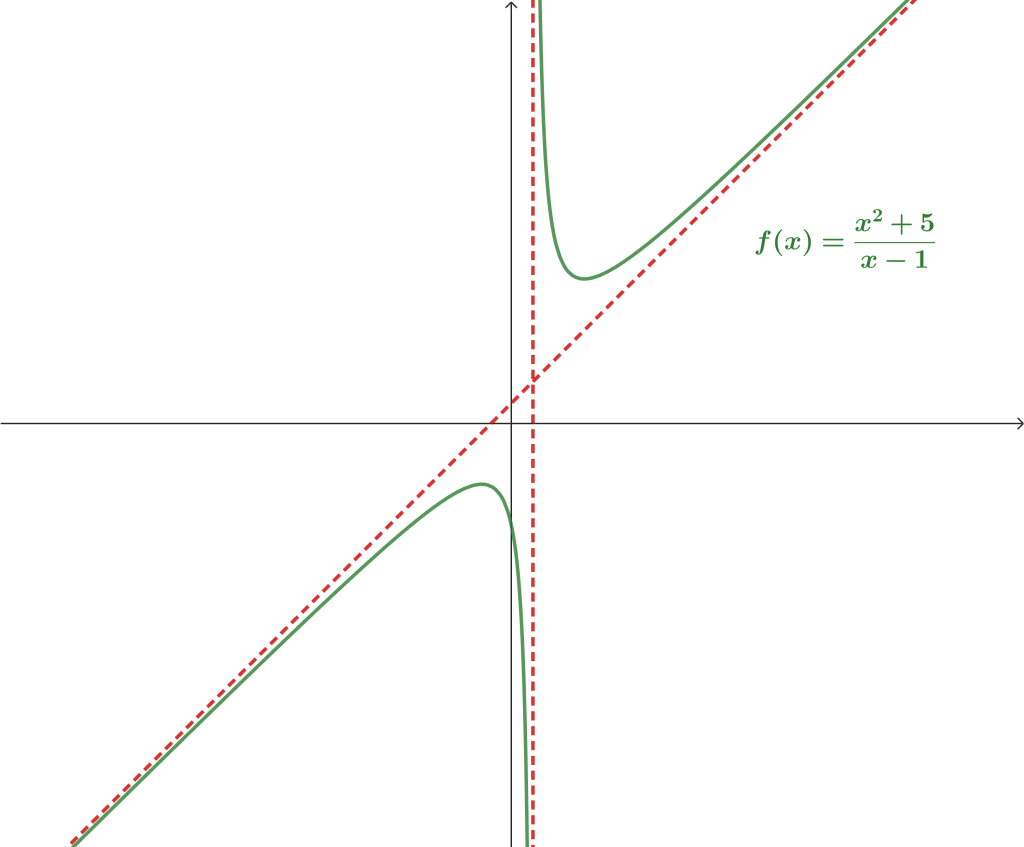
Ejemplo 1. Encuentra las asíntotas de la función $f(x)=\frac{x^2+5}{x-1}.$

• Asíntota vertical.
  Notemos que de la primera definición nos interesa encontrar los puntos en los cuales la función tiende a infinito o menos infinito, y el denominador se acerca a cero cuando $x\to 1$. Es decir $$\underset{x\to 1^{+}}{lim}\frac{x^2+5}{x-1}=\mathrm{\infty }\text{ y }\underset{x\to 1^{-}}{lim}\frac{x^2+5}{x-1}=-\mathrm{\infty }.$$
  Por lo tanto, $x=1$ es una asíntota vertical.
• Asíntota horizontal.
  $$\underset{x\to \mathrm{\infty }}{lim}\frac{x^2+5}{x-1}=\mathrm{\infty }\text{ y }\underset{x\to -\mathrm{\infty }}{lim}\frac{x^2+5}{x-1}=-\mathrm{\infty }.$$
  Por lo que no hay asíntotas horizontales.
• Asíntota oblicua.
  Veamos ahora que
  $$\begin{array}{rl}\underset{x\to \pm \mathrm{\infty }}{lim}\frac{f(x)}{x}=& \underset{x\to \pm \mathrm{\infty }}{lim}\frac{\frac{x^2+5}{x-1}}{x}\\ \\ =& \underset{x\to \pm \mathrm{\infty }}{lim}\frac{x^2+5}{x^2-x}\\ \\ =& \underset{x\to \pm \mathrm{\infty }}{lim}\frac{x^2+5}{x^2-x}\cdot \frac{\frac{1}{x^2}}{\frac{1}{x^2}}\\ \\ =& \underset{x\to \pm \mathrm{\infty }}{lim}\frac{1+\frac{5}{x^2}}{1-\frac{1}{x}}\\ \\ =& 1.\end{array}$$
  
  Por otro lado,
  $$\begin{array}{rl}\underset{x\to \pm \mathrm{\infty }}{lim}[f(x)-ax]=& \underset{x\to \pm \mathrm{\infty }}{lim}\frac{x^2+5}{x-1}-x\\ \\ =& \underset{x\to \pm \mathrm{\infty }}{lim}\frac{x^2+5-x^2+x}{x-1}\\ \\ =& \underset{x\to \pm \mathrm{\infty }}{lim}\frac{x+5}{x-1}\\ \\ =& 1.\end{array}$$
  Así, tenemos una asíntota oblicua en $y=x+1$.

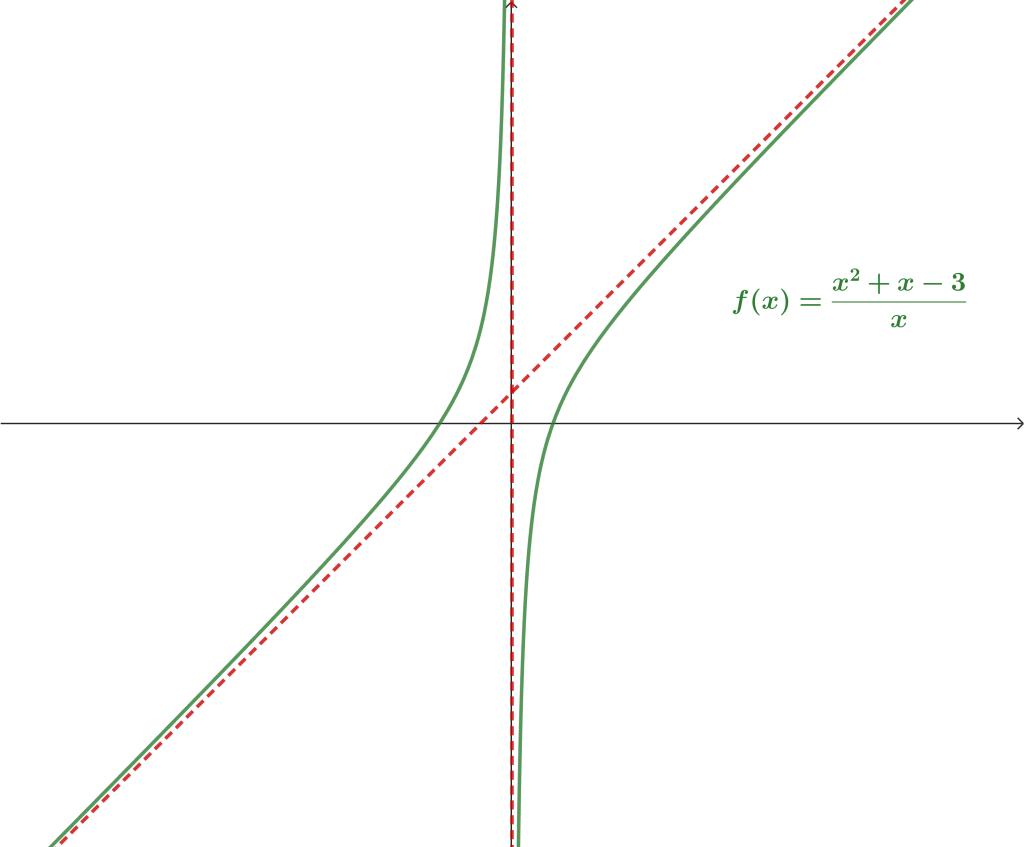
Ejemplo 2. $f(x)=\frac{x^2+x-3}{x}.$

• Asíntota vertical.
  Notemos que
  $$\underset{x\to 0^{+}}{lim}\frac{x^2+x-3}{x}=-\mathrm{\infty }\text{y}\underset{x\to 0^{-}}{lim}\frac{x^2+x-3}{x}=\mathrm{\infty }.$$
  Por lo tanto, hay una asíntota vertical en $x=0$.

• Asíntota horizontal.
  $$\underset{x\to \mathrm{\infty }}{lim}\frac{x^2+x-3}{x}=\mathrm{\infty }\text{y}\underset{x\to -\mathrm{\infty }}{lim}\frac{x^2+x-3}{x}=-\mathrm{\infty }.$$
  Por lo tanto, no hay asíntota horizontal.
• Asíntota Oblicua.
  $$\begin{array}{rl}\underset{x\to \pm \mathrm{\infty }}{lim}\frac{f(x)}{x}=& \underset{x\to \pm \mathrm{\infty }}{lim}\frac{\frac{x^2+x-3}{x}}{x}\\ \\ =& \underset{x\to \pm \mathrm{\infty }}{lim}\frac{x^2+x-3}{x^2}\\ \\ =& 1.\end{array}$$
  $$\begin{array}{rl}\underset{x\to \pm \mathrm{\infty }}{lim}[f(x)-ax]=& \underset{x\to \pm \mathrm{\infty }}{lim}\frac{x^2+x-3}{x}–x\\ \\ =& \underset{x\to \pm \mathrm{\infty }}{lim}\frac{x^2+x-3-x^2}{x}\\ \\ =& \underset{x\to \pm \mathrm{\infty }}{lim}\frac{x-3}{x}\\ \\ =& 1.\end{array}$$
  
  Así, $f$ tiene como asíntota oblicua la recta $y=x+1$.
  
  
  

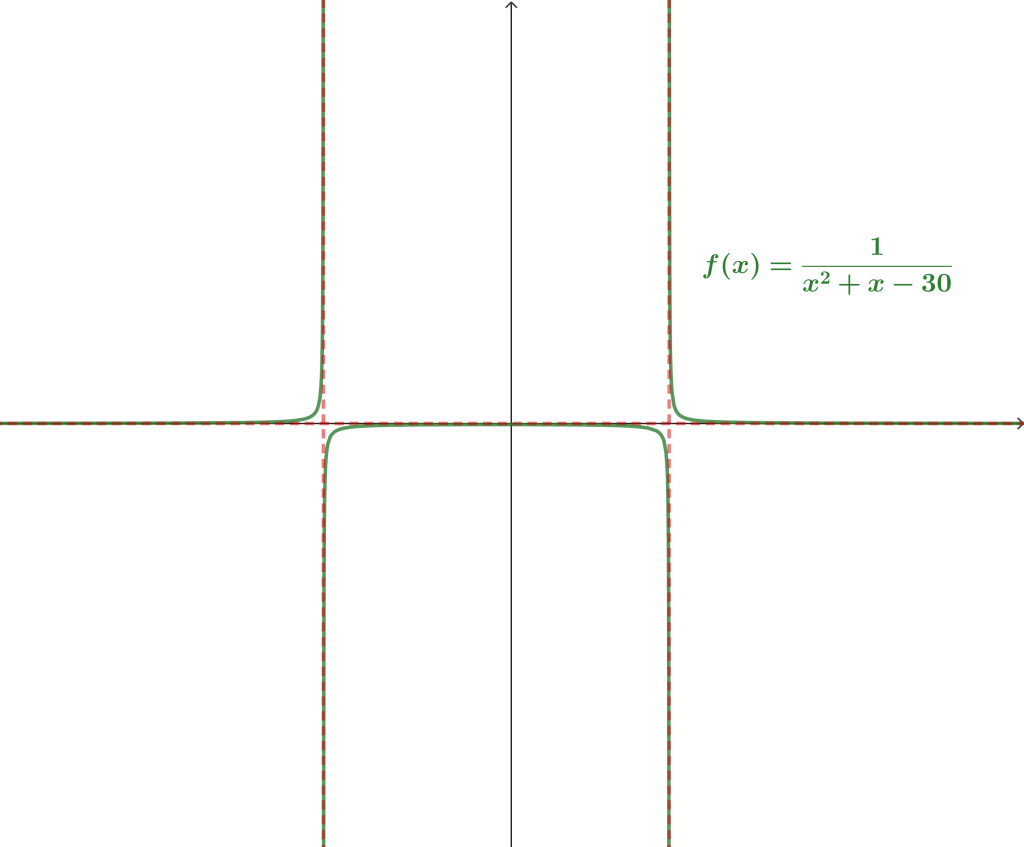
Ejemplo 3. $f(x)=\frac{1}{x^2+x-30}.$

• Asíntota vertical.
  Revisemos en qué momento el denominador se hace cero
  $x^2+x-30=0⟺(x+6)(x-5)=0⟺x=-6\text{ ó }x=5.$
  Así,
  $$\underset{x\to -6^{+}}{lim}\frac{1}{x^2+x-30}=-\mathrm{\infty }\text{y}\underset{x\to -6^{-}}{lim}\frac{1}{x^2+x-30}=\mathrm{\infty }.$$
  $$\underset{x\to 5^{+}}{lim}\frac{1}{x^2+x-30}=\mathrm{\infty }\text{y}\underset{x\to 5^{-}}{lim}\frac{1}{x^2+x-30}=-\mathrm{\infty }.$$
  Por tanto, hay dos asíntotas verticales, una en $x=5$ y otra en $x=-6$.
• Asíntota horizontal.
  $$\underset{x\to \pm \mathrm{\infty }}{lim}\frac{1}{x^2+x-30}=0$$
  Hay una asíntota horizontal en $y=0$.
• Asíntota oblicua.
  $$\begin{array}{rl}\underset{x\to \pm \mathrm{\infty }}{lim}\frac{f(x)}{x}=& \underset{x\to \pm \mathrm{\infty }}{lim}\frac{\frac{1}{x^2+x-30}}{x}\\ \\ =& \underset{x\to \pm \mathrm{\infty }}{lim}\frac{1}{x^3+x^2-30x}\\ \\ =& 0.\end{array}$$
  Como el límite es cero, no hay asíntota oblicua.

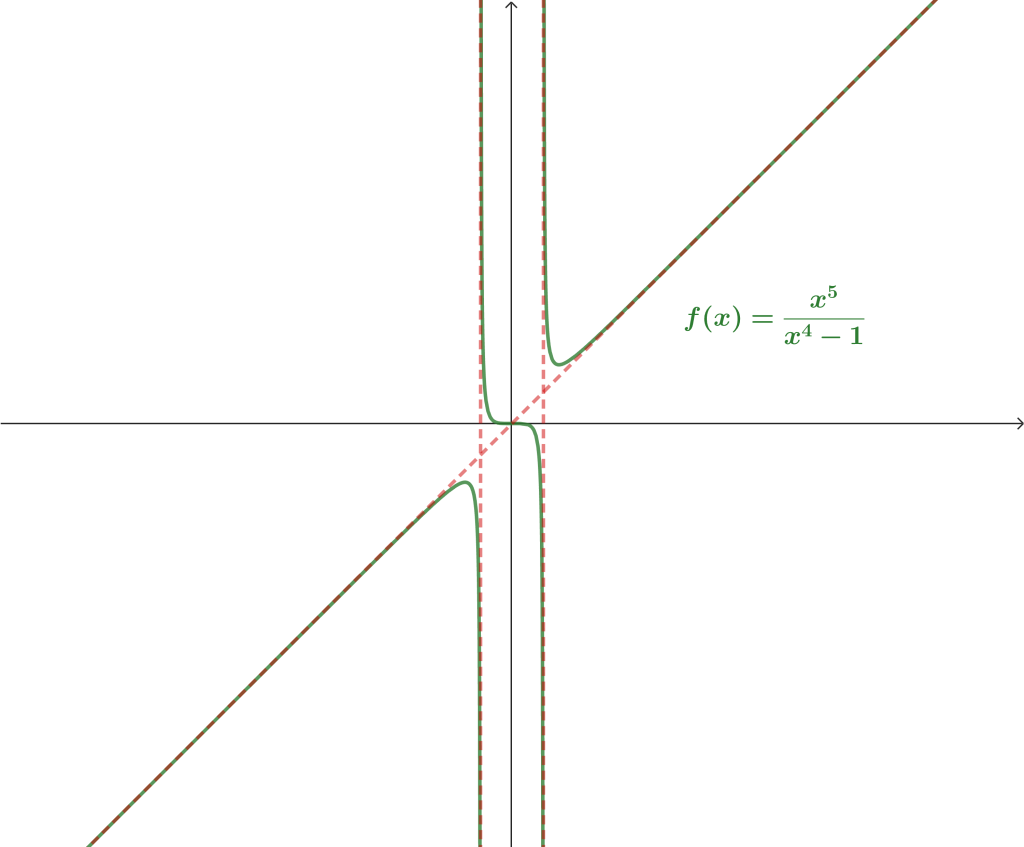
Ejemplo 4. $f(x)=\frac{x^5}{x^4-1}.$

• Asíntota vertical.
  El denominador se hace cero si $x^4–1=0⟺x=1\text{ ó }x=-1$
  $$\underset{x\to -1^{+}}{lim}\frac{x^5}{x^4-1}=\mathrm{\infty }\text{y}\underset{x\to -1^{-}}{lim}\frac{x^5}{x^4-1}=-\mathrm{\infty }$$
  $$\underset{x\to 1^{+}}{lim}\frac{x^5}{x^4-1}=\mathrm{\infty }\text{y}\underset{x\to 1^{-}}{lim}\frac{x^5}{x^4-1}=-\mathrm{\infty }$$
  Por lo tanto, hay dos asíntotas verticales, una en $x=1$ y otra en $x=-1$.
• Asíntota horizontal.
  Notemos que
  $$\underset{x\to \pm \mathrm{\infty }}{lim}\frac{x^5}{x^4-1}=\pm \mathrm{\infty }$$
  Por lo que no hay asíntota horizontal.
• Asíntota oblicua.
  $$\begin{array}{rl}\underset{x\to \pm \mathrm{\infty }}{lim}\frac{f(x)}{x}=& \underset{x\to \pm \mathrm{\infty }}{lim}\frac{\frac{x^5}{x^4-1}}{x}\\ \\ =& \underset{x\to \pm \mathrm{\infty }}{lim}\frac{x^5}{x^5-x}\\ \\ =& 1.\end{array}$$
  $$\begin{array}{rl}\underset{x\to \pm \mathrm{\infty }}{lim}[f(x)-ax]=& \underset{x\to \pm \mathrm{\infty }}{lim}\frac{x^5}{x^4-1}–x\\ \\ =& \underset{x\to \pm \mathrm{\infty }}{lim}\frac{x^5-x^5+x}{x^4-1}\\ \\ =& \underset{x\to \pm \mathrm{\infty }}{lim}\frac{x}{x^4-1}\\ \\ =& 0.\end{array}$$
  Así, $f$ tiene como asíntota oblicua la recta $y=x$.
  

Más adelante…

En las siguientes entradas estudiaremos el concepto de continuidad puntual y en un intervalo, también veremos diversos teoremas de las funciones continuas; para hacer la revisión de este nuevo concepto haremos amplio uso de la definición de límite, así como las propiedades que se revisaron a lo largo de esta unidad.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Encuentra todas las asíntotas de las siguientes funciones:

• $f(x)=\frac{x^2+2}{x+1}.$
• $f(x)=\frac{x^5+1}{x^2-1}.$
• $f(x)=x\sqrt{\frac{x+10}{x-10}}.$
• $f(x)=\frac{x^2+3}{\sqrt{x^2+4}}.$
• $f(x)=\frac{1-x^2}{x^2-4}.$

Entradas relacionadas

• Ir a Cálculo Diferencial e Integral I
• Entrada anterior del curso: Límites de funciones trigonométricas
• Siguiente entrada del curso: Definición de continuidad y sus propiedades
• Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»