Archivo del Autor: Miguel Ángel Rodríguez García

Cálculo Diferencial e Integral II: Introducción a funciones de varias variables

Por Miguel Ángel Rodríguez García

Deja un comentario

Introducción

Con esta sección acabamos el curso de Cálculo Diferencial e Integral II, por lo que daremos una breve introducción a funciones de varias variables ya que su siguiente curso de Cálculo Diferencial e Integral III se enfoca en varias variables. Comencemos definiendo una función en varias variables.

Funciones en varias variables

Definición: Una función $f:D\subset \mathbb{R}^{n}\mapsto \mathbb{R}^{m}$ es que a cada punto $X \space \epsilon \space D$ le corresponde un único punto $Y \space \epsilon \space \mathbb{R}^{n}$ lo cual se denota como $Y=f(X)$ y que llamaremos la imagen del punto $X$ mediante la función $f$.

Observemos que a $X$ se define como:

$$X=(x_{1}, x_{2}, x_{3}, …., x_{n})$$

y la función $f$:

$$f(X)=(f_{1}(x_{1}, x_{2}, …., x_{n}), f_{2}(x_{1}, x_{2}, …., x_{n}), …., f_{m}(x_{1}, x_{2}, …., x_{n}))$$

Donde cada $f_{i}$ con $i=1,….,m$ es la componente i-esima de la función $f$, asi:

$$f=(f_{1},…., f_{m})$$

Ejemplos

  • Sea $f:D\subset \mathbb{R}^{3}\mapsto \mathbb{R}^{2}$ definida como:

$$f(x,y,z)=(x^{2}+y^{2}+z^{2}, \frac{\sin(xy)}{x-y})$$

Donde $D={(x,y,z) \space\epsilon \space \mathbb{R}^{3}}$ con $\space x \neq y$. Las componentes de $f$ son:

$$f_{1}(x,y,z)=x^{2}+y^{2}+z^{2}\space \space \space \space \space \space \space f_{2}(x,y,z)=\frac{\sin(xy)}{x-y}$$

  • Sea $f:\mathbb{R}^{3}\mapsto \mathbb{R}^{3}$ definida como $f(x,y,z)=(x^{2}, y^{2}, x^{2}-z^{2})$ por lo que las componentes de $f$ son:

$$f_{1}(x,y,z)=x^{2}\space \space \space \space f_{2}(x,y,z)=y^{2} \space \space \space \space f_{3}(x,y,z)=x^{2}-z^{2}$$

El conjunto $\mathbb{R}^{n}$ tiene estructura de espacio vectorial si definimos las operaciones de suma y producto por escalares como sigue:

  • Dados $X=(x_{1}, …., x_{n}) \space \epsilon \space \mathbb{R}^{n}, Y=(y_{1}, ….., y_{n}) \space \epsilon \space \mathbb{R}^{n}$,

$$X+Y=(x_{1}, …., x_{n})+(y_{1}, …., y_{n})=(x_{1}+y_{1}, …., x_{n}+y_{n})$$.

  • Dados $X=(x_{1}, …., x_{n}) \space \epsilon \space \mathbb{R}^{n}, \lambda \space \epsilon \space \mathbb{R}^{n}$,

$$\lambda X=\lambda (x_{1}, …., x_{n})=(\lambda x_{1}, …., \lambda x_{n})$$.

Por eso mismo, a $X=(x_{1}, …., x_{n}) \space \epsilon \space \mathbb{R}^{n}$ se les denomina vectores.

Definición:

Si $m=1$ se dice que la función $f: D \subseteq \mathbb{R}^{n} \mapsto \mathbb{R}$ es una función real o campo escalar de n-variables.

Si $m>1$ se dice que la función $f: D \subseteq \mathbb{R}^{n} \mapsto \mathbb{R}^{m}$ es una función vectorial o un campo vectorial de n-variables y m-componentes.

Veamos la definición de una grafica en varias variables.

Definición: Sea $f: D \subset \mathbb{R}^{n} \mapsto \mathbb{R}$. Se define la gráfica de la función $f$ como:

$$Gr(f)={(x_{1}, …., x_{n},y) \space \epsilon \space \mathbb{R}^{n+1}: (x_{1}, …., x_{n}) \space \epsilon \space D, y=f(x_{1}, …., x_{n}) }$$

Cuando $n=1$ la representación de $f$ nos proporciona una curva en $\mathbb{R}^{2}$, en el caso cuando $n=2$ nos proporciona una superficie en $\mathbb{R}^{3}$.

Curvas de nivel

En general, para una función de dos variables no es facil graficarla por lo que tenemos que recurrir a otras tecnicas para graficar estas funciones, una tecnica se le conoce como curvas de nivel el cual consiste en que la función se igual a una constante.

$$f(x,y)=k$$

Donde $k$ es una constante.

Gráficamente lo que se esta haciendo es que a la grafica de la función $f(x,y)$ la estamos cortando en «rebanadas» para cada valor de $k$ distinta por lo que veremos para cada corte, una parte de la grafica de la función $f(x,y)$.

Veamos el siguiente ejemplo.

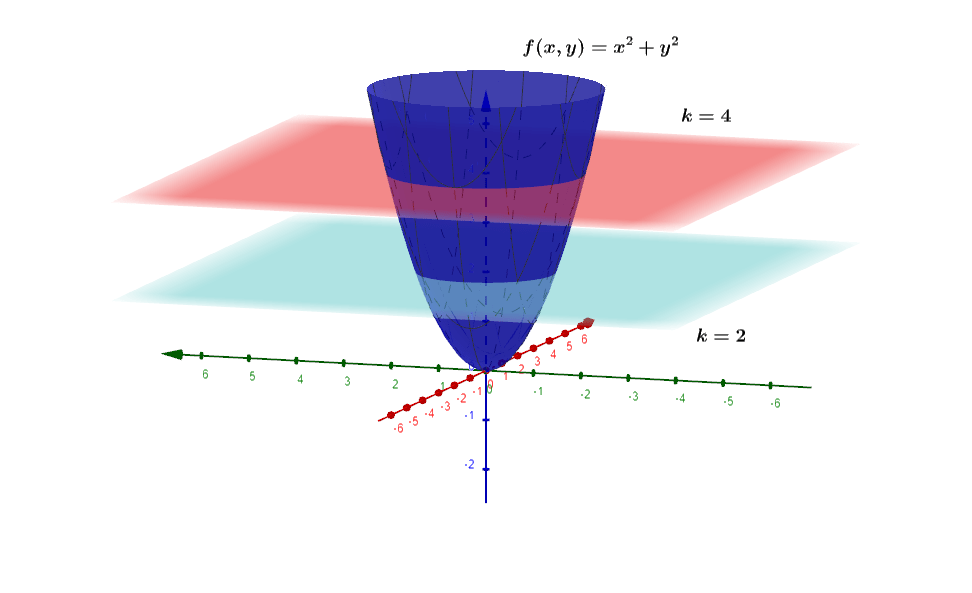
Figura 1: Función $f(x,y)$ cortada por dos planos.

De la figura $(1)$ tenemos la función de dos variables $f(x,y)=x^{2}+y^{2}$ que es el cono azul de la figura $1$, si le hacemos unos cortes por dos planos con valores $k=2$ y $k=4$ obtendremos que las curvas de nivel (viéndolos desde la perspectiva de arriba) se notan como circunferencias como se muestran en la figura $(2)$.

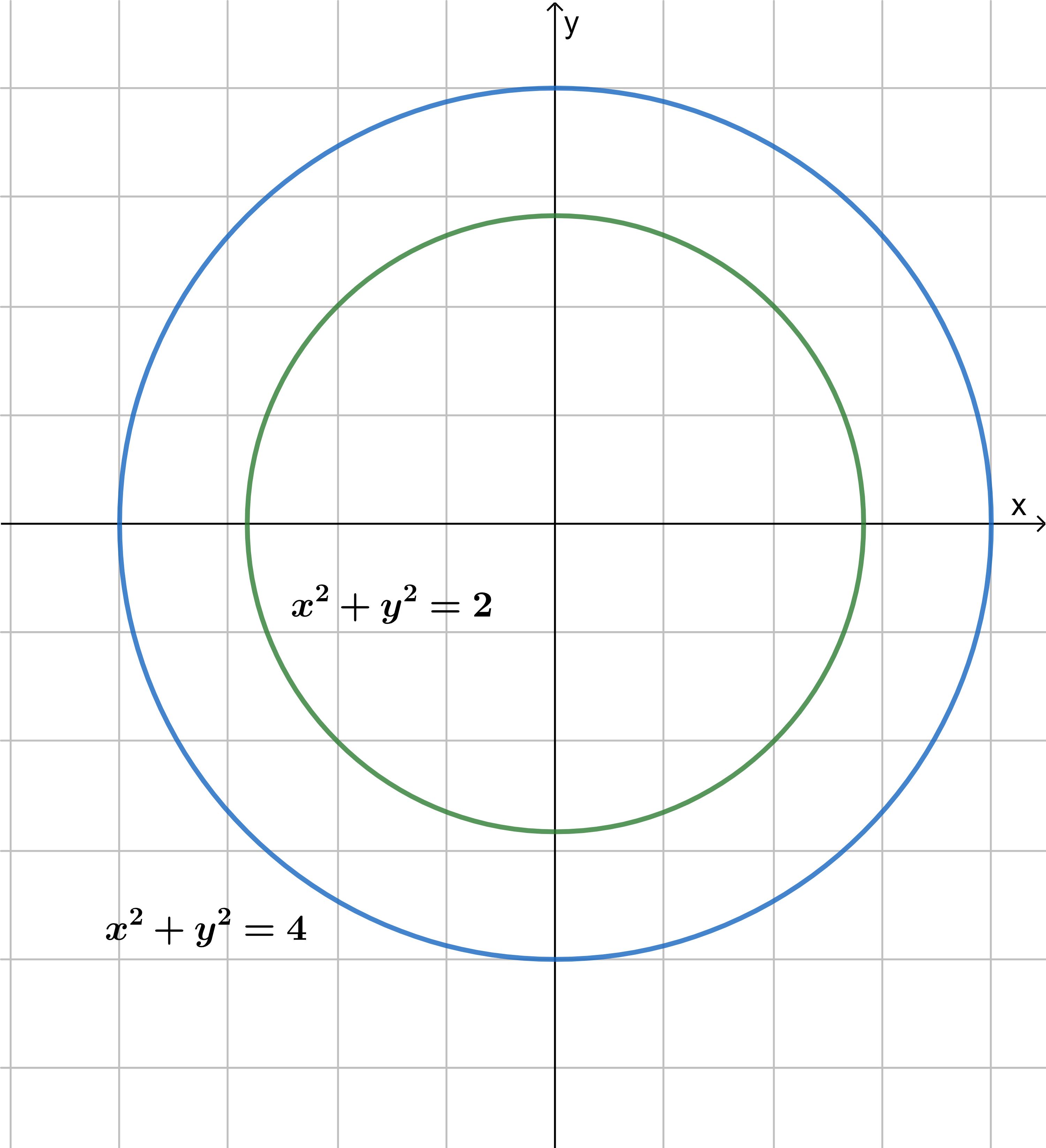
Figura 2: Curvas de nivel para los valores $k=2$ y $k=4$ a la función $f(x,y)$.

Análogamente a este método de graficar funciones de dos variables, para tres variables se puede hacer lo mismo el cual se le conoce como el método de curvas de superficies.

Otro concepto importante para esta introducción a varias variables es la topología, lo que es usual en una variable el concepto de una función dentro de un intervalo abierto, cerrado, propio o impropio, se extiende estos concepto para funciones de varias variables. Como esta sección es una pequeña introducción a funciones de varias variables no se verán estos conceptos pero si se recomienda tener un poco de noción de estos conceptos de topología.

Tarea moral

Los siguientes ejercicios no son para evaluación pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionado con el tema visto.

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Encuentra el dominio y el rango de la función $f(x,y)=\sqrt{9-x^{2}-y^{2}}$
  2. Sea la función $f(x,y)=x^{2}+3y^{2}$, hallas las curva de nivel con $k=1,2 \space y \space 3$
  3. Obtén la grafica de la función $z=x^{2}-y^{2}$
  4. Hallar las superficies de nivel de la función $f(x,y,z)=x^{2}+y^{2}-z^{2}$ con $k=0$ y $k=-1$

Más adelante…

En esta entrada vimos una introducción a las funciones de varias variables como paso para estudiar estas funciones de varias variables con mas detenimiento en el curso de Cálculo Diferencial e Integral III, así como se estudio las funciones de una variable.

Con esta entrada concluimos el curso de Cálculo Diferencial e Integral II.

Entradas relacionadas

Cálculo Diferencial e Integral II: Funciones hiperbólicas

Por Miguel Ángel Rodríguez García

Deja un comentario

Introducción

En esta sección veremos unas funciones cuyas definiciones se basan en la función exponencial, a estas funciones se les conoce como funciones hiperbólicas, el nombre de hipérbolas se basa en que estas funciones cumplen la relación con la hipérbola:

$$x^{2}-y^{2}=1 \tag{1}$$

Funciones hiperbólicas

Recordemos que la relación $(1)$ es la ecuación de una hipérbola equilátera, por lo cual las asíntotas son perpendiculares. Definimos las funciones de seno hiperbólico y coseno hiperbólico como:

$$\sinh(x)=\frac{e^{x}-e^{-x}}{2} \tag{2}$$

$$\cosh(x)=\frac{e^{x}+e^{-x}}{2} \tag{3}$$

De estas dos funciones podemos definir las siguientes funciones:

$$\tanh(x)=\frac{\sinh(x)}{\cosh(x)}$$

$$\coth(x)=\frac{\cosh(x)}{\sinh(x)}$$

$$sech(x)=\frac{1}{\cosh(x)}$$

$$csch(x)=\frac{1}{\sinh(x)}$$

Notemos que estas funciones hiperbólicas llevan el nombre de las funciones trigonométricas y es que estas funciones trigonométricas tienen características similares a las funciones trigonométricas.

Veamos que las funciones hiperbólicas $\sinh(x)$ y $\cosh(x)$ cumplen la relación de una hiperbóla dada por la relación $(1)$:

$$\cosh^{2}(x)-\sinh^{2}(x)=\left ( \frac{e^{x}+e^{-x}}{2} \right )^{2}-\left ( \frac{e^{x}-e^{-x}}{2} \right )^{2}$$

$$=\frac{e^{2x}+2e^{x}e^{-x}+e^{-2x}}{4}+\frac{-e^{2x}+2e^{x}e^{-x}-e^{-2x}}{4}=\frac{2+2}{4}=1$$

$\space$

Figura 1: Grafica de las funciones $\sinh(x)$ y $\cosh(x)$.

La función seno hiperbólico también cumple con ser una función impar, veamos:

$$\sinh(-x)=\frac{e^{-x}-e^{-(-x)}}{2}=\frac{e^{-x}-e^{x}}{2}=-\frac{e^{x}-e^{-x}}{2}=-\sinh(x)$$

Análogamente, se puede demostrar que las siguientes funciones son funciones impares: $\coth(x)$ y $csch(x)$, y las siguientes funciones son pares: $\cosh(x)$, $\tanh(x)$ y $sech(x)$.

Algunas relaciones importantes de estas funciones son las siguientes:

  • $$e^{x}=\cosh(x)+\sinh(x)$$
  • $$e^{-x}=\cosh(x)-\sinh(x)$$

Es fácil demostrar las relaciones anteriores por definición $(2)$ y $(3)$.

Otra propiedad es la siguiente:

  • $$\sinh(x\pm y)=\sinh(x)\cosh(y)\pm \cosh(x)\sinh(y)$$

Demostración:

Por definición, tenemos que:

$$\sinh(x\pm y)=\frac{e^{x\pm y}-e^{-x\mp y}}{2}=\frac{e^{x}e^{\pm y}-e^{-x}e^{\mp y}}{2}$$

Por las relaciones anteriores se tiene que:

$$\frac{e^{x}e^{\pm y}-e^{-x}e^{\mp y}}{2} =\frac{(\cosh(x)+\sinh(x))(\cosh( y)\pm \sinh(y))-(\cosh(x)-\sinh(x))(\cosh(y)\mp \sinh(y))}{2}=$$

$$\frac{\cosh(x)\cosh(y)\pm \cosh(x)\sinh(y)+\sinh(x)\cosh(y)\pm \sinh(x)\sinh(y)-\cosh(x)\cosh(y)\pm \cosh(x)\sinh( y)}{2}$$

$$\frac{+(\sinh(x)\cosh(y)\mp \sinh(x)\sinh( y)}{2}$$

Dependiendo del signo, lo podemos reescribir como:

$$=\frac{2\sinh(x)\cosh( y)\pm 2\cosh(x)\sinh(y)}{2}=\sinh(x)\cosh(y)\pm \cosh(x)\sinh( y)$$

$\square$

La propiedad para la función $\cosh(x)$ viene dada como:

  • $$\cosh(x\pm y)=\cosh(x)\cosh(x)\pm \sinh(x)\sinh(x)$$

De las relaciones anteriores se puede demostrar que:

  • $$\cosh(2x)=\cosh^{2}(x)+\sinh^{2}(x)$$
  • $$sinh(2x)=2\cosh(x)+\sinh(x)$$

La derivación e integración de estas funciones es sencillo, veamos la siguiente tabla:

$$\frac{d}{dx}\sinh(x)=\cosh(x)$$
$$\frac{d}{dx}\cosh(x)=\sinh(x)$$
$$\frac{d}{dx}\tanh(x)=sech(x)$$
$$\frac{d}{dx}\coth(x)=csch(x)$$
$$\frac{d}{dx}sech(x)=-sech(x)\tanh(x)$$
$$\frac{d}{dx}csch(x)=-csch(x)\coth(x)$$
Tabla 1: Derivada de las funciones hiperbólicas.

Notemos que las derivadas son similares a las derivadas de las funciones trigonométricas, al ser la derivada una función inversa de la integral entonces las integrales son similares a las funciones trigonométricas, veamos la siguiente tabla:

$$\int \sinh(x)=\cosh(x)+c$$
$$\int \cosh(x)=\sinh(x)+c$$
$$\int \tanh(x)=log(\cosh(x))+c$$
$$\int \coth(x)=log(\sinh(x))+c$$
$$\int sech(x)=2\tan^{-1}\left ( \tanh(\frac{x}{2}) \right )+c$$
$$\int csch(x)=log\left ( \tanh(\frac{x}{2}) \right )$$
Tabla 2: Integrales de las funciones hiperbólicas.

Funciones hiperbólicas inversas

Análogamente a las funciones trigonométricas, se definen las funciones hiperbólicas inversas como:

  1. $$\sinh^{-1}(x)=arcsinh(x)=ln\left ( x+\sqrt{x^{2}+1} \right )$$
  2. $$\cosh^{-1}(x)=arccosh(x)=ln\left ( x+\sqrt{x^{2}-1} \right )$$
  3. $$\tanh^{-1}(x)=arctanh(x)=\frac{1}{2}ln\left ( \frac{1+x}{1-x} \right )$$
  4. $$\coth^{-1}(x)=arccoth(x)=\frac{1}{2}ln\left ( \frac{x+1}{x-1} \right )$$
  5. $$sech^{-1}(x)=arcsech(x)=ln\left ( \frac{1+\sqrt{1-x^{2}}}{x} \right )$$
  6. $$csch^{-1}(x)=arccsch(x)=ln\left ( \frac{1}{x}+\sqrt{\frac{1}{x^{2}}+1} \right )$$

La demostración para la función hiperbólica inversa den $\sinh(x)$ es como sigue:

Sea $y=arcsinh(x) \Rightarrow \sinh(y)=x$

Utilizamos la relación $(1)$, por lo que:

$$\cosh^{2}(y)=1+\sinh^{2}(y)=1+x^{2}$$

$$\Rightarrow \cosh(y)=\sqrt{1+x^{2}}$$

Sumando en ambos lados de la igualdad para obtener la exponencial, se tiene que:

$$e^{y}=\cosh(y)+\sinh(y)=\sqrt{1+x^{2}}+x$$

$$y=arcsinh(x)=ln\left ( \sqrt{1+x^{2}}+x \right )$$

$\square$

La idea para las demostrar las demás funciones hiperbólicas inversas es la misma.

Tarea moral

Los siguientes ejercicios no son para evaluación pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionado con el tema visto.

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Demuestre la siguiente identidad: $\tanh^{2}(x)+sech^{2}(x)=1$.
  2. Demuestre que la función hiperbólica $\cosh(x)$ es una función impar.
  3. Demuestre que $\cosh(x\pm y)=\cosh(x)\cosh(x)\pm \sinh(x)\sinh(x)$.
  4. Demuestre que $\frac{d}{dx}csch(x)=-csch(x)\coth(x)$.
  5. Demuestre que $\int \tanh(x)=log(\cosh(x))+c$.

Más adelante…

En esta sección vimos las funciones hiperbólicas que cumplen con la ecuación de una hipérbola equilátera, así como, algunas propiedades tales como sus derivadas e integrales, también vimos que algunas de las propiedades de estas funciones son similares a las funciones trigonométricas, en la siguiente sección veremos una introducción a varias variables.

Entradas relacionadas

Cálculo Diferencial e Integral II: Longitud de arco en coordenadas polares

Por Miguel Ángel Rodríguez García

Deja un comentario

Introducción

En la sección anterior vimos como calcular el área de una curva que está acotada por una curva y el área entre dos curvas en coordenadas polares, en esta sección veremos como calcular la longitud de arco de una curva en coordenadas polares, la idea de calcular de la longitud es la misma para calcular la longitud de una curva en coordenadas cartesianas, en esta ocasión, lo haremos en coordenadas polares, pero para esto veamos un teorema para la longitud de arco para las curvas paramétricas.

Longitud de arco para curvas paramétricas

Teorema. Si una curva $C$ se describe mediante las ecuaciones paramétricas $x=f(t)$ y $y=g(t)$, con $\alpha \leq t \leq \beta$, donde $f’$ y $g’$ son continuas en el intervalo $[\alpha, \beta]$, entonces la longitud de $C$ que es recorrida una sola vez cuando $t$ aumenta desde $\alpha$ hasta $\beta$, se calcula como:

$$L=\int_{\alpha}^{\beta} \sqrt{\left ( \frac{dx}{dt} \right )^{2}+\left ( \frac{dy}{dt}\right )^{2}}dt$$

Demostración:

Sea $C$ la curva en un intervalo $[\alpha, \beta]$, se divide este intervalo en $n$ subintervalos $t_{0}, \space t_{1},…., \space t_{n}$ con longitud $\Delta t$. Aproximamos la curva $C$ con polígonos con vértices $P_{0}, \space, P_{1}, \space, …., P_{n}$, como se muestra en la figura $(1)$.

Figura 1: Aproximación de polígonos (líneas negras) a una curva $C$ (curva roja).

Si el número de polígonos tiende a infinito, es decir, $n \to \infty$, entonces:

$$L=\lim_{n \to \infty} \sum_{i=1}^{n}|P_{i-1}-P_{i}|$$

Aplicamos el teorema de valor medio a $f$ en el intervalo $[t_{i-1},t_{i}]$, encontramos un número $t^{*}_{i}$ tal que:

$$f(t_{i})-f(t_{i-1})=f'(t^{*}_{i})(t_{i}-t_{i-1})$$

Lo podemos reescribir en términos de deltas como:

$$\Delta x_{i}=f'(t^{*}_{i})\Delta t$$

Análogamente, hacemos lo mismo para $g(t)$, aplicando el teorema del valor medio encontrando un número $t^{**}_{i}$ tal que:

$$\Delta y_{i}=g'(t^{**}_{i})\Delta t$$

Por lo que la longitud la podemos escribir como:

$$L= \lim_{n \to \infty }\sum_{i=1}^{n} |P_{i-1}-P_{i}|=\lim_{n \to \infty }\sum_{i=1}^{n} \sqrt{(\Delta x)^{2}+(\Delta y)^{2}}$$

$$=\lim_{n \to \infty }\sum_{i=1}^{n}\sqrt{(f'(t^{*}_{i})\Delta t)^{2}+(g'(t^{**}_{i})\Delta t)^{2}}=\lim_{n \to \infty }\sum_{i=1}^{n}\sqrt{(f'(t^{*}_{i}))^{2}+(g'(t^{**}_{i}))^{2}}\Delta t$$

Si $f’$ y $g’$ son continuas, entonces el límite de la suma es el mismo que si $t^{*}_{i}$ y $t^{**}_{i}$ fueran iguales, por lo que:

$$L=\int_{\alpha}^{\beta}\sqrt{\left [ f'(t) \right ]^{2}+\left [ g'(t) \right ]^{2}}dt$$

En notación de Leibniz tenemos que:

$$L=\int_{\alpha}^{\beta} \sqrt{\left ( \frac{dx}{dt} \right )^{2}+\left ( \frac{dy}{dt}\right )^{2}}dt \tag{1}$$

$\square$

Este teorema nos servirá para calcular la longitud de una curva en coordenadas polares.

Longitud de arco en coordenadas polares

Sea una curva polar dada por $r=f(\theta)$, en un intervalo $a \leq \theta \leq b$, podemos escribir las ecuaciones paramétricas como:

$$x=r\cos(\theta)=f(\theta)\cos(\theta) \hspace{2cm} y=r\sin(\theta)=f(\theta)\sin(\theta)$$

Derivamos respecto a $\theta$ las dos anteriores ecuaciones, por lo que:

$$\frac{dx}{d\theta}=\frac{dr}{d\theta}\cos(\theta)-r\sin(\theta) \hspace{2cm} \frac{dy}{d\theta}=\frac{dr}{d\theta}\sin(\theta)+r\cos(\theta)$$

Elevando al cuadrado, y sumando las derivadas, obtenemos:

$$\left ( \frac{dx}{d\theta} \right )^{2}+\left ( \frac{dy}{d\theta} \right )^{2}=\left (\frac{dr}{d\theta}\cos(\theta)-r\sin(\theta) \right )^{2}+\left (\frac{dr}{d\theta}\sin(\theta)+r\cos(\theta) \right )^{2}$$

$$=\left (\frac{dr}{d\theta}\right )^{2}\cos^{2}(\theta)-2\frac{dr}{d\theta}\cos(\theta)r\sin(\theta)+r^{2}\sin^{2}(\theta)+\left (\frac{dr}{d\theta}\right )^{2}\sin^{2}(\theta)+2\frac{dr}{d\theta}\sin(\theta)r\cos(\theta)+r^{2}\cos^{2}(\theta)$$

Utilizando que $\sin^{2}(\theta)+\cos^{2}(\theta)=1$, entonces:

$$\left ( \frac{dx}{d\theta} \right )^{2}+\left ( \frac{dy}{d\theta} \right )^{2}=\left (\frac{dr}{d\theta}\right )^{2}+r^{2}$$

Utilizando la relación $(1)$, suponiendo que $f’$ es continua, entonces la longitud de una curva polar está dada como:

$$L=\int_{a}^{b} \sqrt{ r^{2}+\left ( \frac{dr}{d\theta}\right )^{2}}d\theta$$

Ejemplo

  • Encontrar la longitud del cardioide dado como: $r=1-\cos(\theta)$

En este caso, tenemos que:

$$r^{2}+\left ( \frac{dr}{d\theta}\right )^{2}=(1-\cos(\theta))^{2}+\sin^{2}(\theta)=1-2\cos(\theta)+\cos^{2}(\theta)+\sin^{2}(\theta)=2-2\cos(\theta)$$

Así la longitud de arco es:

$$L=\int_{0}^{2\pi} \sqrt{2-2\cos(\theta)}d\theta=\int_{0}^{2\pi} \sqrt{4\sin^{2}(\frac{\theta}{2})}d\theta=\int_{0}^{2\pi} \sqrt{4\sin^{2}(\frac{\theta}{2})}d\theta$$

$$=2\int_{0}^{2\pi}\sin(\frac{\theta}{2})d\theta=\left [ -4\cos(\frac{\theta}{2}) \right ]\bigg|^{2\pi}_{0}=4+4=8$$

Tarea moral

Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Encuentre la longitud de la curva polar dada como $r=3\sin(\theta)$, $0 \leq \theta \leq \frac{\pi}{3}$.
  2. Encuentre la longitud de la curva polar dada como $r=e^{2\theta)$, $0 \leq \theta \leq 2\pi$.
  3. Encuentre la longitud de la curva polar dada como $r=\theta^{2}$, $0 \leq \theta \leq 2\pi$.
  4. Encuentre la longitud de la curva polar de un pétalo de rosa dada como $r=\cos(2\theta)$.
  5. Encuentre la longitud de la curva polar de un cardiode dado como $r=a(1+\cos(\theta))$, $a > 0$.

Más adelante…

En esta sección vimos un teorema que nos dice como calcular la longitud de una curva dada por dos curvas paramétricas en general, aplicando este teorema, vimos que se puede utilizar para poder calcular la longitud de una curva en coordenadas polares. En la siguiente sección veremos las funciones hiperbólicas.

Entradas relacionadas

Cálculo Diferencial e Integral II: Área en coordenadas polares

Por Miguel Ángel Rodríguez García

Deja un comentario

Introducción

En la sección anterior vimos una introducción a las coordenadas polares, ahora veremos como calcular el área de una región acotada por una curva polar.

Área en coordenadas polares

Figura 1: Aproximación al área de la curva dada por $r=f(\theta)$.

Sea la curva polar $r=f(\theta)$ y los rayos $\theta=a$ y $\theta=b$ como se muestra en la figura $(1)$, con $f$ una función positiva y $0 < b-a \leq 2\pi$. Dividimos el intervalo $[a, b]$ en $n$ subintervalos $[\theta_{i-1}, \theta_{i}]$ con amplitud $\Delta \theta$, sea $\theta^{*}_{n}$ un punto medio en el intervalo $[\theta_{i-1}, \theta_{i}]$, entonces el área $\Delta A_{i}$ se aproxima al área de un circulo con un ángulo $\Delta \theta$ y radio $f(\theta^{*}_{n})$, recordando que el área del sector de un circulo es proporcional a su ángulo central:

$$A=\frac{\theta}{2\pi}\pi r^{2}=\frac{1}{2}r^{2}\theta$$

Entonces tenemos que:

$$\Delta A_{i}\approx \frac{1}{2}[f(\theta^{*}_{n})]^{2}\Delta \theta $$

Si sumamos todos los $n$ subintervalos, se tiene que:

$$\sum_{i=1}^{n}\Delta A_{i}\approx \sum_{i=1}^{n} \frac{1}{2}[f(\theta^{*}_{n})]^{2}\Delta \theta $$

Si hacemos tender $n \to \infty$, entonces:

$$\lim_{n \to \infty} \sum_{i=1}^{n} \frac{1}{2}[f(\theta^{*}_{n})]^{2}\Delta \theta=\int_{a}^{b} \frac{1}{2}[f(\theta^{*}_{n})]^{2} d \theta$$

Por tanto, el área para calcular la región acotada por la curva $r=f(\theta)$ y los rayos $\theta=a$ y $\theta=b$ esta dado como:

$$A=\int_{a}^{b} \frac{1}{2}[f(\theta^{*}_{n})]^{2} d \theta \tag{1}$$

A menudo, la ecuación $(1)$ se expresa como:

$$A=\int_{a}^{b} \frac{1}{2}r^{2} d \theta $$

Ejemplos

  • Determine el área encerrada por un bucle de la rosa de cuatro hojas cuya curva esta dada como: $r=\cos(2\theta)$.
Figura 2: Grafica de la curva $r=\cos(2\theta)$.

Como queremos solo un bucle, de la figura $(2)$, vemos que los rayos $\theta=\frac{\pi}{4}$ y $\theta=-\frac{\pi}{4}$ encierran el bucle derecho de la rosa, por lo que el área la calculamos como:

$$A=\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}}\frac{1}{2}r^{2}d\theta=\frac{1}{2}\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}}(\cos(2\theta))^{2}d\theta=\int_{0}^{\frac{\pi}{4}}(\cos(2\theta))^{2}d\theta$$

Utilizamos una relación para el coseno:

$$\cos^{2}(2x)=\frac{1}{2}(1+\frac{1}{4}\cos(4x))$$

Por ende:

$$A=\int_{0}^{\frac{\pi}{4}}(\cos(2\theta))^{2}d\theta=\int_{0}^{\frac{\pi}{4}}\frac{1}{2}(1+\cos(4\theta))d\theta=\frac{1}{2}\left [ \theta+\frac{1}{4}\sin(4\theta) \right ]\bigg|_{0}^{\frac{\pi}{4}}=\frac{\pi}{8}$$

Por tanto el área de un bucle de la rosa es: $A=\frac{\pi}{8}$

  • Determinar el área de la región en el plano, acotada por la cardioide $r=2(1+\cos(\theta))$.
Figura 3: Grafica de la curva $r=2(\cos(\theta)+1)$.

Como queremos toda el área del cardioide entonces integramos de $0$ a $2\pi$, por lo que:

$$A=\int_{0}^{2\pi} \frac{1}{2}r^{2}d\theta=\int_{0}^{2\pi} \frac{1}{2}4(1+\cos(\theta))^{2}d\theta=\int_{0}^{2\pi}2(1+2\cos(\theta)+\cos^{2}(\theta))d\theta$$

Utilizamos la relación:

$$\cos^{2}(x)=\frac{1+\cos(2x)}{2}$$

Por tanto:

$$\int_{0}^{2\pi} (2+4\cos(\theta)+1+\cos(2\theta)d\theta=\int_{0}^{2\pi} (3+4\cos(\theta)+\cos(2\theta)d\theta=\left [ 3\theta+4\sin(\theta)+\frac{\sin(2\theta)}{2} \right ]\bigg|_{0}^{2\pi}=6\pi$$

$\space$

El área entre dos curvas acotadas por las curvas $r_{1}=f(\theta)$ y $r_{2}=f(\theta)$, $(\theta)=a$ y $(\theta)=b$, con $f(\theta) \geq g(\theta) \geq 0$ y $0 < b-a \leq 2\pi$ se puede calcular mediante la siguiente formula:

$$\int_{a}^{b}\frac{1}{2}[f(\theta )-g(\theta )]^{2}d\theta$$

La idea de la deducción de esta formula es la misma idea al aproximar el área de una curva en coordenadas polares de esta sección, en este caso es sobre dos curvas.

En este tipo de coordenadas es un poco complicado dibujar este tipo de graficas por lo que hay algunas herramientas útiles en internet como Geogebra y Wolfram para visualizar estas curvas, incluso, si sabe programar, lo puede intentar con el lenguaje de programación de su agrado.

Tarea moral

Los siguientes ejercicios no son para evaluación pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionado con el tema visto.

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Deduzca la formula para calcular el área entre dos curvas en coordenadas polares.
  2. Encuentre el área de la región acotada por: $r=\sqrt{\theta}$.
  3. Encuentre el área de la región acotada por: $r=\theta^{2}$ y el sector$0\leq \theta \leq \frac{\pi}{4}$.
  4. Encuentre el área de la región acotada por: $r=e^{\frac{\theta}{2}}$ y el sector$0\leq \theta \leq 2\pi$.
  5. Encuentre el área de la región acotada por: $r=\sqrt{sin(\theta)}$ y el sector$0\leq \theta \leq \pi$.
  6. Encuentre el área de la región acotada por el circulo $r=1$ y fuera del cardioide $r=1-\cos(\theta)$.

Más adelante…

En esta sección vimos como calcular el área de una curva en coordenadas polares y entre dos curvas, obsérvese que la idea de calcular estas áreas es la misma que en coordenadas cartesianas, al igual, la idea de calcular la longitud de arco en coordenadas polares será la misma que en coordenadas cartesianas, el calculo de la longitud de arco con curvas polares lo veremos en la siguiente sección.

Entradas relacionadas

Cálculo Diferencial e Integral II: Coordenadas Polares

Por Miguel Ángel Rodríguez García

Deja un comentario

Introducción

En las secciones anteriores vimos una introducción a las curvas paramétricas, así como calcular las tangentes a estas curvas. En esta sección veremos una introducción a las coordenadas polares, ya que es importante en las matemáticas y futuras materias en su estudio.

Coordenadas polares

Las coordenadas polares son un sistema coordenado bidimensional en el que un punto en este plano es determinado por una distancia y un ángulo. El origen $O$ es llamado polo, y una semirrecta desde $O$ se llama eje polar como en la figura $(1)$, este eje generalmente se traza horizontalmente a la derecha correspondiente a la parte positiva del eje $x$ en las coordenadas cartesianas.

Figura 1: Coordenadas polares.

Sea $P$ un punto cualquiera en el sistema coordenado, entonces su distancia de $O$ a $P$ es $r$ denominándose distancia radial o radio vector y $\theta$ es el ángulo entre el eje polar y la recta $OP$ denominada como ángulo polar o coordenada angular, este ángulo generalmente se mide en radianes, por lo que el punto $P$ representa el par ordenado $P(r, \theta)$ y $r$, $\theta$ se llaman coordenadas polares del punto $P$.

$\theta$ es positivo cuando se mide en sentido contrario a las manecillas del reloj y negativo cuando se mide en sentido a las manecillas del reloj, mientras que $r$ siempre es mayor o igual a cero $(r \geq 0)$, en el caso del origen, el valor de $r$ es cero, pero el valor de $\theta$ se indefine, por lo que se define el valor en el origen como $(0, 0^{\circ})$.

Veamos unos ejemplos sencillos.

  • Graficar los siguientes puntos cuya coordenadas son: $A=(1, \frac{\pi}{4})$, $B=(2, 3\pi)$ y $C=(1, \frac{5\pi}{4})$

Para graficar los puntos en coordenadas polares es sencillo, nos fijamos en la coordenada angular de cada punto y partimos del eje polar, dibujando los ángulos de cada punto con su respectivo radio vector como se muestra en la figura $(2)$. Vemos en el caso del punto $B$ en donde la coordenada angular es $3\pi$ por lo que se tiene que dar una vuelta completa $(2\pi)$ más $pi$.

Figura 2: Visualización de los puntos A, B y C en coordenadas polares.

Conversión de coordenadas

Para pasar de las coordenadas cartesianas a las coordenadas polares, veamos la siguiente figura:

Figura 3: Relación entre coordenadas polares y cartesianas.

Vemos que el punto $O$ es el origen de las coordenadas cartesianas que coincide con el origen de las coordenadas polares, sea un punto cualquier $P$ con coordenadas cartesianas $P(x, y)$ y coordenadas polares $P(r, \theta)$ en el plano, formando un triángulo rectángulo y sabemos que:

$$\cos(\theta )=\frac{x}{r} \hspace{1.5cm}\sin(\theta )=\frac{y}{r}$$

Por tanto:

$$ x=r\cos(\theta )\hspace{1.5cm} y=r\sin(\theta) \tag{1}$$

A estas dos ecuaciones $(1)$ nos permite cambiar de coordenadas polares a coordenadas cartesianas. Para coordenadas cartesianas a coordenadas polares tenemos la siguiente relación:

$$r^{2}=x^{2}+r^{2} \hspace{1.5cm}\tan(\theta )=\frac{y}{x}$$

Se dejará como tarea moral deducir las relaciones anteriores.

Observación: Vea que en el caso de $r$ se tiene dos soluciones, pero sabemos que se toma el valor positivo. En el caso de calcular la coordenada angular, al despejar la variable $\theta$ tendremos la función tangente inversa, el cual el dominio es $(\frac{-\pi}{2}, \frac{\pi}{2} )$, para obtener un único valor de $\theta$ en el intervalo $[0, 2\pi)$ nos basamos en la siguiente fórmula:

$$\theta =  \left\{ \begin{array}{c}\arctan\left( \frac { y }{ x } \right) \quad ~ ~ ~~~~si~ x<0,~ y\leq 0 \\ \frac { \pi }{ 2 } ~ ~ ~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~ ~ ~ ~ ~ si~ x=0,~ y>0 \\ arctan\left(\frac{y}{x}\right) +\pi~ si~ x<0 \\ \frac { 3\pi }{ 2 } ~ ~ ~ ~ ~ ~ ~~~~~~~~~~~~~~~~ ~ ~ ~ ~ si~ x=0,~ y<0 \\ \arctan\left( \frac { y }{ x } \right) +2\pi ~ ~ si~ x=0,~ y<0 \end{array}\right.$$

Veamos un ejemplo:

  • Convierta el punto $(2, \frac{\pi}{3})$ de coordenadas polares a coordenadas cartesianas.

Por la relación (1) tenemos que:

$x=r\cos(\theta )=2\cos(\frac{\pi}{3})=2\frac{1}{2}=1$

$y=r\sin(\theta)=2\sin(\frac{\pi}{3})=2\frac{\sqrt{3}}{2}=\sqrt{3}$

Por tanto el punto en coordenadas cartesianas es: $(1, \sqrt{3})$

Tarea moral

Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Convierta los siguientes puntos en coordenadas cartesianas a coordenadas polares: $(-2, 2)$, $(-3, -3)$, $(4, -2)$.
  2. Deduzca la relación para pasar de coordenadas cartesianas a coordenadas polares.
  3. ¿Qué curva representa la ecuación polar $r=2$?
  4. Determinar la ecuación polar para la circunferencia $x^{2}+(y-3)^{2}=9$
  5. Bosqueje la curva $r=1+\sin(\theta)$

Más adelante…

En esta sección vimos una introducción a las coordenadas polares y como pasar de estas coordenadas a las coordenadas cartesianas y viceversa, en la siguiente sección veremos algunas figuras en estas coordenadas y calcularemos el área de una curva polar.

Entradas relacionadas