Introducción

El contenido de esta sección se basa predominantemente en el libro
Wheeden, R.L., Zygmund, A., Measure and Integral. An Introduccion to Real Analysis. (2da ed.). New York: Marcel Dekker, 2015, págs 17-22.

Estamos por presentar las últimas notas de blog del curso de Análisis Matemático I. Pretendemos mostrar un puente entre lo que vimos aquí y lo que se aprenderá en Análisis Matemático II. Conoceremos algunas ideas que, eventualmente, nos llevarán al concepto de la integral de Riemann-Stieltjes, un concepto que generaliza a la integral de Riemann (que suele verse en los cursos de Cálculo) pero que también es un caso particular de la integral de Lebesgue, la que se verá en la siguiente sección del blog. Para comenzar, analicemos los cambios que una función va tomando en un dominio cerrado.

Definición. Partición de un intervalo $\textbf{[a,b].}$ Sea $[a,b]$ un intervalo de $\mathbb{R}.$ Si $P = \{x_0=a, \, x_1, \, x_2,…,x_{n-1}, \, x_n = b\}, \, i=0,1,2,…,n \,$ es una colección de puntos tales que $x_0 =a, \, x_n = b$ y para cada $i =1,2,…,n$ se cumple que $x_{i-1}< x_i,$ entonces diremos que $P$ es una partición de $[a,b].$

Definición. Variación de $f$ sobre $[a,b].$ Considera una función $f:[a,b] \subset \mathbb{R} \to \mathbb{R} \,$ y sea $P=\{x_0, \, x_1, \, …, \, , x_n\}$ una partición de $[a,b].$ Definimos $S_P[f;a,b]$ (o bien $S_P$ cuando no hay necesidad de especificar la función y el intervalo) como:
$$S_P[f;a,b] := \sum_{i=1}^{n}|f(x_i) \, -\, f(x_{i-1})|$$

Entonces se suman las distancias que se generan al evaluar $f$ en cualesquiera dos puntos consecutivos de la partición.

Ya que para cada partición $P$ de $[a,b]$ existe su respectiva $S_P,$ podemos pensar en si la colección de todas las sumas tiene supremo. El supremo de las sumas de todas las particiones de $[a,b]$ recibe el nombre de variación de $f$ sobre $[a,b].$ Se denota como:
$$ \underset{P \, \in \, \mathcal{P_{[a,b]}}}{sup} \, S_P \, :=V[f;a,b] \, := V [a,b]\, := V$$

Donde $\mathcal{P}_{[a,b]} \,$ es el conjunto de particiones de $[a,b].$

Definición. Función de variación acotada y de variación no acotada. Sea $f:[a,b] \to \mathbb{R}.$ Considera $V[f;a,b].$ Si el supremo de hecho existe en $\mathbb{R},$ entonces $0 \leq V$ y diremos que $f$ es de variación acotada en $[a,b].$
En otro caso diremos que $V = \infty \,$ y que $f$ es de variación no acotada.

Ejemplos de variación en funciones

A continuación presentamos las variaciones de algunas funciones. Al final de esta sección te pediremos calcular los resultados formalmente.

Las siguientes son propiedades de las funciones de variación acotada.

Proposición. Si $f$ es de variación acotada en $[a,b]$ entonces $f$ es acotada en $[a,b].$

Demostración:
Sea $x \in [a,b].$ Considera la partición $\{a, \, x, \, b\},$ entonces
$$|f(x) \, – \, f(a)| \leq |f(x) \, – \, f(a)| +|f(b) \, – \, f(x)| \leq V.$$
Por lo tanto, $f$ es acotada en $[a,b].$

El regreso no es cierto, esto es, podemos tener una función acotada en $[a,b]$ pero que no sea de variación acotada. La función de Dirichlet ejemplifica esta situación. (Podrás ver otro caso también en la tarea moral de la siguiente entrada).

Proposición. Sean $f,g \,$ funciones de variación acotada en $[a,b]$ y sea $c \in \mathbb{R}.$ Entonces las funciones

• $cf,$
• $f+g \,$ y
• $fg$

son de variación acotada en $[a,b].$ Además

• $\dfrac{f}{g}$

también es de variación acotada en $[a,b]$ si existe $\varepsilon >0$ tal que $|g(x)| \geq \varepsilon$ para $x \in [a,b].$ La demostración queda como ejercicio.

Con las siguientes ideas tendremos recursos para aproximar mejor el valor de $V$ de una función.

Definición. Refinamiento. Sean $P,Q \in \mathcal{P}_{[a,b]} \,$ tales que $P \subseteq Q,$ es decir, $Q$ tiene todos los puntos de $P$ y, posiblemente, algunos otros. Entonces decimos que $Q$ es un refinamiento de $P,$ o que $Q$ refina a $P.$

Proposición. Si $Q$ es un refinamiento de $P,$ entonces $S_P \leq S_Q.$ La demostración la dejamos como ejercicio.

Proposición. Sea $f:[a,b] \to \mathbb{R}.$ Si $[a’,b’] \subseteq [a,b]$ entonces $V[a’,b’] \leq V[a,b],$ es decir, la variación potencialmente incrementa con el intervalo.

Demostración:
Sea $P= \{x_0= a’,…,x_n=b’\} \,$ una partición de $[a’,b’]$ y sea $Q = P \cup \{a,b\}.$ Claramente, $Q$ es partición de $[a,b]$ y
\begin{align*}
S_P[f;a’,b’] &= \sum_{i=1}^{n}|f(x_i) \, -\, f(x_{i-1})|\\
&\leq \sum_{i=1}^{n}|f(x_i) \, -\, f(x_{i-1})|+|f(x_0) \, -\, f(a)|+|f(b) \, -\, f(x_{n})|\\
&= S_Q[f;a,b]
\end{align*}

lo cual indica que para cada $S_P, \, P \in \mathcal{P}_{[a’,b’]}$ existe $S_Q, \, Q \in \mathcal{P}_{[a,b]}$ tal que $S_P \leq S_Q.$ Por lo tanto $V[a’,b’] \leq V[a,b].$

Proposición. Sea $f:[a,b] \to \mathbb{R}.$ Si $a < c < b$ entonces
$$V[a,b] = V[a,c] + V[c,b].$$
Es decir, la variación es aditiva en intervalos adyacentes.

Demostración:
Probemos primero que $V[a,c] + V[c,b] \leq V[a,b].$ Sea $P_1$ y $P_2$ particiones de $[a,c]$ y $[c,b],$ respectivamente. Entonces $P = P_1 \cup P_2$ es una partición de $[a,b].$

En consecuencia
$$S_{P_1}[f,a,c]+S_{P_2}[f,c,b] = S_P[f,a,b].$$
Ya que aún podrían existir otros valores más grandes de $S_{P’}[f,a,b]$ con $P’$ partición de $[a,b],$ se sigue que $V[a,c] + V[c,b] \leq V[a,b].$

Ahora probemos que $V[a,b] \leq V[a,c] + V[c,b].$ Sea $P$ una partición de $[a,b]$ y $\hat{P}= P \cup \{c\}.$

Entonces $\hat{P}$ es un refinamiento de $P,$ y por la proposición que dejamos al lector tenemos
$$S_P[f,a,b] \leq S_{\hat{P}}[f,a,b] = S_{P_1}[f,a,c]+S_{P_2}[f,c,b]$$
donde $P_1= \hat{P} \cap [a,c]$ y $P_2 = \hat{P} \cap [c,b].$
Por lo tanto $V[a,b] \leq V[a,c] + V[c,b],$ con lo que concluimos que

$$V[a,b] = V[a,c] + V[c,b].$$

Definición. Partes positiva y negativa de $x.$ Para cualquier $x \in \mathbb{R}$ definimos la parte positiva de $x$ como:

\begin{equation*}
x^+ = \begin{cases}
x & \text{si $x >0$} \\
0 & \text{si $x \leq 0$}
\end{cases}
\end{equation*}

Y la parte negativa de $x$ como:

\begin{equation*}
x^- = \begin{cases}
0 & \text{si $x >0$} \\
-x & \text{si $x \leq 0$}
\end{cases}
\end{equation*}

Nota que las partes positiva y negativa de un número real, satisfacen las siguientes relaciones:

1. $x^+,x^- \geq 0.$
2. $|x|=x^++x^- .$
3. $x = x^+-x^- .$

Definición. Suma de términos positivos y suma de términos negativos de $S_P.$ Sea $f:[a,b] \to \mathbb{R} \,$ y $P=\{x_0, \, x_1, \, … \, , x_{n-1}, \, x_n\}.$ Definimos la suma de términos positivos de $S_P$ como:

$$S_P^+:=S_P^+[f;a,b]:= \sum_{i =1}^{n} \, (f(x_i)-f(x_{i-1}))^+.$$

Y la suma de términos negativos de $S_P$ como:

$$S_P^-:=S_P^-[f;a,b]:= \sum_{i =1}^{n} \, (f(x_i)-f(x_{i-1}))^-.$$

En la siguiente imagen, las líneas naranjas representan los sumandos distintos de cero en $S_P^+$ y las líneas verdes, los de $S_P^-.$

Es sencillo comprobar que

\begin{align}
S_P^+ + S_P^- &= S_P \, \, \, \text{ y } \\
S_P^+ \, – \, S_P^- &=f(b) – f(a).
\end{align}

Definición. Variación positiva y variación negativa de $f.$ Definimos la variación positiva de $f$ como:

$$S^+:=S^+[f;a,b]:= \underset{P \in \mathcal{P}}{sup \, } \, S_P^+$$

Y la variación negativa de $f$ como:

$$S^-:=S^-[f;a,b]:= \underset{P \in \mathcal{P}}{sup \,} \, S_P^-$$

Nota que ambas son mayores iguales que cero y pueden valer $\infty$ cuando no existe el supremo en $\mathbb{R}.$

Proposición. Si alguno de $S^+, \, S^-, \, $ o $V$ es finito entonces los tres son finitos. Más aún, se satisface:

\begin{align}
S^++S^- &=V, \\
S^+-S^- &= f(b)-f(a)
\end{align}

o equivalentemente

\begin{align}
S^+&= \frac{1}{2}[V+f(b)-f(a)], \\
S^-&= \frac{1}{2}[V-f(b)+f(a)]
\end{align}

Demostración:
Supongamos que $V$ es finito. Por (1)
$$S_P^+ + S_P^- = S_P$$
y como $S_P \leq V,$ se sigue que
\begin{align*}
S_P^+ + S_P^- \leq V.
\end{align*}

Ya que tanto $S_P^+$ como $S_P^- $ son no negativos, tenemos
$$S_P^+ \leq V \, \Rightarrow \, S^+ \leq V.$$
De igual manera
$$S_P^- \leq V \, \Rightarrow \, S^- \leq V.$$

Por lo tanto, si $V$ es finito, $S^+$ y $S^-$ también lo son.

Ahora supongamos que $S^+$ es finito. Despejando en (2), se cumple:

\begin{align*}
&& S_P^- &= S_P^+ – \, (f(b) \, – \, f(a))\\
& \Rightarrow & &\leq S^+ – \, (f(b) \, – \, f(a))\\
\end{align*}

De modo que el conjunto de sumas de términos negativos está acotado y por lo tanto $S^-$ también es finito.

Por (1)
\begin{align}
\nonumber && S_P = S_P^+ + S_P^- &\leq S^+ + S^- \\
&\Rightarrow& V &\leq S^+ + S^-
\end{align}

En consecuencia, $V$ es finito.
Análogamente, podemos concluir que si $S^-$ es finito, $S^+$ y $V$ son finitos.

Para probar (4) considera una sucesión de particiones $(P_n)_{n \in \mathbb{N}} \,$ tal que la sucesión de sumas positivas cumple que

$$(S_{P_n}^+) \, \to \, S^+.$$

Vamos a demostrar que también $(S_{P_n}^-) \, \to \, S^-$ y que $S^+ \, – \, (f(b)\, – \, f(a)) = S^-,$ que es equivalente a (4).

Por (2) tenemos que $S_{P_n}^- = S_{P_n}^+- \, (f(b) \, – \, f(a)) ,$
y como $(S_{P_n}^+) \, \to \, S^+$
entonces $S_{P_n}^+- \, (f(b) \, – \, f(a)) \, \to \, S^ + -\, (f(b) \, – \, f(a)),$
y por transitividad
\begin{align}
S_{P_n}^- \, \to \, S^ + -\, (f(b) \, – \, f(a)).
\end{align}

Dado que $S_{P_n}^ – \leq S^ -,$ se sigue
\begin{align}
S^ + – \, (f(b) \, – \, f(a)) \leq S ^-.
\end{align}

Queremos que se cumpla la igualdad. Supón por el contrario que

$$S^ + – \, (f(b) \, – \, f(a)) < S ^-,$$

como $S ^-$ es el supremo de las sumas negativas, existe una partición $P$ de $[a,b]$ tal que

\begin{align}
&&S^ + – \, (f(b) \, – \, f(a))&<S_P ^- \\
&\Rightarrow& S^ + &<S_P ^- + (f(b) \, – \, f(a)) \\
&& &= S_P^+
\end{align}

lo cual es una contradicción, pues $S ^+$ es el supremo de las sumas positivas. Por lo tanto

\begin{align}
S^ + – \, (f(b) \, – \, f(a)) = S ^-,
\end{align}

Lo que prueba (4),

y por (8)
\begin{align}
S_{P_n} ^- \, \to \, S ^-,
\end{align}

Por otro lado, por (1)
$$S_{P_n}^+ + S_{P_n}^- = S_{P_n} \leq V$$
de modo que tomando el límite
\begin{align}
S^+ + S^- \leq V
\end{align}

y de (7) y (15) concluimos finalmente

$$S^+ + S^- = V$$

que es (3).

Finalizamos esta sección con el siguiente

Corolario. Teorema de Jordan. Una función $f:[a,b] \to \mathbb{R}$ es de variación acotada en $[a,b]$ si y solo si puede ser expresada como la diferencia de dos funciones crecientes acotadas en $[a,b].$

Demostración:
Supón que $f$ es de variación acotada. Por un resultado visto arriba, sabemos que $f$ es de variación acotada en cada subintervalo $[a,x]$ con $x \in [a,b].$ Para cada $x,$ sean $S(x) ^+$ y $S(x) ^-$ las variaciones positiva y negativa de $f$ en $[a,x].$ Es sencillo demostrar que estas funciones son crecientes y acotadas en $[a,b],$ (ver tarea moral), y aplicando el teorema anterior en cada $[a,x],$
\begin{align*}
&& S(x) ^+ \, – \, S(x) ^- &= f(x) \, – \, f(a) \\
&\Rightarrow&f(x) &= (S(x) ^+ +f(a)) \, – \, S(x) ^-
\end{align*}

Como $S(x)$ es creciente y acotada, también lo es $(S(x) ^+ +f(a))$, de modo que $f$ es la diferencia de dos funciones crecientes y acotadas.

En contraparte, supongamos que $f = f_1 \, – \, f_2,$ donde $f_1$ y $f_2$ son funciones crecientes y acotadas en $[a,b].$ De acuerdo con el primer ejemplo, ambas funciones son de variación acotada. Finalmente, por un resultado enunciado arriba, $ f_1 \, – \, f_2 = f \,$ es de variación acotada.

Más adelante…

Seguiremos con el estudio de las funciones de variación acotada y conectaremos con curvas rectificables, una concepción de cómo considerar la longitud de una curva que podría no coincidir, con medir la gráfica de la misma.

Tarea moral

1. Verifica la variación de cada función de los ejemplos enunciados arriba.
2. Demuestra que si $f,g \,$ son funciones de variación acotada en $[a,b]$ y $c \in \mathbb{R},$ entonces las funciones
   $$cf, \, f+g \, \, \text{ y } \, \, fg$$
   son de variación acotada en $[a,b].$ Además
   $$\frac{f}{g}$$
   también es de variación acotada en $[a,b]$ si existe $\varepsilon >0$ tal que $|g(x)| \geq \varepsilon$ para $x \in [a,b].$
3. Prueba que si $Q$ es un refinamiento de $P,$ entonces $S_P \leq S_Q.$
4. Para cada $x,$ sean $S(x) ^+$ y $S(x) ^-$ las variaciones positiva y negativa de $f$ en $[a,x].$ Demuestra que estas funciones son crecientes y acotadas en $[a,b].$
5. Prueba que si $f:[a,b] \to \mathbb{R}$ es Lipschitz continua, entonces es de variación acotada.

Bibliografía

• Wheeden, R.L., Zygmund, A., Measure and Integral. An Introduccion to Real Analysis. (2da ed.). New York: Marcel Dekker, 2015. Págs: 17-22.

Enlaces

• Análisis Matemático.
• Guía de notación para Análisis Matemático I
• Enlace a entrada anterior.
• Enlace a entrada siguiente.

Introducción

En la entrada anterior trabajamos con la ecuación diferencial $\dfrac{d \, y(x)}{dx} = y(x)$ con condición inicial $y(0)=1.$ Al identificar propiedades enunciadas en el teorema de punto fijo de Banach encontramos su solución. En esta ocasión repetiremos el proceso para demostrar que la solución a una ecuación diferencial general existe y es única.

Primeramente, veamos un concepto.

Definición. Función localmente Lipschitz continua en la segunda variable. Sea $(a,b) \subset \mathbb{R}$ y sea $\Omega \subset \mathbb{R}$ tal que $\Omega$ es abierto. Si $F:(a,b) \times \Omega \to \mathbb{R}$ es una función que satisface que para cada $x_0 \in (a,b)$ y $y_0 \in \Omega \, $ existen $\delta_0 >0$ y $c \in \mathbb{R}$ tales que $[x_0 – \delta_0, x_0 + \delta_0] \subset (a,b), \, [y_0 – \delta_0, y_0 + \delta_0] \subset \Omega$ y además que si $x \in [x_0 – \delta_0, x_0 + \delta_0] $ y si $y_1,y_2 \in [y_0 – \delta_0, y_0 + \delta_0]$ entonces
$$|F(x,y_1)-F(x,y_2)| \leq c |y_1-y_2|$$
diremos que $F$ es localmente Lipschitz continua en la segunda variable.

Solución a la ecuación diferencial $\dfrac{d \, y(x)}{dx}=F(x,y(x))$

Sea $\dfrac{d \, y(x)}{dx}=F(x,y(x))$ una ecuación diferencial con condición inicial $y(x_0)=y_0$ donde:

1. $F$ es una función continua y localmente Lipschitz continua en la segunda variable.
2. $y \,$ es una función, al menos derivable, de variable $x$ que manda valores reales en valores reales.
3. $x_0$ es un punto donde la $\, y \,$ buscada toma valor $y_0.$

Plan para resolverla con el teorema de punto fijo de Banach: Propondremos un espacio métrico completo $(X,d)$ de funciones entre las cuales deberá estar la $\, y \,$ buscada y una contracción $\phi:X \to X$ cuyo punto fijo sea la solución de la ecuación diferencial.

Sean $\delta_0>0$ y $c>0$ para $F$ localmente Lipschitz continua como en la definición. Dada la continuidad de $F,$ la función restringida en el conjunto $[x_0 \, – \, \delta_0, x_0 + \delta_0] \times [y_0 \, – \, \delta_0, y_0 + \delta_0]$ es continua y acotada por lo tanto podemos elegir existe $M \geq 1$ tal que para toda $(x,y) \in [x_0 \, – \, \delta_0, x_0 + \delta_0] \times [y_0 \, – \, \delta_0, y_0 + \delta_0]$ se cumple
$$|f(x,y)| \leq M.$$

Sea $\delta$ tal que $0< \delta < min\{\frac{1}{c}, \frac{\delta_0}{M}\}$

Considera $X:= \{f \in \mathcal{C}^0([x_0 \, – \, \delta, x_0 + \delta],\mathbb{R}) \, | \, d_{\infty}(f,y_0) \leq \delta M \}$
donde $y_0$ representa, en este caso, a la función constante que arroja el valor $y_0.$ Nota que $X$ es un espacio cerrado en el espacio métrico $\mathcal{C}^0([x_0 \, – \, \delta, x_0 + \delta],\mathbb{R})$ que recordemos, tiene la propiedad de ser completo (lo probamos en Convergencia uniforme y continuidad). Por lo visto en la última proposición de la entrada Espacios métricos completos concluimos que $X$ también es completo.

Propongamos la contracción $\phi$ deseada

Si $f \in X$ satisface la ecuación diferencial entonces para todo $x \in [x_0 \, – \, \delta, x_0 + \delta]$ se sigue:

\begin{align*}
&&\dfrac{d \, f(x)}{dx}&= F(x,f(x))\\
&\Rightarrow & \int_{x_0}^{x} \dfrac{d \, f(t)}{dt} \, dt &= \int_{x_0}^{x} F(t,f(t)) \, dt\\
&\Rightarrow & f(x) \, – \, f(x_0) &=\int_{x_0}^{x} F(t,f(t)) \, dt\\
&\Rightarrow & f(x) &=f(x_0) + \int_{x_0}^{x} F(t,f(t)) \, dt\\
&\Rightarrow & f(x) &= y_0 + \int_{x_0}^{x} F(t,f(t)) \, dt
\end{align*}

Como buscamos que esta solución sea punto fijo de una contracción $\phi$ en $X$ entonces $\phi(f(x)) = f(x).$ La última igualdad nos lleva a proponer:

$$\phi(f(x)) := y_0 + \int_{x_0}^{x} F(t,f(t)) \, dt$$

Nota que $\phi(f(x))$ pertenece a $\mathcal{C}^0([x_0 – \delta, x_0 + \delta],\mathbb{R}).$ Probaremos que también pertenece a $X.$ Si $x \in [x_0 – \delta, x_0 + \delta],$ tenemos dos casos:

De ambos casos podemos concluir que $d_{\infty}(f,y_0) \leq \delta M,$ por lo tanto $\phi(f) \in X.$

$\phi$ es contracción en $X$

Sean $f,g \in X.$ Considera $I = [x_0 – \delta, x_0 + \delta]$ entonces si $x \in I,$ tenemos dos casos.

Si $x < x_0.$

\begin{align*}
|\phi(f(x))- \phi(g(x))|&=\left|y_0 + \int_{x_0}^{x} F(t,f(t)) \, dt-(y_0 + \int_{x_0}^{x} F(t,g(t)) \, dt) \right|\\
&=\left|\int_{x_0}^{x} F(t,f(t)) \, dt- F(t,g(t)) \, dt \right|\\
&=\left|- \int_{x}^{x_0} F(t,f(t)) \, dt- F(t,g(t)) \, dt \right|\\
&=\left| \int_{x}^{x_0} F(t,f(t)) \, dt- F(t,g(t)) \, dt \right|\\
&\leq \int_{x}^{x_0} |F(t,f(t)) \, dt- F(t,g(t))| \, dt\\
&\leq \int_{x}^{x_0} c|f(t)- g(t)| \, dt \\
&\leq (x_0-x) c \, d_{\infty}(f,g) \\
&\leq (\delta c) \, d_{\infty}(f,g)
\end{align*}

Por lo tanto, la distancia entre $\phi(f)$ y $\phi(g)$ se puede estimar como

\begin{align*}
d_\infty(\phi(f(x)), \phi(g(x))) &= \underset{x \in I}{sup} \, |\phi(f(x))- \phi(g(x))| \\
&\leq \underset{x \in I}{sup} \, \delta c \, d_{\infty}(f,g) \\
&=(\delta c)d_{\infty}(f,g)
\end{align*}

Sea $\alpha := \delta c$ entonces $\alpha<1,$ por lo tanto $\phi$ es contracción en $X.$

Lo que hemos visto en esta entrada demuestra el siguiente:

Teorema. Picard-Lindelöf. Sea $F:(a,b) \times \Omega \to \mathbb{R}$ una función continua y localmente Lipschitz continua en la segunda variable. Entonces, dados $x_0 \in (a,b)$ y $y_0 \in \Omega$ existe $\delta >0$ tal que la ecuación diferencial
$$\dfrac{d \, y(x)}{dx}=F(x,y(x)), \, y(x_0)=y_0$$
tiene una única solución en el intervalo $[x_0 \, – \, \delta, x_0 + \delta].$

Generalización en $\mathbb{R}^n$

Si $\Omega \subset \mathbb{R}^n$ y $F$ tiene su contradominio en $\mathbb{R}^n$ entonces la definición y el teorema quedan como sigue:

Definición. Función localmente Lipschitz continua en la segunda variable. Sea $(a,b) \subset \mathbb{R}$ y sea $\Omega \subset \mathbb{R}^n$ tal que $\Omega$ es abierto. Si $F:(a,b) \times \Omega \to \mathbb{R}^n$ es una función que satisface que para cada $x_0 \in (a,b)$ y $y_0 \in \Omega \, $ existen $\delta_0 >0$ y $c>0$ tales que $[x_0 – \delta_0, x_0 + \delta_0] \subset (a,b), \, \overline{B}(y_0, \delta_0) \subset \Omega$ y además que si $|x-x_0| \leq \delta_0$ y si $y_1,y_2 \in \overline{B}(y_0,\delta_0)$ entonces
$$\norm{F(x,y_1)-F(x,y_2)} \leq c \norm{y_1-y_2}$$
diremos que $F$ es localmente Lipschitz continua en la segunda variable.

Teorema. Picard-Lindelöf. Sea $F:(a,b) \times \Omega \to \mathbb{R}^n$ una función continua y localmente Lipschitz continua en la segunda variable. Entonces, dados $x_0 \in (a,b)$ y $y_0 \in \Omega$ existe $\delta >0$ tal que la ecuación diferencial
$$\dfrac{d \, y(x)}{dx}=F(x,y(x)), \, y(x_0)=y_0$$
tiene una única solución en el intervalo $[x_0 \, – \, \delta, x_0 + \delta].$

En este caso el espacio completo donde podemos encontrar la solución es

$$X:= \{ f \in \mathcal{C}^0([x_0 \, – \, \delta, x_0 + \delta], \mathbb{R}^n) : \norm{f \, – \, y_0}_\infty \leq \delta M\}$$

Donde $\delta$ y $M$ se definen de forma análoga a la demostración anterior.

Más adelante…

Pasaremos a la siguiente sección de esta asignatura con temas de compacidad. Aunque ya se han usado algunos resultados para el caso del espacio métrico euclidiano, mostraremos cómo el concepto puede generalizarse en otros espacios a partir de la topología que la métrica induce en ellos.

Tarea moral

1. Sea $F: \mathbb{R} \times \mathbb{R} \to \mathbb{R}$ tal que
   \begin{equation*}
   F (x,y):= \begin{cases}
   0 & \text{si $x=0$} \\
   \frac{y}{x} & \text{si $x \neq 0$}
   \end{cases}
   \end{equation*}
   Prueba que $F(x,y)$ es localmente Lipschitz continua en la segunda variable, pero no es continua en $(0,0).$
2. Sea $F: \mathbb{R} \times \mathbb{R} \to \mathbb{R}$ tal que $F(x,y):= 3y^{2/3}.$
   a) Prueba que $F$ no es localmente Lipschitz continua en la segunda variable.
   b) Prueba que para cualesquiera $\alpha < 0 < \beta,$ la función
   \begin{equation*}
   f_{\alpha, \beta}(x) := \begin{cases}
   (x \, – \, \alpha)^3 & \text{si x $\leq \alpha,$} \\
   0 & \text{si $\alpha \leq x \leq \beta,$}\\
   (x \, – \, \beta)^3 & \text{si $x \geq \beta.$}
   \end{cases}
   \end{equation*}
   Es diferenciable en $\mathbb{R}$ y es solución de
   $$\dfrac{d \, y(x)}{dx}=3y^{2/3}, \, y(0)=0.$$
   Así, si $F$ no es localmente Lipschitz continua en la segunda variable la ecuación puede tener una infinidad de soluciones.
3. Sea $F: \mathbb{R} \times \mathbb{R} \to \mathbb{R}$ tal que $F(x,y)= -y^2.$
   a) Prueba que $F$ es localmente Lipschitz continua en la segunda variable.
   b) Para $\alpha \neq 0$ considera la ecuación
   $$\dfrac{d \, y(x)}{dx}=-y^2, \, y(0)= – \, \frac{1}{\alpha}.$$
   Prueba que $f(x)= \dfrac{1}{x \, – \, \alpha}$ es su solución en algún intervalo que contiene a $0.$
   c) ¿Cuál es el intervalo máximo para el que esta ecuación tiene solución?

Bibliografía

• Clapp, M., Análisis Matemático. Ciudad de México: Editorial Papirhos, IM-UNAM, 2013. Págs: 111-115, 119 y 120.
• Kolmogorov, A.N., Fomin, S.V., Elementos de la Teoría de Funciones y del Análisis Funcional. (2a ed.). Moscú: Editorial MIR, 1975. Págs: 83-86.

Enlaces

• Análisis Matemático.
• Guía de notación para Análisis Matemático I
• Enlace a entrada anterior.
• Enlace a entrada siguiente.

Introducción

En la sección La métrica de Hausdorff definimos que un conjunto acotado es aquel que está contenido en una bola del espacio métrico. Hay una propiedad más específica de los, así llamados, conjuntos totalmente acotados. Consiste en encerrar al conjunto en una unión de bolas abiertas tan pequeñas como se desee. La particularidad radica en que, por muy pequeño que sea el radio de estas bolas, bastará con una cantidad finita de ellas para cubrir todo el conjunto. Formalmente esta idea se expresa como:

Definición. Conjunto totalmente acotado. Sea $(X,d)$ un espacio métrico y $A \subset X.$ Si para todo $\varepsilon >0$ existe una cantidad finita de puntos $a_1,…,a_n \in A$ tales que
$$A \subset \underset{i =1,…,n}{\bigcup}\, B(a_i,\varepsilon)$$
diremos que $A$ es totalmente acotado.

Por supuesto que esta propiedad asegura que el conjunto sea acotado.

Proposición. Si $A \subset X$ es totalmente acotado, entonces $A$ es acotado.

Demostración:
Como $A$ es totalmente acotado, existen $a_1,a_2,…,a_n \in A$ tales que $A \subset \underset{i =1,…,n}{\bigcup}B(a_i,1).$ Ahora busquemos una bola abierta en $X$ que contenga al conjunto $A.$

Considera la máxima distancia entre $a_1$ y el resto de los centros. Llamémosla $M$ es decir, $M = max\{d(a_1,a_k) \, | \, k=2,…,n\}.$ A continuación identificaremos una bola abierta con centro en $a_1$ que cumplirá lo deseado.

Si $x \in A$ se tiene que $x \in B(a_k,1)$ para algún $k \in \{1,…,n\},$ así:
\begin{align*}
d(a_1,x)&\leq d(a_1,a_k) + d(a_k,x) \\
&< M + 1
\end{align*}

Por lo tanto $A \subset B(a_1,M+1),$ concluyendo así que $A$ es acotado.

Contrario a esto, (y como pudimos ver en la entrada anterior) en general no es cierto que todo conjunto acotado sea totalmente acotado:

Contraejemplo: Considera el espacio de las sucesiones en $\mathbb{R}$ dado por $\ell_1 =\{(x_n)_{n \in \mathbb{N}} \, | \, \sum_{n=1}^{\infty} |x_n| < \infty \}$ con la norma definida como $\norm{(x_n)}_1 := \sum_{n=1}^{\infty}|x_n|.$

Sea $A=\{e_i \, | \, i \in \mathbb{N}\}$ donde $e_i$ es la sucesión que toma a $1$ como valor en la entrada $i$ y $0$ en el resto.

Este conjunto es acotado en $\ell_1$ pues para cada $i \in \mathbb{N}, \, \norm{e_i}_1= \sum_{n=1}^{\infty}|x_n|= |1|=1$ de modo que $A \subset B(\mathcal{0},2)$ donde $\mathcal{0}$ es la sucesión constante cero.

No obstante, $A$ no es totalmente acotado. Si calculamos la distancia entre dos sucesiones en $A$ tenemos que para cualesquiera $i \neq j, \, d(e_i,e_j)= |1|+|1|= 2.$ Por lo tanto si se elige $\varepsilon >0,$ tal que $\varepsilon \leq 2$ cada bola de radio $\varepsilon$ con centro en alguna sucesión de $A$ excluye al resto de los elementos de $A$, de modo que no será posible cubrir $A$ con una cantidad finita de bolas de radio $\varepsilon$ cuyo centro esté en $A.$

Esto nos permite concluir que $A$ no es totalmente acotado.

El ejemplo nos incentiva algunas preguntas: ¿Es el conjunto $A$ cerrado en $\ell_1?$ ¿Es compacto? ¿Bastará con que un conjunto sea totalmente acotado para que sea compacto? Al final de esta sección podrás responderlas.

Por lo pronto veamos que la propiedad de ser totalmente acotado, se hereda en subconjuntos:

Proposición. Sea $A \subset X$ un conjunto totalmente acotado. Si $B \subset A$ entonces $B$ es totalmente acotado.

Proposición. Si $A \subset X$ es totalmente acotado entonces $\overline{A}$ también es totalmente acotado. La demostración se deja como ejercicio.

Proposición. Si $A \subset X$ es compacto entonces $A$ es totalmente acotado.

Demostración:
Sea $\varepsilon >0$ y $A$ un conjunto compacto. Para cada punto $a \in A$ considera $B(a,\varepsilon).$ Entonces el conjunto $\{B(a,\varepsilon) \, | \, a \in A\}$ es una cubierta abierta de $A.$

Como $A$ es compacto entonces existe una subcubierta finita $\{B(a_1,\varepsilon),B(a_2,\varepsilon),…,B(a_n,\varepsilon)\}.$ Por lo tanto, $A$ es totalmente acotado.

En general no es cierto que un conjunto totalmente acotado sea compacto. El regreso requiere de una propiedad más:

Proposición. $A \subset X$ es compacto si y solo si es completo y totalmente acotado.

Demostración:
Supón que $A$ es un conjunto compacto. Ya vimos que esto lo hace totalmente acotado, ahora comprobemos que también es completo. Sea $(x_n)_{n \in \mathbb{N}} \,$ una sucesión de Cauchy en $A.$ Por lo visto en la entrada de Compacidad en espacios métricos sabemos que $(x_n)$ tiene una subsucesión que converge en $A.$ Luego, por la entrada Sucesiones de Cauchy sabemos que esto permite concluir que $(x_n)$ es convergente, por lo tanto $A$ es completo.

En el regreso partimos de que $A$ es completo y totalmente acotado. Supongamos por el contrario que $A$ no es compacto. Entonces existe una cubierta abierta $\mathcal{C} = \{ A_i \, | \, i \in \mathcal{I} \}$ de $A$ tal que no tiene subcubierta finita.

Queda como ejercicio al lector demostrar que la sucesión $(x_n)$ es de Cauchy. Como $A$ es completo, se sigue que $x_n \to x^*$ para algún $x^* \in A.$

Sea $\mathcal{U} \in \mathcal{C}$ tal que $x^* \in \mathcal{U}.$ Como $\mathcal{U}$ es abierto, existe $\varepsilon >0$ tal que $B(x^*,\varepsilon) \subset \mathcal{U}.$ Como $x_n \to x^*$ existe $N \in \mathbb{N}$ tal que para cada $ \, k \geq N, d(x_k, x^*)< \frac{\varepsilon}{2}.$

Sea $K \in \mathbb{N}$ tal que $K > N$ y además, $\frac{1}{K} < \frac{\varepsilon}{2}.$ Demostraremos que $B(x_{K-1}, \frac{1}{K}) \subset \mathcal{U}.$

En consecuencia $B(x_{K-1}, \frac{1}{K}) \subset \mathcal{U}$ lo cual es una contradicción, pues habíamos dicho que no puede ser cubierto por una cantidad finita de elementos de $\mathcal{C}.$ Por lo tanto $A$ es un conjunto compacto.

Hemos visto que si un conjunto no es cerrado tampoco es compacto. No obstante puede ocurrir que la cerradura del conjunto sí lo sea. Tenemos la siguiente:

Definición. Conjunto relativamente compacto. Sea $(X,d)$ espacio métrico y sea $A \subset X.$ Diremos que $A$ es relativamente compacto si $\overline{A}$ es compacto.

Proposición. Sea $(X,d)$ un espacio métrico completo. Entonces $A \subset X$ es relativamente compacto en $X$ si y solo si es totalmente acotado.

Demostración:
Si $A$ es relativamente compacto entonces $\overline{A}$ es compacta en $X$ y por tanto, totalmente acotado. Como $A \subset \overline{A}$ concluimos por una proposición vista arriba que $A$ también es totalmente acotado.

Por otro lado, partiendo de que $A$ es totalmente acotado tenemos por la proposición que dejamos como ejercicio, que $\overline{A}$ también es totalmente acotado. Además, $\overline{A}$ es completo, pues es un subconjunto cerrado en $X$ completo, (ver Espacios métricos completos) así podemos concluir por la proposición de arriba, que $\overline{A}$ es compacto.

Más adelante…

Como hemos visto, la total acotación es la propiedad que nos permite decir que todos los puntos de un conjunto están muy cerca de una selección finita de puntos del conjunto. En la siguiente sección veremos cómo asegurar esto para espacios de funciones continuas a través de una propiedad conocida como equicontinuidad.

Tarea moral

1. Considera el espacio de las sucesiones en $\mathbb{R}$ dado por $\ell_1 =\{(x_n)_{n \in \mathbb{N}} \, | \, \sum_{n=1}^{\infty} |x_n| < \infty \}$ donde la norma se define como $\norm{(x_n)}_1 := \sum_{n=1}^{\infty}|x_n|.$ Sea $A=\{e_i \, | \, i \in \mathbb{N}\}$ donde $e_i$ es la sucesión que toma a $1$ como valor en la entrada $i$ y $0$ en el resto. ¿Es el conjunto $A$ cerrado en $\ell_1?$ ¿Es compacto?
2. Da un ejemplo de un conjunto totalmente acotado que no sea compacto.
3. Demuestra que si $A$ es totalmente acotado entonces $\overline{A}$ también es totalmente acotado.
4. Demuestra que la sucesión $(x_n)_{n \in \mathbb{N}} \,$ de la demostración de $»A \subset X$ es compacto si y solo si es completo y totalmente acotado«, es de Cauchy.
5. Sea $X$ un espacio métrico. Demuestra que si toda sucesión en $X$ tiene una subsucesión que converge en $X$ entonces es completo y totalmente acotado. Nota que es lo que falta para concluir que son equivalentes:
   a) $X$ es compacto.
   b) Toda sucesión en $X$ tiene una subsucesión que converge en $X.$
   c) $X$ es completo y totalmente acotado.

Bibliografía

• Apostol, T., Análisis Matemático (2a ed.). México: Editorial Reverté, 1996. Pág: 90.
• Clapp, M., Análisis Matemático. Ciudad de México: Editorial Papirhos, IM-UNAM, 2013. Págs: 121-125.
• Kolmogorov, A.N., Fomin, S.V., Elementos de la Teoría de Funciones y del Análisis Funcional. (2a ed.). Moscú: Editorial MIR, 1975. Págs: 110-115.

Enlaces

• Análisis Matemático.
• Guía de notación para Análisis Matemático I
• Enlace a entrada anterior.
• Enlace a entrada siguiente.

Introducción

Probablemente recuerdes de otros cursos términos que son de la forma $\sum_{k=1}^{\infty}\, a_k.$ Hacen alusión a una suma de infinitos términos. Deseamos que sea posible obtener un resultado de esta operación, pero no siempre existe. Para el caso en que los términos $a_k$ son números reales, puedes consultar las entradas Cálculo Diferencial e Integral II: Definición de series y series infinitas
Cálculo Diferencial e Integral II: Criterio de la divergencia y de acotación
Cálculo Diferencial e Integral II: Criterio de comparación y comparación del limite.

En esta sección trabajaremos con series en un espacio vectorial normado. Ya que estas se construyen a partir de sucesiones, podemos esperar que varios resultados de convergencia, vistos hasta el momento, encontrarán su versión en las sumas infinitas.

Definición. Suma parcial. Sea $V=(V, \norm{\cdot})$ un espacio vectorial normado y sea $(v_n)_{n \in \mathbb{N}} \,$ una sucesión en $V.$ Consideremos la suma de los primeros $n$ términos con $n \in \mathbb{N}.$ Se llama suma parcial y está dada por:

$$w_n:= \sum_{k=1}^{n} \, v_k.$$

Podemos pensar que conforme incrementa el valor de $n$ más términos de la sucesión son considerados en la suma. Se forma entonces una sucesión con los resultados $w_n. $ Así, $\, (w_n)_{n \in \mathbb{N}} \,$ es la sucesión de sumas parciales. ¿Será convergente?

Definición. Serie convergente. Sea $(v_n)_{n \in \mathbb{N}} \,$ una sucesión en $V=(V, \norm{\cdot}).$ Si la sucesión de sumas parciales $(w_n)_{n \in \mathbb{N}} \,$ converge en $V,$ decimos que la serie denotada como

$$\sum_{k=1}^{\infty} \, v_k$$

converge en $V$ y equivale al límite de las sumas parciales, es decir.

$$ \underset{n \to \infty}{lim} \, w_n \, := \, \sum_{k =1}^{\infty} \, v_k.$$

Dejaremos como ejercicio demostrar que si una serie converge, entonces su límite es único.

Se satisface la siguiente:

Proposición. Si la serie $\sum_{k=1}^{\infty} \, v_k$ converge en $V,$ entonces $(v_n)_{n \in \mathbb{N}} \,$ converge a $0$ en $V.$ Se sigue también que esta sucesión es acotada.

Demostración:
Sea $\varepsilon >0.$ Ya que $\sum_{k=1}^{\infty} \, v_k$ converge en $V,$ por definición, $(w_n)_{n \in \mathbb{N}} \,$ converge en $V$ y por tanto es de Cauchy, así existe $N \in \mathbb{N}$ tal que para cualesquiera $n,m \geq N,$

$$\norm{w_n-w_m} < \varepsilon$$

en particular, para cada $n \geq N$ se cumple

\begin{align*}
&&\norm{w_{n+1}-w_n} &< \varepsilon\\
&\iff& \norm{\sum_{k=1}^{n+1} v_k \, – \sum_{k=1}^{n} v_k} &< \varepsilon\\
&\iff& \norm{v_{n+1}} &< \varepsilon
\end{align*}

Por lo tanto $v_n \to 0$ en $V,$ y por lo visto en Convergencia (toda sucesión convergente es acotada), concluimos que $(v_n)_{n \in \mathbb{N}} \,$ es acotada.

Cuando el espacio normado $V$ es completo se tiene un resultado que muestra condiciones necesarias y suficientes para que una serie sea convergente:

Proposición. Criterio de Cauchy para series. Sea $V$ un espacio de Banach y sea $(v_n)_{n \in \mathbb{N}} \,$ una sucesión en $V.$ La serie $\sum_{k=1}^{\infty} \, v_k$ converge en $V$ si y solo si para cada $\varepsilon >0$ existe $N_0 \in \mathbb{N}$ tal que
$$\norm{v_{N+1}+…+v_{N+j}}< \varepsilon$$
para cualquier $N \geq N_0$ y cualquier $j \geq 1.$

Demostración:
Sea $\varepsilon > 0.$ La serie $\sum_{k=1}^{\infty} \, v_k$ converge en $V$ si y solo si $(w_n)_{n \in \mathbb{N}} \,$ converge en $V.$ Como $V$ es de Banach esto ocurre si y solo si $(w_n)_{n \in \mathbb{N}} \,$ es de Cauchy, es decir, si y solo si existe $N_0 \in \mathbb{N}$ tal que para cualesquiera $n,m \geq N_0,$
$$\norm{w_n -w_m} < \varepsilon$$
si y solo si para cualquier $N \geq N_0$ y cualquier $j \geq 1$, como $N+j > N \geq N_0$ se sigue que
\begin{align*}
&&\norm{w_{N+j} -w_{N}} < \varepsilon\\
&\Rightarrow &\norm{\sum_{k=1}^{N+j} v_k \, – \sum_{k=1}^{N} v_k} < \varepsilon\\
&\Rightarrow &\norm{v_{N+1}+…+v_{N+j}} < \varepsilon
\end{align*}

que es lo que queríamos demostrar.

Hay otra forma de asegurar la convergencia de una serie a partir de la convergencia de la serie formada por la norma de sus términos. Es decir:

Teorema. Criterio de Weierstrass. Sea $V$ un espacio de Banach y sea $(v_n)_{n \in \mathbb{N}} \,$ una sucesión en $V.$ Si la serie de números reales $\sum_{k=1}^{\infty} \, \norm{v_k}$ converge decimos que es absolutamente convergente. En este caso se cumple que la serie $\sum_{k=1}^{\infty} \, v_k$ converge en $V$ y además:
$$\norm{\sum_{k=1}^{\infty} \, v_k} \leq \sum_{k=1}^{\infty} \, \norm{v_k}.$$

Demostración:
Dado que $\sum_{k=1}^{\infty} \, \norm{v_k}$ converge en $\mathbb{R}$ que es de Banach, se sigue por la proposición anterior, que existe $N_0 \in \mathbb{N}$ tal que para cualquier $N \geq N_0$ y cualquier $j \geq 1$ se cumple
\begin{align*}
&&&|\, \norm{v_{N+1}}+…+\norm{v_{N+j}} \,|&< \varepsilon\\
&\Rightarrow &&\norm{v_{N+1}}+…+\norm{v_{N+j}}&< \varepsilon\\
&\Rightarrow &\norm{v_{N+1}+…+v_{N+j}}\leq &\norm{v_{N+1}}+…+\norm{v_{N+j}} &< \varepsilon.
\end{align*}

Nuevamente por la proposición anterior concluimos que la serie $\sum_{k=1}^{\infty} \, v_k$ converge en $V.$

Dado que para cada $n \in \mathbb{N}$ se cumple

\begin{align*}
&&\norm{\sum_{k=1}^{n}v_k} &\leq \sum_{k=1}^{n} \norm{v_k}\\
&\Rightarrow& \underset{n \to \infty}{lim} \, \norm{\sum_{k=1}^{n}v_k} &\leq \underset{n \to \infty}{lim} \, \sum_{k=1}^{n} \norm{v_k}\\
&\Rightarrow& \norm{\sum_{k=1}^{\infty} \, v_k} &\leq \sum_{k=1}^{\infty} \, \norm{v_k}.
\end{align*}

Con lo cual concluimos la demostración. Este teorema tiene su regreso en la siguiente:

Proposición. Sea $(V, \norm{\cdot})$ un espacio vectorial normado. Entonces $V$ es completo si y solo si toda serie en $V$ absolutamente convergente es convergente. La demostración del regreso se dejará como ejercicio.

Más adelante…

Ya que nos familiarizamos con la idea de las sumas infinitas, procederemos con unas que tendrán como términos funciones. Debido a que la suma de funciones es una función, de esta naturaleza será el límite.

Tarea moral

1. Demuestra que si una serie de un espacio vectorial normado es convergente, entonces su límite es único.
2. Sea $(V, \norm{\cdot})$ un espacio vectorial normado. Prueba que si toda serie en $V$ absolutamente convergente es convergente entonces $V$ es completo. A continuación una guía para la demostración:
   a) Sea $(v_n)_{n \in \mathbb{N}} \,$ una sucesión de Cauchy en $V.$ Construye una subsucesión $(v_{n_{k}})$ de $(v_n)$ tal que $\norm{x_{n_{k+1}}-x_{n_{k}}}< \frac{1}{2^k}.$
   b) Prueba que $\sum_{k=1}^{\infty}(x_{n_{k+1}}-x_{n_{k}})$ es convergente.
   c) Prueba que $(v_{n_{k}})$ converge y concluye que $(v_n)$ es convergente.

Bibliografía

• Apostol, T., Análisis Matemático (2a ed.). México: Editorial Reverté, 1996. Págs: 271 y 272.
• Clapp, M., Análisis Matemático. Ciudad de México: Editorial Papirhos, IM-UNAM, 2013. Pág: 86-88.

Enlaces

• Análisis Matemático.
• Guía de notación para Análisis Matemático I
• Enlace a entrada anterior.
• Enlace a entrada siguiente.

Introducción

Probablemente recuerdes de los cursos de ecuaciones diferenciales algunos teoremas que, bajo ciertas condiciones, aseguran que existe una solución a una ecuación diferencial y además, esta es única. Puedes observar esta teoría a detalle en la página del curso Ecuaciones Diferenciales I en las secciones correspondientes a teorema de existencia y unicidad. Aquí probaremos el teorema como una aplicación del teorema de punto fijo de Banach. Comenzaremos resolviendo una ecuación diferencial particular.

Ejemplo: $\dfrac{dy}{dx} = y,$ con condición inicial $y(0)=1.$

Considera la ecuación

$$\frac{d \, y(x)}{dx} = y(x), \, y(0)=1$$

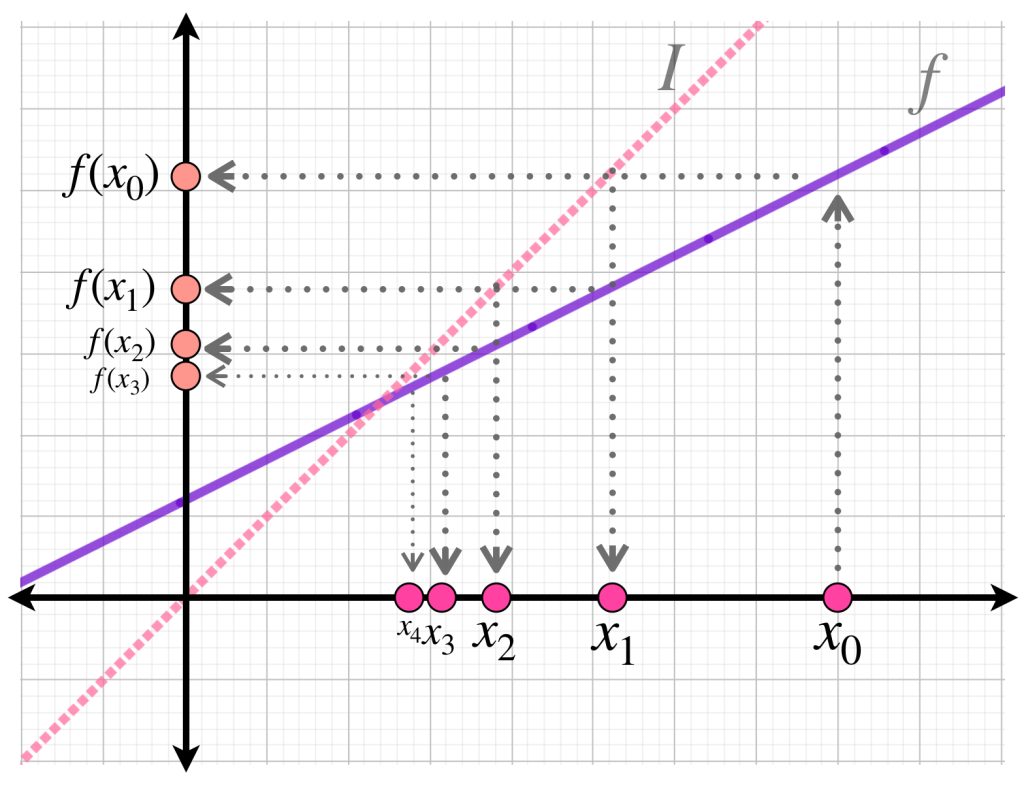
Resolverla significa encontrar una función $\, y \,$ cuya derivada respecto a la variable $x$ coincida con ella misma. Ya que buscamos llegar a que la solución existe y es única, habría que pensar en hallarla dentro de un espacio métrico completo tras aplicar varias veces, una función contracción. En estas condiciones el teorema de punto fijo de Banach asegura que la sucesión generada converge a un punto fijo que, en este caso, representa la solución de la ecuación diferencial.

Comencemos identificando la contracción $\phi$ que servirá al objetivo. Si $f$ es punto fijo de $\phi$ se tiene que

$$\phi(f) = f$$

Y si además es solución de $\dfrac{dy}{dx} = y \,$ también cumple que

$$f'(x)=f(x)$$

Esto nos lleva a buscar a $f$ en el espacio de funciones continuas $\mathcal{C}^0[a,b]$ con la métrica uniforme $d_\infty$ y con $a,b \in \mathbb{R}$ tales que $0 \in [a,b],$ pues es donde se considera la condición inicial. Recordemos que en la entrada Convergencia uniforme y continuidad vimos propiedades que permiten concluir que este espacio sea completo. Así, el espacio identificado satisface las condiciones del teorema de punto fijo de Banach.

Supón que

\begin{align*}
&& f'(x) &=f(x)\\
&\Rightarrow &\int_{0}^{x} f'(t) \, dt & = \int_{0}^{x} f(t) \, dt \\
&\Rightarrow &f(x) \, – \, f(0) &= \int_{0}^{x} f(t) \, dt \\
&\Rightarrow &f(x) &= f(0) + \int_{0}^{x} f(t) \, dt
\end{align*}

De modo que definiremos $\phi$ como

$$\phi(f(x))\ := \, f(0) + \int_{0}^{x} f(t) \, dt $$

Si buscamos que la condición inicial sea $f(0) = 1,$ tenemos:

$$\phi(f(x))\ := \, 1 + \int_{0}^{x} f(t) \, dt$$

Existe un intervalo donde $\phi$ es contracción

A continuación probaremos que existe un intervalo $[a,b] \subset \mathbb{R}$ con $0 \in [a,b]$ donde la $\phi$ definida es contracción, es decir, que para cualquier $f,g \in \mathcal{C}^0[a,b]$ ocurre que $d_\infty(\phi(f)), \phi(g)) \leq \alpha \, d_\infty (f,g),$ para algún $\alpha \in (0,1).$

Proponemos $[a,b] = [-\frac{1}{2},\frac{1}{2}].$ Tenemos dos casos:

Si $0 \leq x.$

\begin{align*}
|\phi(f(x)) \, – \, \phi(g(x))|&= \left|1 + \int_{0}^{x} f(t) \, dt \, – \, \left(1 + \int_{0}^{x} g(t) \, dt \right)\right|\\
&= \left|\int_{0}^{x} f(t) – g(t) \, dt \right|\\
& \leq \int_{0}^{x} |f(t) – g(t)| \, dt\\
& \leq (x-0) d_\infty(f,g) \\
& \leq \frac{1}{2} d_\infty(f,g)
\end{align*}

Si $x < 0.$

\begin{align*}
|\phi(f(x)) \, – \, \phi(g(x))|&= \left|1 + \int_{0}^{x} f(t) \, dt \, – \, \left(1 + \int_{0}^{x} g(t) \, dt \right)\right|\\
&= \left|\int_{0}^{x} f(t) – g(t) \, dt \right|\\
&= \left|- \int_{x}^{0} f(t) – g(t) \, dt \right|\\
&= \left| \int_{x}^{0} f(t) – g(t) \, dt \right|\\
& \leq \int_{x}^{0} |f(t) – g(t)| \, dt\\
& \leq (0-x) d_\infty(f,g) \\
& \leq \frac{1}{2} d_\infty(f,g)
\end{align*}

De ambos casos se sigue que

\begin{align*}
d_\infty(\phi(f)), \phi(g)) &= \underset{-\frac{1}{2} \leq x \leq \frac{1}{2}}{sup} \, |\phi(f(x)) \, – \, \phi(g(x))| \\
&\leq \underset{-\frac{1}{2} \leq x \leq \frac{1}{2}}{sup} \, \frac{1}{2} d_\infty(f,g) \\
& = \frac{1}{2} d_\infty(f,g)
\end{align*}

Por lo tanto $d_\infty(\phi(f),\phi(g)) \leq \frac{1}{2} \, d_\infty(f,g)$

Lo cual prueba que $\phi$ es una contracción con constante $\alpha = \frac{1}{2}.$

Nota que $[-\frac{1}{2}, \frac{1}{2}]$ cumple que tiene al punto $0,$ valor considerado condición inicial y donde se busca que $f(0)=1.$ Por otro lado, el tamaño de este intervalo, o más específicamente, la distancia entre $0$ y $\frac{1}{2}$ permite concluir la última desigualdad. Aunque la solución que vamos a encontrar satisface la ecuación en todo $\mathbb{R},$ las condiciones de este método encuentran la solución en un intervalo pequeño.

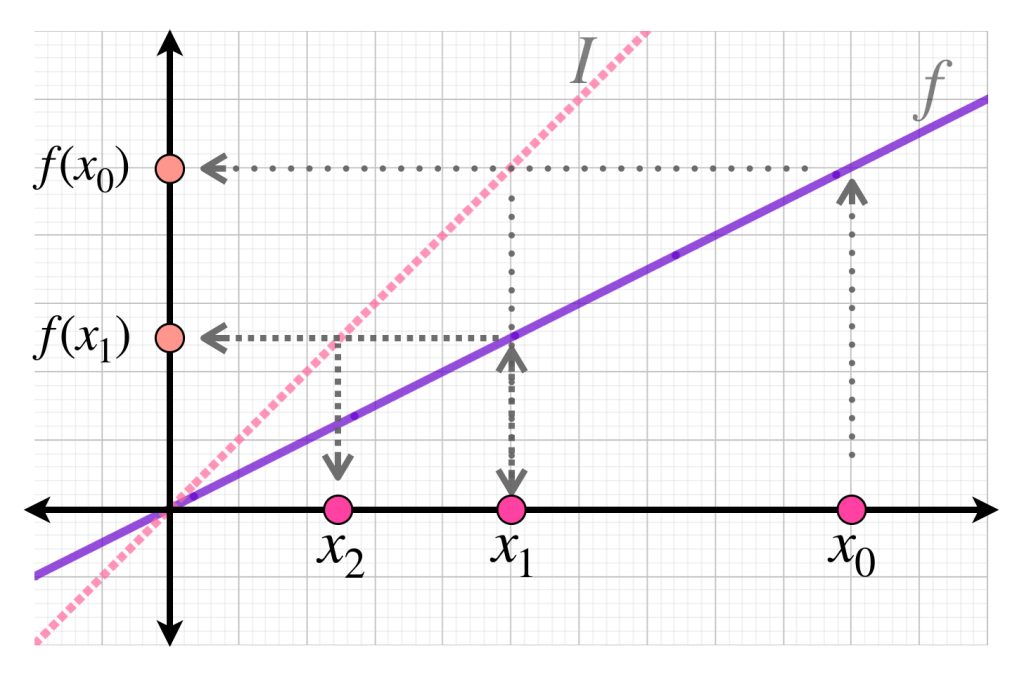
Generamos la sucesión $(\phi^n)_{n \in \mathbb{N}}$

A continuación generaremos la sucesión a partir de iteraciones en la función constante que satisface que para todo $x \in [-\frac{1}{2}, \frac{1}{2}], \, f_0(x) := 1.$ El teorema de punto fijo de Banach nos dice que esto nos permite llegar en el límite a la función buscada.

$f_0(x) = 1$
$f_1(x) = \phi(f_0(x)) = 1 + \int_{0}^{x}1 \, dt = 1+x$
$f_2(x) = \phi(f_1(x)) = 1 + \int_{0}^{x}1+t \, dt = 1+x+ \frac{x^2}{2}$
$f_3(x) = \phi(f_2(x)) = 1 + \int_{0}^{x}1+t + \frac{t^2}{2}\, dt = 1+x+ \frac{x^2}{2}+ \frac{x^3}{6}$
.
.
.
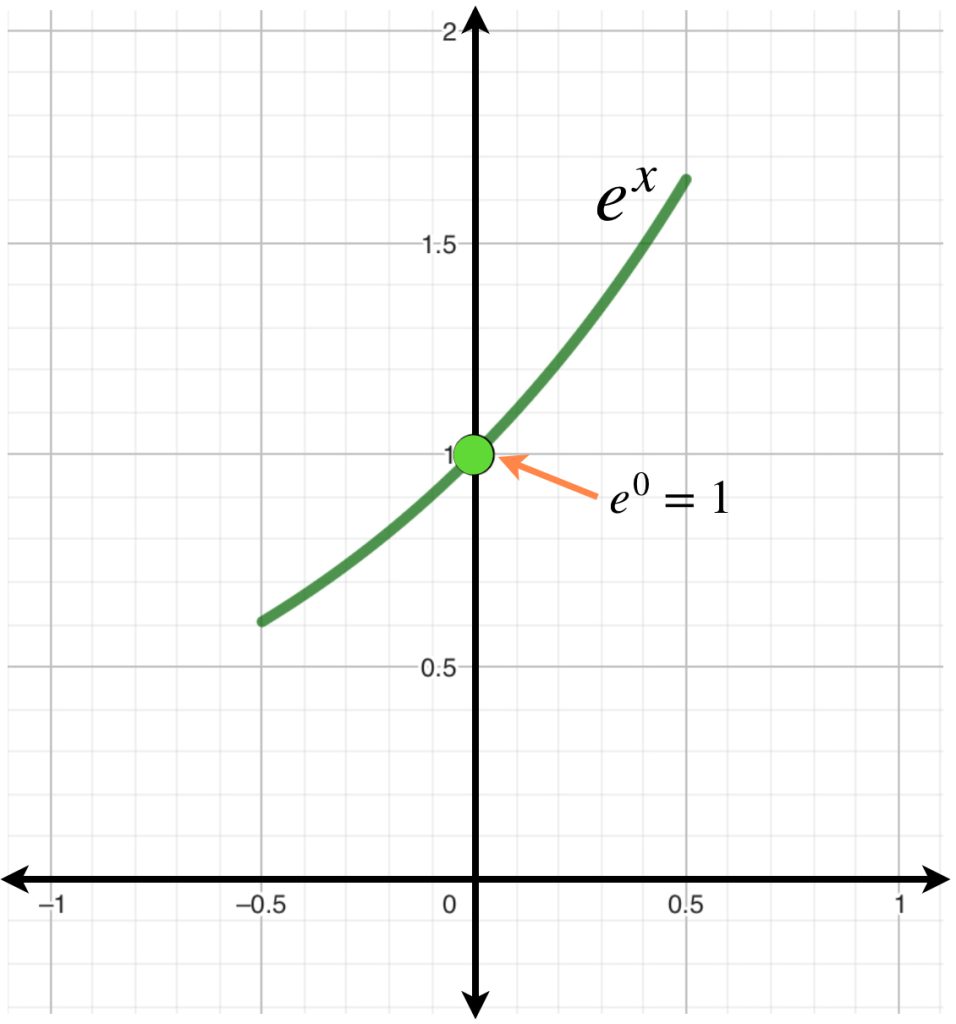
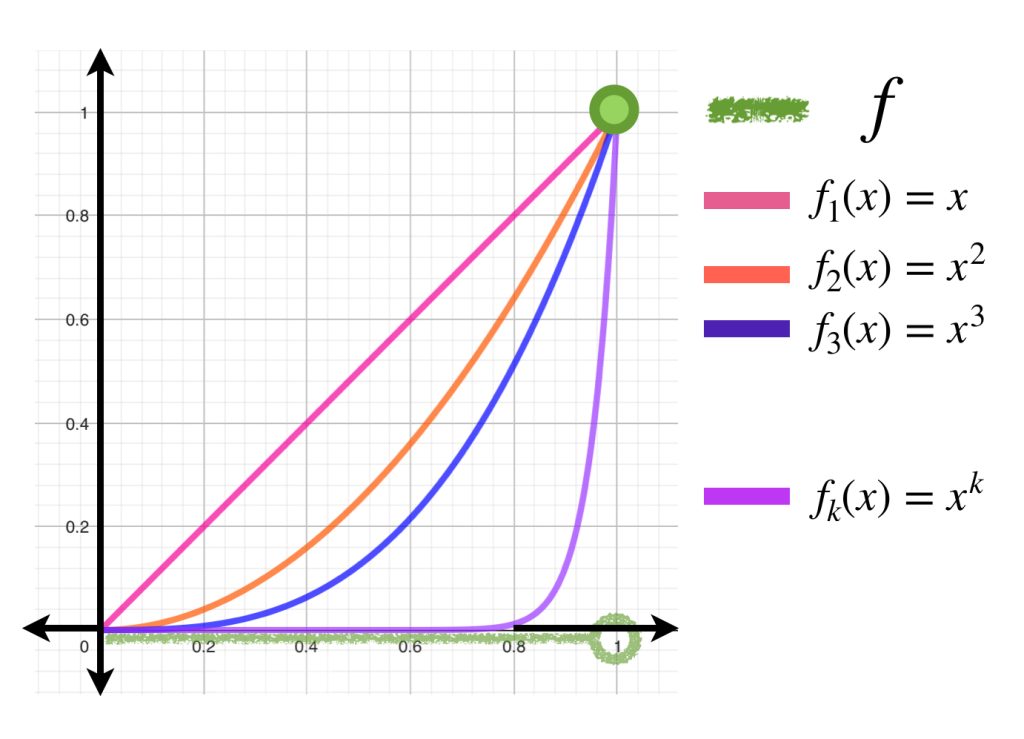
Entonces $ \, \underset{n \to \infty}{lim} \,f_n(x) \, = \, \displaystyle \sum_{k=0}^{\infty}\dfrac{x^k}{k!} = e^x.$

Queda como ejercicio al lector confirmar que $\phi(e^x)= e^x$ es decir, que $e^x$ es punto fijo de $\phi$ y que satisface la ecuación diferencial.

Más adelante…

Aplicaremos este método para resolver ecuaciones diferenciales más generales. Antes hablaremos de algunos resultados que usaremos en la prueba y veremos en la siguiente entrada.

Tarea moral

1. Evalúa $\phi(e^x)$ y confirma que es igual a $e^x.$
2. Propón otro intervalo $[a,b] \subset \mathbb{R}$ donde también funcione el método usado.
3. Resuelve la misma ecuación diferencial pero con condición inicial $y(1)=1.$

Bibliografía

Enlaces

• Análisis Matemático.
• Guía de notación para Análisis Matemático I
• Enlace a entrada anterior.
• Enlace a entrada siguiente.