Introducción

En esta entrada vamos a hablar de el principio de inducción que se deriva del quinto axioma de Peano. Veremos cómo es que nos ayudará a un nuevo tipo de demostraciones, lo que significa en términos simples y algunos ejemplos de su uso.

El efecto dominó

Pensemos un poco en cómo funciona la inducción matemática viendo un ejemplo con las fichas de dominó. Imaginamos tenemos tres fichas de domino y las paramos una detrás de otra:

Si nosotros tiramos la primera ficha, las otras dos caerán:

Lo que se necesita para que se caigan las fichas será que la primera ficha caiga. Esto es cierto bajo ciertas condiciones. Deberemos saber que las fichas están suficientemente juntas para que una tire a la otra. Si por ejemplo, la última pieza estuviera muy lejos, la segunda pieza no la tiraría:

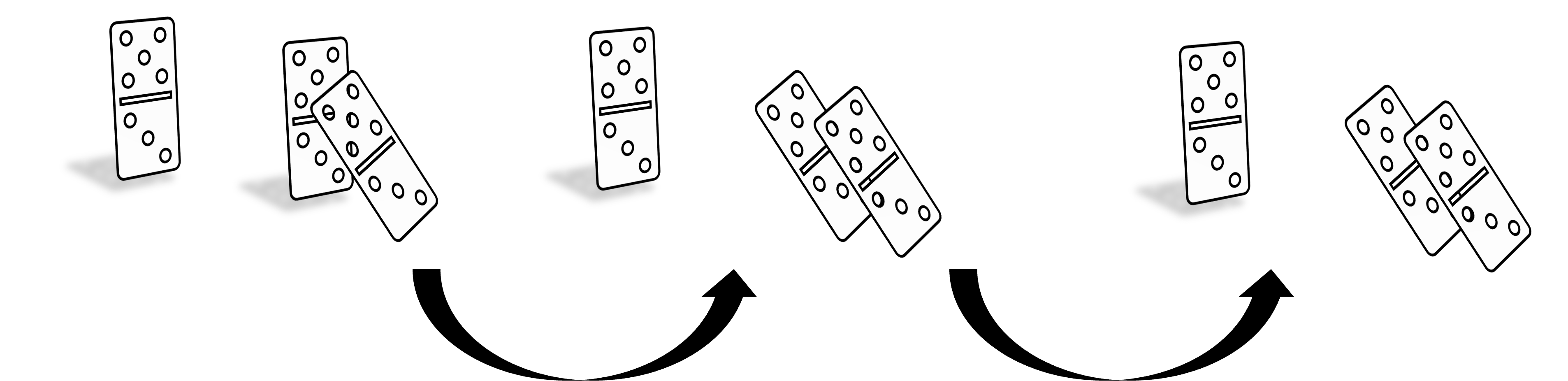
Con esto en mente, podríamos decir que todas las piezas de dominó se caen si:

1. La primera pieza se cae.
2. Cada vez que una pieza se cae, la pieza que sigue igual se cae.

Ahora, supongamos que tenemos una sucesión infinita de piezas de dominó, y enumeremos las piezas según los números naturales:

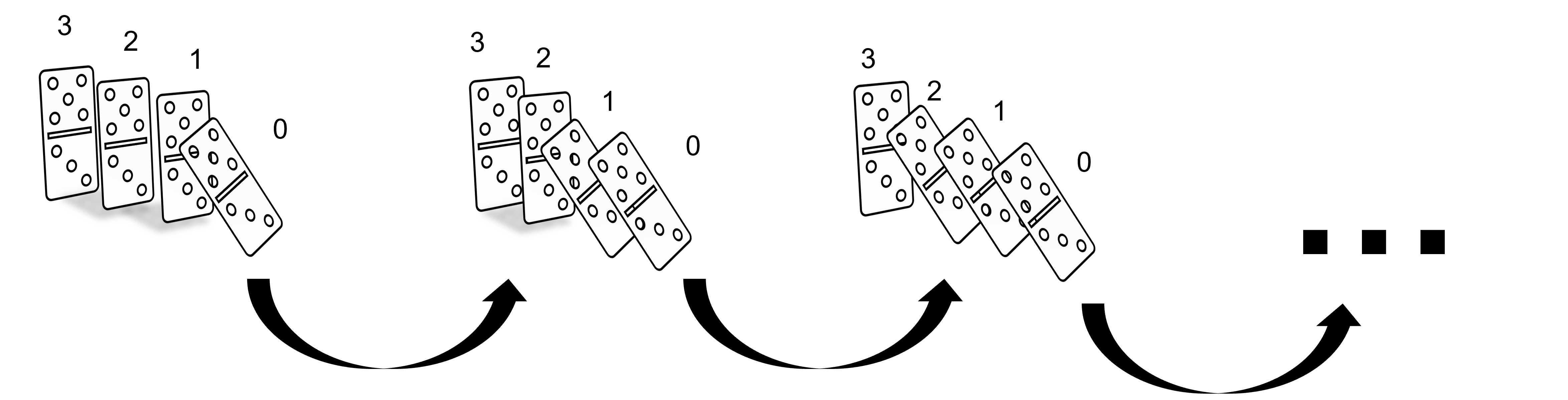
En el caso de que nuestras piezas estén bien colocadas, si tiramos la pieza $0$, esperaremos que se caiga la ficha $1$, seguido de la $2,$ la $3$ y así sucesivamente. De hecho si por algún momento dejáramos de ver las piezas y volteamos a ver en algún momento cualquier ficha cayendo, sabremos que la siguiente igual se cae. Es decir, imagina que nos distraemos después de tirar la primera ficha, al momento de volver a voltear a ver las fichas cayendo, estaremos viendo que alguna pieza se va cayendo tirando la que sigue. Digamos que nombramos a esta pieza la ficha $n$, entonces observaremos a la pieza $n+1$ caer enseguida:

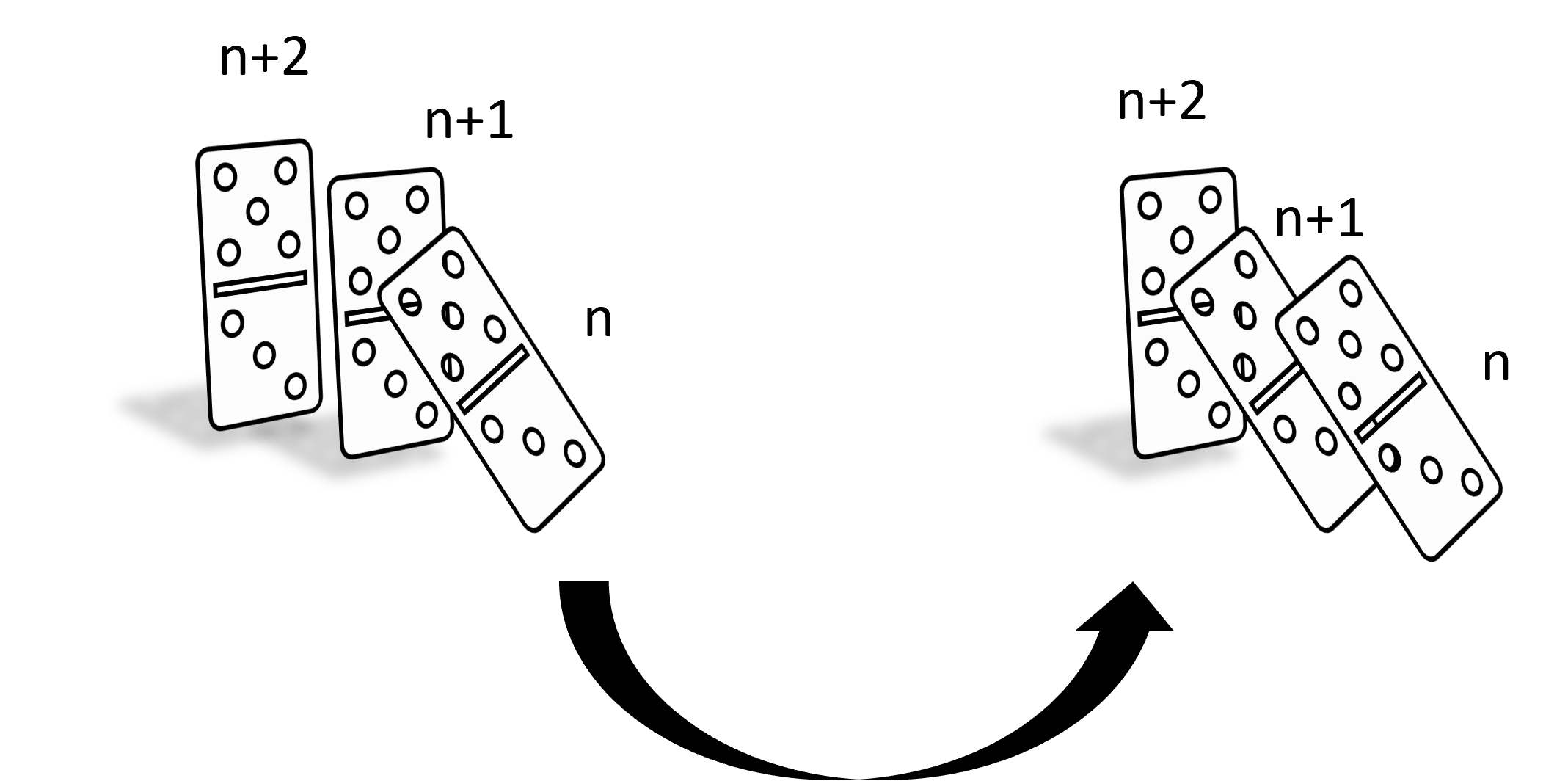
Lo que nos interesa para decir que todas las piezas se caen es que si una ficha se cae, la siguiente se cae. Es esta misma idea bajo las que se rige la inducción matemática, veamos la parte matemática de esta idea.

Sobre el quinto axioma de Peano

Veamos qué nos dice el último axioma que definimos con anterioridad:

Axioma 5 (Primer principio de inducción). Si $S$ es un subconjunto de $ \mathbb{N} $ tal que:

1. $0 \in \mathbb{N}$
2. Para cada número $n \in S$, sucede que $\sigma(n) \in S$

Entonces $S=\mathbb{N}$

Y veamos cómo es que esto se une con lo que hemos dicho sobre las fichas de dominó. La primera condición la podemos traducir como

1.Se cae la primera pieza.

Mientras que la segunda condición del axioma nos diría que:

2. Siempre que se cae una ficha, se cae la ficha que se encuentra delante.

Finalmente si se cumplen estas dos condiciones, nuestro axioma nos diría que el conjunto $S$ es el conjunto de los números naturales, pero recordemos que esto en términos del dominó significa que todas las piezas se caen. Entonces lo que nos dice el quinto axioma es que para verificar que un conjunto de números naturales es de hecho el conjunto de los números naturales, deberemos de ver que el primer número natural está y cada vez que veamos que un número natural está en el conjunto, su sucesor también deberá estar. La razón por la que intuitivamente esto funciona es por el principio del dominó.

Cuando nosotros tenemos una proposición matemática $P(n)$ para la cual queremos comprobar que cualquier número natural $n$ la cumple, la técnica de demostración por inducción será útil porque en lugar de probar que cada número individualmente la cumple, bastará demostrar que se satisfacen las condiciones del principio de inducción para argumentar que todos los números naturales la cumplen.

Algoritmo de demostraciones por inducción

Supongamos tenemos una proposición en el conjunto de los números naturales $P(n)$. El segundo axioma de los conjuntos garantiza la existencia de un conjunto 
$$S = \{n: P(n)\}$$.
Y el axioma 5 de Peano argumenta que si se cumplen las siguientes dos condiciones:

1. El $0$ pertenece al conjunto $S$ 
2. Si $n \in S$ entonces $n+1 \in X$

entonces $S = \mathbb{N}$. Es decir, todos los números naturales cumplen la condición $P(n)$
Veamos ahora estos dos pasos uno por uno:
1. Base inductiva: Probar que se cae la primera ficha. Este paso consistirá en demostrar que se cumple $P(0)$
2. Hipótesis de inducción: Suponer que un número $n$ cumple $P(n)$
3. Paso inductivo: Demostrar que la siguiente ficha se cae. En este paso debemos demostrar que se cumple también $P(n+1)$

Un ejemplo de inducción matemática

Proposición. La suma de los primeros $n$ números naturales es $\frac{n(n+1)}{2}$.

Esta proposición nos dice que si sumamos los primeros $n$ números n, el resultado será: $$ \sum_{i=0}^{n} i = 0+1+2+\dots+n-1+n = \frac{n(n+1)}{2}.$$ Para demostrar esto, seguiremos los pasos del algoritmo. Para ello, consideremos al conjunto $S=\{n \in \mathbb{N}: \sum_{i=0}^{n} i = \frac{n(n+1)}{2} \}$, es decir, $S$ es el conjunto de los números naturales $n$ para los cuales la suma de los primeros $n$ números naturales equivale a $ \frac{n(n+1)}{2} $. Lo que queremos demostrar es que este conjunto $S$ son todos los números naturales, es decir, que todos los números naturales cumplen esta condición. Para ello seguiremos los pasos del algoritmo.

Demostración. (por inducción sobre $n$).

Base inductiva. Demostraremos que $ \sum_{i=0}^{0} i = \frac{0(0+1)}{2} $. En efecto, notemos que $$ \sum_{i=0}^{0} i = 0= \frac{0(0+1)}{2} .$$ Así, ha quedado demostrada la base inductiva.

Hipótesis de inducción. Supongamos que $n \in \mathbb{N}$ es tal que $ \sum_{i=0}^{n} i = \frac{n(n+1)}{2} $.

Paso inductivo. Ahora demostraremos que $$ \sum_{i=0}^{n+1} i = \frac{(n+1)((n+1)+1)}{2}. $$ Para ello, basta notar que
$$\begin{align*}
\sum_{i=0}^{n+1} i &= \sum_{i=0}^{n} i + n+1 \\
&= \frac{n(n+1)}{2} + n+1 (\text{ esto por hipótesis de inducción}) \\
&= \frac{n(n+1)}{2} + \frac{2n+2}{2} \\
&= \frac{n(n+1)+2n+2}{2} \\
&= \frac{(n^2+n)+2n+2)}{2} \\
&= \frac{n^2+3n+2)}{2} \\
&= \frac{(n+1)(n+2)}{2} = \frac{(n+1)((n+1)+1)}{2} .
\end{align*}$$Quedando así demostrado el paso inductivo.

Así, hemos demostrado que el conjunto $S=\mathbb{N}$, es decir, que se cumple para todos los números naturales, quedando demostrada la proposición.

$\square$

Más adelante…

En la siguiente entrada daremos la definición de funciones recursivas que serán en pocas palabras, funciones en los números naturales las cuales son funciones que podemos definir solo diciendo cuánto valen en el $0$ y la evaluación en un término $\sigma(k)$ depende únicamente de la evaluación en $k$. También daremos un vistazo general al teorema de recursión.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Demuestra por inducción que la suma de los primeros $n$ números pares es $n(n+1)$.
2. Encuentra una fórmula para la suma de los primeros $n$ números impares usando el ejercicio anterior junto al ejemplo demostrado en la entrada.
3. Prueba que para cualquier número natural $n$, $$\sum_{i=1}^n(2i-1) = n^2 $$.

Entradas relacionadas

• Ir a Álgebra Superior I
• Entrada anterior del curso: Introducción a números naturales
• Siguiente entrada del curso: Problemas de inducción

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»