Introducción
Esta entrada es parte de una serie de notas introductorias sobre técnicas de demostración. En esta entrada se habla sobre demostraciones de proposiciones con conectores. Cada entrada está ligeramente relacionada con las otras. Para entenderlas bien, usamos el siguiente diagrama que recopila cómo se comporta un mundo fantástico llamado Axios, en donde habitan creaturas llamadas Blorgs. Para leer más sobre ello, haz click aquí.
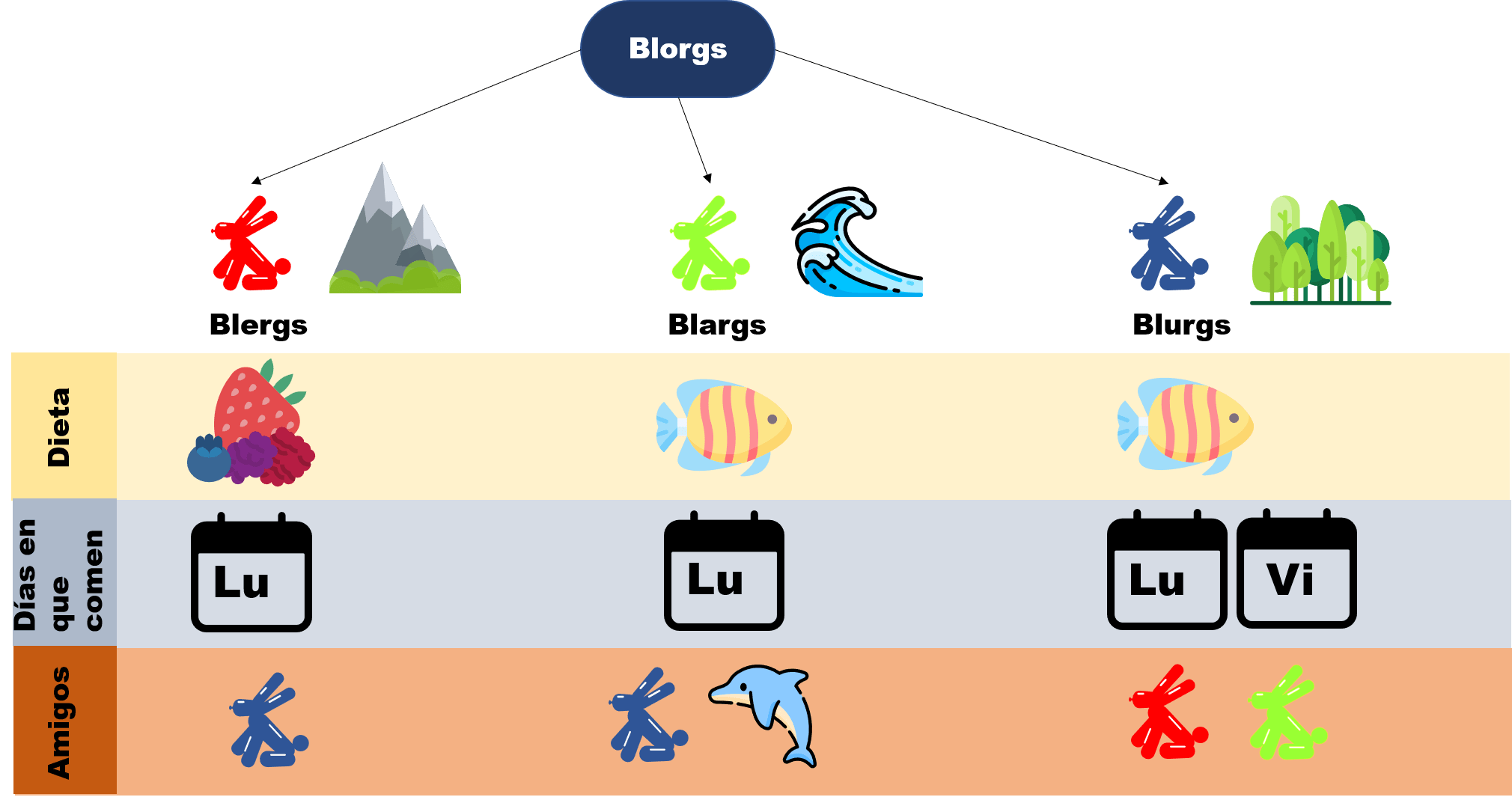
Hasta ahora hemos visto varias estrategias para demostrar: demostaciones directas, demostraciones indirectas y por contradicción. Ahora pensaremos en cómo realizar demostraciones de ciertas afirmaciones cuando hay conectores tanto en nuestras premisas, como en las conclusiones que queremos obtener. Veremos cómo es que se piensa al hacer estas demostraciones y algunas consideraciones que debemos tomar en cuenta.
Recordando conectores
Como breve recordatorio, tenemos los siguientes conectores lógicos:
- Conjunción $P\land Q$, que es cierta si ambos $P$ y $Q$ lo son.
- Disyunción $P\lor Q$, que es cierta si alguno de $P$ o $Q$ lo son.
- Implicación $P\Rightarrow Q$, que es cierta si bien $P$ es falsa, o si $P$ y $Q$ son verdaderas simultáneamente.
- Doble implicación $P\Leftrightarrow Q$, que es cierta si $P$ y $Q$ tienen el mismo valor de verdad.
En esta entrada veremos qué hacer con las demostraciones que tienen conjunciones y disyunciones. Más adelante hablaremos de las implicaciones y las dobles implicaciones. Los conectores lógicos pueden aparecer como las hipóteis, o como la conclusión de algo que queremos demostrar. Para realizar estas demostraciones, tomaremos en cuenta lo siguente.
- Si una conjunción $P\land Q$ aparece como hipótesis, entonces podemos suponer tanto que $P$ como $Q$ son verdad.
- Si una conjunción $P\land Q$ aparece como conclusión, entonces debemos mostrar, quizás por separado, que cada una de $P$ y $Q$ se siguen de las premisas.
- Si una disyunción $P\lor Q$ aparece como hipótesis, sólo sabemos que $P\lor Q$ es cierta, no tenemos la garantía de que ninguna de ellas en específico sea cierta, solo que alguna lo es. Por ello, debemos separar en casos nuestra demostración, y argumentar por qué la conclusion se sigue tanto cuando $P$ es cierta, como cuando $Q$ es cierta. Esto típicamente llevará a dos o más subdemostraciones.
- Si una disyunción $P\lor Q$ aparece como conclusión, entonces basta probar a partir de las hipótesis alguna de $P$ o $Q$, la que nos parezca más fácil, para concluir la demostración.
Ejemplos de demostraciones con conjunciones y disyunciones
Veamos algunos ejemplos.
Proposición: Si un Blorg es un Blarg o es un Blurg, entonces come peces.
Demostración: Aquí la disyunción está en la hipótesis. Un Blorg $x$ que cumple la hipótesis cumple que «$x$ es Blarg o $x$ es Blurg». Como no tenemos certeza de cuál de las proposiciones es cierta, debemos hacer casos.
- Si $x$ es Blarg, entonces uno de los axiomas nos dice que $x$ come peces.
- Si $x$ es Blurg, entonces otro de los axiomas nos dice que $x$ come peces.
En cualquier caso, concluimos que $x$ come peces.
$\square$
Veamos un ejemplo de la conjunción en la hipótesis.
Proposición. Si un Blorg que come en peces y es amigo de los delfines, entonces es un Blarg.
Demostración. Tomemos $x$ un Blorg que come peces y es amigo de los delfines. Entonces podemos usar la información de ambas proposiciones en la demostración. Como $x$ come peces, entonces $x$ es Blarg o $x$ es Blurg. Como tenemos una disyunción, hay dos posibilidades: que $x$ es Blarg o que $x$ es Blurg. Veremos que $x$ es Blarg. Para ello, procedemos por contradicción, y suponemos que $x$ no es Blarg. Como «$x$ es Blarg o $x$ es Blurg», entonces $x$ es Blurg. Pero entonces $x$ es Blurg y es amigo de los defines. Pero uno de los axiomas es que los Blurg son amigos sólo de los Blergs y los Blargs. ¡Esto es una contradicción! Así, el problema fue suponer que $x$ no es Blarg. Por lo tanto $x$ es Blarg.
$\square$
Veamos un ejemplo más, con una mezcla de conectores.
Proposición. Si un Blorg es Blerg o es Blarg, entonces come los lunes y es amigo de los Blurgs.
Demostración. Otra vez, en la hipótesis tenemos una disyunción. Tomemos un Blorg $x$ que cumple la hipótesis. Entonces «$x$ es Blerg o $x$ es Blarg». Se tienen que hacer casos.
- Si $x$ es Blerg, entonces como axioma tenemos que $x$ come los lunes. También como axioma tenemos que $x$ es amigo de los Blurgs. Así, tenemos que «$x$ come los lunes y es amigo de los Blurgs.»
- Si $x$ es Blarg, entonces como axioma tenemos que $x$ come los lunes. También como axioma tenemos que $x$ es amigo de los Blurgs. Así, tenemos que «$x$ come los lunes y es amigo de los Blurgs.»
En cualquier caso, ya mostramos las dos partes que conforman la conjunción de la conclusión. Por lo tanto, en cualquier caso $x$ come los lunes y es amigo de los Blurgs, como queríamos.
$\square$
Hagamos una demostración más.
Proposición: Los Blargs comen animales marinos y comen entre semana.
Demostración: Para probar la proposición, será necesario probar dos cosas: Que los Blargs comen animales marinos, y que los Blargs comen entre semana, es decir que no comen el fin de semana.
Ahora notemos que todos los Blargs comen peces, y estos son animales marinos, entonces se cumple la afirmación de que los Blargs comen animales marinos.
Como es una conjunción, ahora tenemos también que demostrar que comen entre semana. Para esto, recuerda que cada Blarg come los lunes, y como podrás imaginar, esto significa que comen entre semana, por lo que ya demostramos que «Los Blargs comen animales marinos y comen entre semana».
$\square$
Conectando conectores
Ahora podemos ir más allá y hacer otras combinaciones de conectores. Aunque al inicio parezca que se tienen enunciados complicados, basta con pensar la proposición en cada uno de sus componentes para pensar qué hacer.
Proposición: Si un Blorg no es verde, entonces come algún día entre jueves y domingo, o tiene amigos de color azul.
Antes de continuar con la demostración, vamos a desmenuzar la oración en sus partes escribiéndola con lógica proposicional. Si consideramos:
$ P(x): x$ no es verde,
$ Q(x): x$ come algún día entre jueves y domingo,
$ R(x): x$ tiene amigos de color azul,
entonces la proposición es de la forma
$\forall x (P(x) \Rightarrow (Q(x) \lor R(x))).$
De esta forma ya tenemos un poco más claro qué queremos demostrar. Empezaremos con un Blorg $x$ para el cual la proposición $P(x)$ sea válida y demostraremos que sucede $Q(x)$ o sucede $R(x)$.
Demostración: Sea $x$ un Blorg que no es verde. Esto significa que no es un Blarg, entonces tenemos dos casos:
Caso 1: $x$ es un Blerg.
Si $x$ es un Blerg, entonces es amigo de los Blurgs. Y como recordarás, los Blurgs son azules, de esta manera se cumple la proposición.
Caso 2: $x$ es un Blurg.
Si nuestro Blorg es un Blurg, entonces come los viernes, que resulta que son un día entre jueves y domingo. De esta manera la proposición también se cumple.
En cualquiera de los casos, la proposición es válida.
$\square$
Más adelante…
Ya hemos recorrido algunas de las formas de demostraciones que te encontrarás a lo largo de tu viaje matemático. Sin embargo aún hay algunas cosas que conviene que platiquemos. ¿Cómo demostramos proposiciones en las que están involucrados condicionales y cuantificadores? En la siguiente entrada comenzaremos con el caso de los cuantificadores y posteriormente hablaremos sobre los condicionales.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Prueba que «Para cualquier Blorg $x$, si $x$ no es rojo y $x$ no es amigo de los delfines, entonces $x$ come los viernes».
- Prueba que «Para cualquier Blorg $x$, o bien $x$ es verde, o bien $x$ es amarillo, o bien $x$ es azul».
- Prueba que «Para cualquier Blorg $x$, o bien $x$ es amigo de los animales marinos, o bien $x$ come los viernes, o bien $x$ es rojo».
- Escribe con lógica proposicional la proposición: «Si un Blorg come los viernes entonces en su hábitat hay árboles y come animales marinos».
- Demuestra que «Si un Blorg come los viernes entonces en su hábitat hay árboles y come animales marinos».
Entradas relacionadas
- Ir a Álgebra Superior I
- Entrada anterior del curso: Problemas introductorios a demostraciones
- Siguiente entrada del curso: Demostración de proposiciones con cuantificadores
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»
