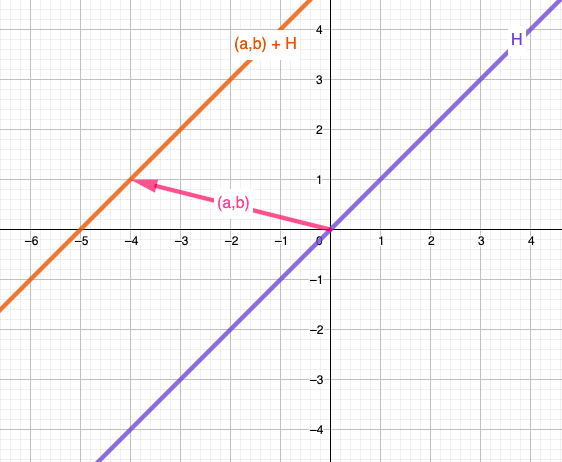(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Antes de comenzar conviene que recordemos que estamos trabajando con grupos. Un conjunto con una operación da lugar a un grupo si cumple ciertas condiciones, entre ellas tener un neutro y ser cerrado bajo su operación. Ahora nos interesamos por los subconjuntos cualquiera del grupo, no necesariamente subgrupos. Esta entrada está dedicada al estudio del producto de dichos subconjuntos.

La primera parte comienza definiendo a nuestro producto y lo ilustramos con unos ejemplos. La segunda parte pretende responder a la pregunta ¿cuándo es el producto de dos subconjuntos un subgrupo? En la tercera parte, nos imaginamos un caso particular, ¿qué pasa cuando uno de los subconjuntos elegidos es unitario? Es decir, estamos multiplicando un subgrupo de $G$ por un solo elemento de $G$.

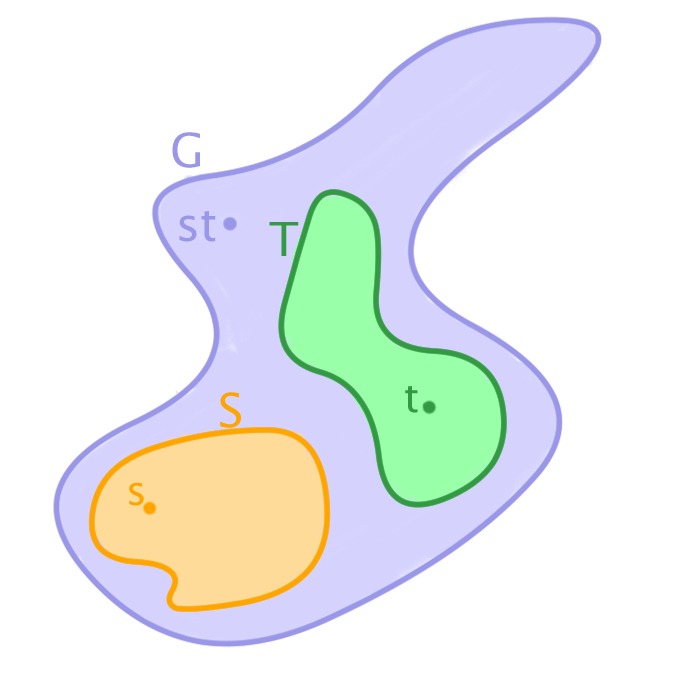
Producto de $S$ con $T$

Ejemplos.

1. Tomemos las permutaciones de $S_3 = \{(1), (1\;2), (1 \;3), (2 \; 3), (1 \; 2 \; 3), (1\;3\;2)\}$. Consideramos a $S$ como $S=\{(1\;2)\}$ y a $T$ como $T=\{(1\;2\;3), (1\;3\;2)\}$. Entonces, su producto queda
   \begin{align*}
   ST &= \{(1\;2) (1\;2\;3), (1\;2)(1\;3\;2)\}\\
   &= \{(2\;3), (1\;3)\}.
   \end{align*}
2. Si consideramos $(\z, +)$, podemos tomar a $S$ y a $T$ como
   \begin{align*}
   S &= 2\z = \{2n|n\in \z\},\\
   T &= 3\z = \{3m|m\in\z\}.
   \end{align*}
   En este caso, el producto se denota como $S+T$ y este conjunto es
   \begin{align*}
   S+T = 2\z + 3\z = \{2n+3m|n,m\in\z\} = \z.
   \end{align*}
   Donde la última igualdad se da porque $(2,3) = 1$ (es decir, $2$ y $3$ son primos relativos).

¿Cuándo es el producto un subgrupo de $G$?

Vamos a ver qué pasa ahora a la hora de multiplicar subgrupos. Durante la demostración del siguiente teorema, observaremos que en general, el producto no es un subgrupo debido a un detalle de la conmutatividad de los elementos. El siguiente se trata de un resultado clásico que aparece por ejemplo en el texto de Dummit mencionado en la bibliografía, Proposición 14:

Teorema. Sea $G$ un grupo, $H$, $K$ subgrupos de $G$. Entonces,
\begin{align*}
HK \leq G \; \text{ si y sólo si } \; HK = KH.
\end{align*}

Demostración.
Sea $G$ un grupo, $H,K$ subgrupos de $G$.

$|\Rightarrow)$ Supongamos que $HK \leq G$.
P.D. $KH=HK$

Procedemos por doble contención.
$\subseteq]$
Sea $x\in KH$, entonces existen $k \in K$ y $h \in H$ tales que $x = kh$.

Como $HK$ es subgrupo de $G$, entonces $h^{-1}k^{-1} \in HK$, así
\begin{align*}
x^{-1} = (kh)^{-1} = h^{-1}k^{-1} \in HK.
\end{align*}

Entonces, $x^{-1} \in HK$, y como $HK$ es subgrupo, $x \in HK$. Por lo tanto $KH \subseteq HK$.

$\supseteq]$
Sea $x \in HK$.

Observación: Si intentamos hacer lo mismo de antes, tomaríamos $h \in H$ y $k \in K$ tales que $x = hk$, así $x^{-1} = k^{-1}h^{-1}$ ya que en el inverso se invierte el orden, es decir $x^{-1} \in KH$. Pero como no sabemos nada de $KH$, nos atoramos aquí. Por lo tanto, tomaremos un camino un tanto diferente.

Sabemos que $HK\leq G$, entonces sabemos que $x^{-1} \in HK$. Entonces existen $h \in H$ y $k\in K$ tales que $x^{-1}=hk$. Así,

\begin{align*}
&x = (x^{-1})^{-1} = (hk)^{-1} = k^{-1}h^{-1} \in KH
\end{align*}
Por lo tanto $HK \subseteq KH$.

Así, $HK = KH$.

$\Leftarrow|)$ Supongamos que $HK = KH$.
P.D. $HK \leq G$.

Observemos primero que $e = ee \in HK$.

Ahora consideremos $x,y \in HK$, entonces
\begin{align*}
x = hk && h, \overline{h} \in H \\
y = \bar{h} \bar{k} && k,\overline{k} \in K.
\end{align*}

Entonces
\begin{align*}
xy^{-1} = (hk)(\bar{h} \bar{k})^{-1} &= (hk)(\bar{k}^{-1} \bar{h}^{-1})\\
&= h \left( (k\bar{k}^{-1})\bar{h}^{-1} \right).
\end{align*}

Pero
\begin{align*}
&(k\bar{k}^{-1}) \bar{h}^{-1} \in KH = HK &\text{Por la hipótesis} \\
\Rightarrow &\,(k \bar{k}^{-1})\bar{h}^{-1} =\hat{h}\hat{k} & \text{ con } \hat{h}\in H,\hat{k}\in K.
\end{align*}

Sustituyendo los valores $$xy^{-1} = h(\hat{h}\hat{k}) = (h\hat{h})\hat{k} \in HK.$$

Por lo tanto $HK \leq G$.

$\blacksquare$

Del teorema anterior se sigue este corolario:

Corolario. Sea $G$ un grupo abeliano, $H,K$ subgrupos de $G$. Tenemos que $HK$ es un subgrupo de $G$.

Clases Laterales

Ahora, tomemos $T = \{a\}$ con $a \in G$. De esta manera $TH = \{a\}H$, pero para simplificar la notación, usaremos $\{a\}H = aH$. A este caso específico, lo llamaremos clase lateral. A continuación lo definiremos de una manera más formal.

Definición. Sean $G$ un grupo, $H$ un subgrupo de $G$, $a\in G$.
La clase lateral izquierda de $H$ en $G$ con representante $a$ es
$$ aH = \{ah | h\in H\}. $$
La clase lateral derecha de $H$ en $G$ con representante $a$ es
$$Ha = \{ha|h\in H\}.$$

Ambas clases son análogas, aunque como veremos más adelante no necesariamente iguales, y para fines prácticos trabajaremos sólo con una, pero es importante definir ambas.

Ejemplos.

Tarea moral

1. Prueba o da un contraejemplo: Si $G$ es un grupo y $S$ y $T$ son subconjuntos de $G$ tales que $ST$ es un subgrupo de $G$, entonces $S$ y $T$ son subgrupos de $G$.
2. Sea $D_{2(6)} = \{\text{id}, a, \dots, a^5, b, ab, \dots, a^5b \}$ el grupo diédrico formado por las simetrías de un hexágono, con $a$ la rotación de $\frac{\pi}{3}$ y $b$ la reflexión con respecto al eje $x$. Calcula las clases laterales izquierdas y derechas de $\left< a \right>$ en $D_{2(6)}$.
3. En cada inciso calcula $HK$ y determina si es un subgrupo de $S_4$.
   1. $H = \{(1), (1\;2)\}$ y $K = \{(1), (1\;3)\}$.
   2. $H = \{(1), (1\;2)\}$ y $K = \{(1), (3\;4)\}$.

Más adelante…

En la siguiente entrada definiremos una relación de equivalencia y, al tratar de describir las clases de equivalencias inducidas, podremos relacionar las clases laterales con los elementos de $H$. Además, continuaremos respondiendo a las preguntas: ¿qué relación existe entre el número de elementos de las clases laterales derechas e izquierdas? y ¿qué es el índice de $H$ en $G$?

Entradas relacionadas

• Ir a Álgebra Moderna I.
• Entrada anterior del curso: Paridad de una permutación.
• Siguiente entrada del curso: Relación de equivalencia dada por un subgrupo e índice de $H$ en $G$.
• Resto de cursos: Cursos.