Introducción

En esta entrada daremos algunas definiciones básicas sobre series de números complejos, así como algunos resultados importantes sobre la convergencia de dichas series, por lo que se recomienda revisar los resultados sobre sucesiones de números complejos vistos en la entrada 8 de la primera unidad.

Los resultados de esta entrada serán de utilidad al trabajar con series de funciones y series de potencias en las siguientes entradas.

Definición 27.1. (Serie de números complejos.)
Sea $\left\{z_n\right\}_{n\in\mathbb{N}} \subset\mathbb{C}$ una sucesión de números complejos. Una serie infinita de números complejos o simplemente una serie de números complejos es una expresión de la forma: \begin{equation*} \sum_{n=0}^\infty z_n, \end{equation*} donde $z_n$ es llamado el $(n+1)$-ésimo término de la serie.

Definimos a la sucesión de sumas parciales $\left\{s_n\right\}_{n\geq 0}$ como: \begin{equation*} s_n = \sum_{k=0}^n z_k = z_0 + z_1 + \cdots + z_n. \end{equation*}

Notemos que a cada serie de números complejos $\sum_{n=0}^\infty z_n$ le podemos asociar una sucesión de sumas parciales $\left\{s_n\right\}{n\geq 0}$.

Observación 27.1.
En la entrada 8 trabajamos con sucesiones cuyo subíndice tomaba valores en $\mathbb{N}^+$, sin embargo, en el caso de las series de números complejos muchas ocasiones será conveniente trabajar con $\mathbb{N}$ (o subconjuntos de este conjunto) como conjunto de índices, es decir, podremos tener series que inicien desde distintos índices como: \begin{equation*} \sum_{n=0}^\infty z_n, \quad \sum_{n=1}^\infty z_n, \quad \sum_{n=2}^\infty z_n, \quad \ldots,\,\,\text{etc.} \end{equation*}

Por lo que, de manera indistinta trabajaremos con estos conjuntos de índices según sea conveniente.

Definición 27.2. (Serie de números complejos convergente.)
Diremos que una serie de números complejos $\sum_{n=0}^\infty z_n$ converge, o es convergente, a un número complejo $s$, si la sucesión de sumas parciales $\left\{s_n\right\}_{n\geq 0}$ converge a $s$, es decir si para todo $\varepsilon>0$ existe $N\in\mathbb{N}$ tal que si $n\geq N$, entonces: \begin{equation*}
\left|s_n – s\right| = \left|\sum_{k=0}^n z_k – s\right| < \varepsilon,
\end{equation*} lo cual denotamos como $s = \lim\limits_{n\to \infty} s_n = \sum_{n=0}^\infty z_n$. Si la sucesión de sumas parciales no converge o diverge a infinito, diremos que la serie $\sum_{n=0}^\infty z_n$ diverge o es divergente.

Observación 27.2.
De acuerdo con la definición anterior, debe ser claro que para el estudio de la convergencia de una serie de números complejos, así como de sus propiedades, utilizaremos los resultados de la entrada 8.

Proposición 27.1. (Criterio de convergencia de Cauchy para series).
Una serie de números complejos $\sum_{n=0}^\infty z_n$ es convergentes si y solo si para todo $\varepsilon>0$ existe $N = N(\varepsilon)\in\mathbb{N}$ tal que si $n, m \geq N$, con $n>m$, entonces:
\begin{equation*}
\left|\sum_{k=m+1}^n z_k \right| < \varepsilon.
\end{equation*}

Demostración. Sea $\left\{s_n\right\}_{n\geq 0}$ la sucesión de sumas parciales de la serie $\sum_{n=0}^\infty z_n$.

Notemos que para $n,m\in\mathbb{N}$, con $n>m$, tenemos que:
\begin{equation*}
\sum_{k=m+1}^n z_k = \sum_{k=0}^n z_k -\sum_{k=0}^m z_k = s_n – s_m.
\end{equation*}

$\Longrightarrow)$

Sea $\varepsilon>0$. Supongamos que $\sum_{n=0}^\infty z_n$ es convergente, entonces la sucesión $\left\{s_n\right\}_{n\geq 0}$ converge, por lo que es una sucesión de Cauchy, proposición 8.4, es decir, para el $\varepsilon>0$ dado existe $N\in\mathbb{N}$ tal que si $n,m\geq N$, con $n>m$, entonces:
\begin{equation*}
|s_n – s_m|<\varepsilon.
\end{equation*} Por lo que:
\begin{equation*}
\left|\sum_{k=m+1}^n z_k \right| = \left| s_n – s_m\right| < \varepsilon.
\end{equation*}

$(\Longleftarrow$

Sea $\varepsilon>0$, entonces existe $N(\varepsilon)\in\mathbb{N}$ tal que si $n, m \geq N$, con $n>m$, se cumple que:
\begin{equation*}
|s_n – s_m| = \left|\sum_{k=m+1}^n z_k \right| < \varepsilon.
\end{equation*}

Por lo que, la sucesión de sumas parciales $\left\{s_n\right\}_{n\geq 0}$ es de Cauchy. Como $\mathbb{C}$ es completo, proposición 8.5, entonces la sucesión $\left\{s_n\right\}_{n\geq 0}$ es convergente, por lo que $\sum_{n=0}^\infty z_n$ converge.

$\blacksquare$

Corolario 27.1. (Criterio de divergencia de una serie.)
Si una serie de números complejos $\sum_{n=0}^\infty z_n$ converge, entonces $\lim\limits_{n\to\infty} z_n = 0$, es decir la sucesión de números complejos $\left\{z_n\right\}_{n\geq 0}$ converge a $0$.

Demostración. Dadas las hipótesis, sea $\varepsilon>0$.

De la proposición 27.1 se sigue que existe $N\in\mathbb{N}$ tal que si $n,n-1\geq N$, entonces:

\begin{equation*}
|z_n – 0| = |z_n| = |s_n – s_{n-1}| = \left|\sum_{k=n}^n z_k \right|<\varepsilon,
\end{equation*} es decir $\lim\limits_{n\to\infty} z_n = 0$.

$\blacksquare$

Observación 27.3.
La utilidad de este corolario es mucha, pues nos permite tener un primer criterio de divergencia al considerar su contrapuesta, es decir si $\lim\limits_{n\to\infty} z_n \neq 0$ ó $\lim\limits_{n\to\infty} z_n = \infty$, entonces $\sum_{n=0}^\infty z_n$ diverge.

Ejemplo 27.1.
Veamos que la serie $\sum_{n=0}^\infty \left(1+i\right)^n$ es divergente.

Solución. Sea $z_n = \left(1+i\right)^n$ el $(n+1)$-ésimo término de la serie. Notemos que:
\begin{equation*}
\lim_{n\to \infty} |z_n| = \lim_{n\to \infty} |\left(1+i\right)^n| = \lim_{n\to \infty} |1+i|^n = \lim_{n\to \infty} \left(\sqrt{2}\right)^n = \infty.
\end{equation*} Por lo que, de acuerdo con el ejercicio 6 de la entrada 8, $\lim_{n\to \infty} z_n \neq 0$. Entonces la serie diverge.

Notemos que el recíproco del corolario 27.1 no es válido, es decir, la condición $\lim\limits_{n\to\infty} z_n = 0$ no es suficiente para garantizar la convergencia de una serie.

Ejemplo 27.2.
Consideremos la serie armónica:
\begin{equation*}
\sum_{n=1}^\infty z_n = \sum_{n=1}^\infty \frac{1}{n}.
\end{equation*}

De nuestros cursos de Cálculo sabemos que $\lim\limits_{n\to\infty} z_n = 0$. Sin embargo la serie armónica es divergente.

Para verificar esto supongamos que $\sum_{n=0}^\infty \dfrac{1}{n} = L \in \mathbb{R}$.

Notemos que:
\begin{align*}
L & = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + \cdots\\
& > \frac{1}{2} + \frac{1}{2} + \frac{1}{4} + \frac{1}{4} + \frac{1}{6} + \frac{1}{6} + \cdots\\
& = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + \cdots\\
& = L,
\end{align*} es decir $L>L$, lo cual claramente no es posible, por lo que la serie diverge.

Para $m\geq 1$ la expresión $\sum_{n=m+1}^\infty z_n$ es llamada una cola de la serie $\sum_{n=0}^\infty z_n$. Para un $m$ fijo la cola de una serie es en sí misma una serie, la cual difiere en una cantidad finita de la serie original.

Corolario 27.2.
Una serie de números complejos $\sum_{n=0}^\infty z_n$ converge si y solo si su cola $\sum_{n=M}^\infty$ converge, donde $M$ es un número natural fijo.

Demostración. Dadas las hipótesis, consideremos a $s_n = \sum_{k=0}^n z_k$ como la $n$-ésima suma parcial de la serie $\sum_{n=0}^\infty z_n$. Definimos:
\begin{equation*}
s_n^M = \sum_{k=M}^n z_k,
\end{equation*} como la $n$-ésima suma parcial de la cola $\sum_{n=M}^\infty z_n$.

Notemos que si $n,m\geq M$, con $n>m$, entonces:
\begin{equation*}
s_n^M – s_m^M = \sum_{k=m+1}^n z_n = s_n – s_m.
\end{equation*}

De acuerdo con lo anterior, es claro que el resultado se sigue del criterio de convergencia de Cauchy tomando $M > N$ en la proposición 27.1.

$\blacksquare$

Observación 27.4.
En este punto es importante recordar la convención que establecimos en la observación 4.7, sobre que $z^0 = 1$ para todo $z\in\mathbb{C}$.

Ejemplo 27.3.
Veamos que la serie geométrica $\sum_{n=0}^\infty z^n$ es convergente si $|z|<1$ y en tal caso:
\begin{equation*}
\sum_{n=0}^\infty z^n = \frac{1}{1-z}.
\end{equation*} Mientras que la serie diverge si $|z|\geq 1$.

Solución. Consideremos a la $(n+1)$-ésima suma parcial, es decir:
\begin{equation*}
s_n = 1 + z + z^2 + \cdots + z^n.
\end{equation*}

Multiplicando por $z$ y sumando 1 en la igualdad anterior tenemos:
\begin{equation*}
1 + z s_n = 1 + z + z^2 + z^3 + \cdots + z^{n+1} = s_n + z^{n+1},
\end{equation*} de donde $s_n(z-1) = z^{n+1} – 1$.

Para $z\neq 1$, tenemos que:
\begin{equation*}
s_n = \frac{z^{n+1} – 1}{z-1} = \frac{1 – z^{n+1}}{1-z} = \frac{(1 + z + z^2 + \cdots + z^n)(1-z)}{(1-z)}.
\end{equation*}

De acuerdo con el ejercicio 4 de la entrada 8, sabemos que la sucesión $\left\{z^n\right\}_{n\geq 0}$ converge a $0$ si $|z|<1$ y diverge si $|z|> 1$.

Entonces, para $|z|<1$ tenemos que:
\begin{equation*}
\lim_{n\to\infty} s_n = \lim_{n\to\infty} (1 + z + z^2 + z^3 + \cdots + z^{n}) = \lim_{n\to\infty} \frac{1 – z^{n+1}}{1-z} = \frac{1}{1-z},
\end{equation*}

de donde:
\begin{equation*}
\sum_{n=0}^\infty z^n = \frac{1}{1-z}, \quad \text{si} \,\,\, |z|<1.
\end{equation*}

Es claro que en nuestro desarrollo anterior la condición $z\neq 1$ es necesaria y está dada si $|z|\neq 1$, pero ¿qué pasa si $|z| = 1$?

Si $|z| = 1$, entonces:
\begin{equation*}
\lim_{n\to \infty}\left| z^n \right| = \lim_{n\to \infty} \left|z \right|^n = 1 \neq 0,
\end{equation*} por lo que, de acuerdo con el ejercicio 6 de la entrada 8, $\lim\limits_{n\to \infty} z^n \neq 0$, entonces si $|z|\geq 1$ la serie diverge.

Podemos visualizar la convergencia o divergencia de la serie geométrica en el plano complejo $\mathbb{C}$ mediante el siguiente Applet en GeoGebra: https://www.geogebra.org/m/jj65zt24.

La serie geométrica suele aparecer en muchos problemas prácticos, por lo que conocer su región de convergencia nos es de gran utilidad.

Ejemplo 27.4.
Obtengamos la mayor región de convergencia de la serie $\sum_{n=0}^\infty \left(4+2z\right)^{-n}$. Después determinemos el valor al que converge.

Solución. Primeramente notemos que si $z=-2$, entonces la expresión en el denominador se anula, por lo que dicho punto no puede estar en la región de convergencia de la serie.

Por otra parte, si hacemos $w=\dfrac{1}{4+2z}$, entonces la serie dada tiene la forma de una serie geométrica $\sum_{n=0}^\infty w^n$.

De acuerdo con el ejemplo anterior, sabemos que la serie geométrica $\sum_{n=0}^\infty w^n$ converge a $\dfrac{1}{1-w}$ si $|w|<1$.

Tenemos que:
\begin{equation*}
|w|<1 \quad \Longleftrightarrow \quad \left| \frac{1}{4+2z}\right| <1 \quad \Longleftrightarrow \quad 1 < \left|4+2z\right| \quad \Longleftrightarrow \quad \frac{1}{2} < \left|z-(-2)\right|.
\end{equation*}

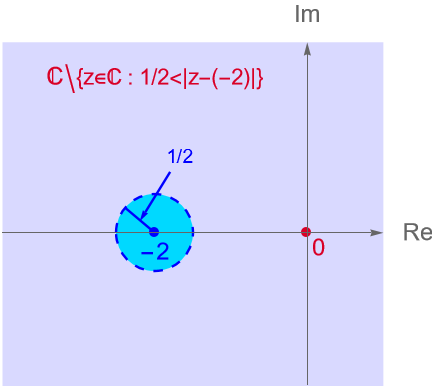
De acuerdo con los resultados de la entrada 6, sabemos que este conjunto corresponde con los puntos en el plano complejo que caen fuera de la circunferencia centrada en el punto $-2$ y de radio $\frac{1}{2}$, es decir, los $z \in \mathbb{C}$ tales que su distancia al punto $-2$ es estrictamente mayor que $\frac{1}{2}$. Bajo esta condición es claro que $z\neq -2$, figura 105.

Entonces, la región de convergencia de la serie está dada por los $z\in\mathbb{C}$ tales que $\frac{1}{2} < \left|z-(-2)\right|$. Para dichos $z$ se tiene que:
\begin{equation*}
\sum_{n=0}^\infty \frac{1}{\left(4+2z\right)^n} = \dfrac{1}{1 – \dfrac{1}{4+2z}} = \dfrac{4+2z}{3+2z}.
\end{equation*}

Proposición 27.2.
Sean $\sum_{n=0}^\infty z_n$, $\sum_{n=0}^\infty w_n$ dos series de números complejos convergentes y $\alpha, \beta \in\mathbb{C}$ constantes. Entonces:

1. $\sum_{n=0}^\infty \left(\alpha z_n \pm \beta w_n\right) = \alpha \sum_{n=0}^\infty z_n \pm \beta \sum_{n=0}^\infty w_n$.
2. La serie $\sum_{n=0}^\infty\,\overline{z_n}$ converge y $\overline{\sum_{n=0}^\infty z_n} = \sum_{n=0}^\infty \,\overline{z_n}$.

Demostración. Dadas las hipótesis.

1. Se deja como ejercicio al lector.
2. Sea $\varepsilon>0$. Como la serie $\sum_{n=0}^\infty z_n$ converge, digamos a $s\in\mathbb{C}$, tenemos que existe $N\in\mathbb{N}$ tal que si $n\geq N$, entonces: \begin{equation*} \left|\sum_{k=0}^n \overline{z_k} – \overline{s}\right| = \left|\overline{\sum_{k=0}^n z_k} – \overline{s}\right| = \left|\overline{\sum_{k=0}^n z_k – s}\right| = \left|\sum_{k=0}^n z_k – s\right| = \left|s_n – s\right| < \varepsilon, \end{equation*} es decir $\overline{\sum_{n=0}^\infty z_n} = \sum_{n=0}^\infty \, \overline{z_n} = \overline{s} \in \mathbb{C}$.

$\blacksquare$

Ejemplo 27.5.
Estudiemos la convergencia de la serie $\sum_{n=3}^\infty \left(\dfrac{i}{2}\right)^n$.

Solución. Tenemos que:
\begin{align*}
\sum_{n=3}^\infty \left(\frac{i}{2}\right)^n = \sum_{n=3}^\infty \left(\frac{i}{2}\right)^3 \left(\frac{i}{2}\right)^{n-3} & = \left(\frac{i}{2}\right)^3 \sum_{n=3}^\infty \left(\frac{i}{2}\right)^{n-3},\quad\quad \text{proposición 27.2,}\\
& = \left(\frac{i}{2}\right)^3 \sum_{k=0}^\infty \left(\frac{i}{2}\right)^{k},\quad \quad \text{cambio de índice} \,\,\, k=n-3,\\
& = \left(\frac{i}{2}\right)^3 \left(\frac{1}{1-\dfrac{i}{2}}\right),\quad \quad \left|\frac{i}{2}\right| = \frac{1}{2} < 1,\\
& =\frac{1}{20} \left(1-2i\right).
\end{align*}

Corolario 27.3.
Sea $z_n = x_n + iy_n \in \mathbb{C}$, con $x_n, y_n \in\mathbb{R}$, para todo $n\in\mathbb{N}$. Entonces, la serie de números complejos $\sum_{n=0}^\infty z_n$ converge a $s=x+iy \in\mathbb{C}$ si y solo si las series de números reales $\sum_{n=0}^\infty x_n$ y $\sum_{n=0}^\infty y_n$ convergen a $x$ y a $y$, respectivamente. En tal caso:
\begin{equation*}
\sum_{n=0}^\infty z_n = \sum_{n=0}^\infty x_n + i \sum_{n=0}^\infty y_n.
\end{equation*}

Demostración. De acuerdo con la proposición 8.3, tenemos que:
\begin{align*}
\sum_{n=0}^\infty z_n = s \quad & \Longleftrightarrow \quad \sum_{n=0}^\infty (x_n+iy_n) = x+iy,\\
\quad & \Longleftrightarrow \quad \lim_{n \to \infty} s_n = \lim_{n \to \infty} \left( \sum_{k=0}^n x_k + i \sum_{k=0}^n y_k\right) = x+iy,\\
\quad & \Longleftrightarrow \quad \lim_{n \to \infty} \sum_{k=0}^n x_k = x \,\,\, \text{y} \,\,\, \lim_{n \to \infty} \sum_{k=0}^n y_k = y,\\
\quad & \Longleftrightarrow \quad \sum_{n=0}^\infty x_n = x \,\,\, \text{y} \,\,\, \sum_{n=0}^\infty y_n = y,\\
\quad & \Longleftrightarrow \quad \sum_{n=0}^\infty x_n +i \sum_{n=0}^\infty y_n = \sum_{n=0}^\infty (x_n + i y_n) = \sum_{n=0}^\infty z_n.
\end{align*}

$\blacksquare$

Observación 27.5.
Del corolario anterior se sigue que para toda serie convergente de números complejos, $\sum_{n=0}^\infty z_n$, se cumple que:
\begin{equation*}
\operatorname{Re}\left( \sum_{n=0}^\infty z_n \right) = \sum_{n=0}^\infty \operatorname{Re}(z_n) \quad \text{e} \quad \operatorname{Im}\left( \sum_{n=0}^\infty z_n \right) = \sum_{n=0}^\infty \operatorname{Im}(z_n).
\end{equation*}

Ejemplo 27.6.
Estudiemos la convergencia de la serie:
\begin{equation*}
\sum_{n=0}^\infty z_n = \sum_{n=0}^\infty \left(\frac{1}{2^n} + \frac{i}{3^n}\right).
\end{equation*}

Solución. Notemos que el $(n+1)$-ésimo término de la serie es $z_n = \dfrac{1}{2^n} + \dfrac{i}{3^n}$, por lo que:
\begin{equation*}
\operatorname{Re}(z_n) = \frac{1}{2^n}, \quad \operatorname{Im}(z_n) = \frac{1}{3^n}.
\end{equation*}

De lo anterior es claro que las dos series reales, correspondientes a las partes real e imaginaria de la serie, son ambas series geométricas convergentes, es decir:
\begin{equation*}
\sum_{n=0}^\infty \operatorname{Re}(z_n) = \sum_{n=0}^\infty \frac{1}{2^n} = \frac{1}{1-\dfrac{1}{2}} = 2,
\end{equation*}
\begin{equation*}
\sum_{n=0}^\infty \operatorname{Im}(z_n) = \sum_{n=0}^\infty \frac{1}{3^n} = \frac{1}{1-\dfrac{1}{3}} = \frac{3}{2}.
\end{equation*}

Por lo tanto, del corolario 27.2 se sigue que la serie $\sum_{n=0}^\infty z_n$ es convergente y su suma es:
\begin{equation*}
\sum_{n=0}^\infty z_n = \sum_{n=0}^\infty \left(\frac{1}{2^n} + \frac{i}{3^n}\right) = \sum_{n=0}^\infty \frac{1}{2^n} + i \sum_{n=0}^\infty \frac{1}{3^n} = 2 + i \frac{3}{2}.
\end{equation*}

Definición 27.3. (Serie absolutamente convergente.)
Una serie de números complejos $\sum_{n=0}^\infty z_n$ es absolutamente convergente si la serie $\sum_{n=0}^\infty |z_n|$ es convergente.

Definición 29.4. (Serie condicionalmente convergente.)
Una serie de números complejos $\sum_{n=0}^\infty z_n$ es condicionalmente convergente si la serie $\sum_{n=0}^\infty z_n$ es convergente, pero no es absolutamente convergente.

Proposición 27.3.
Una serie de números complejos $\sum_{n=0}^\infty z_n$ absolutamente convergente, es convergente y cumple que:
\begin{equation*}
\left|\sum_{n=0}^\infty z_n\right| \leq \sum_{n=0}^\infty |z_n|.
\end{equation*}

Demostración.
Dadas las hipótesis, sea $\left\{s_n\right\}_{n\geq 0}$ la sucesión de sumas parciales de la serie $\sum_{n=0}^\infty z_n$.

Sea $\varepsilon>0$. De acuerdo con el criterio de convergencia de Cauchy, proposición 27.1, tenemos que existe $N\in\mathbb{N}$ tal que si $n,m \geq N$, con $n>m$, entonces:
\begin{equation*}
\sum_{k=m+1}^n |z_k| = \left|\sum_{k=m+1}^n |z_k|\right| < \varepsilon.
\end{equation*}

Por la desigualdad del triángulo, observación 3.6 entrada 3, se cumple que:
\begin{equation*}
|s_n – s_m| = \left|\sum_{k=0}^n z_k – \sum_{k=0}^m z_k\right| = \left|\sum_{k=m+1}^n z_k\right| \leq \sum_{k=m+1}^n |z_k| < \varepsilon,
\end{equation*} es decir que la sucesión de sumas parciales $\left\{s_n\right\}_{n\geq 0}$ es de Cauchy, por lo que, al ser $\mathbb{C}$ un espacio métrico completo, proposición 8.5, se tiene que la sucesión $\left\{s_n\right\}_{n\geq 0}$ es convergente, entonces la serie $\sum_{n=0}^\infty z_n$ converge.

De acuerdo con el ejercicio 3 de la entrada 8, sabemos que si una sucesión $\left\{w_n\right\}_{n\geq 0}$ converge a $w\in\mathbb{C}$, entonces la sucesión $\left\{|w_n|\right\}_{n\geq 0}$ converge a $|w|$.

Como la sucesión $\left\{s_n\right\}_{n\geq 0}$ converge, digamos a $s\in\mathbb{C}$, entonces:
\begin{equation*}
\lim_{n\to\infty} |s_n| = \lim_{n\to\infty} \left|\sum_{k=0}^n z_k\right| = \left|\sum_{n=0}^\infty z_n\right| = |s|.
\end{equation*}

Análogamente, como la serie $\sum_{n=0}^\infty |z_n|$ es convergente, tenemos que:
\begin{equation*}
\lim_{n\to\infty} \left|\sum_{k=0}^n |z_k|\right| = \lim_{n\to\infty} \sum_{k=0}^n |z_k| = \sum_{n=0}^\infty |z_n|.
\end{equation*}

Nuevamente, de la desigualdad del triángulo, observación 3.6, se sigue que:
\begin{equation*}
\left|\sum_{k=0}^n z_k\right| \leq \sum_{k=0}^n |z_k|.
\end{equation*}

Considerando lo anterior y el ejercicio 8 de la entrada 8, concluimos que:
\begin{equation*}
\left|\sum_{n=0}^\infty z_n\right| \leq \sum_{n=0}^\infty |z_n|.
\end{equation*}

$\blacksquare$

Corolario 27.4.
Sea $z_n = x_n + iy_n \in \mathbb{C}$, con $x_n, y_n \in\mathbb{R}$, para todo $n\in\mathbb{N}$. Entonces, la serie de números complejos $\sum_{n=0}^\infty z_n$ converge absolutamente a $s=x+iy \in\mathbb{C}$ si y solo si las series de números reales $\sum_{n=0}^\infty x_n$ y $\sum_{n=0}^\infty y_n$ convergen absolutamente a $x$ y a $y$, respectivamente. En tal caso:
\begin{equation*}
\sum_{n=0}^\infty z_n = \sum_{n=0}^\infty x_n + i \sum_{n=0}^\infty y_n.
\end{equation*}

Demostración. Se deja como ejercicio al lector.

$\blacksquare$

Proposición 27.4. (Criterio de comparación de Weierstrass.)
Sea $\left\{a_n\right\}_{n\geq 0}$ una sucesión de números reales no negativos y sea $\left\{z_n\right\}_{n\geq 0}$ una sucesión de números complejos. Supongamos que $|z_n| \leq a_n$ para todo $n\geq j$, para algún $j\in\mathbb{N}$.

1. Si la serie $\sum_{n=0}^\infty a_n$ converge, entonces la serie $\sum_{n=0}^\infty z_n$ es absolutamente convergente.
2. Si la serie $\sum_{n=0}^\infty z_n$ diverge, entonces la serie $\sum_{n=0}^\infty a_n$ es divergente.

Demostración. Dadas las hipótesis, sea $\left\{s_n\right\}_{n\geq 0}$ la sucesión de sumas parciales de la serie $\sum_{n=0}^\infty |z_n|$.

1. Sea $\varepsilon>0$. Por el criterio de Cauchy, proposición 27.1, tenemos que existe $N\in\mathbb{N}$ tal que si $n>m\geq N > j$, entonces:
   \begin{equation*}
   \left|s_n – s_m \right| = \left|\sum_{k=m+1}^n |z_k|\right| = \sum_{k=m+1}^n |z_k| \leq \sum_{k=m+1}^n a_k = \left|\sum_{k=m+1}^n a_k \right| <\varepsilon, \end{equation*} es decir, la sucesión $\left\{s_n\right\}_{n\geq 0}$ es de Cauchy, por lo que, al ser $\mathbb{C}$ un espacio métrico completo, la sucesión de sumas parciales converge, entonces la serie $\sum_{n=0}^\infty |z_n|$ converge y por tanto la serie $\sum_{n=0}^\infty z_n$ es absolutamente convergente.
2. Es la contrapuesta del caso anterior.

$\blacksquare$

Ejemplo 27.7.
Veamos que las siguientes series son convergentes.
a) $\displaystyle \sum_{n=0}^\infty \dfrac{3+2i}{\left(n+1\right)^n}$.
b) $\displaystyle \sum_{n=0}^\infty \dfrac{2\operatorname{cos}(n\theta) + i 2\operatorname{sen}(n\theta)}{n^2+3}$.

Solución.

a) Procedemos a probar la convergencia de la serie utilizando el criterio de comparación. Para ello consideremos a la serie geométrica:
\begin{equation*}
\sum_{n=0}^\infty \frac{1}{2^n},
\end{equation*} la cual es convergente.

Notemos que:
\begin{equation*}
|3+2i| = \sqrt{3^2+2^2} = \sqrt{13} < 4,
\end{equation*}

por lo que:
\begin{equation*}
\left|\frac{3+2i}{\left(n+1\right)^n}\right| = \frac{|3+2i|}{\left(n+1\right)^n} = \frac{\sqrt{13}}{\left(n+1\right)^n} < \frac{4}{\left(n+1\right)^n}.
\end{equation*}

Por otra parte, es sencillo verificar que para $n\geq 3$ se cumple que:
\begin{equation*}
\left|\frac{3+2i}{\left(n+1\right)^n}\right| < \frac{4}{\left(n+1\right)^n} < \frac{1}{2^n},
\end{equation*}

por lo que se deja como ejercicio al lector.

Entonces, por el criterio de comparación, concluimos que la serie dada es absolutamente convergente y por tanto converge.

b) De nueva cuenta, procedemos a probar la convergencia de la serie utilizando el criterio de comparación. Consideremos a la serie convergente:
\begin{equation*}
\sum_{n=1}^\infty \frac{2}{n^2}.
\end{equation*}

Notemos que:
\begin{equation*}
\left|\dfrac{2\operatorname{cos}(n\theta) + i 2\operatorname{sen}(n\theta)}{n^2+3}\right| \leq \dfrac{2 \left| \operatorname{cos}(n\theta) + i \operatorname{sen}(n\theta)\right|}{n^2} = \dfrac{2}{n^2}.
\end{equation*}

Entonces, por el criterio de comparación, concluimos que la serie:
\begin{equation*}
\sum_{n=1}^\infty \dfrac{2\operatorname{cos}(n\theta) + i 2\operatorname{sen}(n\theta)}{n^2+3},
\end{equation*}

es convergente, por lo que, de acuerdo con el corolario 27.2, la serie original converge.

Proposición 27.5. (Criterio de la razón o del cociente de D’Alembert.)
Sea $\left\{ z_n\right\}_{n\geq 0}$ una sucesión de números complejos distintos de cero, tales que:
\begin{equation*}
\lim_{n\to \infty} \frac{|z_{n+1}|}{|z_{n}|} = \lambda,
\end{equation*} existe o es infinito.

1. Si $\lambda <1$, entonces la serie $\sum_{n=0}^\infty z_n$ es absolutamente convergente.
2. Si $\lambda >1$ ó $\lambda=\infty$, entonces la serie $\sum_{n=0}^\infty z_n$ es divergente.
3. Si $\lambda =1$, entonces la serie $\sum_{n=0}^\infty z_n$ puede diverger o converger.

Demostración. Dadas las hipótesis, como $z_n \neq 0$ para todo $n\in\mathbb{N}$, entonces:
\begin{equation*}
\left| \frac{z_{n+1}}{z_{n}} \right| = \frac{|z_{n+1}|}{|z_{n}|} > 0, \quad \forall n\in\mathbb{N}.
\end{equation*}

De lo anterior es claro que si $\lim_{n\to \infty} \dfrac{|z_{n+1}|}{|z_{n}|} = \lambda \in \mathbb{R}$, entonces $\lambda\geq 0$.

1. Supongamos que $\lambda \in \mathbb{R}$ con $0 \leq \lambda <1$. Sea $r = \dfrac{\lambda+1}{2}$, entonces $0\leq \lambda < r < 1$.
   Para $\varepsilon = r – \lambda>0$, tenemos que existe $N\in\mathbb{N}$ tal que si $n\geq N$, entonces: \begin{equation*} \left| \left| \frac{z_{n+1}}{z_{n}} \right| – \lambda \right| < \varepsilon \quad \Longrightarrow \quad \frac{|z_{n+1}|}{|z_{n}|} < \varepsilon + \lambda = r, \end{equation*} de donde se sigue que: \begin{equation*} |z_{n+1}| < r |z_{n}| \quad \forall n\geq N. \end{equation*} Considerando lo anterior, para $ n\geq N$ tenemos que: \begin{align*}
   |z_{N+1}| & < r |z_{N}|\\
   |z_{N+2}| & < r |z_{N+1}| < r^2 |z_{N}|\\
   |z_{N+3}| & < r |z_{N+2}| < r^3 |z_{N}|\\
   & \,\,\,\,\vdots\\
   |z_{n}| & < r^{n-N} |z_{N}|\\
   & \,\,\,\,\vdots
   \end{align*} Dado que $r<1$, notemos que: \begin{equation*} \sum_{n = N}^{\infty} r^{n-N} = \sum_{k = 0}^{\infty} r^{k},\end{equation*} es una serie geométrica convergente. Por lo que, de acuerdo con la proposición 27.2, tenemos que la serie $\sum_{n=N}^\infty r^{n-N} |z_{N}|$ converge, entonces por el criterio de comparación se sigue que la serie $\sum_{n=N}^\infty |z_{n}|$ converge y por el corolario 27.2 concluimos que la serie $\sum_{n=0}^\infty |z_{n}|$ converge.
   
   Entonces, la serie $\sum_{n=0}^\infty z_{n}$ es absolutamente convergente y por tanto converge, proposición 27.3.
2. Supongamos que $\lambda>1$. Sea $r=\dfrac{\lambda +1}{2}$, el cual cumple que $1<r<\lambda$. Procediendo como en el caso anterior, para $\varepsilon = \lambda – r > 0$ existe $N\in\mathbb{N}$ tal que si $n\geq N$ entonces: \begin{equation*} |z_{n+1}| > r |z_{n}|, \end{equation*} de donde se sigue que: \begin{equation*} |z_{n}| > r^{n-N} |z_{N}| > 0, \quad \forall n\geq N, \end{equation*} por lo que $\lim\limits_{n\to\infty} |z_{n}| \neq 0$, entonces $\lim\limits_{n\to\infty} z_{n} \neq 0$ y por tanto la serie $\sum_{n=0}^\infty z_n$ es divergente, corolario 27.1.
   
   Análogamente, si $\lambda=\infty$, tenemos que para todo $M >0$ existe un $N\in\mathbb{N}$ tal que si $n\geq N$ entonces: \begin{equation*} |z_{n}| > M^{n-N} |z_{N}| > 0, \end{equation*} de donde se sigue que la serie $\sum_{n=0}^\infty z_n$ diverge.
3. Consideremos a las series: \begin{equation*} \sum_{n=1}^\infty \frac{1}{n} \quad \text{y} \quad \sum_{n=1}^\infty \frac{1}{n^2}. \end{equation*} Para ambas se cumple que $z_n \neq 0$ para todo $n\in\mathbb{N}^+$ y que: \begin{equation*} \lim_{n\to \infty} \frac{\dfrac{1}{n+1}}{\dfrac{1}{n}} = \lim_{n\to \infty} \frac{n}{n+1} = 1 = \lambda.\end{equation*} \begin{equation*} \lim_{n\to \infty} \frac{\dfrac{1}{(n+1)^2}}{ \dfrac{1}{n^2}} = \lim_{n\to \infty} \frac{n^2}{(n+1)^2} = 1 = \lambda.\end{equation*} Sin embargo, de acuerdo con el ejemplo 27.2, sabemos que la primera serie diverge, mientras que, utilizando el criterio de comparación y la serie $ \displaystyle\sum_{n=2}^\infty \dfrac{1}{n^2 – n}$, se puede verificar que la segunda serie converge. Entonces, si $\lambda = 1$ el criterio no es concluyente.

$\blacksquare$

Ejemplo 27.8.
Sea $z\in\mathbb{C}$. Estudiemos la convergencia de la serie $\sum_{n=0}^\infty \dfrac{z^n}{n!}$.

Solución. Sea $z_n = \dfrac{z^n}{n!}$, entonces $|z_n| = \dfrac{|z|^n}{n!} \geq 0$. Si $z=0$, es claro que la serie converge.

Supongamos que $z\neq 0$, entonces $z_n\neq 0$ para todo $n\in\mathbb{N}$. Tenemos que:
\begin{equation*}
\lim_{n\to\infty} \frac{\left|z_{n+1}\right|}{\left|z_{n}\right|} = \lim_{n\to\infty} \frac{\dfrac{\left|z\right|^{n+1}}{(n+1)!}}{\dfrac{\left|z\right|^{n}}{n!}} = \lim_{n\to\infty} \frac{\left|z\right|}{n+1} = 0 < 1,
\end{equation*}

por lo que la serie $\sum_{n=0}^\infty \dfrac{z^n}{n!}$ es absolutamente convergente para todo $z\in\mathbb{C}$.

Ejemplo 27.9.
Analicemos el comportamiento de las siguientes series.
a) $\displaystyle \sum_{n=0}^\infty \dfrac{(1-i)^n}{n!}$.
b) $\displaystyle \sum_{n=0}^\infty \dfrac{(z-i)^n}{2^n}$.

Solución.

a) Sea $z_n = \dfrac{(1-i)^n}{n!}$ el $(n+1)$-ésimo término de la serie. Claramente $z_n \neq 0$ para toda $n\in\mathbb{N}$.

Considerando el criterio de la razón, proposición 27.5, tenemos que:
\begin{align*}
\lambda = \lim_{n\to\infty} \frac{\left|z_{n+1}\right|}{\left|z_{n}\right|} = \lim_{n\to\infty} \left|\frac{\dfrac{(1-i)^{n+1}}{(n+1)!}}{\dfrac{(1-i)^{n}}{n!}}\right| & = \lim_{n\to\infty} \left|\frac{(1-i)^{n+1} n!}{(1-i)^{n}(n+1) n!}\right|\\
& = \lim_{n\to\infty} \frac{\left|1-i\right|}{n+1}\\
& = \lim_{n\to\infty} \frac{\sqrt{2}}{n+1}\\
& = 0.
\end{align*} Como $\lambda < 1$, entonces la serie converge.

b) Sea $z_n = \dfrac{(z-i)^n}{2^n}$ el $(n+1)$-ésimo término de la serie. Notemos que si $z=i$, entonces la serie converge.

Supongamos que $z \neq i$, entonces para todo $n\in\mathbb{N}$ se cumple que $z_n \neq 0$. Tenemos que:
\begin{align*}
\lambda = \lim_{n\to\infty} \frac{\left|z_{n+1}\right|}{\left|z_{n}\right|} = \lim_{n\to\infty} \left|\frac{\dfrac{(z-i)^{n+1}}{2^{n+1}}}{\dfrac{(z-i)^{n}}{2^{n}}}\right| & = \lim_{n\to\infty} \left|\frac{2^n (z-i)^{n+1}}{2^{n+1}(z-i)^{n}}\right|\\
& = \lim_{n\to\infty} \frac{\left|z-i\right|}{2}\\
& = \frac{\left|z-i\right|}{2}.
\end{align*}

Por el criterio de la razón, proposición 27.5, tenemos que $\lambda < 1$ si $\left|z-i\right| < 2$, en tal caso la serie converge.

Por otra parte, $\lambda > 1$ si $\left|z-i\right| > 2$, en tal caso la serie diverge.

Por último, tenemos que:
\begin{equation*}
\left|z-i\right| < 2 \quad \Longrightarrow \quad \left|\frac{z-i}{2}\right| < 1,
\end{equation*}

es decir, la serie dada es una serie geométrica convergente si $\left|z-i\right| < 2$, en tal caso:
\begin{equation*}
\sum_{n=0}^\infty \dfrac{(z-i)^n}{2^n} = \sum_{n=0}^\infty\left(\dfrac{z-i}{2}\right)^n = \frac{1}{1 – \dfrac{z-i}{2}} = \frac{2}{2-(z – i)}.
\end{equation*}

Y para $\left|z-i\right| \geq 2$ la serie diverge.

Proposición 27.6. (Criterio de la raíz.)
Sea $\left\{ z_n\right\}_{n\geq 0}$ una sucesión de números complejos, tales que:
\begin{equation*}
\lim_{n\to \infty} = |z_n|^{1/n} = \lambda,
\end{equation*} existe o es infinito.

1. Si $\lambda <1$, entonces la serie $\sum_{n=0}^\infty z_n$ es absolutamente convergente.
2. Si $\lambda >1$ ó $\lambda=\infty$, entonces la serie $\sum_{n=0}^\infty z_n$ es divergente.
3. Si $\lambda =1$, entonces la serie $\sum_{n=0}^\infty z_n$ puede diverger o converger.

Demostración. La prueba es análoga a la de la proposición 27.5, por lo que los detalles se dejan como ejercicio al lector.

Dadas las hipótesis.

1. Supongamos que $\lambda \in \mathbb{R}$ con $0 \leq \lambda <1$. Elegimos a $r\in\mathbb{R}$ tal que $\lambda < r < 1$. Tenemos que existe $N\in\mathbb{N}$ tal que si $n\geq N$, entonces: \begin{equation*} \left|z_n\right|^{1/n} < r \quad \Longrightarrow \quad \left|z_n\right| < r^n. \end{equation*} Dado que $r<1$, tenemos que la serie geométrica $\sum_{n = N}^{\infty} r^{n}$ converge, entonces por el criterio de comparación se sigue que la serie $\sum_{n=N}^\infty |z_{n}|$ converge y por el corolario 27.2 concluimos que la serie $\sum_{n=0}^\infty |z_{n}|$ converge.
   
   Entonces, la serie $\sum_{n=0}^\infty z_{n}$ es absolutamente convergente y por tanto converge.
2. Si $\lambda>1$ ó $\lambda=\infty$. Tomemos a $r\in\mathbb{R}$ tal que $1<r<\lambda$. Tenemos que existe $N\in\mathbb{N}$ tal que si $n\geq N$, entonces: \begin{equation*} \left|z_n\right|^{1/n} > r \quad \Longrightarrow \quad \left|z_n\right| > r^n > 1.\end{equation*} Por lo que $\lim\limits_{n\to\infty} z_{n} \neq 0$ y por tanto la serie $\sum_{n=0}^\infty z_n$ es divergente.
3. Consideremos a las series: \begin{equation*} \sum_{n=1}^\infty \frac{1}{n} \quad \text{y} \quad \sum_{n=1}^\infty \frac{1}{n^2}. \end{equation*} Para ambas se cumple que: \begin{equation*} \lim_{n\to \infty} \left|\frac{1}{n}\right|^{1/n} = \lim_{n\to \infty} \left(\frac{1}{n}\right)^{1/n} 1 = \lambda. \end{equation*} \begin{equation*} \lim_{n\to \infty} \left|\frac{1}{n^2}\right|^{1/n} = \lim_{n\to \infty} \left(\frac{1}{n^2}\right)^{1/n} 1 = \lambda. \end{equation*} Sin embargo, la primera serie diverge, mientras que la segunda serie converge. Entonces, si $\lambda = 1$ el criterio no es concluyente.

En general, el criterio de la razón es más fácil de aplicar que el criterio de la raíz, aunque existen ciertos casos donde la forma de la sucesión hace evidente el uso del criterio de la raíz.

Ejemplo 27.10.
Analicemos el comportamiento de las siguientes series.
a) $\displaystyle \sum_{n=0}^\infty \dfrac{z^n}{(n+1)^n}$.
b) $\displaystyle \sum_{n=0}^\infty \dfrac{(1+i)^n}{3^n}$.

Solución.

a)] Sea $z_n = \left(\dfrac{z}{n+1}\right)^n$ el $(n+1)$-ésimo término de la sucesión, entonces:
\begin{equation*}
\lambda = \lim_{n\to\infty}\left|z_{n}\right|^{1/n} = \lim_{n\to\infty}\left|\left(\dfrac{z}{n+1}\right)^n\right|^{1/n} = \lim_{n\to\infty} \dfrac{\left|z\right|}{n+1} = 0.
\end{equation*}

Como $\lambda < 1$, entonces por el criterio de la raíz tenemos que la serie converge.

b) Sea $z_n = \left(\dfrac{1+i}{3}\right)^n$ el $(n+1)$-ésimo término de la sucesión, entonces:
\begin{equation*}
\lambda = \lim_{n\to\infty}\left|z_{n}\right|^{1/n} = \lim_{n\to\infty}\left|\left(\dfrac{1+i}{3}\right)^n\right|^{1/n} = \lim_{n\to\infty} \dfrac{\left|1+i\right|}{3} = \frac{\sqrt{2}}{3}.
\end{equation*}

Como $\lambda < 1$, entonces por el criterio de la raíz tenemos que la serie converge.

Dado que $\left|\dfrac{1+i}{3}\right|<1$, entonces la serie es geométrica, por lo que:
\begin{equation*}
\sum_{n=0}^\infty \dfrac{(1+i)^n}{3^n} = \frac{1}{1-\dfrac{1+i}{3}} = \frac{3}{2-i}.
\end{equation*}

Definición 27.5. (Producto de Cauchy para series.)
Sean $\sum_{n=0}^\infty z_n$ y $\sum_{n=0}^\infty w_n$ dos series de números complejos. Definimos el producto de ambas series como la serie $\sum_{n=0}^\infty c_n$ cuyo $n$-ésimo término está dado como:
\begin{equation*}
c_n = z_0 w_n + z_1 w_{n-1} + \cdots + z_{n-1} w_1 + z_n w_0 = \sum_{k=0}^n z_k w_{n-k}. \tag{27.1}
\end{equation*}

La serie:
\begin{equation*}
\sum_{n=0}^\infty c_n = \sum_{n=0}^\infty \left(\sum_{k=0}^n z_k w_{n-k}\right). \tag{27.2}
\end{equation*} es llamada el producto de Cauchy de las series $\sum_{n=0}^\infty z_n$ y $\sum_{n=0}^\infty w_n$.

Ejemplo 27.11.
Sean $z,w \in\mathbb{C}$. Obtengamos el producto de Cauchy de las series:
\begin{equation*}
\sum_{n=0}^\infty \frac{z^n}{n!} \quad \text{y} \quad \sum_{n=0}^\infty \frac{w^n}{n!}.
\end{equation*}

Solución. Sean $z_n = \dfrac{z^n}{n!}$ y $w_n = \dfrac{w^n}{n!}$ para todo $n\in\mathbb{N}$. De acuerdo con (29.2) tenemos que:
\begin{align*}
\sum_{n=0}^\infty c_n = \sum_{n=0}^\infty \left(\sum_{k=0}^n z_k w_{n-k}\right) & = \sum_{n=0}^\infty \left( \sum_{k=0}^n \frac{z^k}{k!} \frac{w^{n-k}}{(n-k)!} \right)\\
& = \sum_{n=0}^\infty \frac{1}{n!}\left(\sum_{k=0}^n \frac{n!}{k!(n-k)!} z^k w^{n-k} \right)\\
& = \sum_{n=0}^\infty \frac{1}{n!}\left(\sum_{k=0}^n \binom{n}{k} z^k w^{n-k} \right)\\
& = \sum_{n=0}^\infty \frac{(z+w)^n}{n!}.
\end{align*}

Como hemos visto hasta ahora, las series absolutamente convergentes heredan propiedades de convergencia que resultan de gran utilidad en la práctica. Por lo que, en este punto resulta natural preguntarnos sobre cómo se comporta el producto de series de números complejos absolutamente convergentes. Para responder esta pregunta daremos dos resultados que consideran series convergentes y absolutamente convergentes.

Antes de continuar, recordemos el siguiente resultado de nuestros cursos de Cálculo.

Teorema 27.1. (Teorema de la convergencia monótona para sucesiones.)
Sea $\left\{a_n\right\}_{n\geq 0} \subset \mathbb{R}$ una sucesión real monótona. Entonces, $\left\{a_n\right\}_{n\geq 0}$ converge si y solo si es acotada.

Procedemos con los resultados mencionados previamente.

Proposición 27.7. (Producto de Cauchy absolutamente convergente.)
Sean $\sum_{n=0}^\infty z_n$ y $\sum_{n=0}^\infty w_n$ dos series de números complejos absolutamente convergentes. Entonces, el producto de Cauchy de ambas series, es decir la serie $\sum_{n=0}^\infty c_n$ dada en (27.2), es absolutamente convergente y se cumple que:
\begin{equation*}
\sum_{n=0}^\infty c_n = \left(\sum_{n=0}^\infty z_n\right)\left(\sum_{n=0}^\infty w_n\right).
\end{equation*}

Demostración. Dadas las hipótesis, primeramente procedemos a probar que la serie $\sum_{n=0}^\infty c_n$, dada en (27.2), es absolutamente convergente.

Sean:
\begin{equation*}
A = \sum_{n=0}^\infty |z_n|, \quad B = \sum_{n=0}^\infty |w_n|,
\end{equation*}

y sea $s_n = \sum_{j=0}^n |c_j|$ la $n$-ésima suma parcial de la serie $\sum_{n=0}^\infty |c_n|$.

De acuerdo con (27.1), para todo $j\in\mathbb{N}$ tenemos que:
\begin{equation*}
c_j = \sum_{k=0}^j z_k w_{j-k} = z_0 w_j + z_1 w_{j-1} + \cdots + z_{j-1} w_1 + z_j w_0.
\end{equation*}

Notemos que para todo $n\in\mathbb{N}$ se cumple que:
\begin{align*}
\sum_{j=0}^n c_j & = \sum_{j=0}^n \left(\sum_{k=0}^j z_k w_{j-k}\right)\\
& = \sum_{k=0}^0 z_k w_{0-k} + \sum_{k=0}^1 z_k w_{1-k} + \cdots + \sum_{k=0}^n z_k w_{n-k}\\
& = z_0 w_0 + (z_0 w_1 + z_1 w_0) + \cdots + (z_0 w_n + \cdots + z_n w_0)\\
& = \sum_{k=0}^n z_0 w_k + \sum_{k=0}^{n-1} z_1 w_k + \cdots + \sum_{k=0}^1 z_{n-1} w_k + \sum_{k=0}^{0} z_n w_k\\
& = \sum_{j=0}^n \left(\sum_{k=0}^{n-j} z_j w_{k}\right).
\end{align*}

Es claro que se puede verificar esta igualdad por inducción, por lo que se deja como ejercicio al lector.

Por otra parte, para todo $n\in\mathbb{N}$ tenemos que:
\begin{equation*}
s_{n+1} – s_n = \sum_{j=0}^{n+1} |c_j| – \sum_{j=0}^n |c_j| = |c_{n+1}| \geq 0,
\end{equation*}

de donde se sigue que la sucesión de sumas parciales $\left\{s_n\right\}_{n\geq 0}$, de la serie $ \sum_{n=0}^\infty |c_n|$, es creciente, es decir, es una sucesión monótona.

Considerando lo anterior, para todo $n\in\mathbb{N}$ tenemos que:
\begin{align*}
s_n = \sum_{j=0}^n |c_j| = \sum_{j=0}^n \left| \sum_{k=0}^{n-j} z_j w_{k} \right| \leq \sum_{j=0}^n \sum_{k=0}^{n-j} |z_j| |w_{k}| \leq \left(\sum_{j=0}^n |z_j|\right) \left( \sum_{k=0}^{n} |w_{k}|\right) \leq AB.
\end{align*}

Entonces, la sucesión de sumas parciales $\left\{s_n\right\}_{n\geq 0}$, de la serie $ \sum_{n=0}^\infty |c_n|$, es acotada. Por lo que, de acuerdo con el teorema 27.1, la sucesión converge y por tanto la serie $\sum_{n=0}^\infty c_n$ es absolutamente convergente.

Veamos ahora que la serie $\sum_{n=0}^\infty c_n$ converge al producto de las series $\sum_{n=0}^\infty z_n$ y $\sum_{n=0}^\infty w_n$.

De acuerdo con la proposición 27.3, tenemos que:
\begin{align*}
\left| \sum_{j=0}^n c_j – \sum_{j=0}^n z_j \sum_{k=0}^n w_k \right| & \leq \left| \sum_{j=0}^n z_j \sum_{k=0}^{n-j} w_{k} – \sum_{j=0}^n z_j \sum_{k=0}^\infty w_k\right| + \left| \sum_{j=0}^n z_j \sum_{k=0}^\infty w_k – \sum_{j=0}^n z_j \sum_{k=0}^n w_k\right|\\
& = \left| \sum_{j=0}^n z_j \left( \sum_{k=0}^\infty w_k – \sum_{k=0}^{n-j} w_{k}\right)\right| + \left| \sum_{j=0}^n z_j \left( \sum_{k=0}^\infty w_k – \sum_{k=0}^n w_k\right)\right|\\
& = \left| \sum_{j=0}^n z_j \sum_{k=n-j+1}^\infty w_k\right| + \left| \sum_{j=0}^n z_j \sum_{k=n+1}^\infty w_k\right|\\
& \leq \sum_{j=0}^n |z_j| \sum_{k=n-j+1}^\infty |w_k| + \sum_{j=0}^n |z_j| \sum_{k=n+1}^\infty |w_k|.
\end{align*}

Como las series $\sum_{n=0}^\infty z_n$ y $\sum_{n=0}^\infty w_n$ son absolutamente convergentes, de acuerdo con el ejercicio 3 de esta entrada, al tomar límites tenemos que:
\begin{equation*}
\lim_{n \to \infty} \left| \sum_{j=0}^n c_j – \sum_{j=0}^n z_j \sum_{k=0}^n w_k \right| = 0,
\end{equation*}

entonces:
\begin{equation*}
\lim_{n \to \infty} \left(\sum_{j=0}^n c_j – \sum_{j=0}^n z_j \sum_{k=0}^n w_k \right) = 0,
\end{equation*}

de donde se sigue que:
\begin{equation*}
\sum_{n=0}^\infty c_n = \left(\sum_{n=0}^\infty z_n\right)\left(\sum_{n=0}^\infty w_n\right).
\end{equation*}

$\blacksquare$

Ejemplo 27.12.
En el ejemplo 27.11 vimos que la serie:
\begin{equation*}
\sum_{n=0}^\infty c_n = \sum_{n=0}^\infty \frac{(z+w)^n}{n!},
\end{equation*}

es el producto de Cauchy de las series:
\begin{equation*}
\sum_{n=0}^\infty \frac{z^n}{n!} \quad \text{y} \quad \sum_{n=0}^\infty \frac{w^n}{n!}.
\end{equation*}

Mientras que en el ejemplo 27.8 probamos que ambas series son absolutamente convergentes para todo $z, w\in\mathbb{C}$. Por lo que, de acuerdo con la proposición 27.7, concluimos que el producto de Cauchy de estas series es absolutamente convergente y es igual al producto de dichas series, es decir:
\begin{equation*}
\left( \sum_{n=0}^\infty \frac{z^n}{n!} \right) \left( \sum_{n=0}^\infty \frac{w^n}{n!} \right) = \sum_{n=0}^\infty \frac{(z+w)^n}{n!}.
\end{equation*}

Ejemplo 27.13.
Prueba que para $|z|<1$ se tiene que:
\begin{equation*}
\sum_{n=0}^\infty (n+1) z^{n} = \frac{1}{(1-z)^2}.
\end{equation*}

Solución.
Sabemos que la serie geométrica es convergente y se cumple que:
\begin{equation*}
\sum_{n=0}^\infty z^n = \frac{1}{1-z}, \quad \text{si} \,\, |z|<1.
\end{equation*}

Más aún, mediante el criterio de D’Alembert es fácil verificar que dicha serie es absolutamente convergente si $|z|<1$.

Entonces, por la proposición 27.7, tenemos que el producto de Cauchy de la serie geométrica consigo misma es absolutamente convergente y para $|z|<1$ se cumple que:
\begin{align*}
\displaystyle\sum_{n=0}^\infty c_n & = \left(\displaystyle\sum_{n=0}^\infty z^n \right)\left(\displaystyle\sum_{n=0}^\infty z^n\right)\\
& = \left(\frac{1}{1-z}\right)\left(\frac{1}{1-z}\right)\\
& = \frac{1}{(1-z)^2}.
\end{align*}

Procedemos a obtener el producto de Cauchy. Sean $z_n = z^n = w_n$ para todo $n\in\mathbb{N}$, entonces:
\begin{align*}
\sum_{n=0}^\infty c_n = \sum_{n=0}^\infty \left(\sum_{k=0}^n z_k w_{n-k}\right)
& = \sum_{n=0}^\infty \left(\sum_{k=0}^n z^k z^{n-k}\right)\\
& = \sum_{n=0}^\infty z^n \left(\sum_{k=0}^n 1\right)\\
& = \sum_{n=0}^\infty \left(n+1\right) z^n.
\end{align*}

Por lo tanto:
\begin{equation*}
\sum_{n=0}^\infty (n+1) z^{n} = \frac{1}{(1-z)^2}, \quad \text{si} \,\, |z|<1.
\end{equation*}

Proposición 27.8. (Teorema de Mertens sobre la convergencia del producto de Cauchy.)
Sean $\sum_{n=0}^\infty z_n$ y $\sum_{n=0}^\infty w_n$ dos series de números complejos tales que una es absolutamente convergente y la otra es convergente. Entonces, el producto de Cauchy de ambas series, dado en (27.2), es convergente y se cumple que:
\begin{equation*}
\sum_{n=0}^\infty c_n = \left(\sum_{n=0}^\infty z_n\right)\left(\sum_{n=0}^\infty w_n\right).
\end{equation*}

Demostración. Dadas las hipótesis, sin pérdida de generalidad supongamos que $\sum_{n=0}^\infty z_n$ converge a $A\in\mathbb{C}$, $\sum_{n=0}^\infty |z_n| = K \in\mathbb{R}$ y que $\sum_{n=0}^\infty w_n$ converge a $B\in\mathbb{C}$.

Para todo $n\in\mathbb{N}$ definimos las sumas parciales de las series como:
\begin{equation*}
s_n = \sum_{k=0}^n |z_k|, \quad a_n = \sum_{k=0}^n z_k, \quad b_n = \sum_{k=0}^n w_k, \quad C_n = \sum_{k=0}^n c_k.
\end{equation*}

De acuerdo con (27.1), para todo $n\in\mathbb{N}$ se cumple que:
\begin{equation*}
C_n = \sum_{j=0}^n c_j = \sum_{j=0}^n \left(\sum_{k=0}^j z_k w_{j-k}\right) = \sum_{j=0}^n \left(\sum_{k=0}^{n-j} z_j w_{k}\right) = \sum_{j=0}^n z_j \sum_{k=0}^{n-j} w_{k}.
\end{equation*}

Por lo que:
\begin{align*}
C_n = \sum_{j=0}^n c_j = \sum_{j=0}^n z_j b_{n-j} & = \sum_{j=0}^n z_j\left(B-(B-b_{n-j})\right)\\
& = \sum_{j=0}^n z_j B – \sum_{j=0}^n z_j (B-b_{n-j})\\
& = a_n B – \sum_{j=0}^n z_j (B-b_{n-j}).
\end{align*}

Dado que $\lim\limits_{n\to\infty} a_n B = AB$, entonces solo resta probar que:
\begin{equation*}
\lim\limits_{n\to\infty} \sum_{j=0}^n z_j (B-b_{n-j}) = 0.
\end{equation*}

Sea $\varepsilon>0$. Como $\lim\limits_{n\to\infty} b_n = B$, entonces $\lim\limits_{n\to\infty} (b_n – B) = 0$. Por lo que, proposición 8.1, la sucesión $\left\{b_n – B\right\}_{n\geq 0}$ es acotada, es decir, existe $M>0$ tal que $|b_n -B| \leq M$ para toda $n\in\mathbb{N}$.

Dado que la serie $\sum_{n=0}^\infty |z_n|$ es convergente, para $\varepsilon/2M >0$ tenemos que existe $N_1\in\mathbb{N}$ tal que si $n\geq N_1$, entonces:
\begin{equation*}
\sum_{j=N_1 + 1}^\infty |z_j| = \left|\sum_{j=0}^n |z_j| – \sum_{j=0}^\infty |z_j|\right| < \frac{\varepsilon}{2M}.
\end{equation*}

Supongamos que $\sum_{n=0}^\infty |z_n| < \alpha$, con $\alpha > K \geq 0$. Como $\lim\limits_{n\to\infty} b_n = B$, para $\varepsilon/2\alpha >0$ tenemos que existe $N_2\in\mathbb{N}$ tal que si $n\geq N_2$, entonces:
\begin{equation*}
\left|b_n – B\right| < \frac{\varepsilon}{2\alpha}.
\end{equation*}

Sea $N \geq N_1 + N_2$. Notemos que para $j \leq N_1$, se cumple que $N – j \geq N_2$. Entonces, para toda $n\geq N$ tenemos que:
\begin{align*}
\left| \sum_{j=0}^n z_j (B-b_{n-j}) \right| & = \left| \sum_{j=0}^{N_1} z_j (B-b_{n-j}) + \sum_{j= N_1 + 1}^n z_j (B-b_{n-j})\right|\\
& \leq \sum_{j=0}^{N_1} |z_j| |B-b_{n-j}| + \sum_{j= N_1 + 1}^n |z_j| |B-b_{n-j}|\\
& \leq \frac{\varepsilon}{2\alpha} \sum_{j=0}^{N_1} |z_j| + M \sum_{j= N_1 + 1}^n |z_j|\\
& < \left(\frac{\varepsilon}{2\alpha}\right) \alpha + M \left(\frac{\varepsilon}{2 M}\right)\\
& =\varepsilon.
\end{align*}

Entonces:
\begin{equation*}
\lim_{n\to \infty} C_n = \lim_{n\to \infty} \sum_{j=0}^n c_j = \lim_{n\to \infty} \left(a_n B – \sum_{j=0}^n z_j (B-b_{n-j})\right) = AB,
\end{equation*}

de donde se sigue que el producto de Cauchy de las series es convergente y se cumple que:
\begin{equation*}
\sum_{n=0}^\infty c_n = \left(\sum_{n=0}^\infty z_n\right)\left(\sum_{n=0}^\infty w_n\right).
\end{equation*}

$\blacksquare$

Definición 27.6. (Sucesiones y series doblemente infinitas.)
Una sucesión de números complejos doblemente infinita es una función $f:\mathbb{Z}\to\mathbb{C}$ tal que a cada $n\in\mathbb{Z}$ asigna de manera única un número complejo. Si $f(n) = z_n \in \mathbb{C}$ para todo $n\in\mathbb{Z}$, entonces denotamos a la sucesión de números complejos doblemente infinita como $\left\{z_n\right\}_{n\in\mathbb{Z}}$ ó $\left\{z_n\right\}_{n=-\infty}^\infty$.

Una serie de números complejos doblemente infinita es una expresión de la forma:
\begin{equation*}
\sum_{n=-\infty}^\infty z_n.
\end{equation*}

Definición 27.7. (Sumas parciales de una serie doblemente infinita.)
Dada una serie de números complejos doblemente infinita $\sum_{n=-\infty}^\infty z_n$, para cada par de números $n,m \in\mathbb{N}^+$ definimos la sucesión de sumas parciales de la serie como:
\begin{equation*}
s_{m,n} = \sum_{k=-m}^n z_k = z_{-m} + z_{-m+1} + \cdots + z_{n-1} + z_n.
\end{equation*}

Definición 27.8. (Serie doblemente infinita convergente.)
Diremos que una serie de números complejos doblemente infinita $\sum_{n=-\infty}^\infty z_n$ converge a $s\in\mathbb{C}$ si $s_{m,n} \to s$ conforme $m\to\infty$ y $n\to\infty$ de forma independiente, es decir, si para todo $\varepsilon>0$ existe $N(\varepsilon)\in\mathbb{N}^+$ tal que si $m\geq N$ y $n\geq N$, entonces:
\begin{equation*}
|s_{m,n} – s| = \left| \sum_{k=-m}^n z_k – s \right| < \varepsilon.
\end{equation*}

En tal caso, denotaremos la convergencia de la serie a $s$ como $s = \sum_{n=-\infty}^\infty z_n$. En caso de no existir $s\in\mathbb{C}$ con tal propiedad, diremos que la serie de números complejos doblemente infinita es divergente.

Lema 27.1.
Una serie de números complejos doblemente infinita $\sum_{n=-\infty}^\infty z_n$ converge a $s = s^{-} + s^{+} \in\mathbb{C}$ si y solo si las series de números complejos $\sum_{n=0}^\infty z_n$ y $\sum_{n=1}^\infty z_{-n}$ convergen a $s^{+}$ y $s^{-}$, respectivamente. En tal caso:
\begin{equation*}
\sum_{n=-\infty}^\infty z_n = \sum_{n=1}^\infty z_{-n} + \sum_{n=0}^\infty z_n. \tag{27.3}
\end{equation*}

Demostración.
Sean $m\geq 1$ y $n\geq 1$, entonces las sucesiones de sumas parciales de cada serie están dadas por:
\begin{equation*}
s_{m,n} = \sum_{k=-m}^n z_k = z_{-m} + z_{-m+1} + \cdots + z_{n-1} + z_n,
\end{equation*}
\begin{equation*}
s_{-m} = \sum_{k=-m}^{-1} z_k = z_{-m} + z_{-m+1} + \cdots + z_{-2} + z_{-1},
\end{equation*}
\begin{equation*}
s_{n} = \sum_{k=0}^n z_k = z_{0} + z_{1} + \cdots + z_{n-1} + z_n,
\end{equation*} de donde $s_{m,n} = s_{-m} + s_{n}$.

$(\Longleftarrow$

Supongamos que $s^{-} = \sum_{n=1}^\infty z_{-n}$ y $ s^{+} = \sum_{n=0}^\infty z_n$, con $s^{-}, s^{+} \in \mathbb{C}$, es decir que ambas series son convergentes.

Entonces, por la proposición 27.2 es claro que si $m\to\infty$ y $n\to\infty$ entonces $s_{m,n} = s_{-m} + s_{n} \to s^{-} + s^{+}$, por lo que la serie $\sum_{n=-\infty}^\infty z_n$ converge y se cumple (29.3).

$\Longrightarrow)$

Supongamos que la serie $\sum_{n=-\infty}^\infty z_n$ converge a $s \in \mathbb{C}$.

Probaremos que la serie $\sum_{n=0}^\infty z_n$ converge utilizando el criterio de Cauchy. La convergencia de la serie restante es análoga y se deja como ejercicio al lector.

Sea $\varepsilon>0$. De acuerdo con la definición 27.7 tenemos que existe $M\in\mathbb{N}^+$ tal que si $p\geq M$ y $q\geq M$, con $p,q\in\mathbb{N}^{+}$, entonces $|s_{p,q} – s| < \varepsilon/2$. En particular $|s_{M,q} – s| < \varepsilon/2$ si $q\geq M$. Sea $N = M+1$, entonces para $n,m\geq N$, con $n>m$, por la desigualdad del triángulo tenemos que:
\begin{equation*}
\left|\sum_{k=m+1}^n z_k\right| = |s_{M,n} – s_{M,m}| \leq |s_{M,n} – s| + |s – s_{M,m}| < \frac{\varepsilon}{2} + \frac{\varepsilon}{2} = \varepsilon.
\end{equation*}

Por lo que, de acuerdo con la proposición 27.1, tenemos que la serie $\sum_{n=0}^\infty z_n$ converge.

De acuerdo con la primera parte de la prueba, como las series $\sum_{n=1}^\infty z_{-n}$ y $\sum_{n=0}^\infty z_n$ convergen, entonces se cumple (27.3).

$\blacksquare$

Observación 27.6.
De acuerdo con el lema anterior, es común definir la convergencia de una serie de números complejos doblemente infinita $\sum_{n=-\infty}^\infty z_n$, en función de la convergencia de las series $\sum_{n=1}^\infty z_{-n}$ y $\sum_{n=0}^\infty z_n$, en cuyo caso se dice que la serie doblemente infinita converge a la suma de ambas series dada en (27.3).

Ejemplo 27.14.
Analicemos el comportamiento de la serie $\sum_{n=-\infty}^\infty 2^{-|n|} z^n$.

Solución. De acuerdo con el lema 27.1, podemos analizar la convergencia de la serie doblemente infinita al separarla en dos series, dadas por $n\geq 0$ y $n<0$.

Para $n\geq 0$ tenemos que:
\begin{equation*}
\sum_{n=0}^\infty 2^{-|n|} z^n = \sum_{n=0}^\infty \frac{z^n}{2^{|n|}} = \sum_{n=0}^\infty \left(\frac{z}{2}\right)^n = \frac{1}{1-\dfrac{z}{2}} = \frac{2}{2-z},
\end{equation*} si $|z/2| < 1$, es decir si $|z|<2$. Mientras que la serie diverge si $|z|\geq 2$.

Por otra parte, para $n<0$ tenemos que:
\begin{align*}
\sum_{n=-\infty}^{-1} 2^{-|n|} z^n = \sum_{n=1}^\infty 2^{-|-n|} z^{-n} = \sum_{n=1}^\infty \frac{1}{z^n \, 2^{|n|}}
& = \sum_{n=1}^\infty \left(\frac{1}{2z}\right)^n\\
& = \left(\frac{1}{2z}\right) \sum_{n=1}^\infty \left(\frac{1}{2z}\right)^{n-1}\\
& = \left(\frac{1}{2z}\right) \sum_{k=0}^\infty \left(\frac{1}{2z}\right)^{k}\\
& = \left(\frac{1}{2z}\right) \left(\frac{1}{1-\dfrac{1}{2z}}\right)\\
&= \frac{1}{2z-1},
\end{align*} si se cumple que $|1/(2z)| < 1$, es decir si $|z|>1/2$. Mientras que la serie diverge en otro caso.

Entonces, de acuerdo con el lema 27.1, para los $z\in\mathbb{C}$ tales que $1/2 < |z| < 2$, tenemos que la serie converge y en tal caso:
\begin{equation*}
\sum_{n=-\infty}^\infty 2^{-|n|} z^n = \frac{2}{2-z} + \frac{1}{2z-1} = \frac{3z}{(2-z)(2z-1)}.
\end{equation*}

Podemos visualizar la región de convergencia y los valores que toma la serie en el siguiente Applet de GeoGebra: https://www.geogebra.org/m/eqjzzthz.

Tarea moral

1. Completa la demostración de la proposición 27.2.
2. Prueba el corolario 27.4.
3. Prueba que si una serie $\displaystyle \sum_{n=0}^\infty z_n$ converge, entonces $\lim\limits_{m\to\infty} \displaystyle \sum_{n=m+1}^\infty z_n = 0$, es decir, si la serie converge entonces su cola tiende a $0$.
4. Muestra que:
   a) $\displaystyle \sum_{n=0}^\infty \dfrac{1}{(2+i)^n} = \dfrac{3-i}{2}$.
   b) $\displaystyle \sum_{n=0}^\infty \left(\dfrac{1}{n+1+i} – \dfrac{1}{n+i}\right) = i$.
   c) $\displaystyle \sum_{n=0}^\infty \dfrac{(1+i)^n}{2^n} = 1+i$.
   d) $\displaystyle \sum_{n=0}^\infty \dfrac{(1-i)^n}{2^n} = 1-i$.
5. Prueba que las siguientes series convergen.
   a) $\displaystyle \sum_{n=1}^\infty \dfrac{(3+4i)^n}{5^n n^2}$.
   b) $\displaystyle \sum_{n=1}^\infty \left(\dfrac{1}{n+2i} – \dfrac{1}{n+1+2i}\right)$.
   c) $\displaystyle \sum_{n=1}^\infty \dfrac{i}{n(n+1)}$.
   d) $\displaystyle \sum_{n=0}^\infty \dfrac{(1+i)^{2n}}{(2n+1)!}$.
6. Utiliza la serie geométrica para determinar la mayor región de convergencia de las siguientes series y obtén el valor de cada suma.
   a) $\displaystyle \sum_{n=0}^\infty\left[\left(\dfrac{2}{z}\right)^n + \left(\dfrac{z}{3}\right)^n\right]$.
   b) $\displaystyle \sum_{n=0}^\infty \left(\dfrac{(3+i)z}{4-i}\right)^n$.
   c) $\displaystyle \sum_{n=1}^\infty\left(1 + z\right)^n$.
   d) $\displaystyle \sum_{n=0}^\infty \dfrac{2^{n+1}}{(2+i-z)^n}$.
7. Sean $r,\theta\in\mathbb{R}$, con $0\leq r < 1$. Muestra que:
   a) $\displaystyle \sum_{n=0}^\infty r^n e^{i n\theta} = \dfrac{1}{1-re^{i \theta}}$.
   b) $\displaystyle \sum_{n=-\infty}^\infty r^{|n|} e^{i n\theta} = \dfrac{1}{1-re^{- i \theta}} + \dfrac{re^{i \theta}}{1-re^{i \theta}}$.
   c) $\displaystyle \sum_{n=0}^\infty r^n \operatorname{cos}(n\theta) = \dfrac{1-r\operatorname{cos}(\theta)}{1+r^2-2r\operatorname{cos}(\theta)}$.
   d) $\displaystyle \sum_{n=0}^\infty r^n \operatorname{sen}(n\theta) = \dfrac{r\operatorname{sen}(\theta)}{1+r^2-2r\operatorname{cos}(\theta)}$.
8. Sean $\sum_{n=0}^\infty z_n $ y $\sum_{n=0}^\infty z_n^2$ dos series convergentes, de números complejos tales que $\operatorname{Re}(z_n)\geq 0$, para todo $n\in\mathbb{N}$. Prueba que la serie $\sum_{n=0}^\infty|z_n|^2$ es convergente.
9. Muestra que: \begin{equation*} \displaystyle \sum_{n=1}^\infty \frac{n(n+1)}{2} z^{n-1} = \frac{1}{(1-z)^3}. \end{equation*} Hint: Considera el resultado del ejemplo 27.13 y utiliza la identidad $\displaystyle\sum_{k=1}^n k = \dfrac{n(n+1)}{2}$.
10. Determina para qué valores de $z\in\mathbb{C}$ la serie $\displaystyle \sum_{n=0}^\infty e^{inz}$ converge, es decir, su región de convergencia.
    Hint: Considera la serie geométrica.

Más adelante…

En esta entrada hemos dado la definición de serie, desde el sentido complejo, y probamos algunos resultados elementales para estudiar la convergencia de una serie, los cuales nos serán de utilidad en las siguientes entradas.

Al igual que con muchos otros conceptos, las definiciones y criterios obtenidos para las series de números complejos son muy similares a los que estudiamos en nuestros cursos de Cálculo para las series de números reales.

La siguiente entrada abordaremos los conceptos de sucesión y serie de funciones complejas, así como los conceptos de convergencia puntual y uniforme. Además de obtener algunos resultados elementales en el estudio de las series de funciones complejas.

Entradas relacionadas

• Ir a Variable Compleja I.
• Entrada anterior del curso: Funciones complejas como transformaciones. Técnicas de graficación.
• Siguiente entrada del curso: Sucesiones y series de funciones.