Archivo de la etiqueta: Teorema de Cauchy

Álgebra Moderna I: $p$ -Subgrupo de Sylow y el Normalizador de $H$ en $G$

Por Cecilia del Carmen Villatoro Ramos

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Cuando nació la Teoría de grupos uno de los problemas principales fue clasificar a los grupos finitos. Una manera de estudiar este problema es empezar por entender un tipo especial de grupos finitos: grupos con orden primo $p$ , llamemos $G$ a este grupo. El estudio de $G$ se hace más sencillo pues sabemos que es un grupo cíclico y es isomorfo a $Z_{p} .$

Podemos aumentar la dificultad y considerar el caso cuando $| G | = p^{t}$ , con $p$ primo y $t \in N .$ Pero, ¿qué sucede si $G$ no es un $p$ -grupo? Supongamos que $| G | = n = p^{t} m$ donde $t \in N$ y $p$ no divide a $m .$

Dibujo de la representación de un $p$ -grupo de Sylow

En esta entrada lo que haremos será intentar estudiar a un grupo cualquiera $G$ a partir de los $p$ -grupos que lo conforman, que serán llamados $p$ -subgrupos de $G$ . Estos subgrupos pueden estar contenidos a su vez en otros $p$ -subgrupos o bien ser máximos con respecto a la contención y no estar contenidos en ningún otro $p$ -subgrupo. A estos $p$ -subgrupos máximos se les llama $p$ -subgrupos de Sylow de $G$ .

Estudiar todos los $p$ -subgrupos de Sylow de $G$ para los primos que dividen al orden de $G$ nos ayuda a entender cómo es el mismo $G .$

Comencemos con subgrupos de Sylow

Definición. Sea $p \in Z^{+}$ un primo, $G$ un grupo finito. Decimos que $P$ es un $p$ -subgrupo de $G$ si el orden de $P$ es una potencia de $p$ . Además, decimos que $P$ es un $p$ -subgrupo de Sylow de $G$ si

$P$ es un $p$ -grupo;
si $Q$ es un $p$ -grupo con $P \subseteq Q \subseteq G$ , entonces $P = Q$ .

Es decir $P$ es un $p$ -subgrupo de $G$ máximo con respecto a la contención.

Observación. Siempre existe los subgrupos de Sylow.

Demostración.
Sea $p \in Z^{+}$ un primo, $G$ un grupo finito con $| G | = n$ .

Si $p ⧸ | n$ , entonces ${e}$ es un $p$ -subgrupo de Sylow.

Si $p | n$ , por el teorema de Cauchy existe $g \in G$ de orden $p$ . Si $⟨ g ⟩$ no es $p$ -subgrupo de Sylow, entonces existe $Q_{1} \leq G$ $p$ -subgrupo con $⟨ g ⟩ ⊈ Q_{1} .$ Si $Q_{1}$ no es un $p$ -subgrupo de Sylow debe existir $Q_{2} \leq G$ $p$ -subgrupo con $Q_{1} ⊈ Q_{2} .$ Continuando de este modo, dado que $G$ es de orden finito y $1 < | ⟨ g ⟩ | < | Q_{1} | < | Q_{2} | < \dots < | G |$ obtenemos un $p$ -subgrupo de Sylow después de un número finito de pasos.

Ejemplos

Ejemplo 1. Sea $G = S_{4}$ , $| S_{4} | = 4! = 24 = 2^{3} \cdot 3$ .
Entonces hay dos primos involucrados en $| S_{4} |$ , estos son 2 y 3.

$⟨ (1 2 3) ⟩$ es un $3$ -subgrupo de $S_{4}$ . Como no hay otra potencia de 3 que divida a $| S_{4} |$ , no hay grupos de orden 9,27, etc. por lo que $⟨ (1 2 3) ⟩$ es un $3$ -subgrupo de Sylow de $S_{4}$

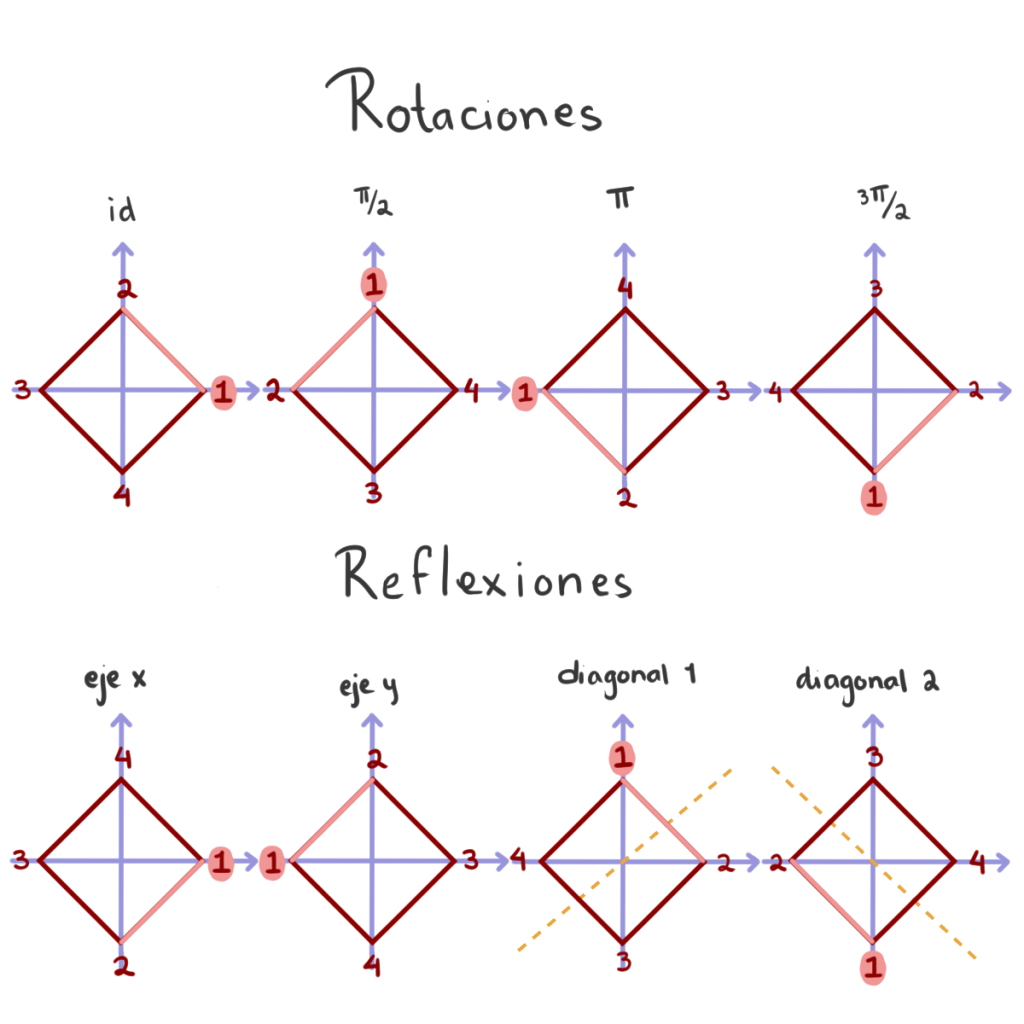
Por otro lado, para los $2$ -subgrupos de Sylow podríamos tener subgrupos de orden $2$ , $4$ y hasta $8$ . De una manera intuitiva sabemos que podemos ver a $S_{4}$ como todas las simetrías de un cuadrado.

Notemos que no todas las permutaciones de los vértices de un cuadrado son simetrías, pero todas las simetrías de un cuadrado se pueden ver como permutaciones de sus vértices. Las permutaciones que también son simetrías son: las rotaciones por 90 grados, las reflexiones por los ejes y las reflexiones por las diagonales.

La rotación de $90$ grados, que corresponde a la permutación $(1 2 3 4),$ y la reflexión por el eje $x,$ que corresponde a la transposición $(2 4)$ , generan al grupo diédrico. Por lo que $⟨ (1 2 3 4), (2 4) ⟩$ es isomorfo al grupo diédrico $D_{2 (4)}$ que es de orden $8$ . Así, $⟨ (1 2 3 4), (2 4) ⟩$ es un $2$ -subgrupo de Sylow de $S_{4}$ de orden 8.

Ejemplo 2. Sea $G = A_{4}$ , $| A_{5} | = 60 = 2^{2} \cdot 3 \cdot 5$ .

Consideremos el grupo de Klein ${(1), (1 2) (3 4), (1 3) (2 4), (1 4) (2 3)}$ que es un subgrupo de $A_{5}$ de orden $4$ y por lo tanto un $2$ -subgrupo de Sylow de $A_{5}$ .

El subgrupo anterior se hizo considerando todas las permutaciones que son productos de dos transposiciones disjuntas de los números $1$ , $2$ , $3$ y $4$ , si ahora hacemos lo mismo pero considerando todas las permutaciones que son productos de dos transposiciones disjuntas de los números $2$ , $3$ , $4$ y $5$ obtenemos ${(1), (2 3) (4 5), (2 4) (3 5), (2 5) (3 4)}$ que es otro $2$ -subgrupo de Sylow de $A_{5}$ . Siguiendo de esta manera podríamos construir distintos $2$ -subgrupos de Sylow.

Si nos tomamos un $3$ -ciclo y su generado obtenemos un $3$ -subgrupo de Sylow de $A_{5}$ , por ejemplo $⟨ (1 2 3) ⟩$ es un $3$ -subgrupo de Sylow de $A_{5}$ . Notamos que podemos elegir $3$ -ciclos distintos de $(1 2 3)$ y de su inverso y con ello crear diferentes $3$ -subgrupos de Sylow de $A_{5}$ .

Si tomamos un $5$ -ciclo y su generado obtenemos un $5$ -subgrupo de Sylow de $A_{5}$ , por ejemplo $⟨ (1 2 3 4 5) ⟩$ es un $5$ -subgrupo de Sylow de $A_{5}$ . Pero también podemos tomar un $5$ -ciclo que no esté en el generado $⟨ (1 2 3 4 5) ⟩$ y obtener otro $5$ - subgrupo de Sylow de $A_{5}$ .

Últimos preparativos

Definición. Sea $G$ un grupo, $H$ subgrupo de $G$ . El normalizador de $H$ en $G$ es
$\begin{array}{r} N_{G} (H) = {g \in G | g H g^{- 1} = H} . \end{array}$

Representación del normalizador de $H$ en $G$ .
Observemos que un elemento $g$ del normalizado de $H$ no necesariamente está en $H$ .

Observación. Por construcción $H ⊴ N_{G} (H)$ .

Lema. Sea $p \in Z^{+}$ un primo, $G$ un grupo finito, $H$ un $p$ -subgrupo de $G$ . Entonces
$\begin{array}{r} [N_{G} (H) : H] \equiv [G : H] (mód p) . \end{array}$

Demostración.
Sean $p \in Z^{+}$ un primo, $G$ un grupo finito y $H$ un $p$ -subgrupo de $G$ . Consideremos $X = {g H | g \in G}$ y la acción de $H$ en $X$ dada por
$\begin{array}{r} h \cdot (g H) = h g H \forall h \in H, \forall g \in G . \end{array}$

Como $H$ es un $p$ -grupo, de acuerdo al último teorema de la entrada Clase de Conjugación, Centro de $G$ , Ecuación de Clase y $p$ -Grupo sabemos que
$\begin{array}{r} [G : H] = # X \equiv # X_{H} (mód p) . \end{array}$

Pero
$\begin{aligned} X_{H} & = {g H \in X | h \cdot (g H) = g H \forall h \in H} \\ = {g H \in X | h g H = g H \forall h \in H} \\ = {g H \in X | g^{- 1} h g \in H \forall h \in H} \\ = {g H \in X | g^{- 1} H g \subseteq H} \\ = {g H \in X | g^{- 1} H g = H} & pues G es finito y en consecuencia H también. \\ = {g H | g \in N_{G} (H)} \\ = N_{G} (H) / H . \end{aligned}$

Así, $# X_{H} = [N_{G} (H) : H]$ y entonces $[G : H] \equiv [N_{G} (H) : H] (mód p) .$

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Encuentra los $2$ -subgrupos de los cuaternios $Q_{8} .$
Encuentra todos los $3$ -subgrupos del grupo simétrico $S_{4} .$ Etiquetando los vértices del cuadrado de maneras distintas a la que viene en el ejemplo 2 de esta entrada, encuentra la mayor cantidad que puedas de $2$ -subgrupos de Sylow de $S_{4}$ .
Sea $P$ un $p$ -subgrupo de Sylow de un grupo finito $G$ . Prueba que:
- Cada conjugado de $P$ también es un $p$ -subgrupo de Sylow.
- $p$ no divide a $| N_{g} (P) / P |$ .
- Si $g \in G$ es tal que $o (g) = p^{m}$ para alguna $m \in Z^{+}$ y si $g P g^{- 1} = P$ , entonces $g \in P .$

Más adelante…

¡Ahora sí! Todo está listo para que en la siguiente entrada estudiemos los tres Teoremas de Sylow. Te adelanto que todos los Teoremas de Sylow se sirven de los $p$ -subgrupos que vimos en esta entrada. De hecho, los relaciona con los temas que hemos visto como subgrupo normal y conjugados.

Entradas relacionadas

Ir a Álgebra Moderna I.
Entrada anterior del curso: Teorema de Cauchy.
Siguiente entrada del curso: Teoremas de Sylow.
Resto de cursos: Cursos.

Álgebra Moderna I: Teorema de Cauchy

Por Cecilia del Carmen Villatoro Ramos

2 respuestas

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Hemos llegado a uno de los resultados más importantes del curso: el Teorema de Cauchy. Éste nos asegura la existencia de un elemento de determinado orden en el grupo. De forma más precisa nos dice que para cada primo que divida al orden del grupo, existe un elemento con orden exactamente ese primo.

Con este resultado nos nace una nueva pregunta: ¿cómo se relaciona esto con los $p$ -grupos? y otra más: ¿se puede relacionar esto con el centro de un grupo? Tal vez no parezcan preguntas que te harías directamente después de ver el teorema, pero igual las responderemos. Es especialmente interesante lo del centro de un grupo porque en ocasiones podemos concluir que ciertos grupos deben ser abelianos.

Uno de los resultados más importantes del curso

Teorema de Cauchy.
Sea $G$ un grupo finito, $p \in Z^{+}$ un primo que divida a $| G | .$ Entonces existe $g \in G$ de orden $p .$

Demostración.
Sea $G$ un grupo finito, $p \in Z^{+}$ un primo tal que $p | | G | .$

P.D. Existe un elemento $g \in G$ de orden $p$ .

Para esta demostración, queremos usar el último teorema de la entrada anterior. Pero este sólo aplica para un conjunto finito y un $p$ -grupo. Por lo que comenzaremos definiendo un conjunto finito a partir de $G$ .

Consideremos
$\begin{array}{r} X = {(g_{1}, \dots, g_{p}) | g_{1}, \dots, g_{p} \in G, g_{1} \dots g_{p} = e} \end{array}$
el conjunto de las $p -$ adas cuyo producto dé el neutro.

Observemos que podemos elegir las primeras $p - 1$ entradas de un elemento en $X$ como sea, pero la última no porque la condición $g_{1} \dots g_{p} = e$ nos indica que $g_{p} = (g_{1} \dots g_{p - 1})^{- 1} .$ Así $# X = | G |^{p - 1}$ y como $p$ divide al orden de $G$ , entonces $p | # X$ .

Sea $H = ⟨ (1 2 \dots p) ⟩ \leq S_{p}$ , el cual es un $p$ -grupo. $H$ actúa en $X$ permutando los subíndices, es decir,
$\begin{array}{r} (1 2 \dots p) \cdot (g_{1}, \dots, g_{p}) = (g_{2}, g_{3}, \dots, g_{p}, g_{1}) \end{array}$
y en general, si $σ = (1 2 \dots p)$ , entonces para toda $j \in Z$
$\begin{array}{r} σ^{j} \cdot (g_{1}, \dots, g_{p}) = (g_{σ^{j} (1)}, \dots, g_{σ^{j} (p)}) . \end{array}$

Tenemos que observar que la acción está bien definida. Esto sucede ya que si $(g_{1}, \dots, g_{p}) \in X$ tenemos que $g_{1} = (g_{2}, \dots, g_{p})^{- 1}$ y así $(g_{2} \dots g_{p}) g_{1} = e .$

Entonces $(1 2 \dots p) \cdot (g_{1}, \dots, g_{p}) = (g_{2}, \dots, g_{p}, g_{1}) \in X .$ Así, $H$ manda elementos de $X$ en elementos de $X$ .

Por otro lado,
$\begin{array}{r} id \cdot (g_{1}, \dots, g_{p}) = (g_{id (1)}, \dots, g_{id(p)}) = (g_{1}, \dots, g_{p}) \end{array}$
y además
$\begin{aligned} σ^{j} \cdot (σ^{t} \cdot (g_{1}, \dots, g_{p})) & = σ^{j} \cdot (g_{σ^{t} (1)}, \dots, g_{σ^{t} (p)}) & Aplicamos σ^{t} \\ = (g_{σ^{j} (σ^{t} (1))}, \dots, g_{σ^{j} (σ^{t} (p))}) & Aplicamos σ^{j} \\ = (g_{σ^{j + t} (1)}, \dots, g_{σ^{j + t} (p)}) \\ = σ^{j + t} \cdot (g_{1}, \dots, g_{p}) = (σ^{j} σ^{t}) \cdot (g_{1}, \dots, g_{p}) . \end{aligned}$

Así, efectivamente tenemos una acción de $H$ en $X$ .

Como $| H | = p$ , por el teorema de la entrada anterior
$\begin{array}{r} # X \equiv # X_{H} (mód p) . \end{array}$
Pero recordemos que $p ∣ # X$ , entonces $p ∣ # X_{H} .$

Ahora vamos a analizar cómo es $# X_{H}$ . Comencemos por entender quién es el conjunto $X_{H}$ ,
$\begin{aligned} X_{H} & = {(g_{1}, \dots, g_{p}) \in X | σ^{j} \cdot (g_{1}, \dots, g_{p}) = (g_{1}, \dots, g_{p}) \forall j} \\ = {(g_{1}, \dots, g_{p}) \in X | σ \cdot (g_{1}, \dots, g_{p}) = (g_{1}, \dots, g_{p})} & si σ fija a un elemento, también σ^{j} \\ = {(g_{1}, \dots, g_{p}) \in X | (g_{2}, \dots, g_{p}, g_{1}) = (g_{1}, \dots, g_{p})} & Definición de σ \\ = {(g_{1}, \dots, g_{p}) \in X | g_{1} = \dots = g_{p}} & Implicación directa . \end{aligned}$

En particular, $(e, \dots, e) \in X_{H}$ por lo que $# X_{H} \geq 1$ . Pero no puede haber exactamente un elemento en $X_{H}$ porque $p | # X_{H}$ , entonces $# X_{H} > 1.$ Existe entonces $(g, \dots, g) \in X_{H}$ con $g \in G$ tal que $g \neq e .$

Como $(g, \dots, g) \in X$ se tiene que $g^{p} = g \dots g = e$ con $g \in G$ con $g \neq e .$

Así $g$ es un elemento en $G$ de orden $p$ .

Corolario. Sea $p \in Z^{+}$ un primo, $G$ un grupo finito. $G$ es un $p$ -grupo si y sólo si para todo $g \in G$ el orden $o (g)$ es una potencia de $p$ .

Proposición. Sea $p \in Z^{+}$ un primo. Si $G$ es un $p$ -grupo con $G \neq {e}$ (no trivial) entonces $Z (G) \neq {e} .$

Demostración.
Sea $p \in Z^{+}$ un primo, $G$ un $p$ -grupo con $G \neq {e} .$ Por la ecuación de clase
$\begin{array}{r} | G | = | Z (G) | + \sum_{j = 1}^{k} [G : C_{G} (x_{j})] \end{array}$
con $x_{1}, \dots, x_{k}$ representantes de las distintas clases de conjugación con más de un elemento, por lo que
$\begin{aligned} 1 < # x_{j}^{G} & = [G : C_{G} (x_{j})] = \frac{| G |}{| C_{G} |} | | G | . \end{aligned}$

Como $| G | = p^{t}$ , $t \in N$ , entonces $p | [G : C_{G} (x_{j})]$ para toda $j \in {1, \dots, k}$ .

Así
$\begin{array}{r} p | | G | - \sum_{j = 1}^{k} [G : C_{G} (x_{j})] = | Z (G) | . \end{array}$

Como $| Z (G) |$ es múltiplo de $p$ no nulo, no puede ser 1. Entonces $Z (G) \neq {e} .$

¿Grupos abelianos de nuevo?

Lema. Sea $G$ un grupo. Si $G / Z (G)$ es cíclico, entonces $G$ es abeliano.

Demostración.
Sea $G$ un grupo tal que $G / Z (G)$ es cíclico.

Entonces $G / Z (G) = ⟨ g Z (G) ⟩$ con $g \in G .$

Sean $a, b \in G$ . Como $a Z (G), b Z (G) \in G / Z (G) = ⟨ g Z (G) ⟩$ entonces
$\begin{aligned} a Z (G) & = g^{k} Z (G) \\ b Z (G) & = g^{t} Z (G) & con k, t \in Z . \end{aligned}$

Así,
$\begin{aligned} a & = g^{k} z_{1} \\ b & = g^{t} z_{2} & con k, t \in Z, z_{1}, z_{2} \in Z (G) . \end{aligned}$

Entonces
$\begin{aligned} a b & = (g^{k} z_{1}) (g^{t} z_{2}) = g^{k + t} z_{1} z_{2} & Como z_{1} \in Z (G), entonces z_{1} conmuta con g^{t} \\ b a & = (g^{t} z_{2}) (g^{k} z_{1}) = g^{t + k} z_{2} z_{1} & Como z_{2} \in Z (G), entonces z_{2} conmuta con g^{k} . \end{aligned}$

Así $a b = b a$ . Por lo tanto $G$ es abeliano.

Corolario. Sea $p \in Z^{+}$ un primo. Si $G$ es un grupo de orden $p^{2}$ , entonces $G$ es abeliano.

Demostración.
Sea $p \in Z^{+}$ un primo, $G$ un grupo con $| G | = p^{2}$ .

$G$ es entonces un $p$ -grupo con $G \neq {e}$ , por la proposición previa $Z (G) \neq {e} .$

Como $Z (G) \leq G$ , entonces $| Z (G) | | | G | = p^{2}$ , con $| Z (G) | \neq 1.$ Así que $| Z (G) | = p$ ó $| Z (G) | = p^{2} .$

Si $| Z (G) | = p,$ entonces
$\begin{array}{r} | G / Z (G) | = \frac{| G |}{| Z (G) |} = \frac{p^{2}}{p} = p, \end{array}$
entonces $G / Z (G)$ es cíclico. Por el lema se tiene que $G$ es abeliano y entonces $Z (G) = G$ . Esto es una contradicción porque $| G | = p^{2}$ y estamos suponiendo que $| Z (G) | = p$ .

En consecuencia, obtenemos que $| Z (G) | = p^{2}$ , entonces $Z (G) = G$ y así $G$ es abeliano.

Tarea moral

Demuestra el primer corolario de esta entrada: Sea $p \in Z^{+}$ un primo, $G$ un grupo finito. $G$ es un $p$ -grupo si y sólo si para todo $g \in G$ el orden $o (g)$ es una potencia de $p$ . (Sugerencia: Usa el Teorema de Cauchy).
Sea $p$ un primo, prueba que cada grupo $G$ de orden $2 p$ es cíclico o isomorfo a $D_{2 p} .$
Prueba o da un contraejemplo: Todo grupo de orden $p^{3}$ con $p \in Z^{+}$ un primo, es abeliano.
Demuestra que si $G$ es un $p$ -grupo finito no abeliano tal que $| G | = p^{3} .$ Entonces, $Z (G) ≅ Z_{p} .$

Más adelante…

Nos estamos encaminando a demostrar los Teoremas de Sylow, para ello todavía nos faltan un par de definiciones. En la siguiente entrada definiremos a los $p$ -subgrupos de Sylow y usaremos el Teorema de Cauchy para probar que estos subgrupos siempre existen.

Entradas relacionadas

Ir a Álgebra Moderna I.
Entrada anterior del curso: Clase de Conjugación, Centro de $G$ , Ecuación de Clase y $p$ -Grupo.
Siguiente entrada del curso: $p$ -Subgrupo de Sylow y el Normalizador de $H$ en $G$ .
Resto de cursos: Cursos.

El blog de Leo

Aprendiendo, creando y compartiendo matemáticas

Archivo de la etiqueta: Teorema de Cauchy

Álgebra Moderna I: $p$ -Subgrupo de Sylow y el Normalizador de $H$ en $G$

Introducción

Comencemos con subgrupos de Sylow

Ejemplos

Últimos preparativos

Tarea moral

Más adelante…

Entradas relacionadas

Álgebra Moderna I: Teorema de Cauchy

Introducción

Uno de los resultados más importantes del curso

¿Grupos abelianos de nuevo?

Tarea moral

Más adelante…

Entradas relacionadas