Archivo de la etiqueta: Polinomios de Taylor

Cálculo Diferencial e Integral I: Polinomios de Taylor (Parte 2)

Por Karen González Cárdenas

Deja un comentario

Introducción

En la entrada anterior vimos que el polinomio de Taylor para una función $f$ que se puede derivar $n$ veces en $x=a$, es:
$$T_{a,n}=\sum_{j=0}^{n} \frac{f^{(j)}(a)}{j!}(x-a)^{j}.$$

Además vimos que cumplía con la siguiente igualdad:
$$\lim_{x\to a}\frac{f(x)-T_{a,n}(x)}{(x-a)^{n}}=0$$

que nos indicaba que el polinomio de Taylor es una buena aproximación de la función $f$.

Pero, ¿qué podemos decir de la diferencia $ f(x)-T_{a,n}(x)$? ¿Cuáles son las propiedades que cumple?

A lo largo de esta entrada veremos que dicha diferencia es llamada Residuo de Taylor y que existen un par de formas de escribirlo. También veremos un ejemplo donde se nos pedirá estimar dicho residuo dependiendo del polinomio de Taylor considerado.

Definición del Residuo de Taylor

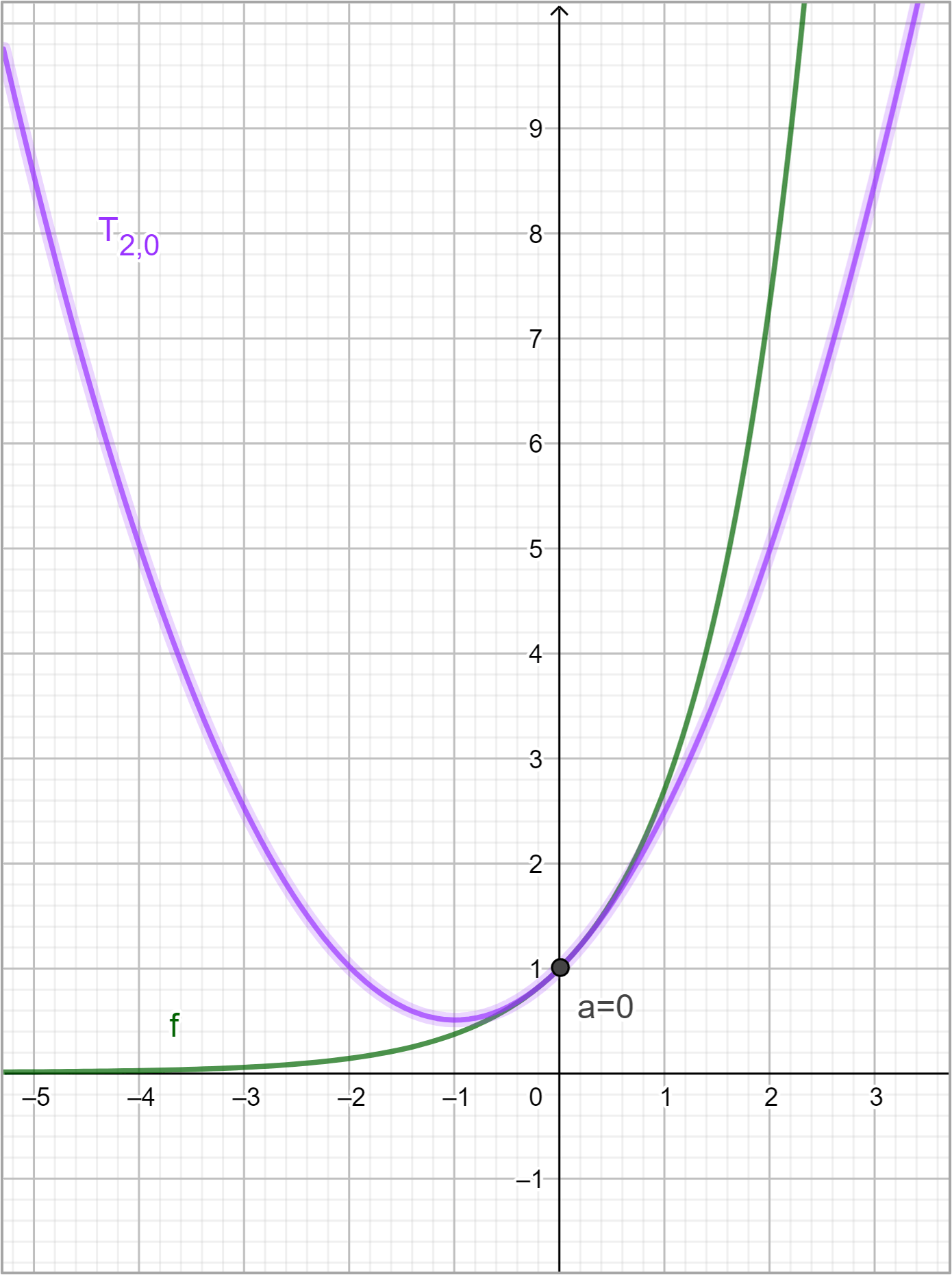
Retomando uno de los ejemplos anteriores:

En esta imagen vemos que el polinomio de Taylor $T_{2,0}$ se parece mucho a la función $f$ cuando $a=0$, sin embargo, sigue existiendo una diferencia o «error» ya que el polinomio y $f$ no son «idénticas». A dicho error se le conoce formalmente como Residuo de Taylor, veamos su definición:

Definición (Residuo de Taylor): Consideremos una función $f: [x_0,y_0] \rightarrow \r$ de clase $C^{(n)}$. Definiremos al Residuo de Taylor de grado $n$ con centro en $a$ como:
$$R_{n,a}:[x_0,y_0] \rightarrow \r$$
$$R_{n,a}(x)=f(x)-T_{n,a}(x).$$

Nota: Recordemos que una función es de clase $C^{(n)}$ si es $n$ veces derivable y sus $n$ derivadas son continuas.

Vemos que de la definición anterior tenemos que al realizar una aproximación usando polinomios de Taylor para una función $f$ se da la siguiente igualdad :
$$f(x)=T_{n,a}(x)+R_{n,a}(x).$$

Y además si sustituimos $ R_{n,a}(x)=f(x)-T_{n,a}(x)$ en el siguiente límite:
$$ \lim_{x\to a}\frac{f(x)-T_{n,a}(x)}{(x-a)^{n}}=0.$$

Concluimos que:

$$\lim_{x\to a}\frac{R_{n,a}(x)}{(x-a)^{n}}=0.$$

Reescribiendo tenemos que podemos hallar al polinomio de Taylor para una función $f$ considerando:
$$f(x)=T_{n,a}(x)+(x-a)^{n}R^{*}_{n,a}(x)$$
donde $R^{*}_{n,a}(x) = \frac{R_{n,a}(x)}{(x-a)^{n}}$ y el residuo cuando $x$ tiende a $a$ es cero:
$$\lim_{x \to a}R^{*}_{n,a}(x)=0$$

¿De qué forma podemos escribir el Residuo de Taylor?

En el siguiente teorema veremos dos maneras distintas para el residuo: la de Cauchy y la de Lagrange.

Teorema: Consideremos una función $f: [x_0,y_0] \rightarrow \r$ donde $f$ es $n+1$ veces derivable en $(x_0,y_0)$, un punto $a\in [x_0,y_0]$ y un $x \in (x,y_0]$. Entonces existe $t\in (a,x)$ tal que:

  1. $$R_{n,a}(x)=\frac{f^{(n+1)}(t)}{n!}(x-t)^{n}(x-a)$$
    que es la forma del residuo de Cauchy.
  2. $$R_{n,a}(x)=\frac{f^{(n+1)}(t)}{(n+1)!}(x-a)^{n+1}$$
    que es la forma del residuo de Lagrange.

Demostración: Para realizar la prueba de los dos puntos del teorema veremos primero cuál es la derivada del residuo $R_{n,t}$. Por ello consideraremos a la función $Q: [a,x] \rightarrow \r$ como sigue:
\begin{align*}
Q(t)&=R_{n,t}(x)\\
&=f(x)-T_{n,t}(x)\tag{por definición de residuo}\\
&=f(x)-\sum_{j=0}^{n}\frac{f^{(j)}(t)}{j!}(x-t)^{j} \tag{por definición de Taylor}
\end{align*}
Cabe mencionar que estamos considerando fija a $x$.

Observemos lo siguiente, a estos puntos los llamaremos $(*)$ :

  • \begin{align*}
    Q(x)&=f(x)-T_{n,x}(x)\\
    &=f(x)-f(x)\\
    &=0
    \end{align*}
  • $$Q(a)=R_{n,a}(x)$$

Ahora si derivamos a $Q(t)$ respecto de $t$ obtenemos:
\begin{align*}
\dfrac{dQ}{dt}(t)&=0- \sum_{j=0}^{n}\left( \frac{f^{(j+1)}(t)}{j!}(x-t)^{j}- \frac{f^{(j)}(t)}{j!}j (x-t)^{j-1}\right)\\
&=- \sum_{j=0}^{n}\left( \frac{f^{(j+1)}(t)}{j!}(x-t)^{j}-\frac{f^{(j)}(t)}{(j-1)!}(x-t)^{j-1}\right)\\
&=- \left(f^{(1)}(t)(1)-0+f^{(2)}(t)(x-t)-f^{(1)}(t)+\frac{f^{(3)}(t)}{2!}(x-t)^{2}-f^{(2)}(t)(x-t)+\ldots+ \frac{f^{(n+1)}(t)}{n!}(x-t)^{n}-\frac{f^{(n)}(t)}{(n-1)!}(x-t)^{n-1}\right)
\end{align*}

Observamos que los términos se van cancelando, ya que va apareciendo alternadamente positivos y negativos:
\begin{align*}
& =- \left(\cancel{f^{(1)}(t)(1)}-0+f^{(2)}(t)(x-t)-\cancel{f^{(1)}(t)}+\frac{f^{(3)}(t)}{2!}(x-t)^{2}-f^{(2)}(t)(x-t)+\ldots+ \frac{f^{(n+1)}(t)}{n!}(x-t)^{n}-\frac{f^{(n)}(t)}{(n-1)!}(x-t)^{n-1}\right)\\
& =- \left(\cancel{f^{(2)}(t)(x-t)}+\frac{f^{(3)}(t)}{2!}(x-t)^{2}-\cancel{f^{(2)}(t)(x-t)}+\ldots+ \frac{f^{(n+1)}(t)}{n!}(x-t)^{n}-\frac{f^{(n)}(t)}{(n-1)!}(x-t)^{n-1}\right)\\
\end{align*}

Si continuamos cancelando los términos, notamos que el único que nos queda es:
\begin{align*}
&=- \frac{f^{(n+1)}(t)}{n!}(x-t)^{n}
\end{align*}

Concluimos que:
$$Q'(t)=- \frac{f^{(n+1)}(t)}{n!}(x-t)^{n} $$
A la igualdad anterior la llamaremos $(**)$.

Pasemos a probar los puntos $1.$ y $2.$:

  1. Aplicaremos el Teorema del valor medio para la derivada en el intervalo $[a,x]$, así tenemos que existe un $t\in [a,x]$ tal que.
    $$Q'(t)=\frac{Q(x)-Q(a)}{x-a}$$
    Por las observaciones $(*)$ y $(**)$ tendríamos la siguiente igualdad:
    $$-\frac{f^{(n+1)}(t)}{n!}(x-t)^{n}=\frac{0-R_{n,a}(x)}{x-a}$$
    De lo anterior, al simplificar nos queda:
    $$R_{n,a}(x)=\frac{f^{(n+1)}(t)}{n!}(x-t)^{n}(x-a)$$
  2. Ahora usaremos el Teorema del valor medio generalizado o de Cauchy, si tomamos $g(t)=(x-t)^{n+1}$ entonces existe un $t\in (a,x)$ tal que:
    \begin{align*}
    (Q(x)-Q(a))g'(t)=(g(x)-g(a))Q'(t)&\Rightarrow \frac{Q(x)-Q(a)}{g(x)-g(a)}=\frac{Q'(t)}{g'(t)}
    \end{align*}
    Así por $(**)$ ocurre que:
    \begin{align*}
    \frac{Q(x)-Q(a)}{g(x)-g(a)}&=\frac{-\frac{f^{(n+1)}(t)}{n!}\cancel{(x-t)^{n}}}{-(n+1)\cancel{(x-t)^{n}}}\\
    &=\frac{f^{(n+1)}(t)}{n!(n+1)}\\
    &=\frac{f^{(n+1)}(t)}{(n+1)!}
    \end{align*}
    Si ahora consideramos las observaciones dadas en $(*)$ para $Q(x)$ y evaluamos $g(x)$ ocurre que:
    \begin{align*}
    \frac{Q(x)-Q(a)}{g(x)-g(a)}&=\frac{0-Q(a)}{0-g(a)}\\
    &=\frac{Q(a)}{g(a)}
    \end{align*}
    Finalmente tenemos que:
    $$\frac{Q(a)}{g(a)}=\frac{f^{(n+1)}(t)}{(n+1)!} \Leftrightarrow Q(a)=\frac{f^{(n+1)}(t)}{(n+1)!}(x-a)^{n+1}.$$
    Ya que $Q(a)=R_{n,a}(x)$ concluimos:
    $$R_{n,a}(x)=\frac{f^{(n+1)}(t)}{(n+1)!}(x-a)^{n+1}.$$

$\square$

Ahora que hemos terminado la demostración, para los ejercicios que veremos a continuación podremos utilizar la forma del residuo que más nos convenga.

Ejercicios

  1. Consideremos la función $f(x)=e^{x}$ en $a=0$. Estima el error de la aproximación del polinomio de Taylor de grado $2$ para $x=\frac{1}{2}$.

Solución:
Primero obtengamos el Residuo de $f$ utilizando la forma de Lagrange:
\begin{align*}
R_{2,0}\left(\frac{1}{2}\right)&=\frac{f^{(2+1)}(t)}{(2+1)!}\left(\frac{1}{2}-0\right)^{2+1}\\
&= \frac{f^{(3)}(t)}{3!}\left(\frac{1}{2}\right)^{3}\\
\end{align*}

Como la tercera derivada de $f(t)$ es $e^{t}$, sustituyendo nos queda:
\begin{align*}
&= \frac{e^{t}}{3!}\left(\frac{1}{2}\right)^{3}\\
&= \frac{e^{t}}{6}\left(\frac{1}{8}\right)\\
&= \frac{e^{t}}{48}
\end{align*}

Del Teorema que vimos, sabemos que $t\in \left(0,\frac{1}{2}\right)$ por lo que se cumple la desigualdad:
$$ \frac{e^{t}}{48}< \frac{\sqrt{e}}{48}.$$
Observemos además que el valor de $e^{t}$ se encuentra dentro del intervalo:
$$(e^{0},e^{\frac{1}{2}})=(1,\sqrt{e}).$$

Así concluimos que el Residuo está acotado por el valor:
$$ \frac{\sqrt{e^{t}}}{48} \approx 0.034$$
$$\therefore R_{2,0}<0.034$$

De este modo el polinomio de Taylor $T_{2,0}\left(\frac{1}{2}\right)$ de grado $2$ con centro en $0$ para el valor $x=\frac{1}{2}$ aproxima a $f\left(\frac{1}{2}\right)=\sqrt{e}$ con un error menor que $0.034$.

  1. Brinda una aproximación del valor $\sqrt[3]{e^{2}}$ con un error menor a $10^{-4}$.

Solución:
Para resolver este problema vamos a considerar lo siguiente:
\begin{align*}
f(x)&= e^{x} & a&=0 & x&=\frac{2}{3}
\end{align*}

Observamos que en este caso no sabemos cuál es el valor $n$ del grado del polinomio de Taylor, esta variable $n$ es justo la que queremos encontrar. Comenzamos escribiendo el Residuo de Taylor en la forma de Lagrange sustituyendo los valores que sí conocemos:
\begin{align*}
R_{n,0}\left(\frac{2}{3}\right) &=\frac{f^{(n+1)}(t)}{(n+1)!}\left(\frac{2}{3}-0\right)^{n+1}\\
&= \frac{e^{t}}{(n+1)!}\left(\frac{2}{3})^{n+1}\right)\tag{ por $f^{(n+1)}(t)= e^{t}$}\\
\end{align*}

Como $t\in\left(0,\frac{2}{3}\right)$ tenemos la desigualdad:
$$ \frac{e^{t}}{(n+1)!}\left(\frac{2}{3}\right)^{n+1} < \frac{e^{\frac{2}{3}}}{(n+1)!}\left(\frac{2}{3}\right)^{n+1}$$
Donde $ \frac{e^{\frac{2}{3}}}{(n+1)!}\left(\frac{2}{3}\right)^{n+1}$ cumple:
$$ \frac{e^{t}}{(n+1)!}\left(\frac{2}{3}\right)^{n+1} < \frac{e^{\frac{2}{3}}}{(n+1)!}\left(\frac{2}{3}\right)^{n+1} < \frac{e}{(n+1)!}$$
Además como $\frac{e}{(n+1)!}$ es menor que $\frac{3}{(n+1)!}$:
$$ \frac{e^{t}}{(n+1)!}\left(\frac{2}{3}\right)^{n+1} < \frac{e^{\frac{2}{3}}}{(n+1)!}\left(\frac{2}{3}\right)^{n+1} < \frac{e}{(n+1)!}< \frac{3}{(n+1)!} $$

Así por la transitividad de las desigualdades tenemos que el Residuo cumple:
$$R_{n,0}< \frac{3}{(n+1)!}.$$

Sin embargo nos piden que el error sea menor que $10^{-4}$, por lo que necesitamos estudiar la desigualdad:
$$ \frac{3}{(n+1)!} < \frac{1}{10^{4}}.$$

Si reescribimos la desigualdad anterior:
\begin{align*}
\frac{3}{(n+1)!} < \frac{1}{10^{4}} &\Leftrightarrow (3)(10^{4})< (n+1)!\\
&\Leftrightarrow 30 000 < (n+1)!
\end{align*}

Ahora debemos pensar en un valor $n+1 \in \mathbb{N}$ cuyo factorial cumpla con ser mayor que $30 000$, veamos una lista:

\begin{align*}
1!&=1\\
2!&=2\\
3!&= 6\\
4!&= 24\\
5!&=120\\
6!&=720\\
7!&=5040\\
8!&= 40320
\end{align*}

Vemos que si $n+1=8$ ya logramos cumplir con la desigualdad, por lo que cuando consideramos el grado del Polinomio de Taylor $n=7$ para el valor $x=\frac{2}{3}$ cumplimos con que el error es menor a $10^{-4}$.

En la sección de Tarea moral te dejaremos algunos ejercicios que ayudarán a practicar lo estudiado en esta entrada.

Más adelante

Por el momento hemos terminado de revisar los temas concernientes a los polinomios de Taylor para este curso. En Cálculo Diferencial e Integral II revisarás algunos otros resultados. Para la próxima entrada, veremos algunas aplicaciones del Cálculo en el ámbito de la Economía.

Tarea moral

  • Realiza el ejercicio $1$ utilizando la forma de Cauchy para el residuo.
  • Para la función:
    $$g(x)=x\log(1+x).$$
    • Obtén el polinomio de Taylor de grado $n$ con $a=0$.
    • Obtén el Residuo de Taylor utilizando la forma de Lagrange.
    • Da una cota para el error al querer aproximar $10 \log\left(\frac{11}{10}\right)$ al utilizar el polinomio de Taylor de grado $3$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Polinomios de Taylor (Parte 1)

Por Karen González Cárdenas

Deja un comentario

Introducción

Recordemos que una función polinómica $p$ es de la forma:
$$p(x)=a_0+ a_1 x+ \ldots +a_n x^{n}$$
donde vemos que es fácil calcular el valor de $p$ para cualquier valor de $x$. Desafortunadamente, esto no es así con funciones como:
\begin{align*}
f(x)&= \sin(x) & g(x)&= \log(x) & h(x)&=e^{x}
\end{align*}

En esta entrada estudiaremos algunos resultados que nos ayudarán a encontrar polinomios que sean buenas aproximaciones a funciones como $f$, $g$ y $h$.

Revisitando a los polinomios

Si tenemos un polinomio:
$$p(x)=a_0+ a_1 x+ \ldots +a_n x^{n}$$
vemos que los coeficientes $a_i$ los podemos reescribir en términos de $p(x)$ y de sus derivadas en cero:
$$a_0=p(0).$$
Observación: Consideramos a la «derivada cero de $p$» como la función original.
$$p'(x)=a_1+2a_2 x+\ldots +n a_n x^{n-1} \Rightarrow a_1=p'(0)$$
\begin{align*}
p^{‘ ‘}(x)=2a_2+ \ldots + n(n-1)a_nx^{n-2} &\Rightarrow 2a_2=p^{‘ ‘}(0)\\
&\Rightarrow a_2=\frac{p^{‘ ‘}(0)}{2}
\end{align*}

Si continuamos con este procedimiento vemos que para el k-ésimo coeficiente ocurre que:
$$p^{k}(x)=k! \cdot a_k \Rightarrow a_k=\frac{p^{(k)}(0)}{k!}$$

Observaciones:

  • Consideramos $0! =1$ y recordemos que k factorial se define como:
    $$k!= 1 \cdot 2 \cdot \ldots \cdot (k-1) \cdot k$$
    Así $6! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 =720$.
  • Usaremos $p^{(k)}(0)$ para referirnos a la k-ésima derivada del polinomio en cero. Por lo que:
    $$p^{(0)}(0)=p(0)$$
  • $a_k$ está bien definido cuando $k=0$

Usando un desarrollo similar ahora para un polinomio de la forma:
$$p(x)=a_0+ a_1 (x-a)+a_2 (x-a)^{2}+ \ldots +a_n (x-a)^{n}$$
donde estamos reemplazando las potencias de $x$ por potencias de $x-a$.

Vemos que sus coeficientes $a_i$ en términos de $p$ en $a$ serían:
$$a_0=p(0)$$
$$p^{(1)}(x)=a_1+2a_2(x-a)+\ldots + n a_n (x-a)^{n-1} \Rightarrow a_1= p^{(1)} (a)$$
\begin{align*}
p^{(2)}(x)=2a_2+ \ldots +(n-1)(n) a_n (x-a)^{n-2} &\Rightarrow 2a_2 = p^{(2)}(a)\\
&\Rightarrow a_2 = \frac{p^{(2)}(a)}{2}
\end{align*}
\begin{align*}
p^{(3)}(x)= 6 a_3+ \ldots + (n-2)(n-1)(n)a_n(x-a)^{n-3} &\Rightarrow 6a_3 = p^{(3)}(a)\\
&\Rightarrow a_3 =\frac{ p^{(3)}(a)}{6}
\end{align*}
$$\vdots$$
Concluimos que:
$$a_k=\frac{p^{(k)}(a)}{k!}$$

Generalizando aún más…

Para generalizar más el planteamiento anterior, tomemos ahora una función $f$ que tiene sus $n$ derivadas en $a$:
$$f^{(1)}(a), \ldots , f^{(n)}(a).$$

Tenemos que los coeficientes $a_i$ en términos de $f(a)$ están dados por:
$$a_k=\frac{f^{(k)}(a)}{k!}$$
con $0 \leq k \leq n$.

Así definimos:
$$T_{n,a}(x)= a_0+a_1(x-a)+ \ldots + a_n(x-a)^{n}$$
al polinomio de Taylor de grado $n$ de la función $f$ en $a$.
Por lo que:
$$T_{n,a}^{(k)}(a)=f^{(k)}(a)\quad , 0\leq k \leq n.$$

Definición de polinomio de Taylor

Definición (Polinomio de Taylor): Sea $f: (x_0,y_0) \rightarrow \r$, $a \in (x_0,y_0)$ con $f$ n-veces derivable en $a$. El polinomio de Taylor para $f$ con centro en $a$ de grado $n$ se define como:
$$T_{n,a}(x)=\sum_{j=0}^{n} \frac{f^{(j)}(a)}{j!}(x-a)^{j}$$
donde $f^{(0)}(a)=f(a)$.

¿Es una buena aproximación?

Ya que hemos definido al polinomio de Taylor para una función $f$, queremos saber si éste es una buena aproximación. Para ello veamos la demostración del siguiente teorema:

Teorema: Sea $f: (x_0,y_0) \rightarrow \r$, $a \in (x_0,y_0)$ tal que $f$ es de clase $C^{(n)}$ en $a \Rightarrow$ existe el polinomio de Taylor $T_{n,a}$ con:
$$a_k=\frac{f^{k}(a)}{k!} \quad , 0 \leq k \leq n$$
que cumple con que:
$$\lim_{x \to a} \frac{f(x)-T_{n,a}(x)}{(x-a)^{n}}=0$$

Demostración: Iniciemos sustituyendo por definición a $T_{n,a}(x)$
\begin{align*}
\frac{f(x)-T_{n,a}(x)}{(x-a)^{n}} &= \frac{f(x)- \sum_{j=0}^{n} \frac{f^{(j)}(a)}{j!}(x-a)^{j}}{(x-a)^{n}}\\
&= \frac{f(x)- \sum_{j=0}^{n-1} \frac{f^{(j)}(a)}{j!}(x-a)^{j}}{(x-a)^{n}} – \frac{\frac{f^{(n)}(a)}{n!}(x-a)^{n}}{(x-a)^{n}}\\
&= \frac{f(x)- \sum_{j=0}^{n-1} \frac{f^{(j)}(a)}{j!}(x-a)^{j}}{(x-a)^{n}} – \frac{f^{(n)}(a)}{n!}
\end{align*}

Para facilitar un poco la redacción consideremos a:
\begin{align*}
S(x)&=\sum_{j=0}^{n-1} \frac{f^{(j)}(a)}{j!}(x-a)^{j}\\
h(x)&= (x-a)^{n}
\end{align*}

Por lo que tenemos:
$$\frac{f(x)-S(x)}{h(x)}- \frac{f^{(n)}(a)}{n!} .$$

Probemos que el límite cuando $x$ tiende a $a$ es cero:
$$\lim_{x \to a} \frac{f(x)-S(x)}{h(x)}- \frac{f^{(n)}(a)}{n!} =0.$$

Que es equivalente a probar que:
$$\lim_{x \to a} \frac{f(x)-S(x)}{h(x)}=\frac{f^{(n)}(a)}{n!}.$$
Observemos que para $h$ se tiene en sus derivadas los siguiente:
\begin{align*}
h^{(0)}(x)&= (x-a)^{n} = \frac{n! (x-a)^{n-0}}{(n-0)!}\\
h^{(1)}(x)&= n (x-a)^{n-1} = \frac{n! (x-a)^{n-1}}{(n-1)!}\\
h^{(2)}(x)&= n (n-1)(x-a)^{n-2} = \frac{n! (x-a)^{n-2}}{(n-2)!}\\
\end{align*}
$$\vdots$$
$$h^{(k)}(x)=\frac{n! (x-a)^{n-k}}{(n-k)!}$$

Y para $S(x)$ vemos que sus derivadas en $a$ son:
\begin{align*}
S(x)&=a_0+a_1 (x-a)+a_2(x-a)^{2}+ \ldots + a_{n-1}(x-a)^{n-1}\\
&\Rightarrow S(a)=a_0\\
S^{(1)}(x)&= a_1+2 a_2 (x-a)+ \ldots +(n-1)a_{n-1}(x-a)^{n-2}\\
&\Rightarrow S^{(1)}(a)=a_1\\
S^{(2)}(x)&= 2a_2+ \ldots + (n-1)(n-2)a_{n-1} (x-a)^{n-3}\\
&\Rightarrow S^{(2)}(a)=2 a_3
\end{align*}
$$\vdots$$

Reescribiendo los $a_i$ obtenemos:
\begin{align*}
S^{(0)}(a)&= \frac{f^{(0)}(a)}{0!}=f^{(0)}(a)\\
S^{(1)}(a)&= \frac{f^{(1)}(a)}{1!}=f^{(1)}(a)\\
S^{(2)}(a)&= \frac{f^{(2)}(a)}{2!}(2)=f^{(2)}(a)\\
\end{align*}

$$\vdots$$

\begin{align*}
S^{(k)}(a)&= \frac{f^{(k)}(a)}{k!}(k!)=f^{(k)}(a)
\end{align*}

De este modo al considerar los límites:
\begin{align*}
\lim_{x \to a}(f(x)-S(x)) &= f(a)- S(a)=0\\
\lim_{x \to a}(f^{(1)}(x)-S^{(1)}(x)) &= f^{(1)}(a)- S^{(1)}(a)=0\\
\end{align*}
$$\vdots$$
\begin{align*}
\lim_{x \to a}(f^{(n-2)}(x)-S^{(n-2)}(x)) &=0\\
\end{align*}

Y los límites para $h$:
\begin{align*}
\lim_{x \to a}h(x)&= g(a)= (a-a)^{n}=0\\
\lim_{x \to a} h^{(1)}(x)&=g^{(1)}(a)= \frac{n! (a-a)^{n-1}}{(n-1)!}=0\\
\end{align*}
$$\vdots$$
\begin{align*}
\lim_{x \to a} h^{(n-2)}(x)&=g^{( n-2 )}(a)= 0\\
\end{align*}
Del análisis anterior notamos que podemos aplicar la Regla de L’Hôpital que nos decía que teniendo que: $$\lim_{x \to a^+} f(x) = 0 = \lim_{x \to a^+} g(x).$$

Si $\lim\limits_{x \to a^+} \frac{f'(x)}{g'(x)} = L \in \RR$, entonces $\lim\limits_{x \to a^+} \frac{f(x)}{g(x)} = L$.

Así al hacerlo $n-1$ veces en el siguiente límite se da la igualdad:
\begin{align*}
\lim_{x \to a}\frac{f(x)-S(x)}{(x-a)^{n}}&=\lim_{x \to a}\frac{f^{(n-1)}(x)-S^{(n-1)}(x)}{\frac{n!(x-a)^{n-n+1}}{(n-n+1)!}}\\
&=\lim_{x \to a}\frac{f^{(n-1)}(x)-S^{(n-1)}(x)}{\frac{n!(x-a)}{(1)!}}\\
&=\lim_{x \to a}\frac{f^{(n-1)}(x)-S^{(n-1)}(x)}{n! (x-a)}\\
\end{align*}

Recordemos que $S(x)$ es un polinomio de grado $n-1$ por lo que al haberlo derivado $n-1$ veces lo que obtenemos para $S^{(n-1)}(x)$ es una constante que resulta ser:
$$ S^{(n-1)}(x) = f^{(n-1)}(a).$$

Sustituyendo en el límite:
\begin{align*}
\lim_ {x \to a}\frac{f^{(n-1)}(x)-S^{(n-1)}(x)}{n! (x-a)} &= \lim_{x \to a}\frac{ f^{(n-1)}(x)- f^{(n-1)}(a)}{n! (x-a) }\\
&= \frac{1}{n!}\left(\lim_{x \to a}\frac{ f^{(n-1)}(x)- f^{(n-1)}(a)}{x-a} \right )
\end{align*}

De este modo el límite resultante es por definición la n-ésima derivada de $f$ en $a$, es decir:
$$ \lim_{x \to a}\frac{ f^{(n-1)}(x)- f^{(n-1)}(a)}{x-a} = f^{(n)}(a).$$

Consecuentemente:
$$\lim_{x \to a}\frac{f(x)-S(x)}{(x-a)^{n}}=\frac{ f^{(n)}(a)}{n!}.$$

$\square$

Con la demostración terminada podemos afirmar que los polinomios de Taylor son una buena aproximación, ahora veamos algunos ejemplos.

Ejemplo 1

Comencemos por obtener el polinomio de Taylor para la función exponencial en $a=0$:
$$f(x)=e^{x}.$$
Veamos que todas las derivadas son de la forma:
$$f^{(k)}(x)=e^{x}.$$
Por lo que la k-ésima derivada valuada en $a=0$:
$$f^{(k)}(a)=e^{0}=1.$$
Sustituyendo en la definición de polinomio de Taylor tenemos:
$$T_{n,a}(x)=\sum_{j=0}^{n} \frac{1}{j!}x^{j}$$
Comencemos por ver cuáles serían los polinomios de Taylor de grado $0$,$1$ y $2$:
\begin{align*}
T_{0,0}(x)&=\frac{1}{0!}\\
T_{1,0}(x)&= \frac{1}{0!} + \frac{1}{1!}(x-0)\\
T_{2,0}(x)&= \frac{1}{0!} + \frac{1}{1!}(x-0) + \frac{1}{2!}(x-0)^{2}\\
\end{align*}

Al graficar dichos polinomios notamos que entre mayor es el grado del polinomio, mejor es la aproximación a la función:

Ejemplo 2

Ahora obtendremos el polinomio de Taylor de grado $5$ con centro en $a=0$ para:
$$g(x)=\sin(x).$$

Por lo que tenemos, calculamos las primeras cinco derivadas de $g$ y las evaluamos en cero:
\begin{align*}
g(x)&=\sin(0)=0\\
g^{(1)}(x)&=\cos(0)=1\\
g^{(2)}(x)&=-\sin(0)=0\\
g^{(3)}(x)&=-\cos(0)= -1\\
g^{(4)}(x)&=\sin(0)=0\\
g^{(5)}(x)&=\cos(0)=1\\
\end{align*}

Aplicando la definición de Taylor tenemos que su polinomio sería:
\begin{align*}
T_{5,0}&=\frac{0}{0!}(x-0)^{0}+\frac{1}{1!}(x-0)^{1}+\frac{0}{2!}(x-0)^{2}+\frac{(-1)}{3!}(x-0)^{3}+\frac{0}{4!}(x-0)^{4}+\frac{1}{5!}(x-0)^{5}\\
&=x-\frac{1}{3!}x^{3}+\frac{1}{5!}x^{5}
\end{align*}

Al graficar este polinomio $T_{5,0}=x-\frac{1}{3!}x^{3}+\frac{1}{5!}x^{5}$ vemos lo siguiente:

Ya que hemos revisado algunos ejemplos, en la siguiente sección te dejamos una lista de funciones de las que se te pide encontrar sus respectivos polinomios de Taylor siguiendo un procedimiento análogo.

Más adelante

Ahora que vimos la definición formal de los polinomios de Taylor, que resultan ser una buena aproximación para cualquier función $f$ con las características ya especificadas y algunos ejemplos, en la siguiente entrada veremos un resultado relacionado con su residuo.

Tarea moral

Obtener el polinomio de Taylor para las siguientes funciones:

  • $f(x)= \tan(x)$ de grado $3$ con $a=0$.
  • $g(x)= \sin(x)$ de grado $4$ con $a=\frac{\pi}{6}$.
  • $h(x)= e^{e^{x}}$ de grado $3$ con $a=0$.
  • $k(x)= \log(x+1)$ de grado $4$ con $a=0$.
  • $j(x)= \cos(x)$ de grado $m$ con $a=\frac{\pi}{2}$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»