Introducción

Anteriormente, comenzamos esta serie de entradas de geometría platicando de algunas técnicas euclideanas o sintéticas que se pueden usar para resolver problemas en el plano. Después, tomamos herramientas de la geometría analítica, las cuales nos permiten poner problemas en términos de coordenadas y ecuaciones. Lo que haremos ahora es ver varios ejemplos del uso de vectores en geometría.

A diferencia de la geometría analítica, cuando hablamos de soluciones por vectores estamos hablando de aquellas que aprovechan la estructura de espacio vectorial en $\mathbb{R}^2$. En otras palabras, usamos argumentos en los cuales pensamos a los puntos del plano como vectores, los cuales tienen una dirección y una magnitud. Los vectores tienen operaciones de suma y de producto por un escalar. Además, tienen producto punto, norma y transformaciones dadas por matrices. Apenas tocaremos la superficie del tipo de teoría que se puede usar. Un buen curso de álgebra lineal te puede dar más herramientas para resolver problemas geométricos.

Interpretar puntos como vectores

Pongamos un origen $O$ en el plano. A cada punto $P$ le corresponden ciertas coordenadas dadas por parejas de reales $(x,y)$, que identificaremos con $P$. Al origen le corresponden las coordenadas $(0,0)$. Si tenemos otro punto $Q=(w,z)$, entonces su suma es el vector $P+Q=(x+w,y+z)$. Si tomamos un real $r$, el vector $rP$ es el vector de coordenadas $(rx,ry)$.

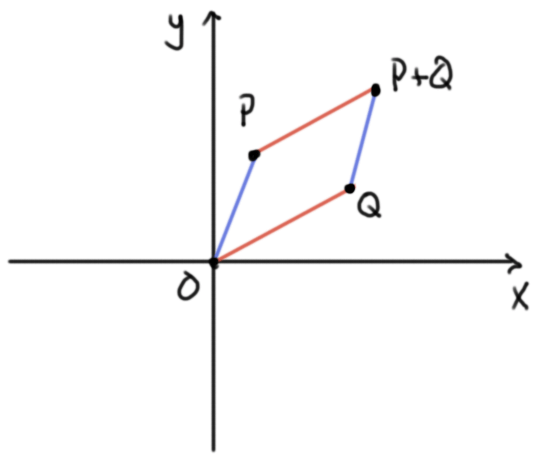
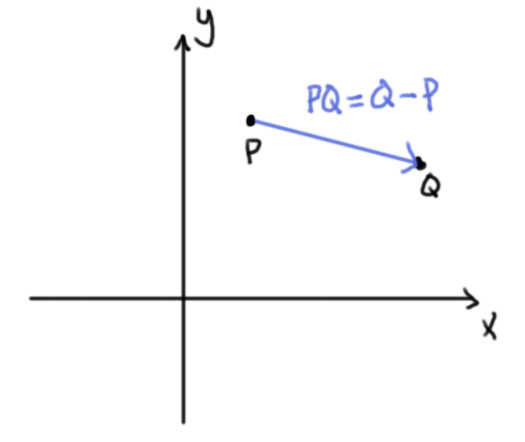
La suma $P+Q$ se puede encontrar mediante la ley del paralelogramo: los puntos $O,P,P+Q,Q$ hacen un paralelogramo en ese orden cíclico. La resta $Q-P$ está definida por $Q+(-1)P$, y la llamamos el vector $PQ$. Geométricamente coincide con el vector que va «de $P$ a $Q$». Observa que el orden es importante y que $OP=P$.

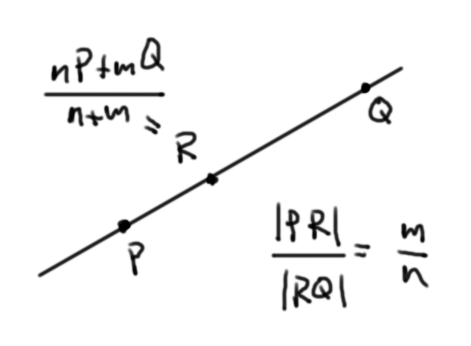
Proposición (de la razón). Si tenemos dos puntos $P$ y $Q$ distintos y $m,n$ son reales, entonces podemos encontrar al único punto $R$ en la recta por $P$ y $Q$ tal que $$\frac{PR}{RQ}=\frac{m}{n}$$ así: $$R=\frac{n}{m+n}P + \frac{m}{m+n} Q.$$

Veamos dos problemas en los que se usan estas ideas de vectores en geometría, en particular, la proposición de la razón.

Problema. En el triángulo $ABC$ se toman puntos $D,E,F$ sobre los segmentos $BC,CA,AB$ tales que $\frac{BD}{DC}=\frac{CE}{EA}=\frac{AF}{FB}=\frac{1}{4}$. Muestra que $ABC$ y $DEF$ tienen el mismo gravicentro.

Sugerencia pre-solución. Encuentra una fórmula en términos vectoriales para el gravicentro de un triángulo $ABC$.

Solución. Tomemos un triángulo $PQR$ y pensemos a sus vértices como vectores. Afirmamos que su gravicentro $X$ es el punto correspondiente a $\frac{P+Q+R}{3}$ Demostraremos esto.

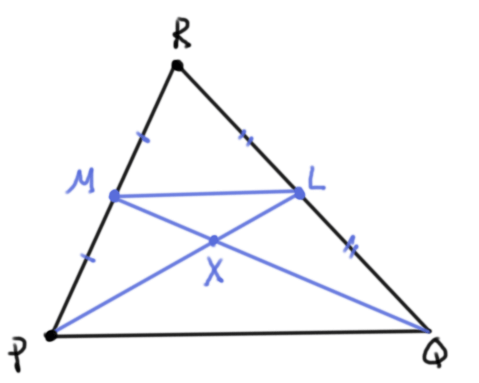
Primero haremos un argumento de geometría sintética. El gravicentro es por definición el punto de intersección de las medianas de un triángulo. Si $L$ es el punto medio de $QR$ y $M$ es el punto medio de $RP$, entonces $X$ es el punto de intersección de $PL$ y $QM$. Tenemos que $$\frac{RL}{LQ}=1=\frac{RM}{MP},$$ así que por el teorema de Tales se tiene que la recta por $L$ y $M$ es paralela al lado $PQ$, y $\frac{LM}{PQ}=\frac{1}{2}$. Esto muestra que los triángulos $XLM$ y $XPQ$ son semejantes en razón $1$ a $2$. Por lo tanto, $\frac{LX}{XP}=\frac{1}{2}$.

Ahora hagamos el argumento vectorial, pensando a los puntos como vectores. El punto $L$ está a la mitad de $QR$, así que por la proposición de la razón, $$L=\frac{Q+R}{2}.$$ El punto $X$ cumple $\frac{LX}{XP}=\frac{1}{2}$, así que de nuevo por la proposición de la razón.
\begin{align*}
X&=\frac{2L+P}{2+1}\\
&=\frac{Q+R+P}{3}\\
&=\frac{P+Q+R}{3}.
\end{align*}

Esto es el resultado auxiliar que queríamos mostrar. Regresemos al problema.

De acuerdo al resultado auxiliar, el gravicentro de $ABC$ es $$G:=\frac{A+B+C}{3}.$$ Usando una vez más la proposición de la razón, los puntos $D$, $E$ y $F$ los podemos calcular como sigue:
\begin{align*}
D&=\frac{4B+C}{4+1}=\frac{4B+C}{5}\\
E&=\frac{4C+A}{4+1}=\frac{4C+A}{5}\\
F&=\frac{4A+B}{4+1}=\frac{4A+B}{5}.
\end{align*}

De esta forma, el gravicentro $G’$ de $DEF$ lo podemos encontrar como sigue:
\begin{align*}
G’&=\frac{D+E+F}{3}\\
&=\frac{\frac{4B+C}{5}+\frac{4C+A}{5}+\frac{4A+B}{5}}{3}\\
&=\frac{A+B+C}{3}\\
&=G.
\end{align*}

Esto termina la solución del problema.

$\square$

Problema. En el paralelogramo $ABCD$ el punto $F$ es el punto medio de $CD$. Muestra que el segmento $AF$ corta a la diagonal $BD$ en un punto $E$ tal que $\frac{DE}{DB}=\frac{1}{3}$.

Sugerencia pre-solución. Hay varias formas de hacer las cuentas en este problema, pero el uso de una notación adecuada te hará simplificar muchas operaciones.

Solución. Pensemos a los puntos de la figura como vectores. Coloquemos al punto $A$ en el origen. El punto $C$ está dado por $B+D$, de modo que $$F:=\frac{C+D}{2}=\frac{B+2D}{2}.$$

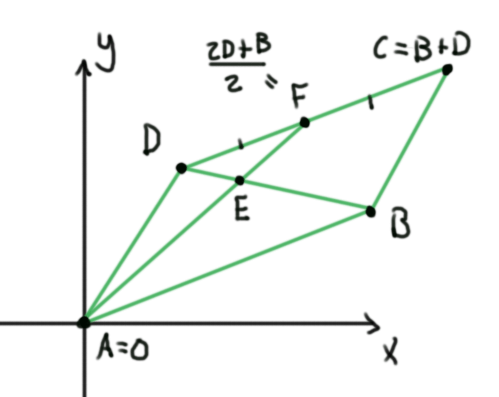
Para encontrar al punto $E$, notemos que está en las rectas $AF$ y $BD$. De esta forma, deben existir reales $r$ y $s$ tales que $$E=rF$$ y $$E=sB+(1-s)D.$$ Expresando $F$ en términos de $B$ y $D$ en la primer ecuación, tenemos que $$E=\frac{rB+2rD}{2}=\frac{rB}{2}+rD.$$ De ambas expresiones para $E$, concluimos que
\begin{align*}
s=\frac{r}{2}\\
1-s=r.
\end{align*}

Este sistema de ecuaciones tiene solución $r=\frac{2}{3}$, $s=\frac{1}{3}$, y por lo tanto $E=\frac{B+2D}{3}$. De aquí se obtiene $\frac{DE}{EB}=\frac{1}{2}$, o bien $\frac{DE}{DB}=\frac{DE}{DE+EB}=\frac{1}{3}$, como queríamos mostrar.

$\square$

Producto punto, norma y ángulos

Para dos vectores $P=(x,y)$ y $Q=(w,z)$ definimos su producto punto como la cantidad $P\cdot Q = xw+yz$. El productos puntos es:

• Conmutativo: $P\cdot Q = Q\cdot P$
• Abre sumas: $P\cdot (Q+R)=P\cdot Q + P\cdot R$
• Saca escalares: $(rP)\cdot Q = r(P\cdot Q)$.

La norma de $P$ se define como $\norm{P}=\sqrt{P\cdot P}$, y coincide con la distancia de $P$ al origen. La norma de $PQ$ es entonces $\norm{PQ}=\sqrt{(Q-P)\cdot (Q-P)}$ y coincide con la distancia de $P$ a $Q$.

El ángulo entre dos vectores $PQ$ y $RS$ se define como el ángulo cuyo coseno es $$\frac{PQ \cdot RS}{\norm{PQ}\norm{RS}},$$ y coincide precisamente con el ángulo (orientado) geométrico entre las rectas $PQ$ y $RS$. De esta forma, las rectas $PQ$ y $RS$ son perpendiculares si y sólo si el producto punto $PQ\cdot RS$ es cero.

Problema. Sea $ABC$ un triángulo con sus vértices pensados como vectores. Sean $H$ y $O$ su ortocentro y circuncentro respectivamente. Supongamos que el circuncentro $O$ está en el origen. Muestra que $H=A+B+C$.

Sugerencia pre-solución. Trabaja hacia atrás. Define al punto $A+B+C$ y ve que las rectas que unen a los vértices con este punto en efecto son alturas. Para calcular los ángulos, usa el producto punto y sus propiedades.

Solución. Como el circuncentro equidista de $A$. $B$ y $C$, tenemos que $$\norm{A}=\norm{B}=\norm{C}.$$ Tomemos el punto $H’=A+B+C$.

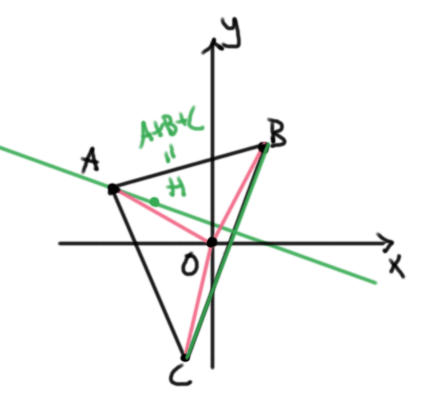
Calculemos el ángulo entre las rectas $BC$ y $AH’$, haciendo su producto punto:
\begin{align*}
BC\cdot AH’ &= (C-B)\cdot (H’-A)\\
&=(C-B)\cdot(C+B)\\
&=C\cdot C + C\cdot B – B\cdot C – B\cdot B\\
&=\norm{C}^2 – \norm{B}^2\\
&=0.
\end{align*}

Observa que estamos usando la linealidad y conmutatividad del producto punto. Al final usamos que $A$ y $C$ tienen la misma norma.

Esto muestra que la recta $AH’$ es la altura al lado $BC$. De manera análoga, $BH’$ y $CH’$ son las alturas a los lados $CA$ y $AB$ respectivamente. Por lo tanto, $H’$ es el ortocentro, así que $H=A+B+C$.

$\square$

Cualquier triángulo $ABC$ en el plano se puede trasladar para que su circuncentro $O$ quede en el origen. El ortocentro estará en $H=A+B+C$ y el gravicentro, como vimos antes, en $G=\frac{A+B+C}{3}$, que es un múltiplo escalar de $H$. Por lo tanto, $O$, $H$ y $G$ están alineados. Acabamos de demostrar con vectores en geometría un clásico resultado euclideano.

Teorema (recta de Euler). En cualquier triángulo $ABC$, el circuncentro $O$, el gravicentro $G$ y el ortocentro $H$ están alineados. Además, $$\frac{OG}{GH}=\frac{1}{2}.$$

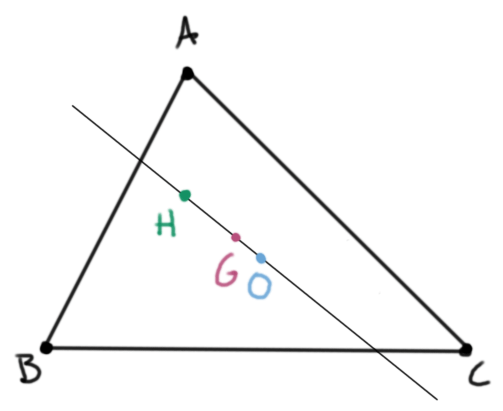
Si el circuncentro no está en el origen, ahora podemos usar el teorema de la recta de Euler y la proposición de la razón para concluir que $G=\frac{2O+H}{3}$. Usando que $G=\frac{A+B+C}{3}$, obtenemos el siguiente corolario

Corolario. Sea $ABC$ un triángulo en el plano, $H$ su ortocentro y $O$ su circuncentro. Entonces al pensar a los puntos como vectores tenemos que $$A+B+C=2O+H.$$

Más problemas

Puedes encontrar más problemas del uso de vectores en geometría en la sección 8.3 del libro Problem Solving through Problems de Loren Larson.