(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)
Introducción
En la entrada anterior definimos a los $p$-subgrupos de Sylow de un grupo $G$ como un $p$-subgrupo de $G$ tal que no estuviera contenido en otro $p$-subgrupo de $G$. En esta entrada estudiaremos los Teoremas de Sylow que hablan, como su nombre nos indica, de los $p$-subgrupos de Sylow que definimos antes.
El primero trata sobre del orden de los $p$-subgrupos de Sylow, que es la máxima potencia de $p$ que divide al orden del grupo $G$. El segundo habla de la relación entre los $p$-subgrupos de Sylow y establece que todo par de $p$-subgrupos son conjugados. El tercero describe de modo aproximado la cantidad de $p$-subgrupos de Sylow que hay en un grupo $G$, no nos da un número exacto, pero nos da alguna información al respecto.
Ahora, prepárate para leer el nombre de Sylow aún más veces.
Primer Teorema de Sylow
Teorema (Primer Teorema de Sylow). Sean $p\in\z^+$ un primo y $G$ un grupo finito con $|G|=p^t m$, $t\in\n^+, m\in \n^+, p\not{|}m.$ Entonces
- para cada $i\in\{1,\cdots,t\}$, $G$ contiene un subgrupo de orden $p^i$, y
- todo subgrupo de $G$ de orden $p^i$ con $i\in\{1,\cdots,t-1\}$ es un subgrupo normal de algún subgrupo de $G$ de orden $p^{i+1}$.
Demostración.
Sean $p\in\z^+$ un primo y $G$ un grupo finito con $|G|=p^tm$, $t,m\in \n^+$, $p\not{|}m$.
P.D. Para toda $i\in\{1,\cdots,t\}$ existe $P_i \leq G$ con $|P_i| = p^{i}$ y de forma que $P_i \unlhd P_{i+1}$ para toda $i\in\{1,\cdots,t-1\}$.
De hecho, con esto quedarían probados los dos incisos del PTS (Primer Teorema de Sylow).
Primero necesitamos un subgrupo de orden $p$. Éste se tiene gracias al Teorema de Cauchy. Así, podemos afirmar que $G$ tiene un subgrupo de orden $p$.
Ahora, si $i\in\{1,\cdots, t-1\}$ y $H$ es un subgrupo de orden $p^{i}$ veamos que podemos construir un subgrupo de $G$ de orden $p^{i+1}$ tal que $H$ sea normal a él:
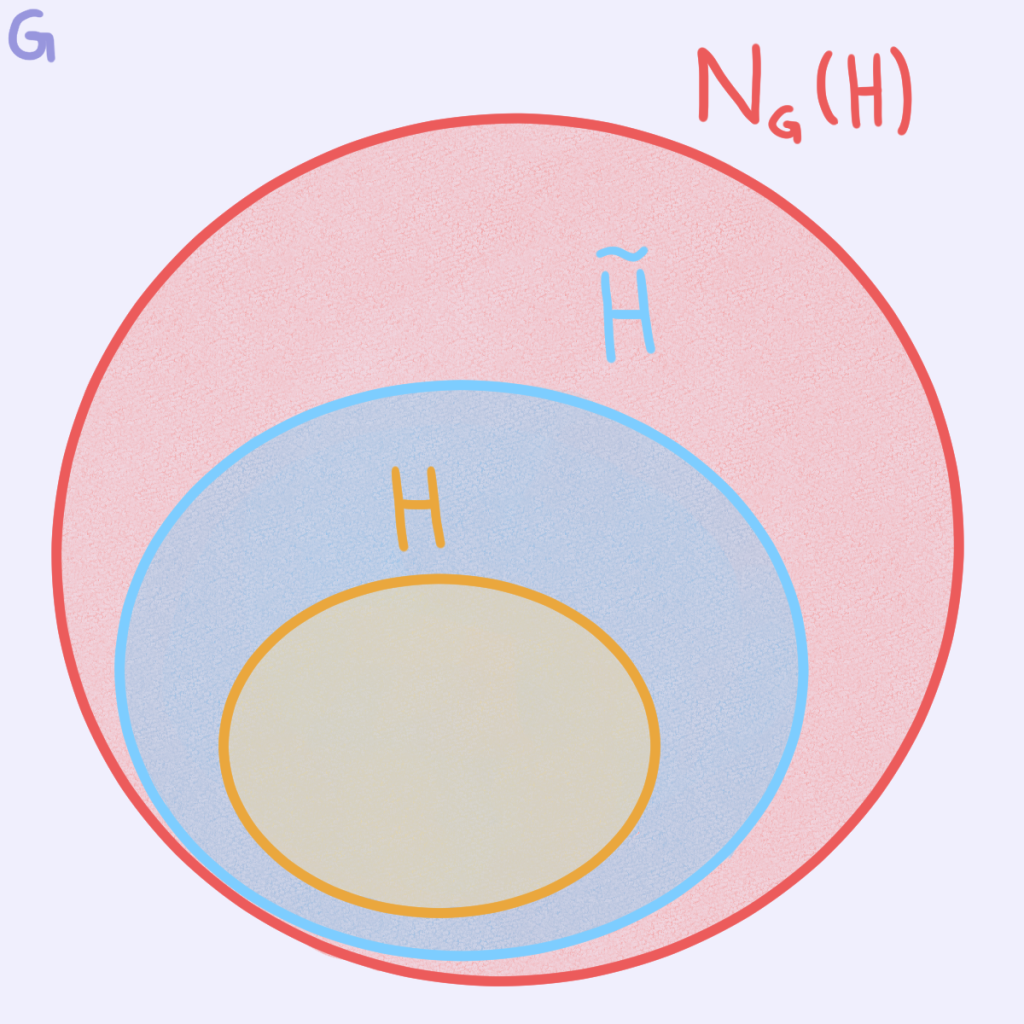
Sabemos que $p$ divide a $ [ G : H ]$ y como $[ G : H ] \equiv [ N_G(H) : H ] (\text{mód } p)$ entonces
\begin{align*}
p\text{ divide a } [ N_G(H) : H ] = \left| N_G(H) / H \right|.
\end{align*}
Entonces por Cauchy, el grupo cociente $N_G(H) / H$ tiene un subgrupo de orden $p$, y por el teorema de la correspondencia es de la forma $\tilde{H}/H$ con $H\leq \tilde{H} \leq N_G(H)$. Así,
\begin{align*}
&p = \left| \tilde{H} / H \right| = \frac{|\tilde{H}|}{|H|} = \frac{\tilde{H}}{p^{i}}
\\& \Rightarrow \frac{|\tilde{H}|}{p^{i}} = p
\\&\Rightarrow |\tilde{H}| = p^{i+1}
\end{align*}
pero $H\unlhd N_G(H)$ por construcción del normalizador y $ \tilde{H} \leq N_G(H)$, entonces $H \unlhd \tilde{H}.$
De esta manera, dado un subgrupo de orden $p^i$ podemos encontrar un subgrupo de orden $p^{i+1}$ tal que el primero sea normal en el segundo. Entonces, considerando $P_1$ un subgrupo de $G$ de orden $p$, existe $P_2$ un subgrupo de $G$ de orden $p^2$ tal que $P_1\unlhd P_2$ y a partir de $P_2$ podemos hallar $P_3$ un subgrupo de $G$ de orden $p^3$ tal que $P_2\unlhd P_3$ y así sucesivamente.
Concluimos entonces que existen $P_1,\cdots, P_t$ subgrupos de $G$ con $|P_i| = p^{i}$ para toda $i\in \{1,\cdots, t\}$ tales que $P_1 \unlhd P_2 \unlhd \cdots \unlhd P_t$.
$\blacksquare$
En consecuencia, el PTS nos dice qué tamaño tienen los $p$-subgrupos de Sylow, una incógnita que no habíamos resuelto. Esto se ilustra en el siguiente corolario.
Corolario. Sean $p\in\z^+$ un primo y $G$ un grupo finito con $|G| = p^tm$, $t,m,\in \n^+$ y $p\not{|}m$. Los $p$-subgrupos de Sylow de $G$ tienen orden $p^t$.
Segundo Teorema de Sylow
Antes de enunciar y probar el STS (Segundo Teorema de Sylow) vamos a hacer una observación.
Observación. Los conjugados de un $p$-subgrupo de Sylow son también $p$-subgrupos de Sylow.
Demostración.
Sean $p\in\z^+$ un primo y $G$ un grupo finito con $|G| = p^tm$ con $t,m\in\n^+$ y $p\not{|}m.$
Al tomar $P$ un $p$-subgrupo de Sylow de $G$, por el corolario del PTS sabemos que $|P| = p^t$.
Ahora, al conjugarlo mediante $g\in G$ se tiene que $gPg^{-1} \leq G$ con $|gPg^{-1}| = |P| = p^t$. Así, $gPg^{-1}$ es un $p$-grupo y debido a que su orden es la máxima potencia de $p$ que divide a $|G|$ se tiene que es un $p$-subgrupo de Sylow.
$\blacksquare$
Esta observación nos dice que todos los conjugados de un $p$-subgrupo de Sylow son igual a un $p$-subgrupo de Sylow, pero el STS va más allá y nos dice que conjugando $p$-subgrupos de Sylow podemos encontrar todos los $p$-subgrupos de Sylow de un grupo $G$.
Teorema (Segundo Teorema de Sylow). Sean $p\in \z^+$ un primo y $G$ un grupo finito. Todos los $p$-subgrupos de Sylow de $G$ son conjugados en $G$.
Demostración.
Sean $p\in \z^+$ un primo y $G$ un grupo finito, $P$ y $Q \; p$-subgrupos de Sylow de $G$.
Sea $X = \{gP \;|\; g\in G\}$. Para comenzar definimos $q\cdot(gP) = qgP$ para todas $q\in Q,g\in G.$ Ésta es una acción de $Q$ en $X$. Como $Q$ es un $p$-grupo, por el último teorema de la entrada Clase de Conjugación, Centro de $G$, Ecuación de Clase y $p$-Grupo sabemos que
\begin{align*}
\#X\equiv\#X_Q (\text{mód } p).
\end{align*}
Como $p$ no divide a $[ G: P ]$ y $[ G: P ] = \# X$, entonces $p$ tampoco divide a $\# X_Q$. En particular $\#X_Q \neq 0$ y así $X_Q \neq \emptyset$.
Pero
\begin{align*}
X_Q &= \{gP \;|\; q\cdot (gP) = gP \quad \forall q\in Q\}\\
&= \{gP \;|\; qgP = gP \quad \forall q\in Q\} \\
&= \{gP \;|\; g^{-1}qg \in P\quad \forall q\in Q\} \\
&= \{gP \;|\; g^{-1}Qg \subseteq P\} & \text{porque es para toda }q\in Q\\
&= \{gP \;|\; g^{-1}Qg = P\}.
\end{align*}
donde la última igualdad se da porque $g^{-1}Qg$ y $P$ son $p$-subgrupos de Sylow y entonces tienen el mismo orden, la máxima potencia de $p$ que divide al orden de $G$.
Así, $\{gP \;|\;g^{-1}Qg = P\}\neq \emptyset$ y en consecuencia existe $g\in G$ tal que $g^{-1}Qg = P$.
Por lo tanto $P$ y $Q$ son conjugados en $G$.
$\blacksquare$
Tercer Teorema de Sylow
Teorema (Tercer Teorema de Sylow). Sea $p\in \z^+$ un primo, $G$ un grupo finito y $r_p$ el número de $p$-subgrupos de Sylow de $G$. Entonces
- $r_p \equiv 1 (\text{mód } p)$,
- $r_p$ divide a $ |G|$.
Demostración.
Sean $p\in \z^+$ un primo, $G$ un grupo finito y $r_p$ el número de $p$-subgrupos de Sylow de $G$.
- Sea $X = \{P_1,\cdots, P_{r_p}\}$ la colección de todos los $p$-subgrupos de Sylow de $G$. Definimos $g\cdot P_i = gP_ig^{-1}$ para todas $g\in P_1$ e $i\in\{1,\cdots, r_p\}$, que es una acción de $P_1$ en $X$ ya que $ gP_ig^{-1}$ es nuevamente un $p$-subgrupo de Sylow por la observación previa. Como $P_1$ es un $p$-grupo, por el último teorema de la entrada Clase de Conjugación, Centro de $G$, Ecuación de Clase y $p$-Grupo sabemos que
\begin{align*}
\#X \equiv \# X_{P_1} (\text{mód } p).
\end{align*}
Pero por la construcción de $X$, tenemos que $$r_p = \#X\equiv \# X_{P_1} (\text{mód } p).$$
Ahora, veamos que $\#X_{P_1} = 1$ y para ello analicemos quién es $X_{P_1}$
\begin{align*}
X_{P_1} &= \{P_i \in X \;|\; g\cdot P_i = P_i \quad \forall g\in P_1\} \\
&= \{P_i \in X \;|\; gP_ig^{-1}=P_i \quad \forall g\in P_1\}.
\end{align*}
Así, para toda $P_i \in X_{P_1}$ se tiene que $P_1 \leq N_G(P_i)$ y también $P_i \leq N_G(P_i)$.
Entonces $P_1$ y $P_i$ son $p$-subgrupos de Sylow de $N_G(P_i).$
Por el Segundo Teorema de Sylow, $P_1$ y $P_i$ son conjugados en $N_G(P_i)$, es decir existe $g\in N_G(P_i)$ tal que
\begin{align*}
P_1 &= gP_ig^{-1} \\
&= P_i &\text{pues } g\in N_G(P_i).
\end{align*}
Concluimos entonces que $P_1$ es el único elemento en $X_{P_1}$ y así $\#X_{P_1} = 1$. Por lo tanto $r_p \equiv 1 (\text{mód } p)$. - Sea $X = \{P_1, \cdots, P_{r_p}\}$ la colección de todos los $p$-subgrupos de Sylow de $G$.
Definimos $g\cdot P_i = gP_ig^{-1}$ para todas $g\in G$ e $i\in\{1,\cdots, r_p\}$, que es una acción de $G$ en $X$.
Por el segundo teorema de Sylow sabemos que $P_1,\dots , P_{r_p}$ son conjugados de $P_1$, entonces $$ \mathcal{O}(P_1)=\{g\cdot P_1|g\in g\}=\{gP_1g^{-1}|g\in g\}=\{P_1,\dots , P_{r_p}\}=X$$ es decir, la acción es transitiva.
Entonces obtenemos que $r_p = \# \mathcal{O}(P_1)$. Pero, sabemos que $$\# \mathcal{O}(P_1) = [ G : G_{P_i} ] = \frac{|G|}{|G_{P_i}|}$$
que es un divisor de $|G|$. Por lo tanto $r_p$ es un divisor de $ |G|$.
$\blacksquare$
Tarea moral
- Demuestra el corolario del PTS: Sean $p\in\z^+$ un primo y $G$ un grupo finito con $|G| = p^tm$ donde $t,m,\in \n^+$ y $p\not{|}m$. Los $p$-subgrupos de Sylow de $G$ tienen orden $p^t$.
- Sean $p\in \z^+$ un número primo, $G$ un grupo y $P$ un $p$-subgrupo de Sylow de $G$. Demuestra que $P$ es el único $p$-subgrupo de Sylow de $G$ si y sólo si $P \unlhd G.$
- Sea $p\in \z^+$ un número primo. Da un ejemplo de un grupo finito $G$ que tenga tres $p$-subgrupos de Sylow $P$, $Q$ y $R$ tales que $P\cap Q = \{1\}$ y $P\cap R \neq \{1\}.$
(Sugerencia: Considera $S_3\times S_3.$) - Sean $p\in \z^+$ un número primo y $G$ un grupo finito. Considera $Q$ un $p$-subgrupo de $G$ tal que $Q \unlhd G$. Prueba que $Q \leq P$ para cada $p$-sugrupo de Sylow $P$ de $G$.
(Sugerencia: Usa el hecho de que cualquier otro $p$-subgrupo de Sylow de $G$ es conjugado de $P$.) - Sean $p\in \z^+$ un número primo y $G$ un grupo finito. Para cada primo $p$ divisor del orden de un grupo finito $G$, escoge un $p$-subgrupo de Sylow $Q_p$. Prueba que $$G = \left< \bigcup_p Q_p\right>.$$(Sugerencia: Usa el orden de los subgrupos generados por los subgrupos de Sylow.)
Más adelante…
En esta entrada abarcamos los tres Teoremas de Sylow, se colocaron los tres en esta entrada para que fuera más fácil consultarlos. Sin embargo, esto hace a la entrada un poco larga, así que la siguiente estará dedicada a algunos ejemplos de la aplicación de estos teoremas.
Entradas relacionadas
- Ir a Álgebra Moderna I.
- Entrada anterior del curso: $p$-Subgrupo de Sylow y el Normalizador de $H$ en $G$ .
- Siguiente entrada del curso: Ejemplos de Sylow.
- Resto de cursos: Cursos.