Introducción

Hasta ahora, hemos hablado de funciones integrables en un intervalo cerrado, en términos de ciertas sumas superiores e inferiores. Vimos en la entrada de Propiedades de la integral que si una función es monótona o continua, entonces su integral siempre está definida. Ahora veremos qué sucede con las funciones que tienen discontinuidades. En esta entrada trataremos a las funciones que finitas discontinuidades. En la siguiente hablaremos de funciones con una infinidad de discontinuidades.

Breve repaso de integrabilidad

Recordemos que para determinar si una función acotada $f:\mathbb{R}\to \mathbb{R}$ es integrable en cierto intervalo $[a,b]$, debemos calcular ciertas sumas superiores e inferiores con respecto a una partición. Esto es tomar algunos puntos $x_0<\dots <x_n$ en $[a,b]$, con $x_0=a$ y $x_n=b$. Escribimos $$P=\{x_0,x_1,\dots ,x_n\},$$

y decimos que $P$ genera los siguientes intervalos a los que llamamos celdas

$$[x_0,x_1],[x_1,x_2],\dots ,[x_{n-1},x_n].$$

A $[x_{k-1},x_k]$ le llamamos la $k$-ésima celda de $P$, cuya longitud es $\mathrm{\Delta }{x}_k=x_k-x_{k-1}$. Si $m_k$ es el ínfimo de los valores de $f$ en la $k$-ésima celda y $M_k$ es su supremo, entonces podemos definir respectivamente la suma inferior y superior como $$\underset{―}{S}(f,P)=\sum _{k=1}^n{m}_k\mathrm{\Delta }{x}_k\text{y}\bar{S}(f,P)=\sum _{k=1}^n{M}_k\mathrm{\Delta }{x}_k.$$

La función $f$ es integrable cuando el ínfimo de las sumas superiores (tomado sobre todas las particiones) coindice con el supremos de las sumas inferiores. Vimos que esto es equivalente a pedir que para todo $ϵ$ haya una partición en la que la suma superior y la inferior difieran menos que $ϵ$ (a lo que llamamos el criterio de Riemann). Probamos varias otras propiedades de esta definición, pero una que será muy importante para esta entrada es la siguiente.

Proposición. Sea $f:\mathbb{R}\to \mathbb{R}$ una función acotada. Sea $c$ cualquier valor entre $[a,b]$. Si la integral

$$\underset{a}{\overset{b}{\int }}f(x)dx$$

existe, entonces las dos integrales

$$\underset{a}{\overset{c}{\int }}f(x)dx,\underset{c}{\overset{b}{\int }}f(x)dx$$

también existen. Y viceversa, si estas dos integrales existen, entonces la primera también.

Cuando las tres integrales existen, se cumple además la siguiente igualdad:

$$\underset{a}{\overset{b}{\int }}f(x)dx=\underset{a}{\overset{c}{\int }}f(x)dx+\underset{c}{\overset{b}{\int }}f(x)dx.$$

Usaremos esta proposición en las siguientes secciones, pero necesitamos una versión un poco más versátil.

Proposición. Sea $f:\mathbb{R}\to \mathbb{R}$ una función acotada y $n$ un entero positivo. Sea $P=\{x_0,\dots ,x_n\}$ una partición de $[a,b]$. Si la integral $$\underset{a}{\overset{b}{\int }}f(x)dx$$ existe, entonces todas las integrales $${\int }_{x_{k-1}}^{x_k}f(x)dx$$ para $k=1,\dots ,n$ existen. Y viceversa, si estas $n$ integrales existen, entonces la primera también. Cuando todas estas integrales existen, entonces $$\underset{a}{\overset{b}{\int }}f(x)dx=\sum _{k=1}^n{\int }_{x_{k-1}}^{x_k}f(x)dx.$$

La demostración de esta proposición no es difícil, pues se sigue de la proposición anterior y de una prueba inductiva. Por ello, la encontrarás como parte de los ejercicios.

Funciones escalonadas

Hablaremos de la integrabilidad de funciones escalonadas, para lo cual necesitaremos la siguiente definición.

Definición. Una función $f:\mathbb{R}\to \mathbb{R}$ es escalonada en el intervalo $[a,b]$, si existe una partición $P=\{x_0,x_1,\dots ,x_n\}$ del intervalo $[a,b]$, tal que $f$ es constante en cada subintervalo abierto de $P$. Es decir, para cada $k=1,2,\dots ,n$ existe un número real $s_k$ tal que:

$$f(x)=s_k,\text{si}{x}_{k-1}<x<x_k.$$

A las funciones escalonadas también se les conoce como funciones constantes a trozos.

Ejemplo. En algunos sistemas postales se deben poner estampillas en una carta para poderse enviar. La cantidad de estampillas que hay que poner está determinada por el peso de la carta. Supongamos que una estampilla cuesta $5$ pesos y que hay que poner una estampilla por cada $20g$ (o fracción) que pese la carta, hasta un máximo de $100g$.

Si el peso de la carta en gramos está en el intervalo $[0,20]$, entonces tienes que pagar $5$ pesos. Si está en el intervalo $(20,40]$, pagarás 10 pesos y así sucesivamente hasta que llegue a 100 gramos. Gráficamente, el costo de envío tendría el siguiente comportamiento (puedes dar clic en la imagen para verla a mayor escala).

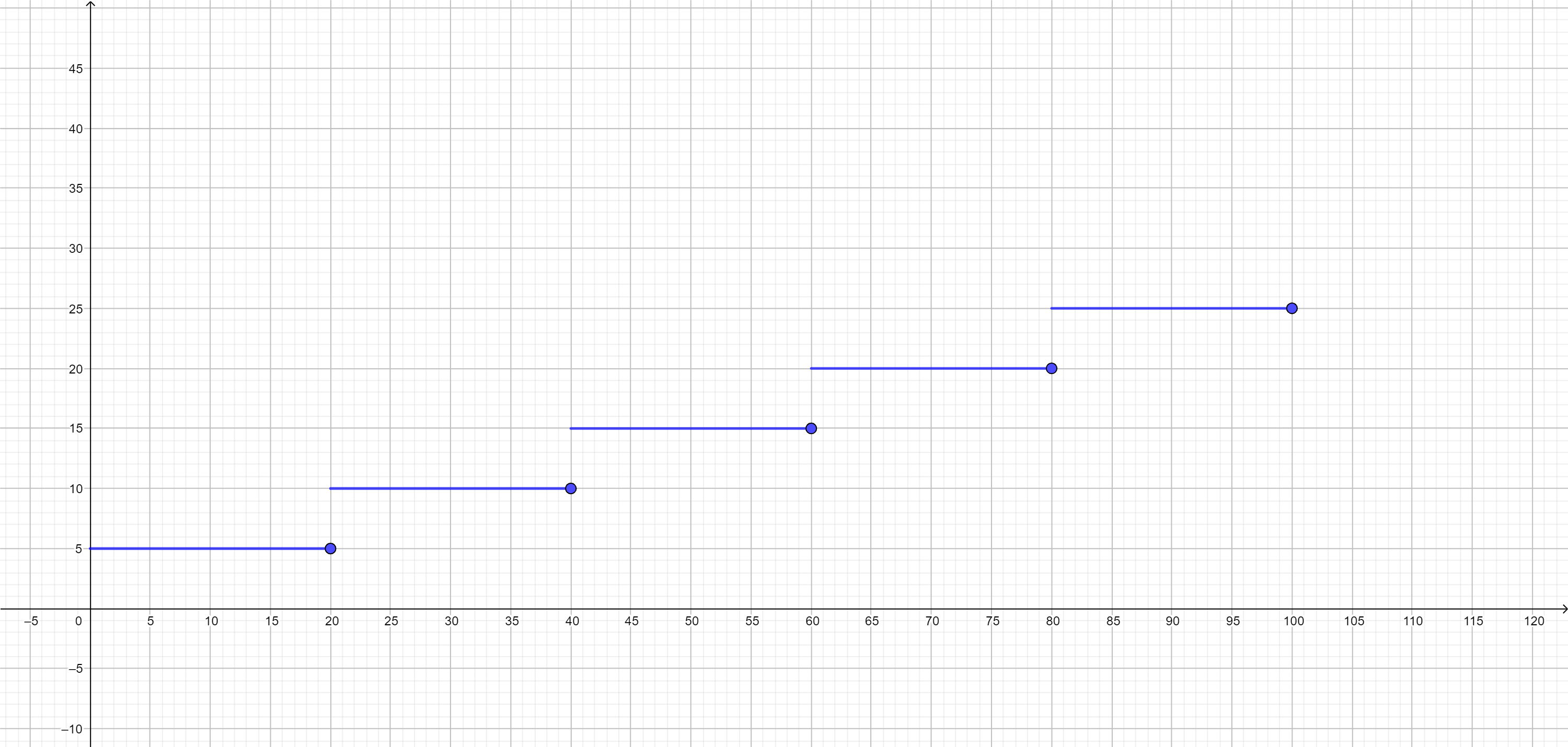
Observa que en efecto parece ser que hay «escalones». Esta función es escalonada pues al dar la partición $P=\{0,20,40,60,80,100\}$, tenemos que la función es constante en cada intervalo abierto definido por la partición.

Si quisiéramos calcular la integral de esta función, ¿qué podríamos hacer? Podemos utilizar la proposición de separar la integral en intervalos que enunciamos arriba, usando la misma partición $P$. Como la función es constante en cada intervalo dado, entonces su integral existe. Así, la integral en todo el intervalo $[0,100]$ existirá y será la suma de las integrales en cada intervalo. Tendrás que encontrar el valor exacto como uno de los ejercicios.

$\mathrm{△}$

Integral para funciones escalonadas

Las funciones escalonadas en un cierto intervalo siempre son integrables, como lo afirma el siguiente resultado.

Teorema. Sea $f:\mathbb{R}\to \mathbb{R}$ una función. Si $f$ es escalonada en un intervalo $[a,b]$, entonces es integrable en $[a,b]$. Además, si la partición que muestra que es escalonada es $P=\{x_0,\dots ,x_n\}$, y para $x$ en el intervalo $[x_{k-1},x_k]$ (para $k=1,\dots ,n$) se cumple que $f(x)=s_k$, entonces se tiene que $${\int }_a^{b}f(x)dx=\sum _{k=1}^n{s}_k(x_k-x_{k-1}).$$

El teorema nos dice entonces que el valor de la integral es la suma de los productos del valor $s_k$ (constante), por la longitud del $k$-ésimo intervalo. Esto tiene mucho sentido geométrico: cada uno de estos productos es el área de un rectángulo correspondiente a un «escalón». El teorema nos dice que el área buscada es la suma de las áreas de estos escalones.

Demostración. La demostración es consecuencia de la proposición para partir integrales en intervalos. Notemos que como $f$ es constante en cada intervalo $[x_{k-1},x_k]$ (para $k=1,\dots ,n$), entonces es integrable en dicho intervalo. En efecto, fijemos una $k\in \{1,\dots ,n\}$ y tomemos $Q=\{y_0,\dots ,y_m\}$ una partición de $[x_{k-1},x_k]$. En en este intervalo cualquier suma superior (o inferior) se hace tomando como supremo (o ínfimo) al valor constante $s_k$, de modo que:

$$\begin{array}{rl}\bar{S}(f,Q)& =\sum _{i=1}^m{M}_i\mathrm{\Delta }{y}_i\\ & =\sum _{i=1}^m{s}_k\mathrm{\Delta }{y}_i\\ & =s_k\sum _{i=1}^m\mathrm{\Delta }{y}_i\\ & =s_k(x_k-x_{k-1}),\\ \underset{―}{S}(f,Q)& =\sum _{i=1}^m{m}_i\mathrm{\Delta }{y}_i\\ & =\sum _{i=1}^m{s}_k\mathrm{\Delta }{y}_i\\ & =s_k\sum _{i=1}^m\mathrm{\Delta }{y}_i\\ & =s_k(x_k–x_{k-1}).\end{array}$$

Así, el ínfimo de las particiones superiores y el supremo de las inferiores es $c_k(x_k-x_{k-1})$, por lo que la integral existe en cada intervalo $[x_{k-1},x_k]$ y es igual a $c_k(x_k–x_{k-1})$. Usando la proposición que enunciamos en la sección de recordatorio sobre partir la integral por intervalos, obtenemos

$${\int }_a^{b}f(x)dx=\sum _{k=1}^n{\int }_{x_{k-1}}^{x_k}f(x)dx=\sum _{k=1}^n{s}_k(x_k-x_{k-1}),$$

como queríamos.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Funciones continuas a trozos

Las funciones escalonadas son muy sencillas, pero las ideas que hemos discutido respaldan una cierta intuición de que para la integrabilidad «si la función se comporta bien en cada uno de una cantidad finita de intervalos, entonces se comporta bien en todo el intervalo». Esa idea se repite a continuación.

Definición. Sea $f:\mathbb{R}\to \mathbb{R}$. Diremos que $f$ es continua a trozos en el intervalo $[a,b]$ si existe una partición $P=\{x_0,\dots ,x_n\}$ de $[a,b]$ tal que $f$ es continua en cada intervalo $(x_{k-1},x_k)$ para $k=1,\dots ,n$.

Pareciera que estamos pidiendo continuidad en todo el intervalo $[a,b]$. Sin embargo, hay algunas excepciones. Por la manera en la que está escrita la definición, la función $f$ no necesariamente es continua en los puntos $x_1,x_2,\dots ,x_{n-1}$.

Proposición. Sea $f:\mathbb{R}\to \mathbb{R}$ una función acotada. Si $f$ es continua a trozos en el intervalo $[a,b]$, entonces $f$ es integrable en $[a,b]$.

Demostración. Nos gustaría usar la proposición de separación de la integral por intervalos. Para ello, tomemos la partición $P=\{x_0,\dots ,x_n\}$ de $[a,b]$ tal que $f$ es continua en cada intervalo $(x_{k-1},x_k)$ para $k=1,\dots ,n$. Si $f$ fuera continua en cada intervalo cerrado $[x_{k-1},x_k]$, podríamos usar un resultado anterior para ver que es integrable en cada uno de estos intervalos, pero aquí tenemos una hipótesis un poco más débil, pues la continuidad es sólo en el abierto.

De cualquier manera, se puede ver que $f$ es integrable en cada intervalo cerrado $[x_{k-1},x_k]$. Para ello, fijemos $k$ y tomemos $ϵ>0$. Como $f$ es acotada, tiene supremo $M$ e ínfimo $m$ en $[a,b]$. Si $M=m$, entonces $f$ es constante y no hay nada que hacer. Así, supongamos $M\ne m$ y tomemos una $\delta >0$ tal que $2\delta (M-m)<\frac{ϵ}{2}$, y tal que $\delta <\frac{x_k-x_{k-1}}{2}$. La segunda condición nos dice que $[x_{k-1}+\delta ,x_k-\delta ]$ es no vacío. Como $f$ es continua en este intervalo cerrado, es integrable ahí. Por el criterio de Riemann, hay una partición $Q=\{y_1,\dots ,y_{l-1}\}$ de dicho intervalo tal que $$\bar{S}(f,Q)-\underset{―}{S}(f,Q)<\frac{ϵ}{2}.$$

Si a esta partición agregamos los puntos $y_0=x_{k-1}$ y $y_l=x_k$, entonces obtenemos una partición $Q^{\prime }=\{y_0,\dots ,y_l\}$ la cual su primera y última celda tienen longitud $\delta$ y cumple

$$\begin{array}{rl}\bar{S}(f,Q^{\prime })-\underset{―}{S}(f,Q^{\prime })& =(\bar{S}(f,Q)-\underset{―}{S}(f,Q))+(M_1-m_1)\mathrm{\Delta }{y}_1+(M_l-m_l)\mathrm{\Delta }{y}_l\\ & <\frac{ϵ}{2}+(M-m)\delta +(M-m)\delta \\ & =\frac{ϵ}{2}+2(M-m)\delta \\ & <\frac{ϵ}{2}+\frac{ϵ}{2}\\ & =ϵ.\end{array}$$

Así, hemos encontrado una partición $Q^{\prime }$ de $[x_{k-1},x_k]$ donde las sumas superior e inferior difieren en menos de $ϵ$. Por el criterio de Riemann, $f$ es integrable en ese intervalo, para cada $k=1,\dots ,n$. Concluimos la demostración usando nuevamente la proposición de separación de la integral en intervalos.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

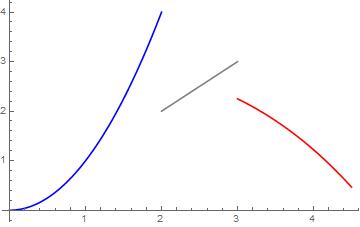
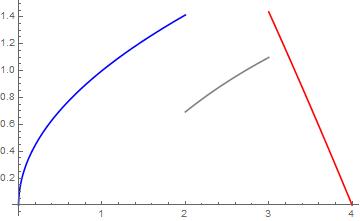
Ejemplo. La siguiente función $$f(x)=\{\begin{array}{lcc}{x}^2& si& 0\le x\le 2\\ \\ x& si& 2<x<3\\ \\ -\frac{x^3}{36}+3& si& 3\le x\le 4.5\end{array}$$

es integrable en el intervalo $[0,4.5]$. Tendrás que calcular su integral en los ejercicios.

$\mathrm{△}$

Funciones monótonas a trozos

Para esta discusión de funciones monótonas, vale la pena que tengas presente las definiciones de funciones crecientes y decrecientes, que puedes consultar en la entrada correspondiente del curso de Cálculo Diferencial e Integral I.

Definición. Una función $f:\mathbb{R}\to \mathbb{R}$ es monótona a trozos en el intervalo $[a,b]$ si existe una partición $P=\{x_0,\dots ,x_n\}$ de $[a,b]$ tal que $f$ es monótona en cada intervalo $(x_{k-1},x_k)$ para $k=1,\dots ,n$.

Podemos pensar cómo sería la gráfica de una función así. Tendría que estar formada por un número finito de trozos monótonos. Un ejemplo de ello son las funciones escalonadas (son por ejemplo, no crecientes a trozos). Un ejemplo un poco más interesante sería el de la siguiente figura.

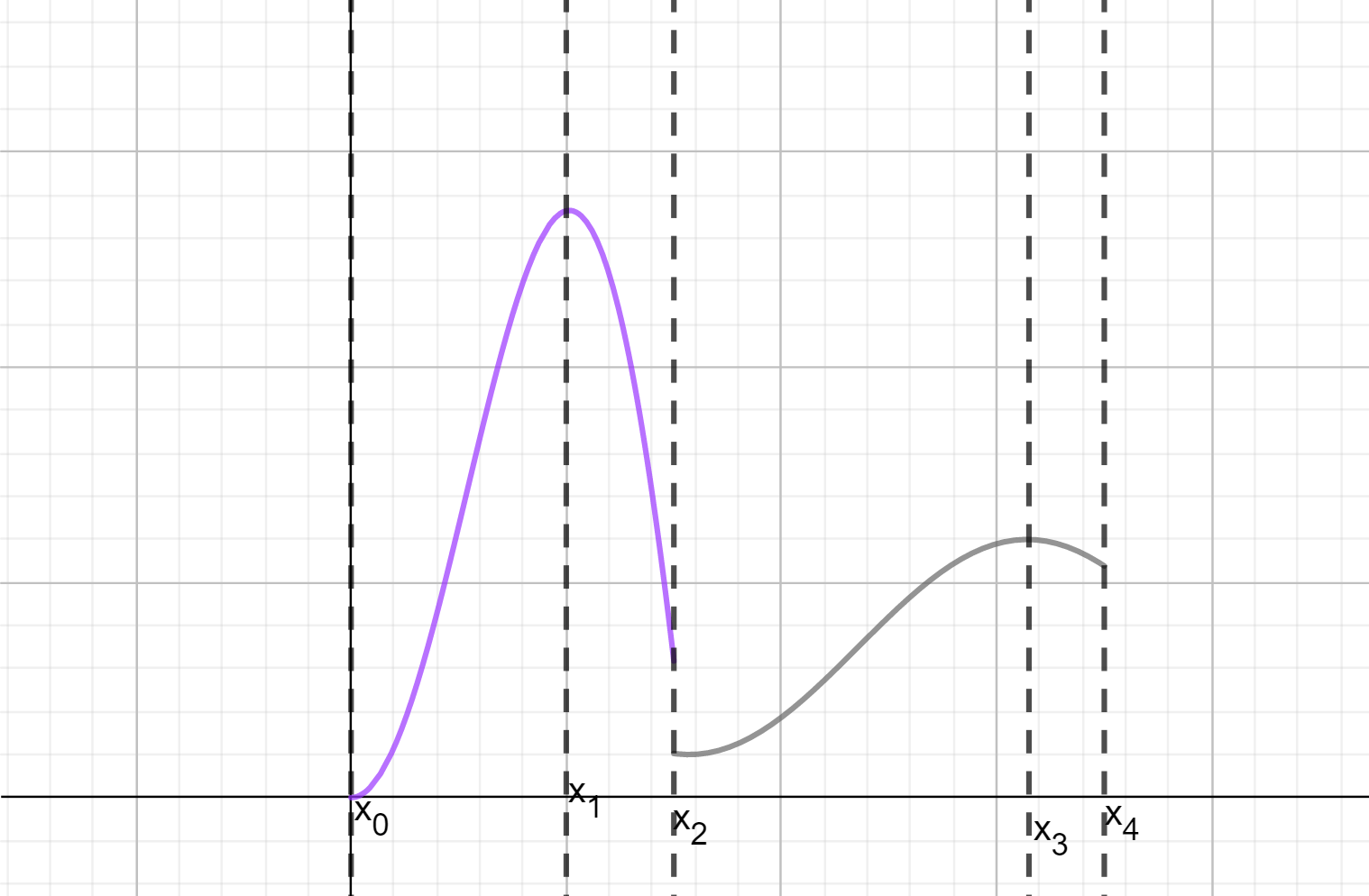
Como te imaginarás, las funciones monótonas a trozos también son integrables.

Proposición. Sea $f:\mathbb{R}\to \mathbb{R}$ una función acotada. Si $f$ es monótona a trozos en el intervalo $[a,b]$, entonces $f$ es integrable en $[a,b]$.

Una vez más, la demostración usa la proposición de separación de la integral por intervalos. Pero nuevamente nos enfrentamos con una dificultad. Lo que hemos demostrado anteriormente es que si una función es monónona en un intervalo $[x_{k-1},x_k]$, entonces es integrable en dicho intervalo. ¿Pero si sólo tenemos monotonía en $(x_{k-1},x_k)$? Para atender esta dificultad, se tiene que hacer una adaptación similar a lo que hicimos en la demostración para funciones continuas a trozos. Los detalles quedan como parte de la tarea moral.

Más adelante…

En esta entrada analizamos funciones con una cantidad finita de discontinuidades. También hablamos de las funciones monótonas a trozos, que podrían tener una infinidad de discontinuidades, pero también ser integrables. En la siguiente entrada veremos qué hacer con la integrabilidad cuando tenemos una cantidad infinita de discontinuidades.

Tarea moral

1. Calcula el valor de la integral de la función escalonada del servicio postal, con la partición dada.
2. Integra la siguiente función: $$f(x)=\{\begin{array}{lcc}{x}^2& si& 0\le x\le 2\\ \\ x& si& 2<x<3\\ \\ -\frac{x^3}{36}+3& si& 3\le x\le 4.5\end{array}$$

2. Integra la siguiente función. Puedes usar fórmulas de integración que conozcas de cursos preuniversitarios, sin embargo, toma en cuenta que tu respuesta será un poco informal hasta que mostremos de dónde salen dichas fórmulas. $$f(x)=\{\begin{array}{lcc}\sqrt{x}& si& 0\le x\le 2\\ \\ ln(x)& si& 2<x<3\\ \\ -\frac{x^2}{16}-x+5& si& 3\le x\le 4\end{array}$$

3. Demuestra por inducción la proposición de separación de la integral en intervalos que quedó pendiente en la sección de «Breve repaso de integrabilidad». Asegúrate de demostrar la ida y la vuelta.
4. Sean $f:\mathbb{R}\to \mathbb{R}$ y $g:\mathbb{R}\to \mathbb{R}$ funciones acotadas.
   • Muestra que si $f$ y $g$ son funciones escalonadas en un intervalo $[a,b]$, entonces $f+g$ y $fg$ también son funciones escalonadas en $[a,b]$. Sugerencia. Usa como partición un refinamiento común a las particiones $P$ y $Q$ que muestran que $f$ y $g$ son escalonadas, respectivamente.
   • Muestra que si $f$ y $g$ son funciones continuas por trozos en un intervalo $[a,b]$, entonces $f+g$ y $fg$ también son funciones continuas por trozos en $[a,b]$.
   • Si $f$ y $g$ son funciones monótonas por trozos en un intervalo $[a,b]$, ¿será que $f+g$ y $fg$ también lo son? ¿Bajo qué condiciones de la monotonía sí sucede esto?
5. Da un ejemplo de una función que sea monótona por trozos, pero que no sea continua por trozos.
6. Demuestra la proposición de que las funciones monónotas a trozos son integrables.

Entradas relacionadas

• Página del curso: Cálculo Diferencial e Integral II
• Entrada anterior: Teorema del valor medio para la integral
• Entrada siguiente: Funciones integrables con infinitas discontinuidades