Introducción
De la definición de Inversión se tiene la siguiente propiedad, se tienen $P$ y $P’$ dos puntos inversos respecto a la circunferencia $C(O,r)$, y cada uno de estos describe una curva, $P$ describe a $C$ y $P’$ describe a $C’$. Estas curvas son inversas una de la otra, se les llama mutuamente inversas.
Inversión de Rectas y Circunferencias
Se tienen 2 curvas $C$ y $C’$ inversas una de la otra, las cuales se intersecan, esto lo hacen sobre la circunferencia de Inversión, debido a que el punto en común debe ser su propio inverso, y el inverso de un punto en la $C(O,r)$ es el propio punto en la circunferencia de inversión.
Dado lo anterior se puede ver la inversión aplicada a 2 objetos geométricos: Rectas y Circunferencias.
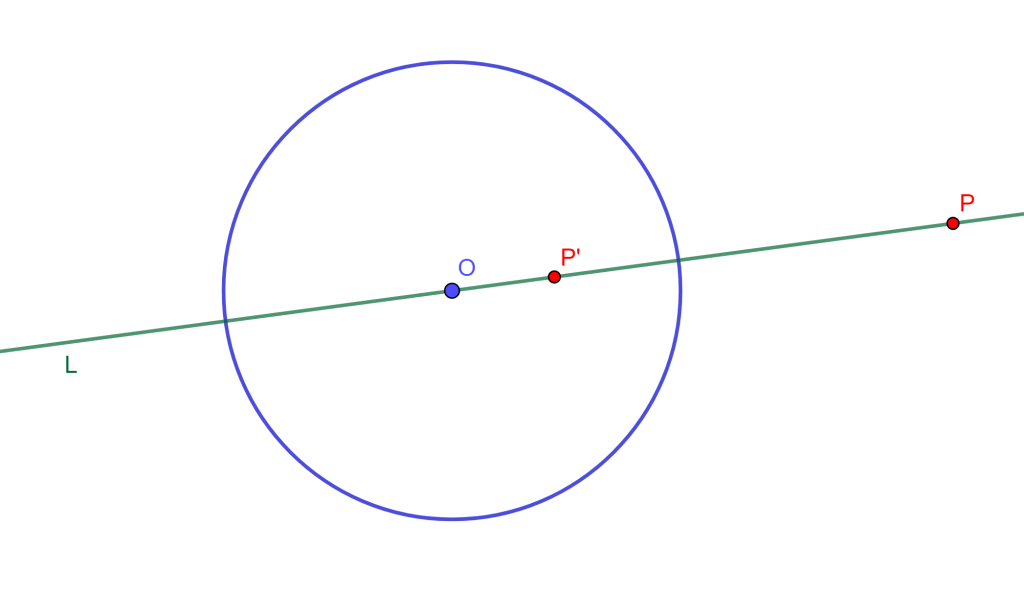
Teorema. Sea $C(O,r)$ una circunferencia de inversión y $L$ una recta que pasa por $O$, entonces el inverso de $L$ respecto a $C(O,r)$ es el mismo $L$.
Demostración. Tenemos una circunferencia $C(O,r)$ y $L$ una recta por $O$, además todo punto $P$ en $L$ tiene su inverso $P’$ tal que $O,P$ y $P’$ son colineales entonces $OP \times OP’ =r^2$.
Por lo cual los inversos de los puntos de $L$, también están en la misma recta $L$.
Por lo tanto, $L$ su inverso es el mismo $L$.
$\square$
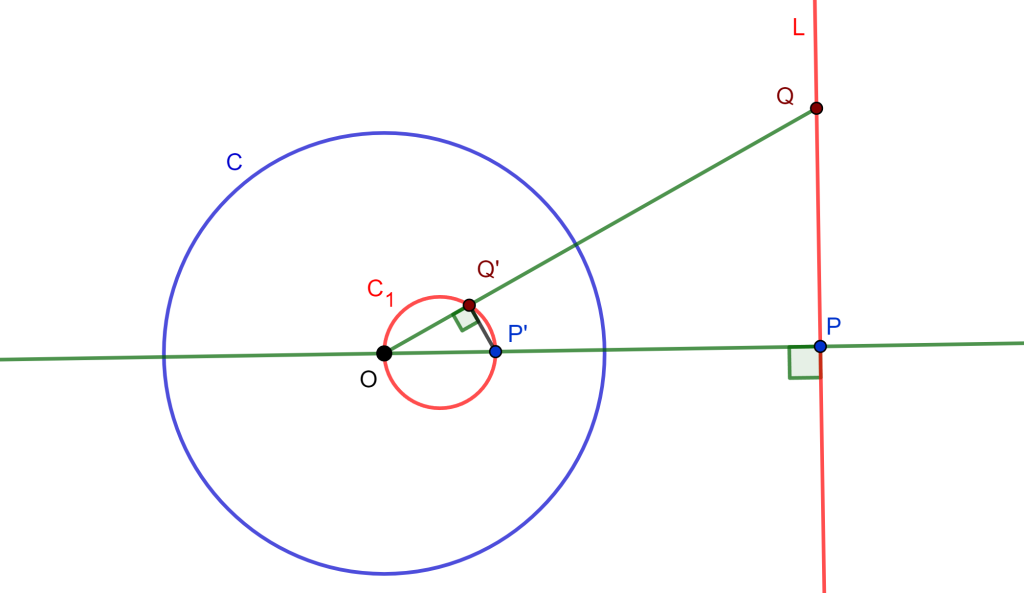
Teorema. Sea $C(O,r)$ una circunferencia de inversión y $L$ una recta que no pasa por $O$, entonces el inverso de $L$ respecto a $C$ es una circunferencia que pasa por $O$. Recíprocamente, el inverso de una circunferencia que pasa por el centro de inversión es una recta que no pasa por el centro de inversión.
Demostración. Sea $P$ el pie de la perpendicular desde $O$ a $L$ y sea $Q \neq P$, donde $Q \in L$ y de estos obtenemos $P’$ y $Q’$ los inversos respecto a $C$ de $P$ y $Q$ respectivamente.
$\Rightarrow OP \times OP’ =r^2$ y $OQ \times OQ’=r^2$
$\Rightarrow OP \times OP’ = OQ \times OQ’$
$\Rightarrow \frac{OP}{OQ’} = \frac{OQ}{OP’}$
$\Rightarrow \triangle OQ’P’ \approx \triangle OPQ$
Esto ya que comparten 2 lados proporcionales y un ángulo en común $\angle O$.
Ahora $\triangle OPQ$ es rectángulo, entonces $\triangle OQ’P’$ es rectángulo, por lo cual $OP’$ es un diámetro de una circunferencia que pasa por $Q’$.
Análogamente, si tuviéramos un $R \in L$, $R \neq P$ y $R \neq Q$, su inverso $R’$ cumplirá $\frac{OP}{OR’} = \frac{OR}{OP’}$, con lo que $\triangle OPR \approx \triangle OR’P’$, por lo cual $\triangle OR’P’ $ es rectángulo, como $OP’$ es fijo se sigue que la circunferencia del diámetro $OP’$ que pasa por $Q’$ también pasa por $R’$.
Por lo tanto, el inverso de $L$ respecto a $C$ es $C_1$ una circunferencia que pasa por $O$.
$\square$
Inversamente, si $Q’$ es un punto de $C_1$ circunferencia, recorriendo al revés los pasos de la demostración anterior, que $Q$ está en la perpendicular a la línea del diámetro $OP’$ que pasa por el inverso de $P’$.
$\square$
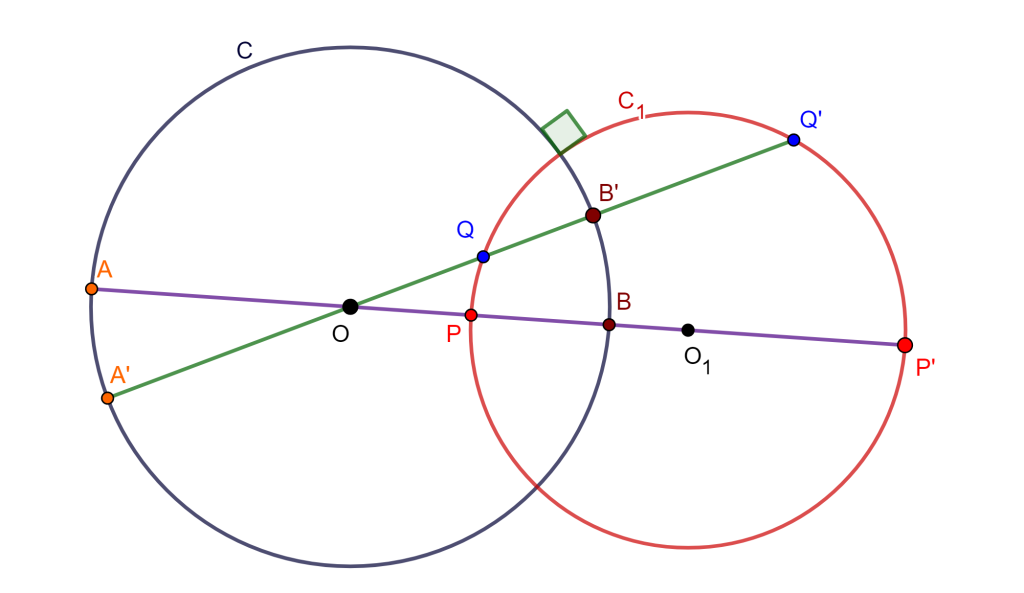
Teorema. Sea $C(O,r)$ una circunferencia de inversión y sea $C_1$ una circunferencia ortogonal a $C$, el inverso de $C_1$ es $C_1$.
Demostración. Se traza una recta que pase por $O$ y $O_1$, la cual nos genere intersecciones en $C$ las cuales son $A$ y $B$, de igual forma en $C_1$ se genera $P$ y $P’$.
Sea $C \perp C_1$ ortogonal, entonces $P$ y $P’$ son armónicos respecto a $A$ y $B$.
$\Leftrightarrow \frac{AP}{PB} = \frac{-AP’}{P’B} $
$\Leftrightarrow OP \times OP’ =r^2$
$\Leftrightarrow P$ y $P’$ son inversos respecto a $C$.
Tracemos una recta que pase por $O$ y corte a $C_1$ en $Q$ y $Q’ \in C_1$, y a $C$ en $A’$ y $B’ \in C$, tales que $Q$ y $Q’$ son armónicos respecto a $A’$ y $B’$
$\Leftrightarrow \frac{A’Q}{QB’} = \frac{-A’Q’}{Q’B’} $
$\Leftrightarrow OQ \times OQ’ =r^2$
$\Leftrightarrow P$ y $P’$ son inversos respecto a $C$.
Todo punto en una circunferencia ortogonal a la de inversión tiene su inverso en ella misma. Por lo tanto, $C_1$ es su propia inversa.
$\square$
Tenemos observaciones que nos indica que los siguientes son sus propios inversos con respecto a la circunferencia de Inversión:
- La propia circunferencia de Inversión
- Rectas por el centro de Inversión
- Circunferencias ortogonales a la circunferencia de Inversión
Teorema. El inverso de una circunferencia que no pasa por el centro de inversión, es otra circunferencia que tampoco pasa por el centro de Inversión.
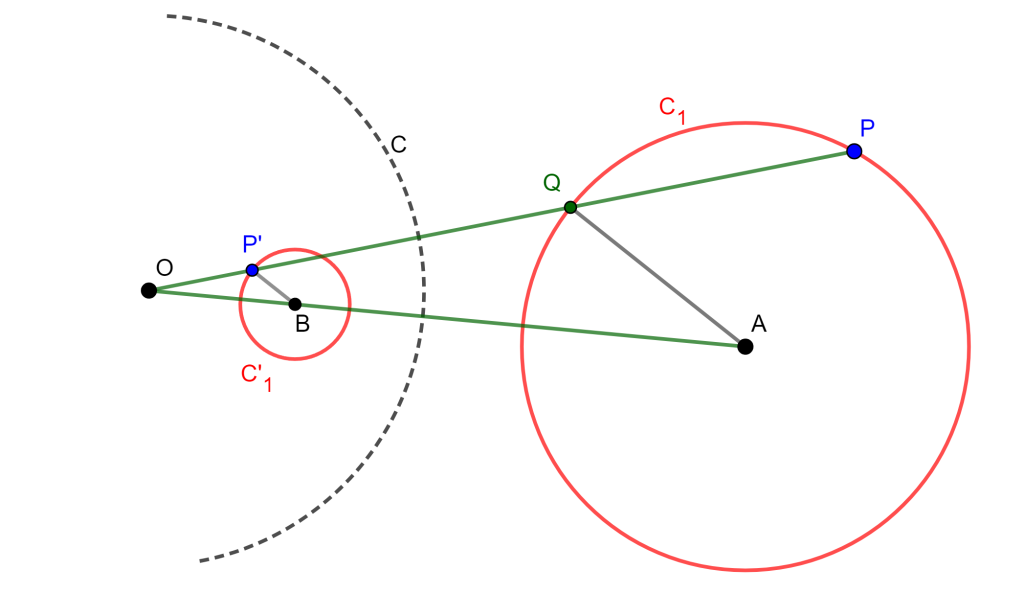
Demostración. Tenemos $C_1$ una circunferencia con centro $A$, tomemos un punto $P$ sobre la circunferencia $C_1$, también tenemos $C(O,r)$ una circunferencia con centro de Inversión $O$.
Tracemos una recta $OP$, genera un punto de intersección $Q$, y se genera $P’$ inverso de $P$. Ahora tracemos la recta $OA$ y $QA$, además tracemos una paralela a $QA$ que interseque a $OA$ en $B$
Por definición de Inversión $OP \times OP’=r^2$ y $OQ \times OP = w$, ahora como los triángulos $\triangle OBP’$ y $\triangle OAQ$ son semejantes, entonces
$\Leftrightarrow \frac{OP’}{OQ} = \frac{OB}{OA}=\frac{BP’}{AQ} $
$\Leftrightarrow \frac{OP’}{OQ} = \frac{OB}{OA} $
$\Leftrightarrow OB=\frac{OP’ \times OA}{OQ} $ como $OQ = w/OP$
$\Leftrightarrow OB=\frac{OP’ \times OA}{w/OP} =\frac{OP’ \times OP\times OA}{w}=\frac{r^2 \times OA}{w} $
Entonces $OB$ es constante, $B$ es un punto fijo y $BP’$ es finita y constante, entonces el lugar geometrico de $P’$ es una circunferencia $C’_1$, por lo cual el punto $P’$ no pasa por $O$.
Por lo tanto, el Inverso de $C_1$ es $C’_1$.
$\square$
Observación. Note que $P$ y $P’$ son puntos antihomologos, $Q$ y $P’$ son homólogos y $O$ es el centro de homotecia de las circunferencias $C_1$ con centro $A$ y $C’_1$ con centro $B$.
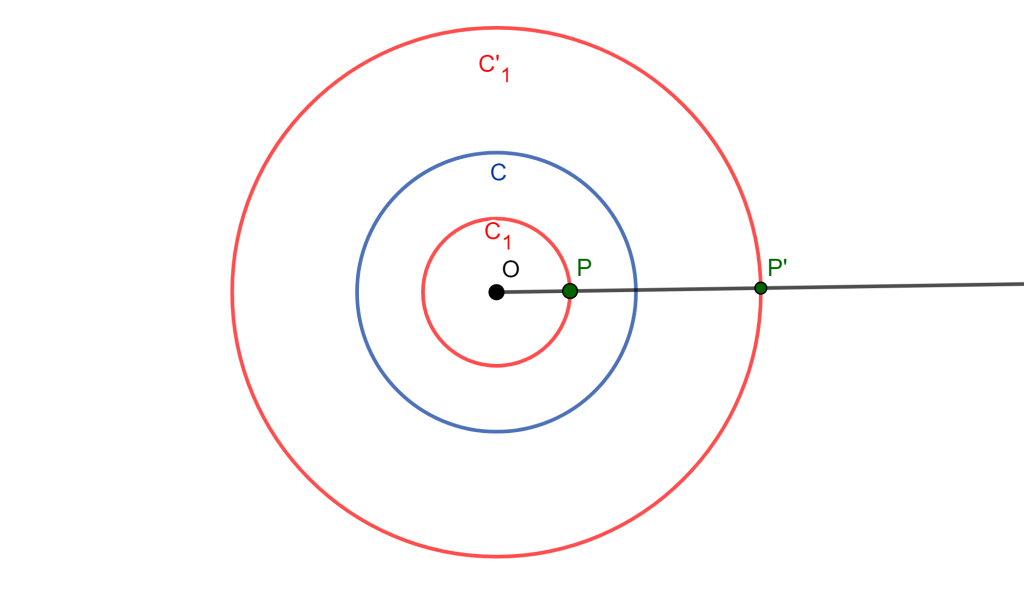
Teorema. El inverso de una circunferencia concéntrica con la circunferencia de inversión, es otra circunferencia concéntrica con la circunferencia de inversión.
Demostración. Sea $C(O,r)$ nuestra circunferencia de Inversión y $C_1$ una circunferencia concéntrica a $C$
Tomemos un punto en $C_1$ el cual es $P$, del cual su inverso es $P’$ con respecto a $C(O,r)$, entonces la distancia $OP$ es constante, al igual $r$ es constante y por definición de inversión $OP \times OP’ =r^2$ entonces $OP’=r^2/OP$ por lo cual $OP’$ es constante.
Por lo tanto, el inverso de $C_1$ es una circunferencia $C’_1$ con centro $O$ y radio $OP’$.
$\square$
Más adelante…
Otro aspecto a analizar de la inversión será la conservación de ángulos.
Entradas relacionadas
- Ir a Geometría Moderna II
- Entrada anterior del curso: Puntos Inversos con respecto a una circunferencia
- Siguiente entrada del curso: Conservación de ángulos