2.3 Conservación de ángulos y razón cruzada

Introducción

Ya analizado en el anterior tema, la inversión de rectas y circunferencias, es momento de ver como la inversión hace conservación de ángulos.

Teorema (Conservación de ángulos)

La inversión es una transformación, que preserva ángulos e invierte orientación.

Demostración

Para ello lo demostraré de dos maneras distintas:

1.º Forma

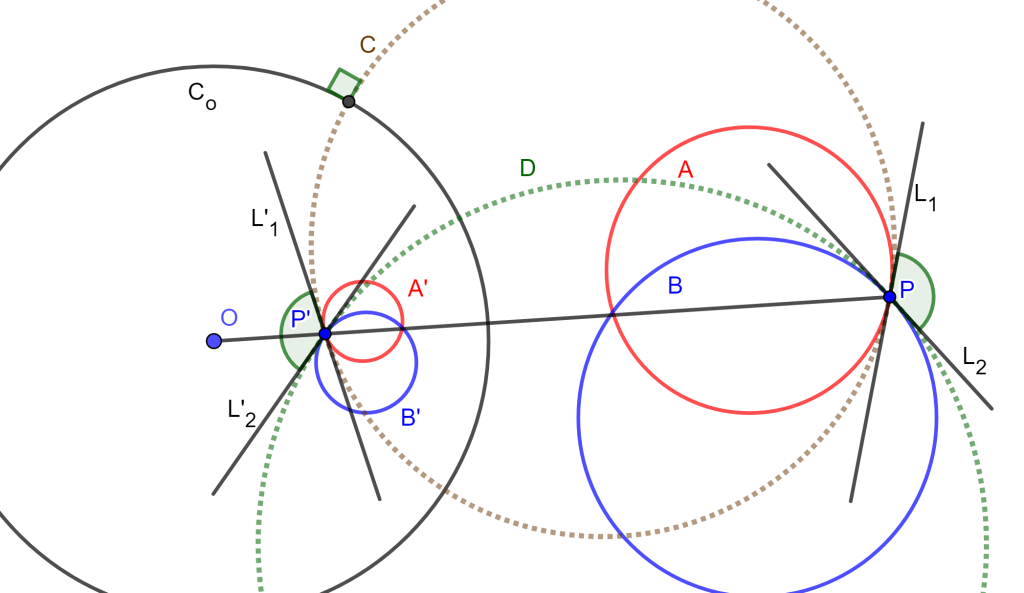
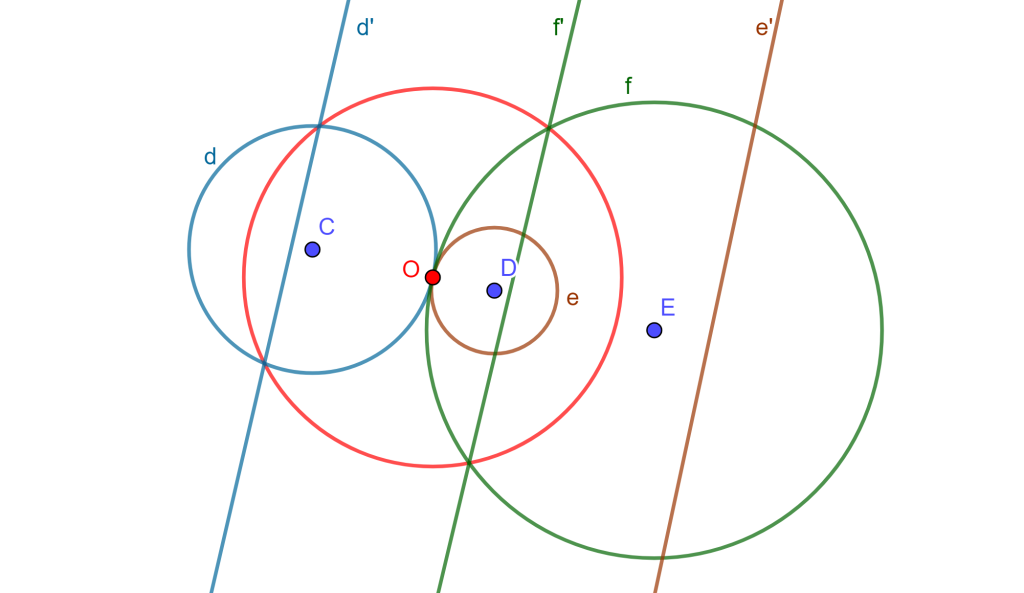
Se tiene una circunferencia de inversión $C_o(O,r)$, $A$ y $B$ circunferencias que se intersecan, y sea $P$ uno de los puntos de intersección, además se tiene $P’$ inversa de $P$.
Ahora construyamos la circunferencia $C$ tangente a $A$ en $P$ y que pase por $P’$, de igual forma se construye $D$ tangente a $B$ en $P$ y que pase por $P’$. Sea $L_1$ recta tangente a $A$ en $P$ y de igual forma tangente a $C$ en $P$, sea $L_2$ recta tangente a $B$ en $P$ y es tangente a $D$ en $P$, entonces el ángulo entre $A$ y $B$ es el mismo entre $C$ y $D$.
Como $C$ y $D$ pasan por puntos inversos, entonces son ortogonales a $C_o$ la circunferencia de inversión, $P$ y $P’$ son ortogonales entre $A’$ y $B’$ dos circunferencias inversas a $A$ y $B$ respectivamente, entonces se tiene que el ángulo entre $A’$ y $B’$ es el mismo entre $A$ y $B$.
Por lo tanto, la inversión preserva ángulos e invierte orientación $_\blacksquare$

2.º Forma

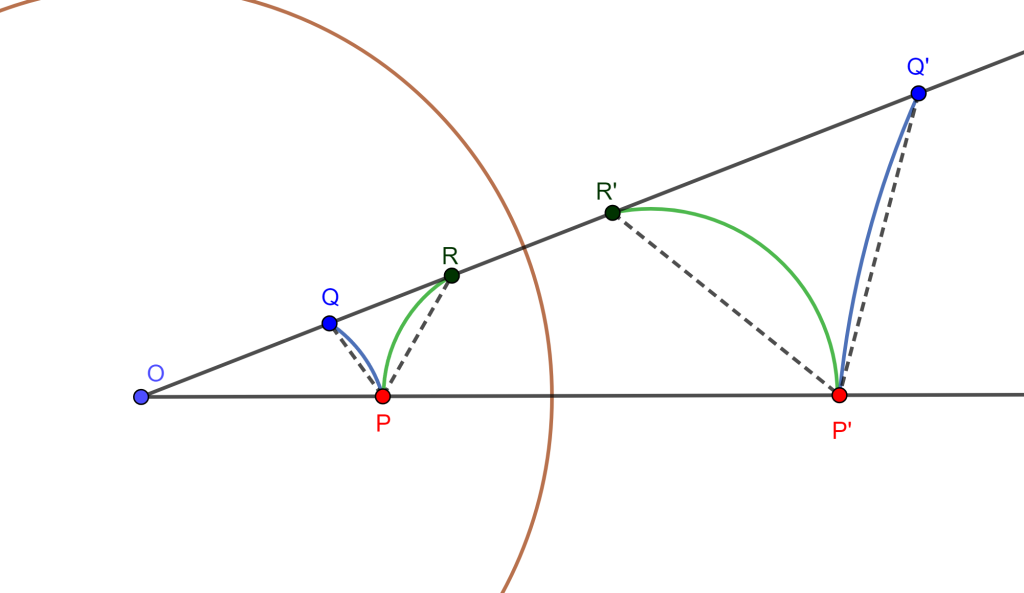
Sean 2 curvas que se intersecan en $P$ y $P\neq O$. Tracemos una línea por $OP$ y otra por $O$ que corte a las curvas en $Q$ y $R$, $OQR$ colineales.
Se tiene que $P$, $Q$ y $R$ tienen inversos $P’$, $Q’$ y $R’$ respectivamente, entonces las inversas de dichas curvas $PQ$ y $PR$ tendrán que intersecarse en $P’$, $Q’$ y $R’$ respectivamente, ahora por definición de inversión $OP\times OP’=OQ\times OQ’=OR\times OR’$, por lo cual $\triangle OPQ \approx \triangle OQ’P’$ y también $\triangle OPR \approx \triangle OR’P’$, y si trazamos las secantes que corten a las curvas en $P$ y $P’$, y que pase por $Q$, $R$, $Q’$ y $R’$, entonces

$\angle OPQ = \angle P’Q’O$, $\angle OPR = \angle P’R’O$

Y por lo cual $\angle QPR= \angle R’P’Q’$ y $\angle RPQ= – \angle R’P’Q’$, ahora si se tiene el límite cuando $Q$ y $R$ tienden a $P$, entonces $Q’$ y $R’$ tienden a $P’$, por lo cual $\angle RPQ$ y $ \angle R’P’Q’$ tienden a ser los angulos límite de la intersección de las curvas.
Por lo tanto, los ángulos preservan la inversión en magnitud pero opuestos en signo $_\blacksquare$

Observación: Es por ello que se dice que la inversión es una transformación isogonal.

Corolario 1 (Conservación de ángulos)

Si dos curvas son tangente una a la otra en $P$, sus inversas son tangentes una a la otra en $P’$.

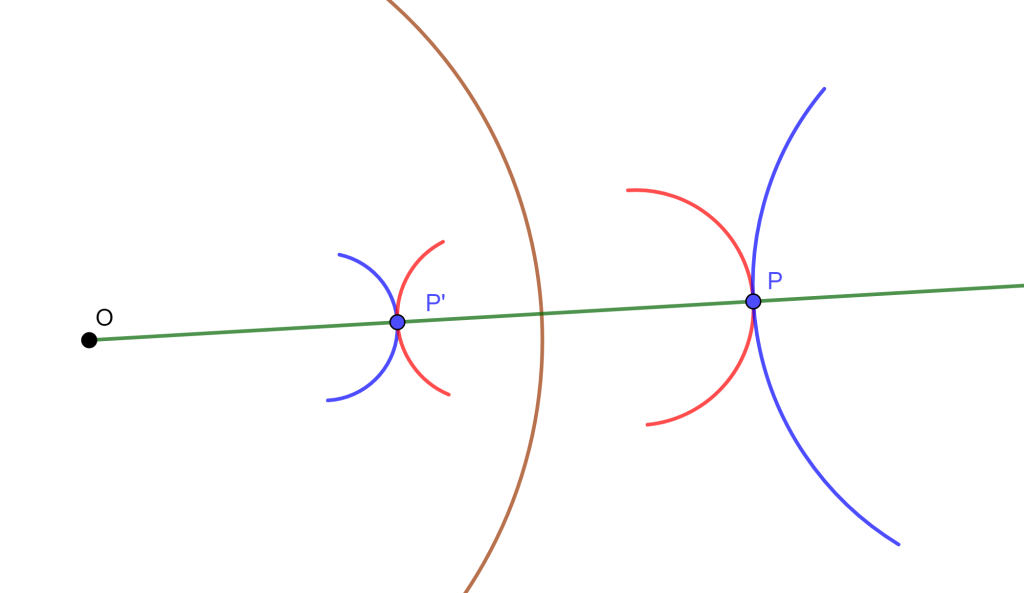
Corolario 2 (Conservación de ángulos)

Objetos ortogonales se invierten en objetos ortogonales.

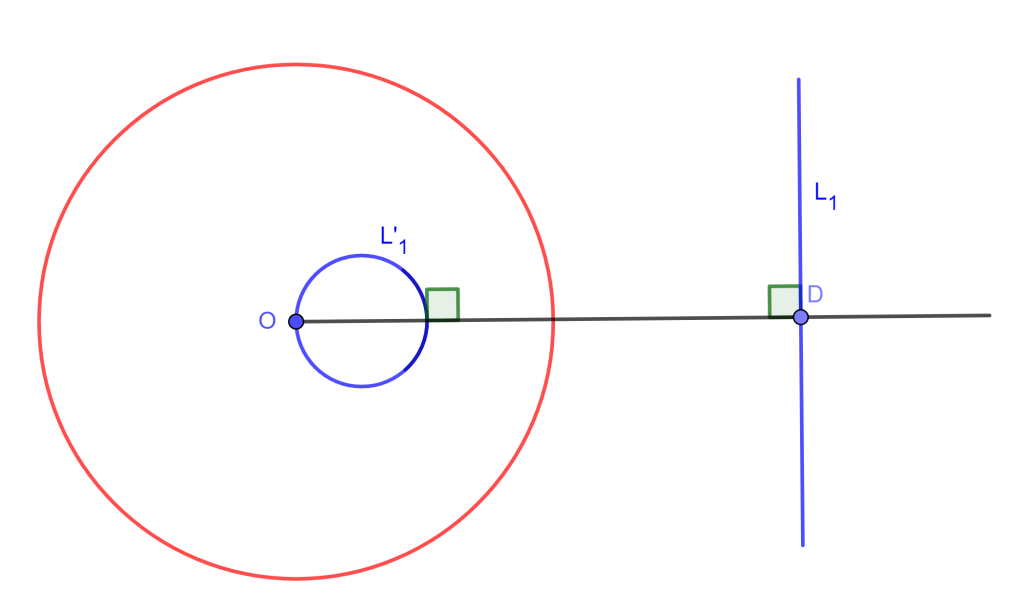
Corolario 3 (Conservación de ángulos)

Rectas paralelas se invierten en circunferencias tangentes en el centro de inversión.

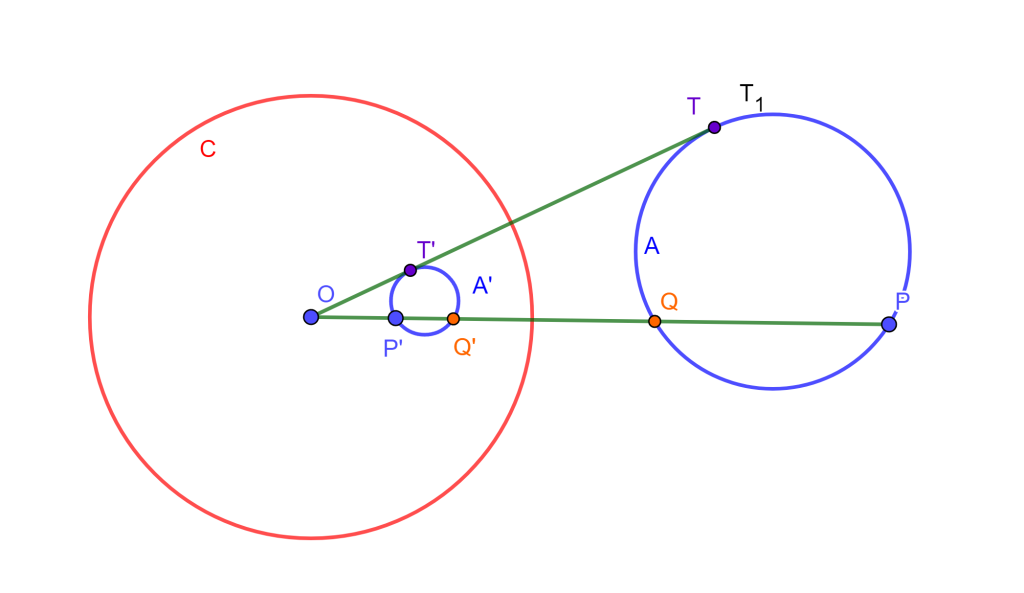
Teorema (Homotecia desde el centro de inversión)

Sea $A$ una circunferencia y $A’$ su inversa, entonces son homotéticas desde el centro de inversión.

Inversión y Distancias

Teorema

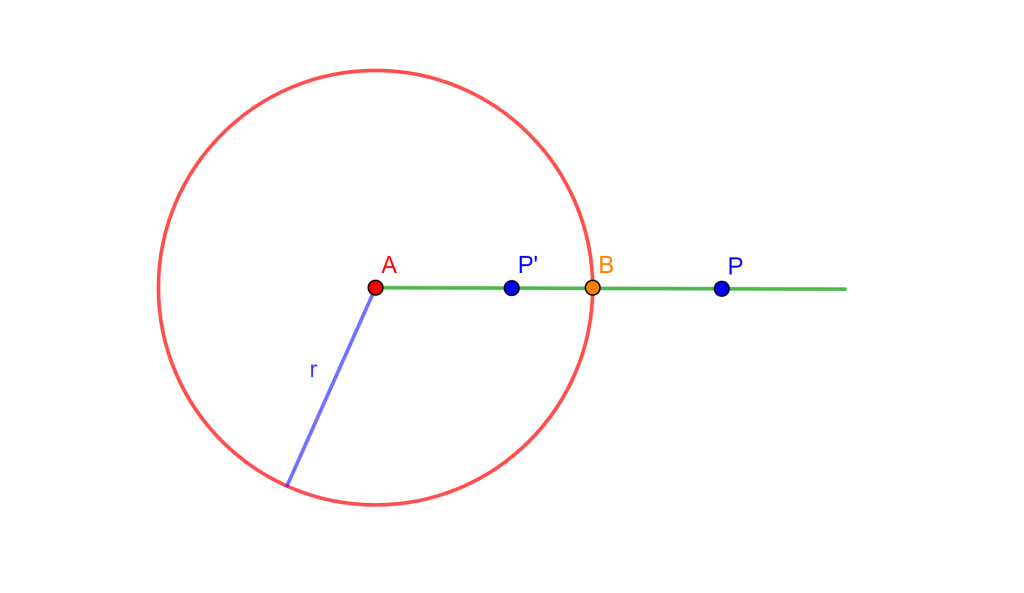
Sean $P$ y $P’$ puntos inversos y $B$ un punto colineal a $PP’$ y que corta al círculo de inversión, entonces

$BP’ = \frac{BP}{1+BP/r}$ y $BP=\frac{BP’}{1-BP’/r}$

Demostración

Se tiene que $BP’=r-OP’=r- \frac{OP’ \times OP}{OP}$, entonces por definición de inversión:

$\begin{split} BP’ & =r- \frac{r^2}{OP} \\ & =r- \frac{r^2}{r+BP} \\ & =\frac{r \times BP}{r+BP} \\ & =\frac{BP}{1+BP/r} \end{split}$

$\Rightarrow BP’= \frac{BP}{1+BP/r} $

Ahora

$\begin{split} BP & =OP-r \\ & =\frac{OP’ \times OP}{OP’} -r \\ & =\frac{r^2}{OP’} -r \\ & =\frac{r^2}{r-BP’} -r \\ & =\frac{r \times BP’}{r-BP’} \\ & =\frac{BP’}{1-BP’/r} \end{split} _\blacksquare$

Teorema

Sea $C(O,r)$ una circunferencia de inversión y $P$ y $Q$ dos puntos con inversos $P’$ y $Q’$ respectivamente, entonces

$P’Q’= \frac{r^2 \times QP}{OP \times OQ}$

Demostración

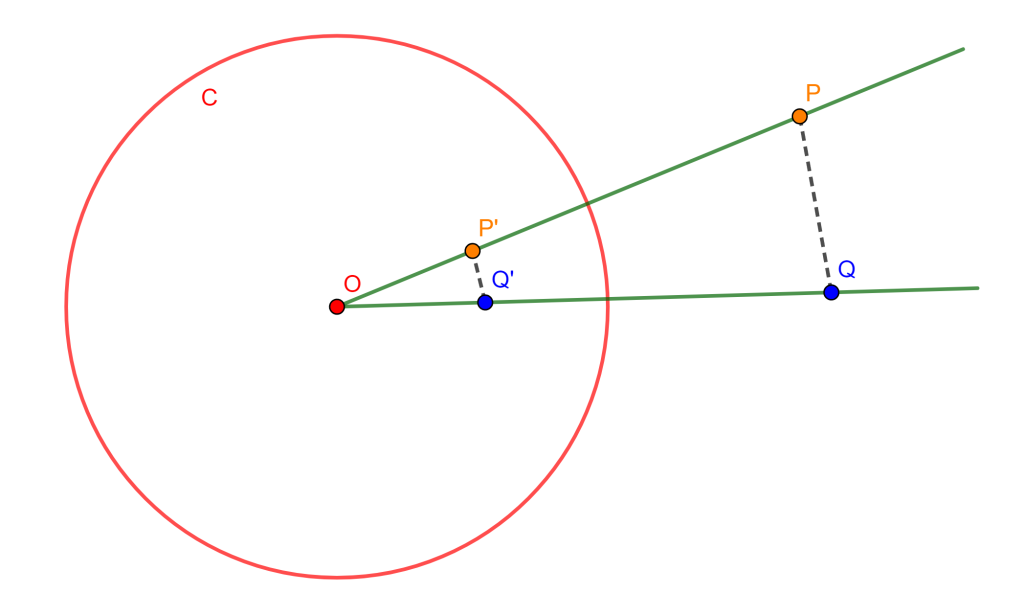
Se tiene por definición de inversión: $OP \times OP’=r^2$ y $OQ \times OQ’=r^2$

$\begin{split} & \Rightarrow OP \times OP’ = OQ \times OQ’ \\ &\Rightarrow \frac{OP}{OQ’} = \frac{OQ}{OP’} \\ & \Rightarrow \triangle OQP \approx \triangle OP’Q’ \\ & \Rightarrow \frac{OP}{OQ’} = \frac{OQ}{OP’} = \frac{QP}{P’Q’} \\ & \Rightarrow \frac{OQ}{OP’} = \frac{QP}{P’Q’} \\ & \Rightarrow P’Q’ = \frac{QP \times OP’}{OQ} \\ & \Rightarrow P’Q’ = \frac{QP \times OP’ \times OP}{OQ \times OP} \\ & \Rightarrow P’Q’ = \frac{r^2 \times QP }{OQ \times OP} \end{split} _\blacksquare$

Si $P$, $Q$ y $O$ son colineales, asumiendo $OP < OQ$ entonces

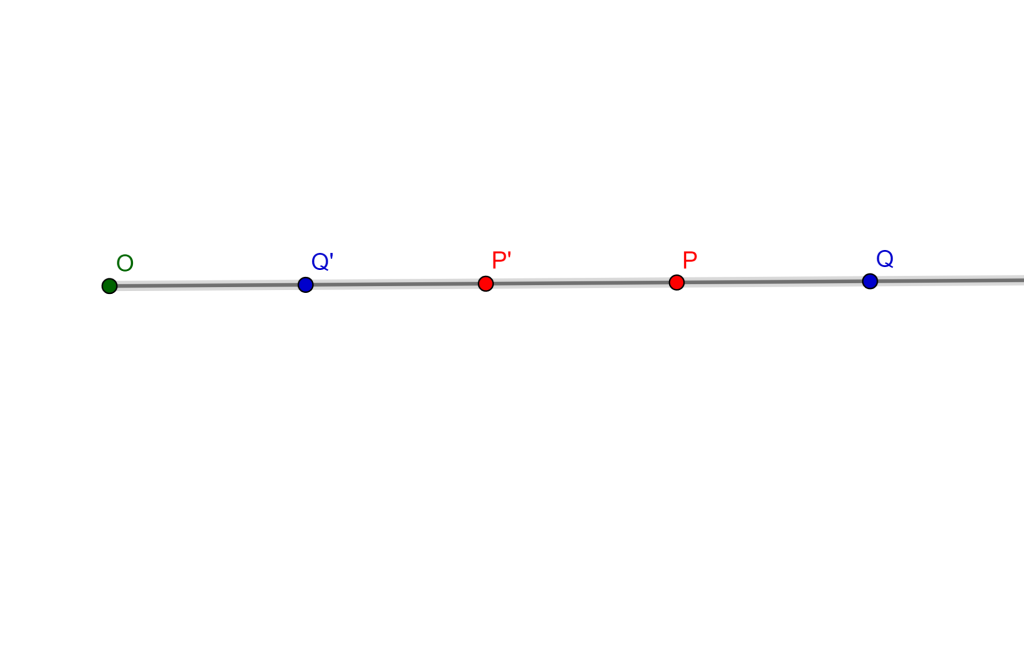
Entonces $OP \times OP’ = OQ \times OQ’$ y $P’Q’=OP’-OQ’$

$\begin{split} \Rightarrow P’Q’ & =\frac{OP \times OP’}{OP} \\ & =\frac{r^2}{OP} – \frac{r^2}{OQ} \\ & =r^2(\frac{OQ-OP}{OP \times OQ}) \\ & =\frac{r^2 \times PQ}{OP \times OQ} _\blacksquare \end{split}$

Teorema de Ptolomeo

Sea $ABCD$ un cuadrilátero cíclico convexo, entonces

$BC \times BD = BC \times AD + CD \times AB$

Demostración

Sea una circunferencia de inversión $C(A,r)$ y se tiene una circunferencia circunscrita del cuadrilátero cíclico. La circunferencia invierte los puntos en una línea, es decir, se tiene $B’$ inverso de $B$, $C’$ inverso de $C$ y $D’$ inverso de $D$, los cuales forman la línea «$L$», se muestra:

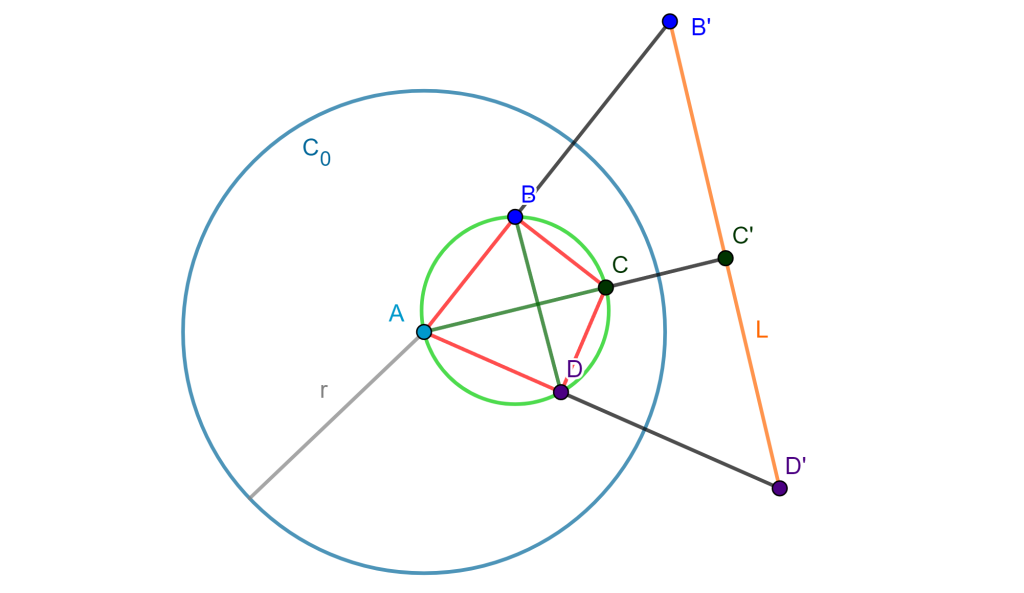
Entonces se maneja las distancias de la línea «L$, se tiene $B’D’=B’C’+C’D’$ y por el teorema anterior:

$B’D’= \frac{BD \times r^2}{AB \times AD}$, $B’C’= \frac{BC \times r^2}{AB \times AC}$ y $C’D’= \frac{CD \times r^2}{AC \times AD}$

$\Rightarrow \frac{BD \times r^2}{AB \times AD}= \frac{BC \times r^2}{AB \times AC}= \frac{CD \times r^2}{AC \times AD}$

Entonces se cancelan las $r^2$ y si nos fijamos en el denominador tenemos en comun $AB$, $AD$ y $AC$. Por lo cual multiplicamos por $AB \times AD \times AC$

$\Rightarrow \frac{BD \times AB \times AD \times AC}{AB \times AD}= \frac{BC \times AB \times AD \times AC}{AB \times AC}= \frac{CD \times AB \times AD \times AC}{AC \times AD}$

Por lo tanto, $AC \times BD = BC \times AD + CD \times AB _\blacksquare$

Teorema de Feuerbach

La circunferencia de los nueve puntos del triángulo es tangente al incirculo y a los tres excirculos.

Demostración

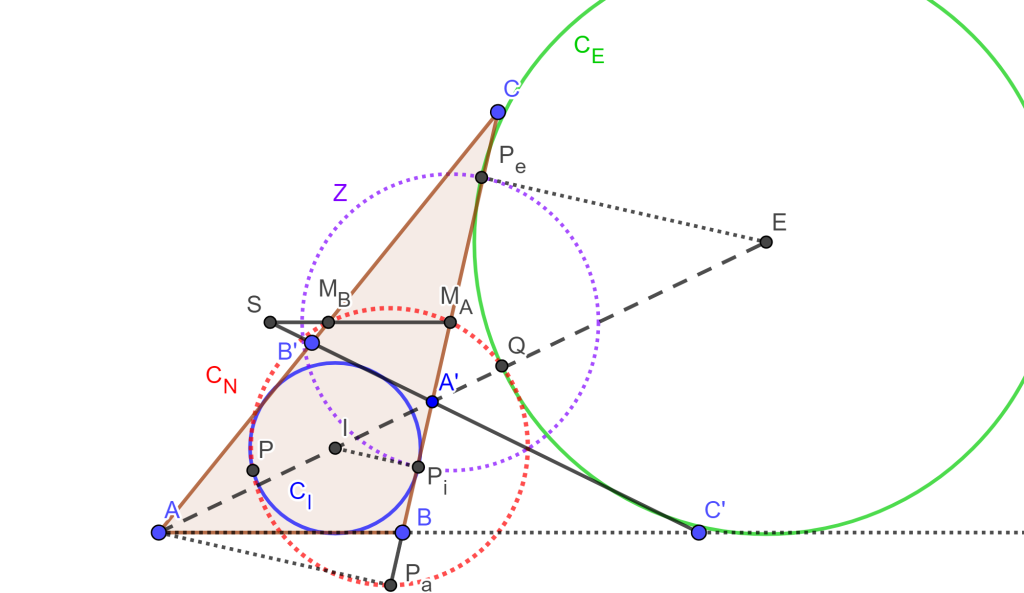
Sea el triángulo $\triangle ABC$ con $C_I$ el incirculo y $C_E$ el excirculo, sea $BC$ la tangente a $C_1$ y $C_E$, se tiene otra tangente $B’C’$ la cual es simétrica a $BC$ con respecto a la bisectriz $AI$, de lo anterior se tienen tres cosas: $C \in AB$, $B’ \in AC$ y $A’=BC \cap B’C’$.

Por otra parte, los puntos $A$ y $A’$ son centros de homotecia de $C_I$ y $C_E$ respectivamente, entonces $I_E$ es dividido por $A’$ y $A$ interna y externamente en razón de sus radios.

$\Rightarrow \frac{IA’}{A’E}=-\frac{IA}{AE}=\frac{r}{rA}$

Entonces $A$ y $A’$ son armónicos respecto a $I$ y $E$. Trazamos perpendiculares $E$, $I$ y $A$ sobre $BC$ y sus pies los llamamos $P_e$, $P_i$ y $P_a$ respectivamente, entonces los triángulos $\triangle EP_eA’ \approx \triangle IP_iA’ \approx AP_aA’$, entonces $P_a$ y $A’$ son armonicos respecto a $P_i$ y $P_e$.
Ahora sea $M_A$ punto medio de $BC$ entonces también lo es de $P_i$ y $P_e$, trazamos la circunferencia $Z$ con centro $M_A$ y radio $M_AP_i$, entonces $A’$ y $P_a$ son inversos respecto a $Z$

Por lo cual

$P_eP_i=BC-2P_iC=a-2(s-c)=c-b$

Donde $a$ es el lado opuesto al vértice $A$, de igual forma $b$ es de $B$, $c$ es de $C$ y $s$ es el semiperímetro.

Entonces el radio de $z$ es de $\frac{c-b}{2}$ y $M_AM_B=c/2$

Por lo cual $S=B’C’ \cap M_AM_B$

$\Rightarrow M_AS=M_AM_B + M_BS=M_AM_B -SM_B$, y $M_AM_B$ paralelo a $BA$ entonces $\triangle B’SM_B \approx \triangle B’C’A $ por lo cual sus lados son proporcionales $\frac{SM_B}{C’A}=\frac{M_BB’}{AB’}$.

$\Rightarrow SM_B =\frac{C’A\times B’M_B}{B’A}$

Y como $CA=C’A$ y $B’A=BA$ entonces

$SM_B=\frac{C’A\times B’M_B}{B’A}=\frac{CA(BA-M_BA)}{BA}=\frac{2bc-b^2}{2c}$

$\Rightarrow M_AS=M_AM_B-SM_B=\frac{c}{2} – \frac{2bc-b^2}{2c} = \frac{(c-b)^2}{2c}$

Así,

$M_AS \times M_AM_B = \frac{(c-b)^2}{2c} \times \frac{c}{2} = (\frac{c-b}{2})^2$

Y por lo cual $S$ y $M_B$ son inversos respecto a la circunferencia $Z$ con diámetro $P_iP_e$. El inverso de $B’C’$ es una circunferencia que pasa por $M_A$ el centro de inversión y por $P_a$ y $M_B$. Como una circunferencia está determinada por tres puntos y la circunferencia de los nueve puntos cumple esto, entonces $C_N$ es la inversa de la recta $B’C’$ con respecto a la circunferencia $Z$.
Pero el inverso de $C_I$ con respecto a $Z$ es $C_I$, al igual $C_E$ su inverso con respecto a $Z$ es $C_E$, ya que son ortogonales a $Z$; $B’C’$ es tangente a $C_I$ y $C_E$ y como la inversión conserva ángulos se sigue que la circunferencia $C_N$ será tangente a las circunferencias $C_I$ y $C_E$ (De igual forma para los otros 2 excirculos) $_\blacksquare$

Teorema (Inversión Razón Cruzada)

La razón cruzada es invariante bajo inversiones.

Demostración

(Se debe de interpretar como la razón cruzada entre puntos colineales y rectas concurrentes)

Sea, $C(O, r)$ circunferencia, $A$, $B$, $C$ y $D$ cuatro puntos colineales distintos de $O$, sus inversos $A’$, $B’$, $C’$ y $D’$ con respecto a $C$ y $a’=OA’$, $b’=OB’$, $c’=OC’$ y $d’=OD’$.

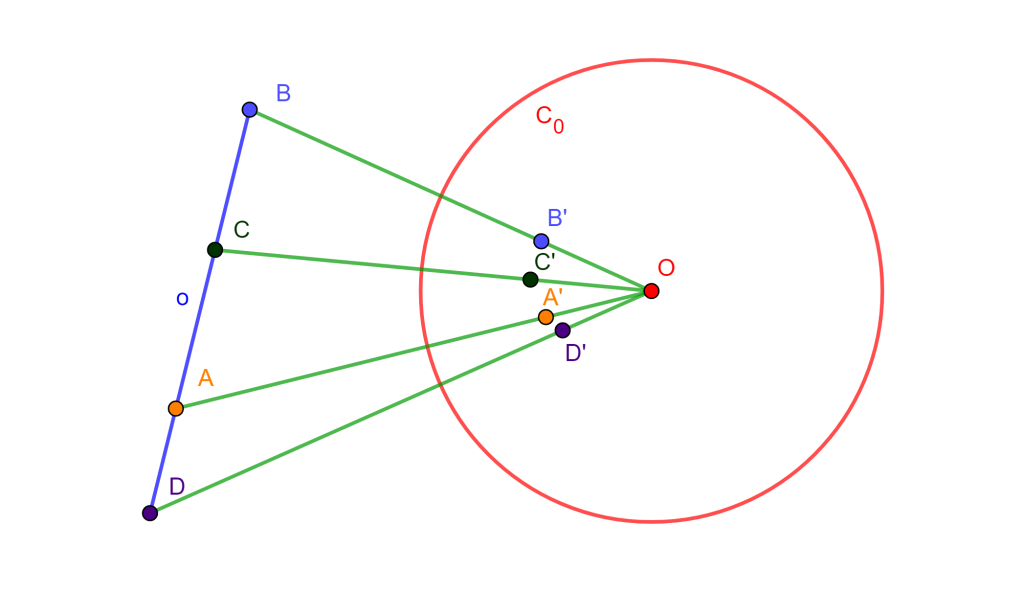
Ahora las razones cruzadas coinciden: $O(a’b’, c’d’)=o(AB, CD)$

Como la razón cruzada es una propiedad proyectiva y las inversiones respeten ángulos e invierten orientación.

$o(AB, CD)=\frac{sen \angle AOC}{sen \angle AOD} \times \frac{sen \angle DOB}{sen \angle COB}=\frac{-sen \angle A’OC’}{-sen \angle A’OD’} \times \frac{-sen \angle D’OB’}{-sen \angle C’OB’}=O(a’b’, c’d’) _\blacksquare $

Más adelante…

Se verá como la inversión es una forma alterna de resolver problemas ya demostrados y más fáciles de ver, además se revisará un tema de importante, la circunferencia de antisimilitud.

Entradas relacionadas

• Ir a Geometría Moderna II
• Entrada anterior del curso: Inversión de rectas y circunferencias
• Siguiente entrada del curso: Inversión de un Teorema y circunferencia de antisimilitud