2.2 Inversión de Rectas y Circunferencias
Introducción
De la definición de Inversión se tiene la siguiente propiedad, se tienen $P$ y $P’$ dos puntos inversos respecto a la circunferencia $C(O,r)$, y cada uno de estos describe una curva, $P$ describe a $C$ y $P’$ describe a $C’$. Estas curvas son inversas una de la otra, se les llama mutuamente inversas.
Propiedad (Curvas de Inversión)
Se tienen 2 curvas $C$ y $C’$ inversas una de la otra, las cuales se intersecan, esto lo hacen sobre la circunferencia de Inversión, debido a que el punto en común debe ser su propio inverso, y el inverso de un punto en la $C(O,r)$ es el propio punto en la circunferencia de inversión.
Dado lo anterior se puede ver la inversión aplicada a 2 objetos geométricos: Rectas y Circunferencias.
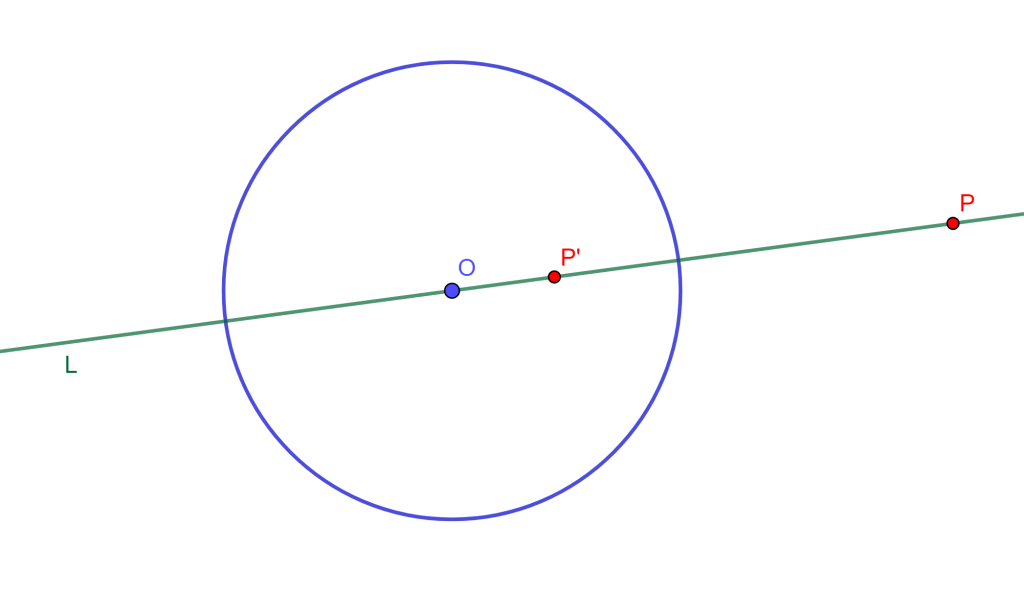
Teorema (Inversión en Recta que pasa por O)
Sea $C(O,r)$ una circunferencia de inversión y $L$ una recta que pasa por $O$, entonces el inverso de $L$ respecto a $C(O,r)$ es el mismo $L$.
Demostración
Tenemos una circunferencia $C(O,r)$ y $L$ una recta por $O$, además todo punto $P$ en $L$ tiene su inverso $P’$ tal que $O,P$ y $P’$ son colineales entonces $OP \times OP’ =r^2$.
Por lo cual los inversos de los puntos de $L$, también están en la misma recta $L$.
Por lo tanto, $L$ su inverso es el mismo $L$ $_\blacksquare$
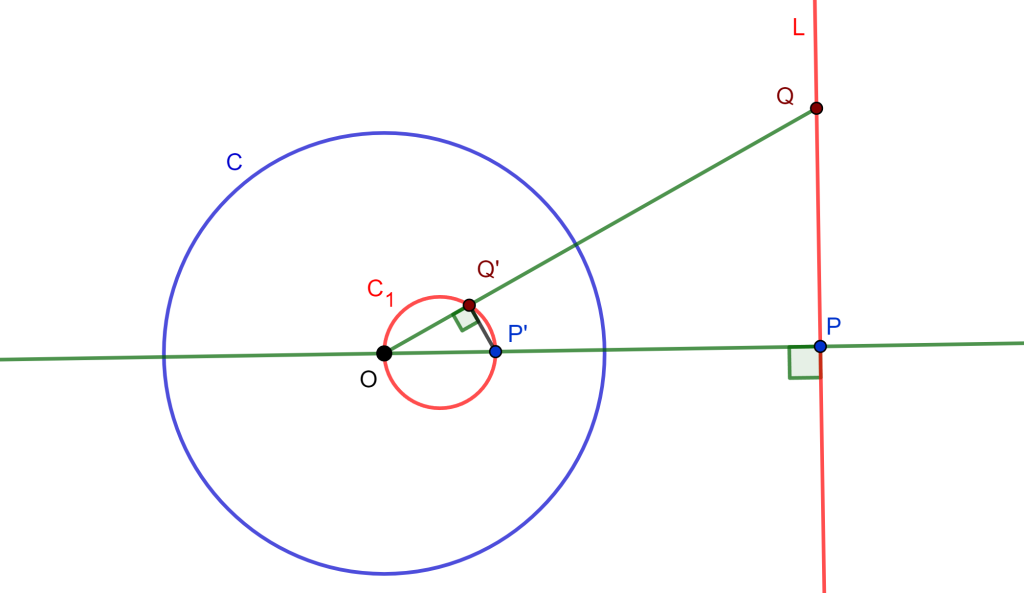
Teorema (Inversión en Recta que no pasa por O)
Sea $C(O,r)$ una circunferencia de inversión y $L$ una recta que no pasa por $O$, entonces el inverso de $L$ respecto a $C$ es una circunferencia que pasa por $O$. Recíprocamente, el inverso de una circunferencia que pasa por el centro de inversión es una recta que no pasa por el centro de inversión.
Demostración
Sea $P$ el pie de la perpendicular desde $O$ a $L$ y sea $Q \neq P$, donde $Q \in L$ y de estos obtenemos $P’$ y $Q’$ los inversos respecto a $C$ de $P$ y $Q$ respectivamente.
$\Rightarrow OP \times OP’ =r^2$ y $OQ \times OQ’=r^2$
$\Rightarrow OP \times OP’ = OQ \times OQ’$
$\Rightarrow \frac{OP}{OQ’} = \frac{OQ}{OP’}$
$\Rightarrow \triangle OQ’P’ \approx \triangle OPQ$
Esto ya que comparten 2 lados proporcionales y un ángulo en común $\angle O$.
Ahora $\triangle OPQ$ es rectángulo, entonces $\triangle OQ’P’$ es rectángulo, por lo cual $OP’$ es un diámetro de una circunferencia que pasa por $Q’$.
Análogamente, si tuviéramos un $R \in L$, $R \neq P$ y $R \neq Q$, su inverso $R’$ cumplirá $\frac{OP}{OR’} = \frac{OR}{OP’}$, con lo que $\triangle OPR \approx \triangle OR’P’$, por lo cual $\triangle OR’P’ $ es rectángulo, como $OP’$ es fijo se sigue que la circunferencia del diámetro $OP’$ que pasa por $Q’$ también pasa por $R’$.
Por lo tanto, el inverso de $L$ respecto a $C$ es $C_1$ una circunferencia que pasa por $O$ $_\blacksquare$
Inversamente, si $Q’$ es un punto de $C_1$ circunferencia, recorriendo al revés los pasos de la demostración anterior, que $Q$ está en la perpendicular a la línea del diámetro $OP’$ que pasa por el inverso de $P’$ $_\blacksquare$
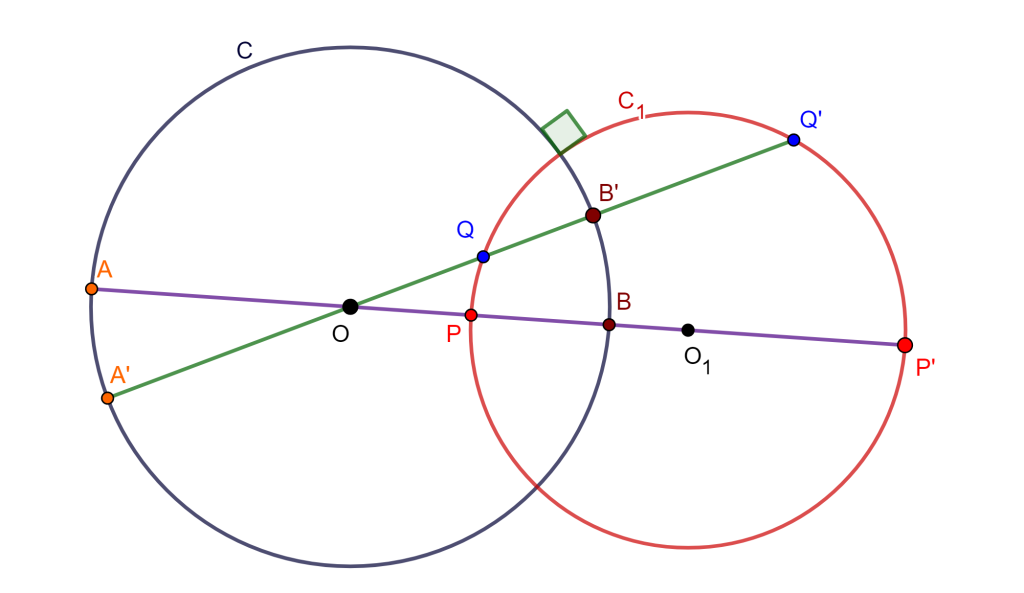
Teorema (Inversión en Circunferencia ortogonal a C(O, r))
Sea $C(O,r)$ una circunferencia de inversión y sea $C_1$ una circunferencia ortogonal a $C$, el inverso de $C_1$ es $C_1$.
Demostración
Se traza una recta que pase por $O$ y $O_1$, la cual nos genere intersecciones en $C$ las cuales son $A$ y $B$, de igual forma en $C_1$ se genera $P$ y $P’$.
Sea $C \perp C_1$ ortogonal, entonces $P$ y $P’$ son armónicos respecto a $A$ y $B$.
$\Leftrightarrow \frac{AP}{PB} = \frac{-AP’}{P’B} $
$\Leftrightarrow OP \times OP’ =r^2$
$\Leftrightarrow P$ y $P’$ son inversos respecto a $C$.
Tracemos una recta que pase por $O$ y corte a $C_1$ en $Q$ y $Q’ \in C_1$, y a $C$ en $A’$ y $B’ \in C$, tales que $Q$ y $Q’$ son armónicos respecto a $A’$ y $B’$
$\Leftrightarrow \frac{A’Q}{QB’} = \frac{-A’Q’}{Q’B’} $
$\Leftrightarrow OQ \times OQ’ =r^2$
$\Leftrightarrow P$ y $P’$ son inversos respecto a $C$.
Todo punto en una circunferencia ortogonal a la de inversión tiene su inverso en ella misma. Por lo tanto, $C_1$ es su propia inversa $_\blacksquare$
Tenemos observaciones que nos indica que los siguientes son sus propios inversos con respecto a la circunferencia de Inversión:
- La propia circunferencia de Inversión
- Rectas por el centro de Inversión
- Circunferencias ortogonales a la circunferencia de Inversión
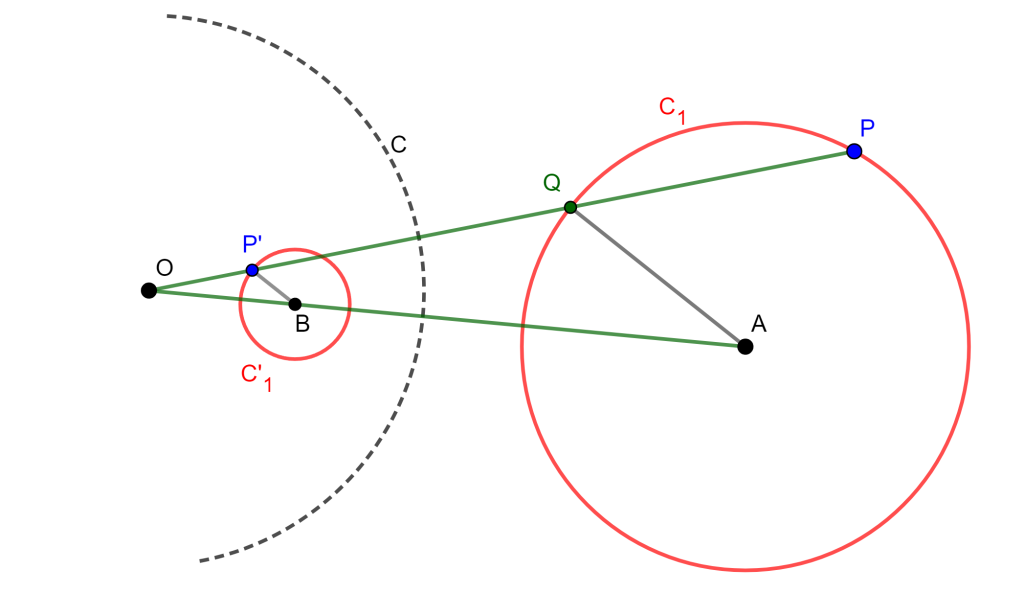
Teorema (Inversión en Circunferencia no Concéntrica con C(O, r))
El inverso de una circunferencia que no pasa por el centro de inversión, es otra circunferencia que tampoco pasa por el centro de Inversión.
Demostración
Tenemos $C_1$ una circunferencia con centro $A$, tomemos un punto $P$ sobre la circunferencia $C_1$, también tenemos $C(O,r)$ una circunferencia con centro de Inversión $O$.
Tracemos una recta $OP$, genera un punto de intersección $Q$, y se genera $P’$ inverso de $P$. Ahora tracemos la recta $OA$ y $QA$, además tracemos una paralela a $QA$ que interseque a $OA$ en $B$
Por definición de Inversión $OP \times OP’=r^2$ y $OQ \times OP = w$, ahora como los triángulos $\triangle OBP’$ y $\triangle OAQ$ son semejantes, entonces
$\Leftrightarrow \frac{OP’}{OQ} = \frac{OB}{OA}=\frac{BP’}{AQ} $
$\Leftrightarrow \frac{OP’}{OQ} = \frac{OB}{OA} $
$\Leftrightarrow OB=\frac{OP’ \times OA}{OQ} $ como $OQ = w/OP$
$\Leftrightarrow OB=\frac{OP’ \times OA}{w/OP} =\frac{OP’ \times OP\times OA}{w}=\frac{r^2 \times OA}{w} $
Entonces $OB$ es constante, $B$ es un punto fijo y $BP’$ es finita y constante, entonces el lugar geometrico de $P’$ es una circunferencia $C’_1$, por lo cual el punto $P’$ no pasa por $O$.
Por lo tanto, el Inverso de $C_1$ es $C’_1$ $_\blacksquare$
Observación: Note que $P$ y $P’$ son puntos antihomologos, $Q$ y $P’$ son homólogos y $O$ es el centro de homotecia de las circunferencias $C_1$ con centro $A$ y $C’_1$ con centro $B$.
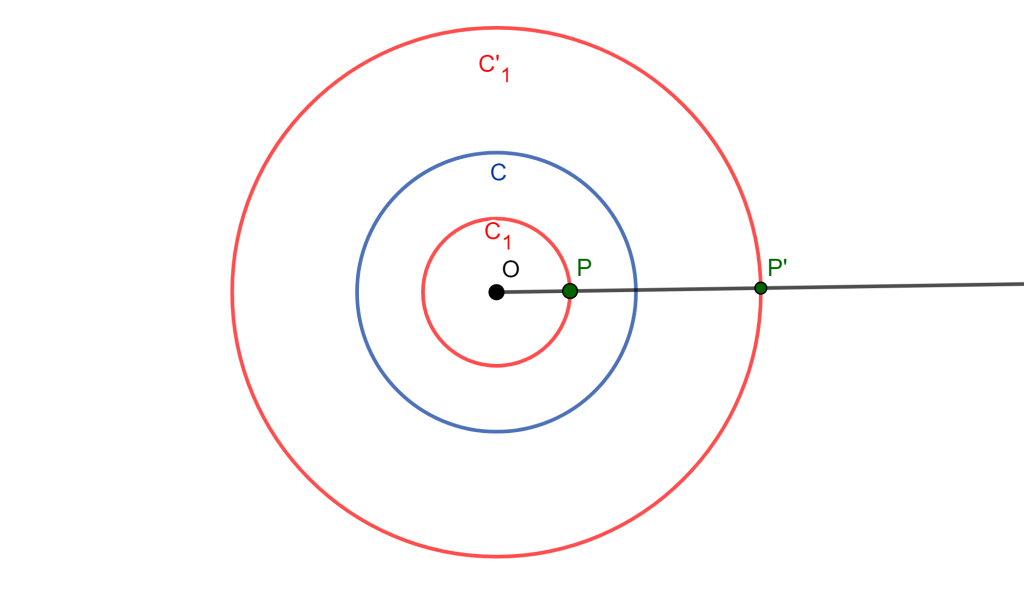
Teorema (Inversión en Circunferencia Concéntrica con C(O, r))
El inverso de una circunferencia concéntrica con la circunferencia de inversión, es otra circunferencia concéntrica con la circunferencia de inversión.
Demostración
Sea $C(O,r)$ nuestra circunferencia de Inversión y $C_1$ una circunferencia concéntrica a $C$
Tomemos un punto en $C_1$ el cual es $P$, del cual su inverso es $P’$ con respecto a $C(O,r)$, entonces la distancia $OP$ es constante, al igual $r$ es constante y por definición de inversión $OP \times OP’ =r^2$ entonces $OP’=r^2/OP$ por lo cual $OP’$ es constante.
Por lo tanto, el inverso de $C_1$ es una circunferencia $C’_1$ con centro $O$ y radio $OP’$ $_\blacksquare$
Más adelante…
Otro aspecto a analizar de la inversión será la conservación de ángulos.
Entradas relacionadas
- Ir a Geometría Moderna II
- Entrada anterior del curso: Puntos Inversos con respecto a una circunferencia
- Siguiente entrada del curso: Conservación de ángulos