Introducción

La definición de límite de una función suele ser uno de los conceptos más retadores dentro del cálculo y es por ello que, antes de entrar a su análisis formal, queremos dar una introducción con la finalidad de desarrollar la intuición necesaria para lograr el entendimiento de esta definición.

Idea intuitiva de límite de una función

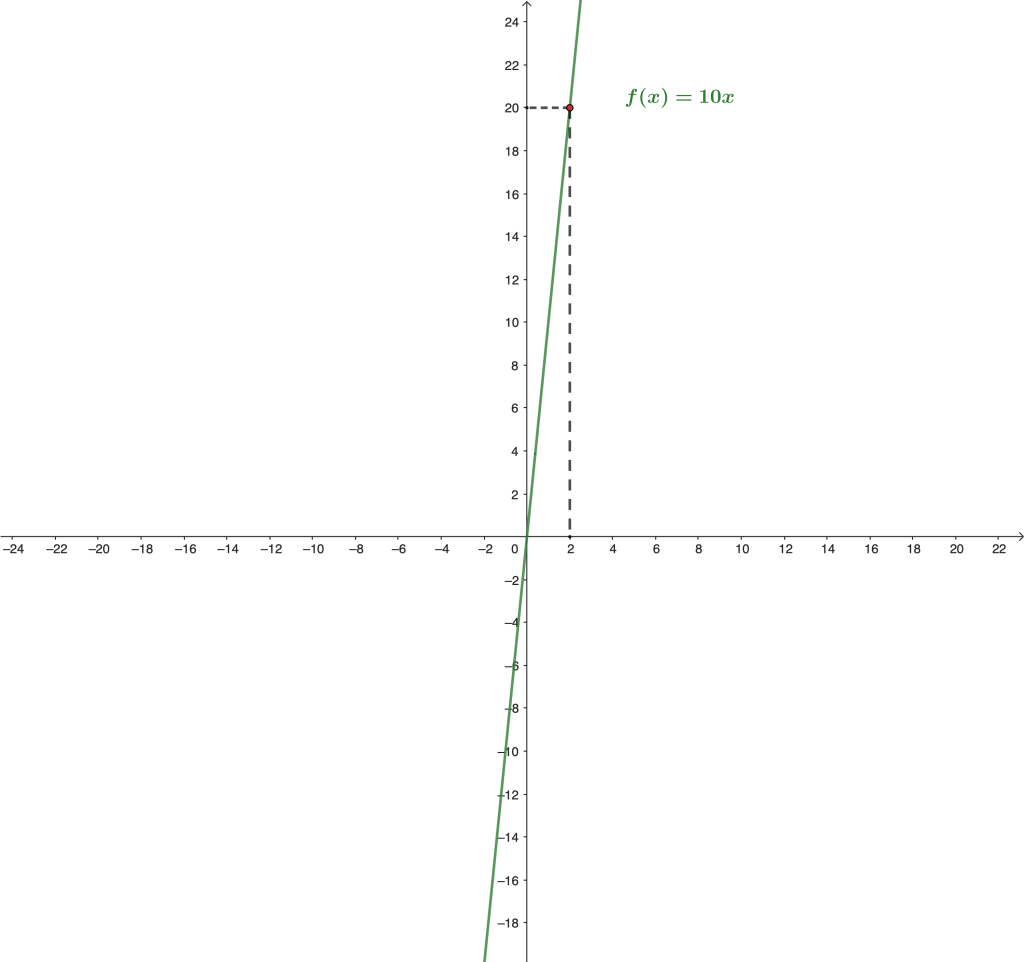
Consideremos la función $f:\mathbb{R}\to \mathbb{R}$ tal que $f(x)=10x$.

En la gráfica de la función $f(x)=10x$, podemos observar que si $x$ toma valores cercanos a $2$, entonces $f(x)$ se aproxima a $20$. ¿Pero qué tanto es posible aproximar los valores de la función $f(x)$ a $20$?

Por ejemplo, ¿podemos encontrar un valor de $x$ distinto de $2$ tal que $f(x)$ esté a una distancia de $20$ menor que $12$ , es decir, $|f(x)–20|<12$?

Consideremos $x=1$. De esta forma, $f(1)=10$ y $|f(1)–20|=|10–20|=10<12$.

¿Podemos encontrar un valor de $x$ distinto de $2$ tal que $f(x)$ esté a una distancia de $20$ menor que $1$, es decir, $|f(x)–20|<1$?

Si tomamos $x=1.99$, se tiene que $|f(1.99)–20|=|19.9–20|=0.1<1$.

Hasta este momento, se han encontrado valores puntuales de $x$ que permiten que $f(x)$ se aproxime a $20$. Sin embargo, existen más valores de $x$ que lo pueden cumplir. Retomando la última aproximación deseada, podemos ver que $x=2.02$ también cumple el propósito, pues $|f(2.02)–20|=|20.2-20|=0.2<1$. En realidad, es posible hallar todo un intervalo que lo cumpla.

Para poder obtener dicho intervalo, procedemos estableciendo la desigualdad deseada

$$\begin{array}{cc}& |f(x)–20|<1.\\ \\ \iff & |10x–20|<1.\\ \\ \iff & \frac{|10x–20|}{10}<\frac{1}{10}.\\ \\ \iff & |x–2|<\frac{1}{10}.\end{array}$$

Lo anterior indica que para que $f(x)$ esté a una distancia de $20$ menor que $1$, entonces $x$ debe estar a una distancia de $2$ menor que $\frac{1}{10}$.

¿Podemos encontrar un valor de $x$ distinto de $2$ tal que $f(x)$ esté a una distancia de $20$ menor que $\epsilon >0$, es decir, $|f(x)–20|<\epsilon$?

Análogamente, se obtiene que para que $|f(x)-20|<\epsilon$, entonces $|x-2|<\frac{\epsilon }{10}$. Generalizando más, podemos notar que para cualquier $x_0\in \mathbb{R}$ se tiene que $|f(x)-10x_0|<\epsilon$ con $x\ne x_0$, siempre que $|x-x_0|<\frac{\epsilon }{10}.$

En la siguiente entrada se proporcionará la definición formal del límite. Sin embargo, de forma provisional para esta entrada, diremos que $L\in \mathbb{R}$ es el límite de la función $f$ en $x_0$ si la distancia entre $f(x)$ y $L$ es menor que un número $\epsilon >0$ elegido de antemano cuando $x$ se aproxima a $x_0$, pero es distinto de $x_0$.

Considerando lo anterior para nuestro ejemplo, se tiene que el límite de $f$ en $x_0=2$ es $L=20$.

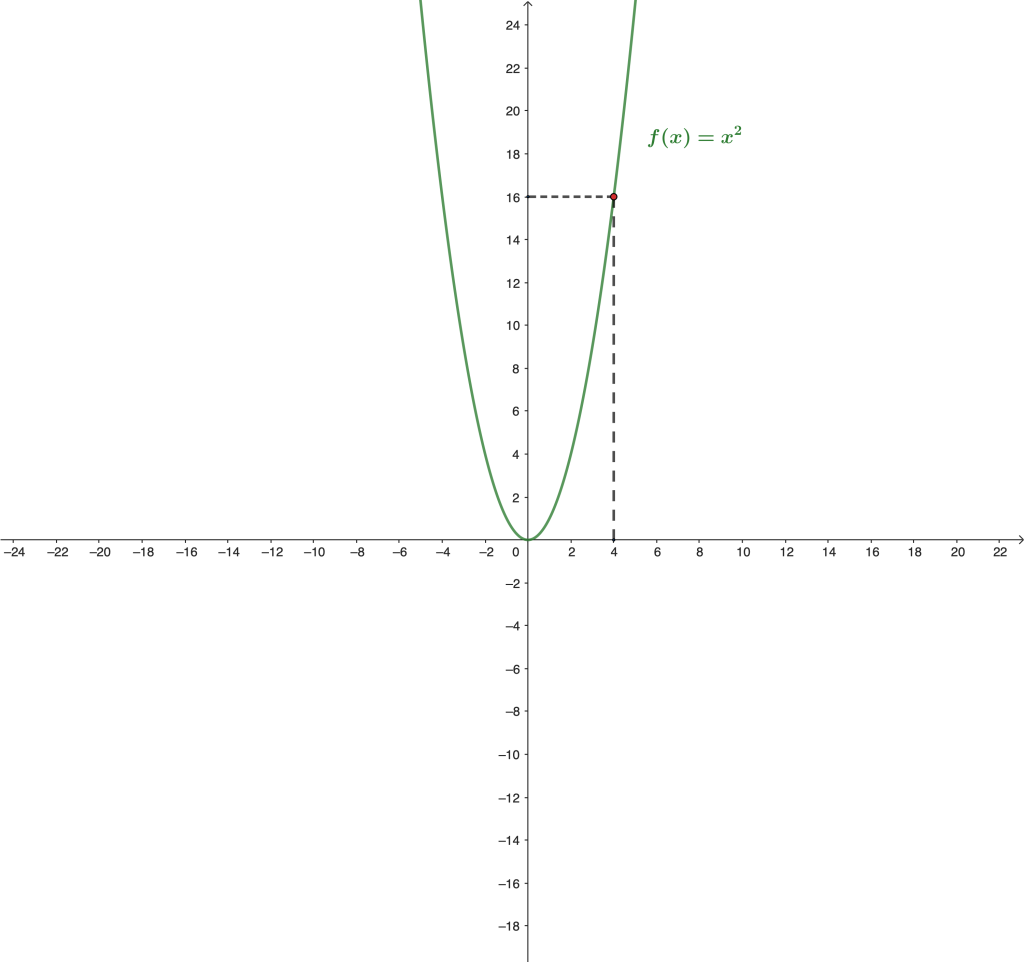
Usemos como segundo ejemplo la función $f:\mathbb{R}\to \mathbb{R}$ tal que $f(x)=x^2$.

Veremos que el límite de $f$ en $x_0=4$ es $L=16$. Para ello, notemos que

$$\begin{array}{cc}& |f(x)–16|<\epsilon .\\ \iff & |x^2–16|<\epsilon .\\ \iff & |(x-4)(x+4)|<\epsilon .\\ \iff & |x-4||x+4|<\epsilon .\end{array}$$

A diferencia del caso anterior, parece que no es tan directo llegar a nuestro objetivo, pero notemos que particularmente podemos pedir que $|x-4|<1$, entonces

$$\begin{array}{cc}& -1<x-4<1.\\ \iff & 3<x<5.\\ \iff & 7<x+4<9.\end{array}$$

En resumen, si $|x-4|<1$, entonces $|x+4|<9$. Lo cual implica que
$$|x^2–16|=|x-4||x+4|<9|x-4|.$$
Si además restringimos la distancia de $x$ respecto a $4$ de tal manera que $|x-4|<\frac{\epsilon }{9}$ y retomando la expresión anterior llegamos a lo siguiente:

$$\begin{array}{c}|x^2–16|=|x-4||x+4|<9|x-4|<9\cdot \frac{\epsilon }{9}=\epsilon .\\ \therefore |x^2–16|<\epsilon .\end{array}$$

Esto siempre que $|x-4|$ sea menor que $1$ y $\frac{\epsilon }{9}$, es decir, siempre que $|x-4|<min\{1,\frac{\epsilon }{9}\}$.

De los dos ejemplos revisados en esta entrada, podemos notar que logramos que $f(x)$ se aproxime a $L$ con una distancia menor de épsilon cuando $x$ está lo suficientemente cerca de $x_0$. Para lograr esto último, acotamos $x-x_0$ en términos de un valor positivo que depende de $\epsilon$ (para el primer ejemplo fue $\frac{\epsilon }{5}$ y para el segundo $min\{1,\frac{\epsilon }{9}\}$). Vale la pena entonces darle un nombre a este valor positivo: $\delta$.

Parafraseando: Logramos que $f$ se aproxime arbitrariamente, dado $\epsilon >0$, a $L$ cuando $x$ está lo suficientemente cerca, $\delta >0$, de $x_0$.

Obtenemos así un indicio muy importante, para probar que $L$ es el límite de $f$ en $x_0$, habrá que dar un valor arbitrario fijo y positivo $\epsilon >0$ para el cual necesitaremos encontrar otro valor positivo, $\delta >0$, tal que si $|x-x_0|<\delta$, entonces se cumpla que $|f(x)-L|<\epsilon$. Adicionalmente, se pide que $x\ne x_0$, tal condición puede ser compactada de la siguiente forma $0<|x-x_0|<\delta$, pues que la distancia entre $x$ y $x_0$ sea mayor que cero implica directamente que son distintos.

Antes de finalizar con esta entrada, es conveniente aclarar que no siempre tendremos funciones tan amigables en las cuales podamos evaluar directamente el valor de $x_0$ en $f$ para encontrar $L$. Incluso habrá ocasiones en las cuales no nos podamos aproximar de la manera en la que lo hicimos en estos ejemplos, pero por ahora no daremos muchos detalles extra al respecto, será tema para entradas posteriores.

Más adelante…

En la siguiente entrada daremos la definición formal de límite de una función y veremos varios ejemplos de funciones cuyo límite existe. Una vez dominemos la definición podremos incursionar en varias de sus propiedades y podremos tomar ventaja de estos conocimientos para tener una mayor comprensión sobre el comportamiento de diversas funciones de interés.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Para corroborar que la idea intuitiva de límite de una función se ha comprendido, se queda como ejercicio realizar un análisis similar al expuesto en esta entrada. Consideremos la función $f(x)=4x^2$ definida para todo $x\in \mathbb{R}$. En este caso, tomaremos $x_0=3$ y $f(x_0)=4(3{)}^2=36.$

• Grafica $f(x)$.
• Encuentra un valor de $x$ tal que $|f(x)-36|<30$.
• Encuentra un valor de $x$ tal que $|f(x)-36|<1$.
• Encuentra un intervalo de $x$ alrededor de $x_0=3$ tal que $|f(x)-36|<\frac{1}{100}$.
• Encuentra un intervalo de $x$ alrededor de $x_0=3$ tal que $|f(x)-36|<\epsilon$, con $\epsilon >0$.

Entradas relacionadas

• Ir a Calculo Diferencial e Integral
• Entrada anterior del curso: El número de Euler
• Siguiente entrada del curso: Definición formal de límite de una función
• Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»