Introducción

Quizás en algunos de tus cursos anteriores te presentaron funciones parecidas a las siguientes:
$$\begin{array}{rlrlrl}f(x)& =4x^2-3x+1,& t(x)& =\frac{x^2+2x+5}{x^3+3},& k(x)& =x^3\text{.}\end{array}$$
Todas pertenecen al conjunto de las funciones algebraicas. A lo largo de esta entrada, veremos las definiciones formales para cada una y comenzaremos a realizar un análisis geométrico con este conjunto de funciones.

Funciones polinomiales

Definición (función polinomial): Sea $f$ una función. Decimos que $f$ es una función polinomial si está definida como:
$$p(x)=a_n{x}^n+a_{n-1}{x}^{n-1}+\dots +a_0$$
donde $n\in \mathbb{N}\cup \left\{0\right\}$ y los coeficientes $a_i\in \mathbb{R}$.

Definición (grado de una función polinomial): Llamamos grado de p(x) a la potencia mayor de $x$ con un coeficiente $a_i\ne 0$.
Ejemplos:

• $g(x)=120x^{10}+34x^6+14$
  el grado de $g(x)$ es $10$
• $h(x)=\pi x^3+2\pi x^2+x$
  el grado de $h(x)$ es $3$

Una observación importante es que las funciones del tipo $f(x)=x^n$ con $n\in \mathbb{N}$, mejor conocidas como potencias de $x$, son un caso particular de las funciones polinomiales.

Funciones racionales

Definición (función racional): Consideremos $g$ una función. Diremos que $g$ es una función racional si está definida como el cociente de dos polinomios:
$$g(x)=\frac{a_n{x}^n+a_{n-1}{x}^{n-1}+\dots +a_0}{b_n{x}^n+b_{n-1}{x}^{n-1}+\dots +b_0}$$
donde $n\in \mathbb{N}\cup \left\{0\right\}$, los coeficientes $a_i,b_i\in \mathbb{R}$ y $b_n{x}^n+b_{n-1}{x}^{n-1}+\dots +b_0\ne 0$.

Ejemplos:

• $$h(x)=\frac{x^2-1}{x+3}$$
• $$g(x)=\frac{x}{x^3+1}$$

Análisis geométrico

En numerosas ocasiones tendremos la necesidad de realizar un bosquejo de la gráfica de una función. Para ello nos basaremos en la gráfica de una función conocida previamente y la siguiente serie de elementos donde consideremos a $f(x)$ una función en los reales y a $\alpha$ una constante:
Traslaciones

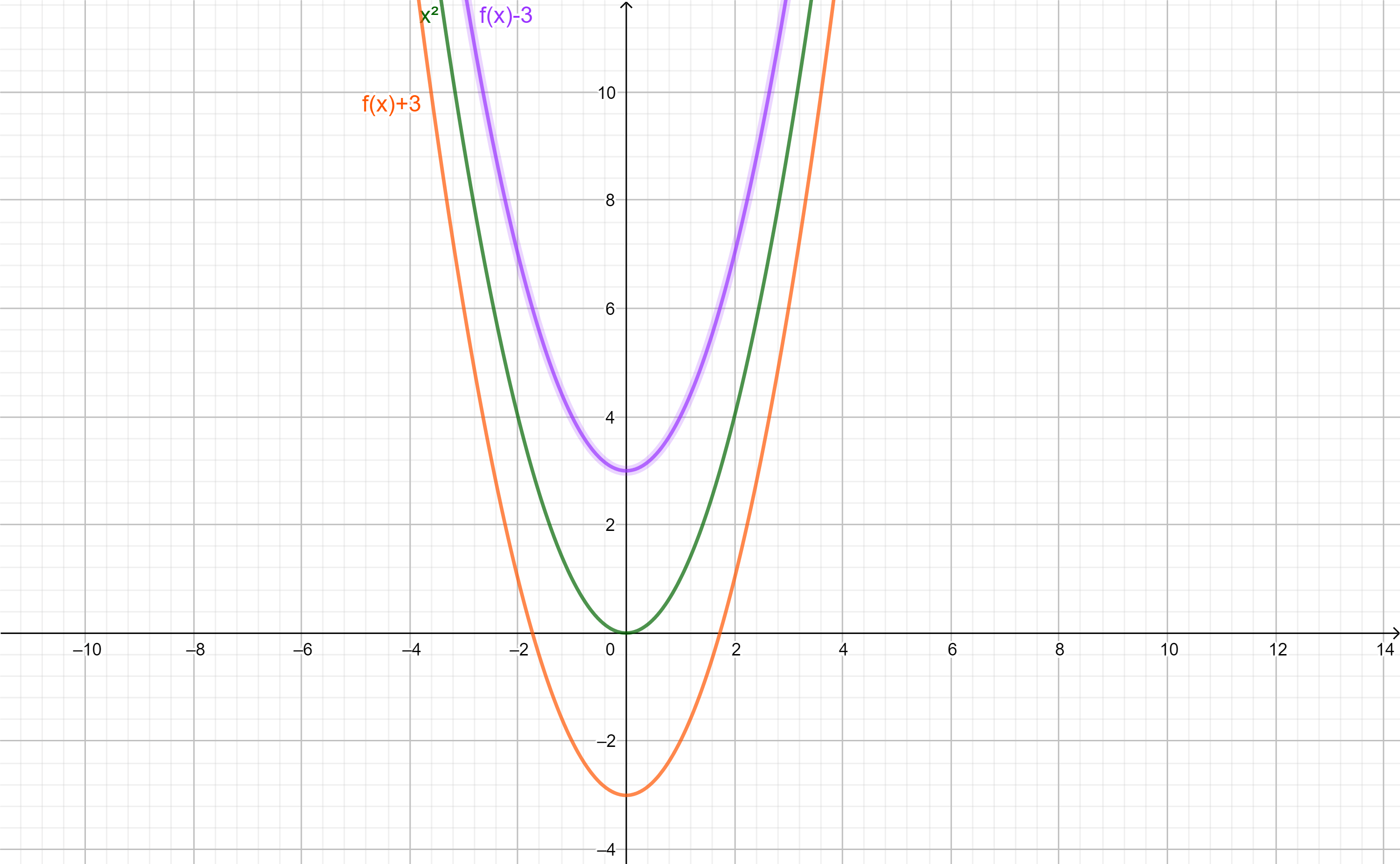
• Para $h(x)=f(x)+\alpha$ con $\alpha >0$ tenemos que la gráfica de $h$ es la gráfica de $f$ trasladada verticalmente $\alpha$ unidades hacia arriba (sobre el eje $y$).
• Y para $h(x)=f(x)-\alpha$ con $\alpha >0$ la gráfica de $h$ es la gráfica de $f$ trasladada verticalmente $\alpha$ unidades hacia abajo (sobre el eje $y$).
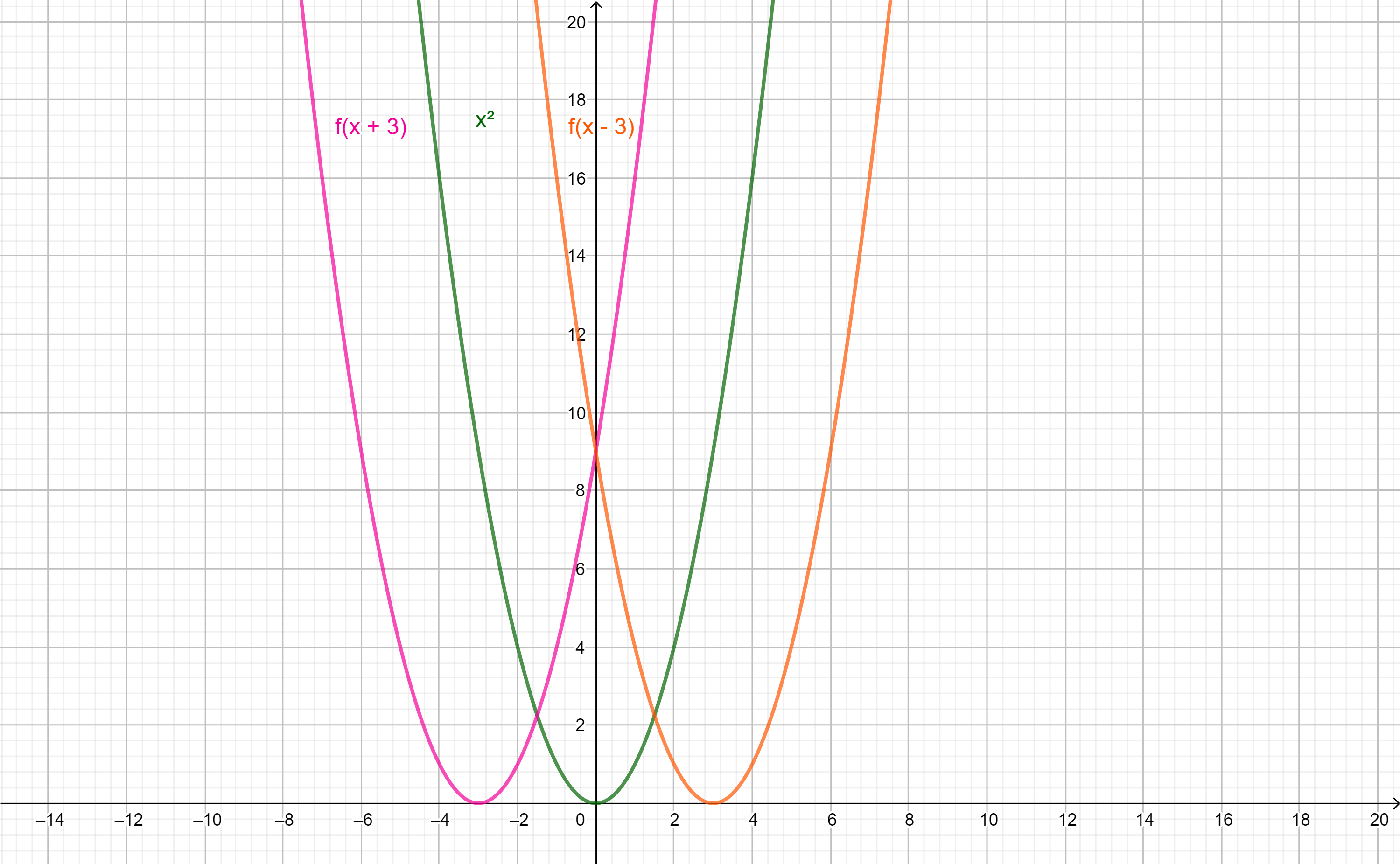
• Ahora si $h(x)=f(x-c)$ con $\alpha >0$ entonces la gráfica de $h$ sería la gráfica de $f$ trasladada horizontalmente $\alpha$ unidades hacia la derecha (sobre el eje $x$).
• En cambio si $h(x)=f(x+c)$ con $\alpha >0$ entonces la gráfica de $h$ sería la gráfica de $f$ trasladada horizontalmente $\alpha$ unidades hacia la izquierda (sobre el eje $x$).

Consideremos los siguientes ejemplos para $f(x)=x^2$:

Ampliaciones y reducciones

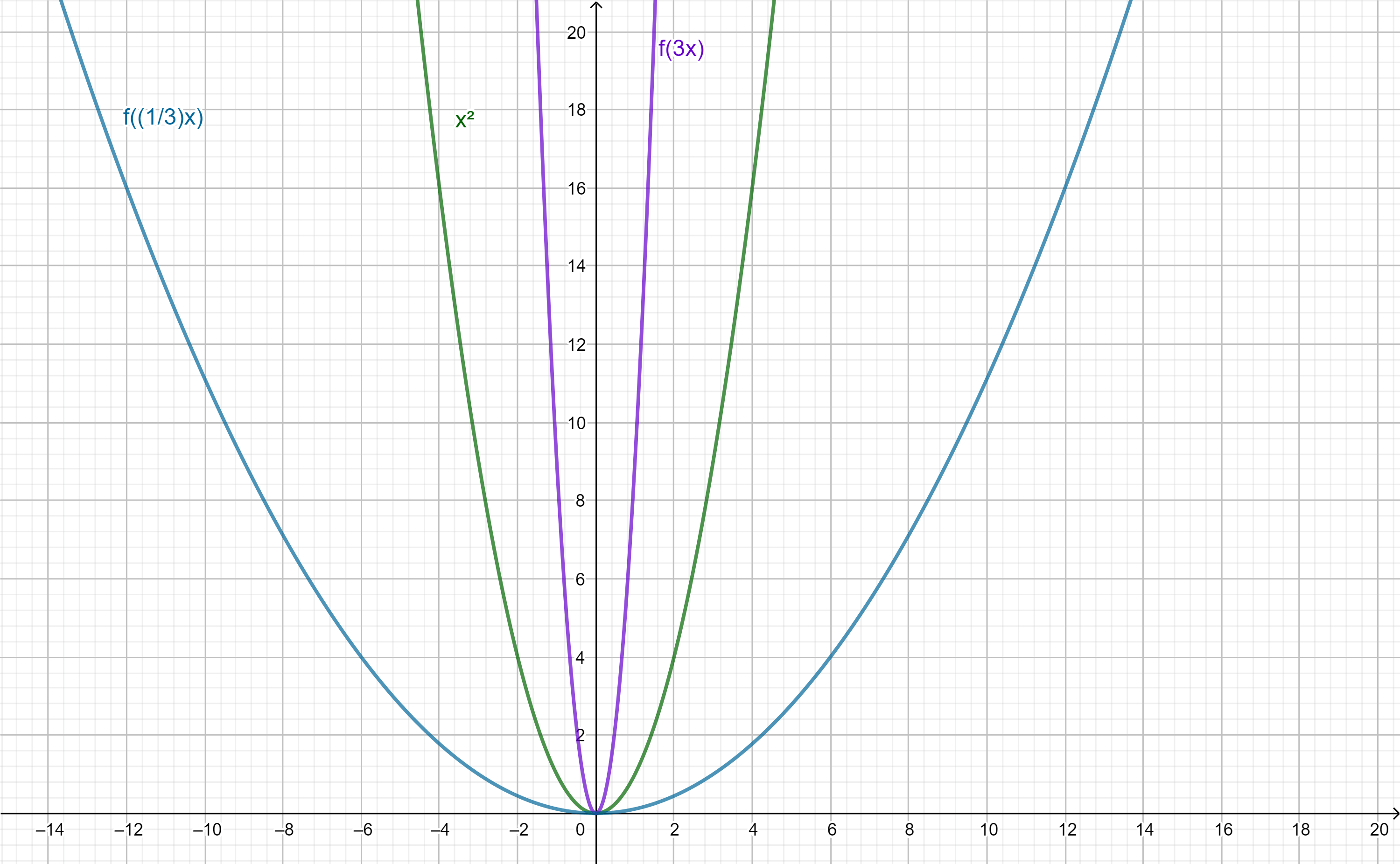
• Si $g(x)=f(\alpha x)$ con $\alpha >1$ su gráfica sería la gráfica de $f$ comprimida horizontalmente (sobre el eje $x$).
• Para $g(x)=f(\alpha x)$ con $0<\alpha <1$ su gráfica sería la gráfica de $f$ expandida horizontalmente (sobre el eje $x$).
• Y para $g(x)=f(\alpha x)$ con $\alpha <-1$ su gráfica sería la gráfica de $f$ comprimida horizontalmente (sobre el eje $x$) y reflejada respecto del eje $y$.
• Finalizamos con $g(x)=f(\alpha x)$ con $-1<\alpha <0$ su gráfica sería la gráfica de $f$ expandida horizontalmente (sobre el eje $x$) y reflejada respecto del eje $y$.

Observación: Si $\alpha =1$ vemos que $f((1)x)=f(x)$ por lo que no hay cambios.

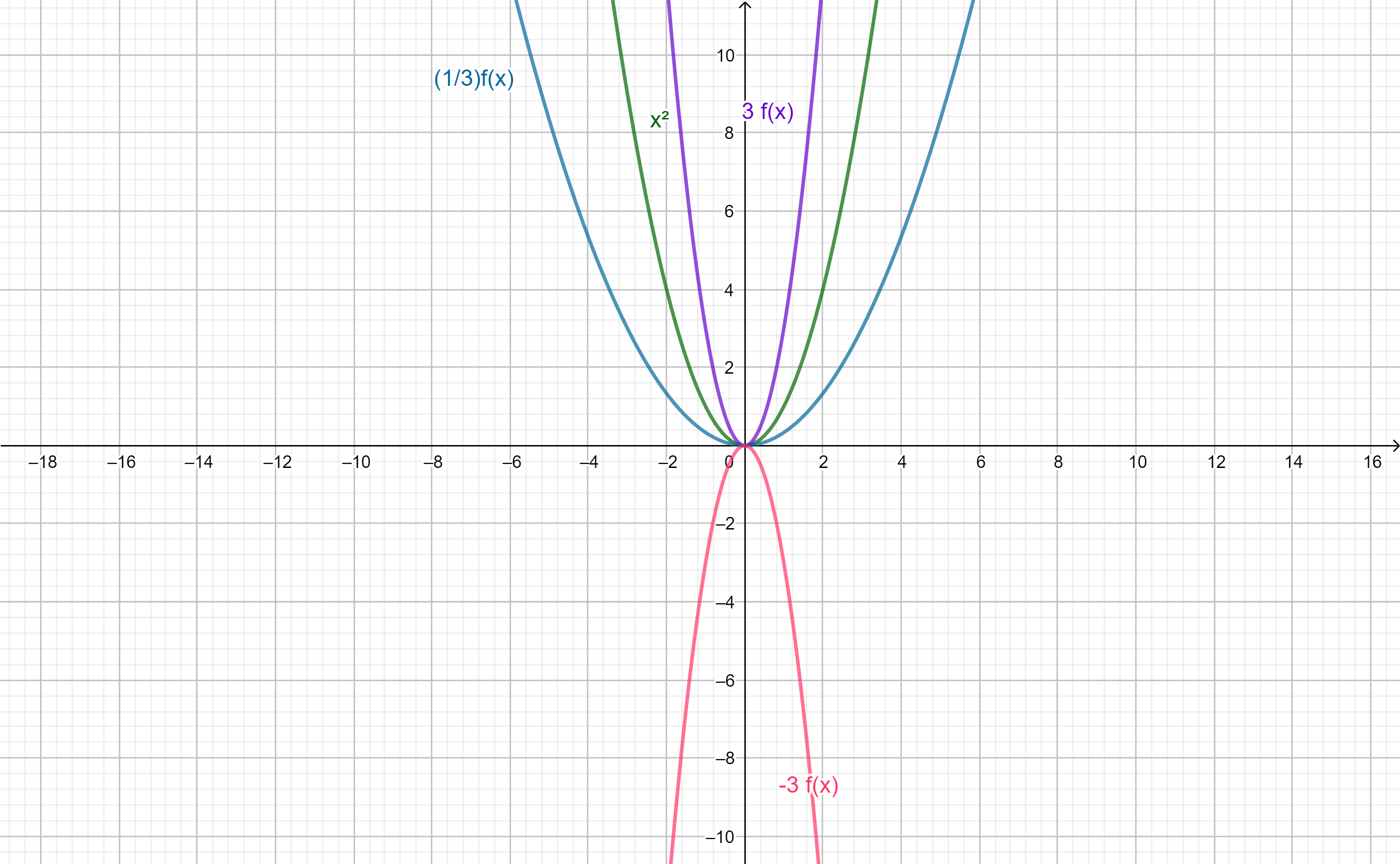
• Ahora bien si $g(x)=\alpha f(x)$ donde $\alpha >1$ la gráfica de $g$ es la gráfica de $f$ expandida verticalmente (sobre el eje $y$).
• Cuando $g(x)=\alpha f(x)$ donde $0<\alpha <1$ la gráfica de $g$ es la gráfica de $f$ comprimida verticalmente (sobre el eje $y$).
• Si $g(x)=\alpha f(x)$ donde $-1<\alpha$ la gráfica de $g$ es la gráfica de $f$ expandida verticalmente (sobre el eje $y$) y reflejada respecto del eje $x$.
• Para $g(x)=\alpha f(x)$ donde $-1<\alpha <0$ la gráfica de $g$ es la gráfica de $f$ comprimida verticalmente (sobre el eje $y$) y reflejada respecto del eje $x$.

Observación: Para $\alpha =1$ tenemos que $(1)(f(x))=f(x)$.

Hablemos sobre la función inversa

Recordemos que si tenemos $f:A\to B$ una función esto significa que:
$$Graf(f)=\{(x,f(x)):x\in A\}\text{.}$$

Ahora si consideramos a $f$ una función invertible, vemos que para $f^{-1}:B\to A$ ocurre:
$$Graf(f^{-1})=\{(f(x),x):f(x)\in B\}\text{.}$$
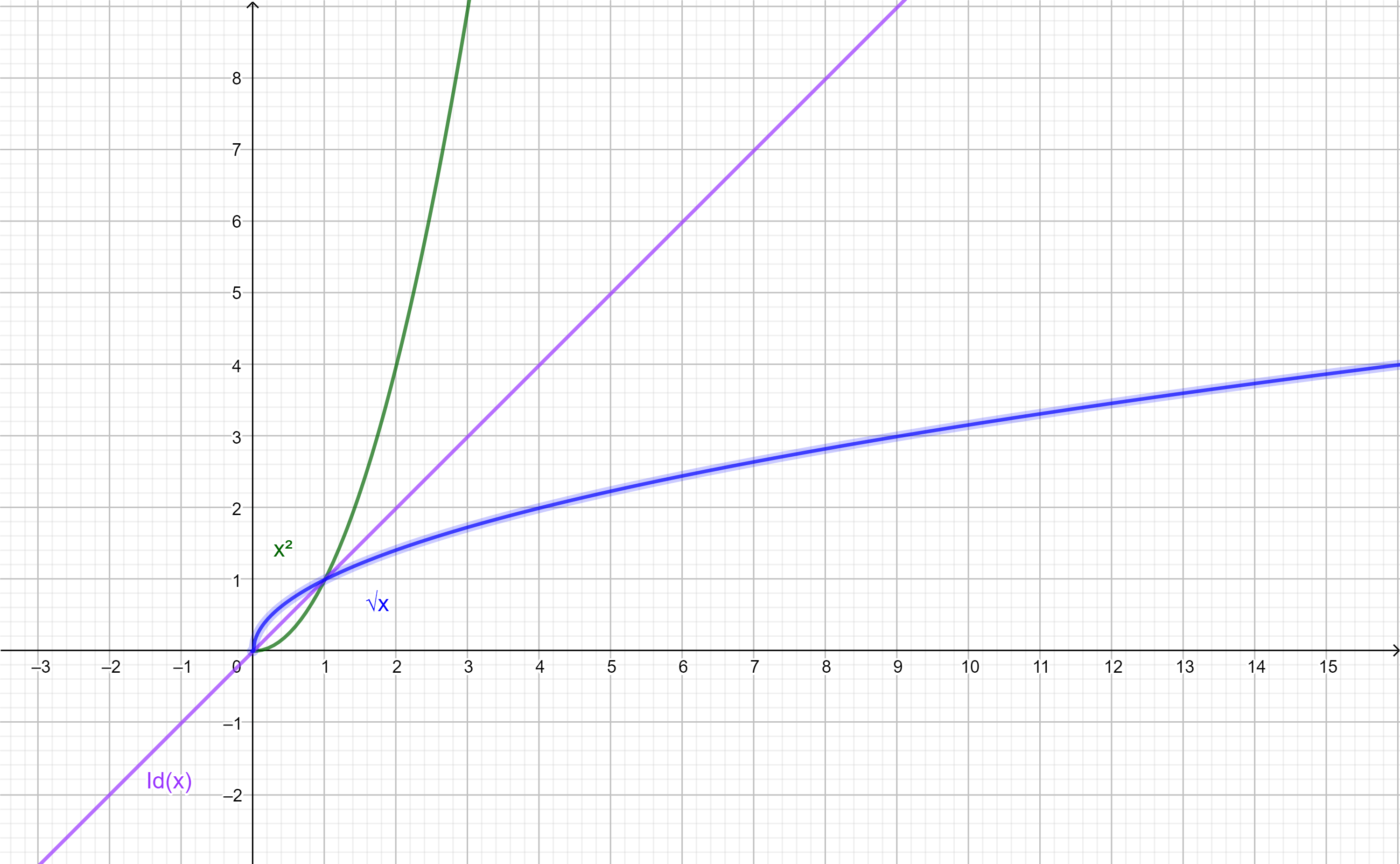
Esto nos permite observar que un punto $(y,x)\in Graf(f^{-1})$ es la reflexión ortogonal del punto $(x,y)\in Graf(f)$ respecto a la función identidad.

De este modo podemos obtener la gráfica de $f^{-1}$ reflejando ortogonalmente la gráfica de $f$ respecto a la identidad.

En este ejemplo tomamos la función $f(x)=x^2$ en el dominio donde cumple ser biyectiva por lo que su función inversa sería $h(x)=\sqrt{x}$:

En la sección de Tarea moral encontrarás algunos ejercicios que te ayudarán a poner en práctica lo desarrollado en esta entrada.

Más adelante

En la siguiente entrada, comenzaremos a revisar el conjunto de las funciones trigonométricas. Veremos sus definiciones, algunas identidades trigonométricas que serán de utilidad y sus gráficas.

Tarea moral

Realiza las gráficas de las siguientes funciones dado que $f(x)=x^3$:

• $f(x)+4$
• $f(x-3)+2$
• $f^{-1}(x)$
• $f(2x)$
• $2f(x)$

Entradas relacionadas

• Ir a: Cálculo Diferencial e Integral I
• Entrada anterior del curso: Cálculo Diferencial e Integral I: Funciones crecientes y decrecientes. Funciones acotadas.
• Entrada siguiente del curso: Cálculo Diferencial e Integral I: Funciones trigonométricas. (Primera parte)
• Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»