(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Alguna vez te haz preguntado: ¿qué ocurre con un cociente de cocientes? Comencemos con un ejemplo para crear intuición.

Digamos que queremos que el siguiente cociente tenga sentido:
\begin{align*}
(G/K) \Big/ (H/T).
\end{align*}
Para ello, necesitamos que $K\unlhd G$, $T\unlhd H$ y además $H/T \unlhd G/K$. Lo último nos indica en particular que $H/T$ debe ser un subconjunto de $ G/K$. Como los elementos de $H/T$ son de la forma $hT$con $h\in H$ y los de $G/K$ de la forma $gK$ con $g\in G$, para que $H/T\subseteq G/K$ necesitamos primero que las clases se formen con respecto al mismo subgrupo, es decir requerimos que $T=K$. Además, todo $h\in H$ debería ser elemento de $G$, por lo que $H\subseteq G.$

Volvamos a escribir el cociente ahora con $T=K$,
\begin{align*}
(G/K) \Big/ (H/K).
\end{align*}
También actualicemos las necesidades:

1. $K\unlhd G$,
2. $K\unlhd H$ y
3. $H/K\unlhd G/K$ con $H\subseteq G.$

Notemos que $K \subseteq H \subseteq G$ y la primera condición, $K \unlhd G$, nos da la segunda, $K\unlhd H$. También podemos pedir que $H\unlhd G$ y de esto obtendríamos la tercera necesidad, $H/K\unlhd G/K$. Además, al pedir que $H\unlhd G$ podríamos considerar al cociente $G/H$.

En esta entrada, demostraremos el Tercer Teorema de Isomorfía, el cual nos respalda en afirmar, bajo las condiciones ya establecidas, que
\begin{align*}
G/H \cong (G/K) \Big/ (H/K).
\end{align*}

De esto podemos concluir que, cuando se tiene un cocientes de cocientes existe una manera de reducirlo ya que es isomorfo a un cociente más sencillo.

Enunciado del Teorema

Comenzaremos enunciando y demostrando el teorema. Como ya dijimos en la entrada del Primer Teorema de Isomorfía, aquí volveremos a usarlo para probar el Tercero.

Teorema. (Tercer Teorema de Isomorfía)
Sean $G$ un grupo, $H$ y $K$ subgrupos normales de $G$ con $K\leq H$. Entonces $H/K \unlhd G/K$ y
\begin{align*}
(G/K)\, \Big/\, (H/K) \cong G/H.
\end{align*}

Demostración.
Sean $G$ un grupo, $H\unlhd G$, $K\unlhd G$ con $K \leq H$.
Como $K\unlhd G$, al conjugar elementos de $K$ con cualquier elemento de $G,$ obtenemos elementos de $K$. En particular, si conjugamos elementos de $K$ con cualquier elemento de $H,$ obtenemos elementos de $K$. Así obtenemos que $K\unlhd H$.

Ahora, usaremos el Primer Teorema de Isomorfía para probar el isomorfismo buscado, para ello bastaría definir una $\varphi$ tal que $\text{Núc } \varphi = H/K$ y $\text{Im }\varphi = G/H$.

Sea $\varphi: G/K \to G/H$ con $\varphi(gK) = gH$ para toda $g\in G$.

Primero, veamos que $\varphi$ está bien definida.
Tomemos $a,b \in G$.
\begin{align*}
aK = bK &\Rightarrow b^{-1}a \in K \\
&\Rightarrow b^{-1}a\in H &\text{Porque } K \subseteq H\\
&\Rightarrow aH = bH.
\end{align*}
Esto nos dice que debido a la contención $K\subseteq H$, dos clases que son iguales con respecto a $K$, seguirán siendo iguales con respecto a $H$. Así, $\varphi$ está bien definida.

Ahora veamos que $\varphi$ es un homomorfismo. Sean $a,b\in G$
\begin{align*}
\varphi(aKbK) = \varphi(abK) = ab H = aHbH = \varphi(aK)\varphi(bK)
\end{align*}
entonces $\varphi$ es un homomorfismo.

Ahora sí, comencemos a analizar su núcleo:
\begin{align*}
\text{Núc }\varphi &= \{gK\in G/K \,:\, \varphi(gK) = e_{G/H}\} & \text{Definición de núcleo} \\ &= \{gK\in G/K \,:\, gH = H \} &\text{Definición de $\varphi$ y neutro del cociente}\\
&= \{gK \in G/K \,:\, g\in H\} & gH = H \Leftrightarrow g\in H \\
&= H/K
\end{align*}

Así, $\text{Núc }\varphi =H/K$ y en consecuencia $H/K \unlhd G/K.$

Veamos ahora que $\varphi$ es suprayectiva.
Sea $x\in G/H$, $x = gH$ con $g\in G$. Por definición de $\varphi$ tenemos,
\begin{align*}
x = gH = \varphi(gK) \in \text{Im }\varphi.
\end{align*}
Como siempre sucede que $\text{Im }\varphi \subseteq G/H$. Entonces $\text{Im }\varphi = G/H$.

Por el Primer Teorema de Isomorfía:
\begin{align*}
(G/K)\,\Big/\, \text{Núc }\varphi \cong \text{Im }\varphi
\end{align*}
entonces, de acuerdo a lo que analizamos,
\begin{align*}
(G/K)\,\Big/\, (H/K) \cong G/H.
\end{align*}

$\blacksquare$

Ejemplo

Veamos ahora un ejemplo del Tercer Teorema de Isomorfía.

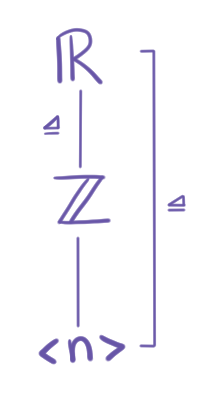
Tomemos $G = (\r, +), H= (\z, +)$. Consideremos $n\in\z$ y $K = \left< n\right> = n\z$.

Sabemos que $\z\unlhd\r$ y que $\left< n\right>\unlhd \r$ ya que $\r$ es abeliano.
Por el 3er Teorema de Isomorfía,
\begin{align*}
(\r/\left<n\right>)\,\Big/\, (\z/\left< n\right>) \cong \r/\z.
\end{align*}

Veamos cómo es $\z / \left<n\right>$. Sea $\varphi:\z\to\z_n$ con $\varphi(m) = \bar{m}$ para todo $m\in\z$. Por lo que tenemos estudiado de Álgebra Superior II, sabemos que $\varphi$ es un epimorfismo con $\text{Núc }\varphi = \left<n\right>$ y por el 1er Teorema de Isomorfía
\begin{align*}
\z/\left<n\right> \cong \z_n.
\end{align*}

Analicemos ahora el cociente $\r/\left<n\right>$. Sea $\psi:\r \to \mathbb{C}^*$ con $\psi(x) = e^{\frac{2\pi ix}{n}}$ para toda $x\in \r$. Tenemos que $\psi$ es un homomorfismo con
\begin{align*}
\text{Núc }\psi &= \{x\in \r : \psi(x) = 1\} = \{x\in\r : e^{\frac{2\pi ix}{n}} = 1\}\\
&= \{nk : k\in\z\} = \left< n\right>.\\
\text{Im }\psi &= \{\psi(x) : x\in \r\} = \{e^{\frac{2\pi ix}{n}}: x\in \r\}\\
&=\{z \in \mathbb{C}:|z|=1\} = \s^1.
\end{align*}
Por el 1er Teorema de Isomorfía aplicado a $\psi$ obtenemos que $\r/\left<n\right> \cong \s^1$.

Por último, veamos cómo es $\r/\z$. Sea $F:\r\to\mathbb{C}^*$ con $F(x) = e^{2\pi ix}$ para toda $x\in\r$. Tenemos que $F$ es un homomorfismo con
\begin{align*}
\text{Núc }F &= \{x\in\r : F(x) = 1\} = \{x\in\r : e^{2\pi ix} = 1\}\\
&= \{x : x\in\z\} = \z\\
\text{Im }F &= \{F(x) : x\in\r\} = \{e^{2\pi ix}: x\in \r\}\\
&= \{z\in\mathbb{C} : |z| = 1\} = \s^1.
\end{align*}

Así, $\r/\z \cong \s^1$ por el 1er Teorema de Isomorfía.

Recapitulando, hemos visto que
\begin{align*}
\s^1 &\cong \r/\left<n\right> \\
\z_n &\cong \z/\left<n\right>.
\end{align*}

Entonces, retomando el cociente con el que iniciamos:
\begin{align*}
(\r/\left<n\right>) \,\Big/\, (\z/\left<n\right>) \cong \r/\z \cong \s^1.
\end{align*}

donde $\s^1\cong \r/\left<n\right>$ y $\z_n\cong \z/\left<n\right>.$ Entonces, un cociente de $\s^1$ módulo un subgrupo suyo no trivial (que es isomorfo a $\z_n$), resulta ser isomorfo a $\s^1$.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Sea $G$ un grupo, $H$ y $K$ subgrupos normales de $G$ con $K$ un subgrupo de $H$. Describe cómo son en general los elementos del cociente $(G/K)/(H/K)$.
2. Sea $\z_{12}$, considera sus subgrupos $H = \langle\bar{2}\rangle$ y $K = \langle\bar{4}\rangle$.
   • Determina en este caso qué pasa al aplicar el Tercer Teorema de Isomorfía.
   • Describe cómo son los cocientes $\z_{12}/K$ y $H/K$ encontrando explícitamente su orden, el orden de sus elementos y su tabla de multiplicar.

Más adelante…

Ya vamos 3/4 de los teoremas. ¡Qué emoción! En la próxima entrada veremos el más largo de los Teoremas de Isomorfía.

Entradas relacionadas

• Ir a Álgebra Moderna I.
• Entrada anterior del curso: Segundo Teorema de Isomorfía.
• Siguiente entrada del curso: Cuarto Teorema de Isomorfía.
• Resto de cursos: Cursos.